2. 同济大学 地下建筑与工程系,上海 200092
2. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
柱孔扩张理论由于形式简单,力学原理明确,因此在岩土工程领域得到广泛应用[1-4].然而,受理论及本构模型的限制,早期柱孔扩张解答多数假设土体为各向同性的理想弹塑性材料,且在解答过程中忽略竖向应力作用,仅考虑径向应力和环向应力来求解孔周土体的应力和位移[5-9].剑桥模型由于不仅可以综合考虑土体各应力之间的相互关系,同时可以体现土体剪切变形和剪切破坏的一致性,因此被广泛应用于柱孔弹塑性扩张研究中.如:Collins等[10-11]基于相似分析方法,采用原始剑桥模型和修正剑桥模型推导了初始应力各向同性土体中圆孔排水和不排水扩张问题的弹塑性解答;Yu[12]系统总结了初始应力各向同性土体中圆孔扩张问题的各类解答,并详细介绍了圆孔扩张理论在岩土工程中的应用;Cao等[13]、李镜培等[14]在初始应力各向同性假设的基础上,基于修正剑桥模型推导了圆孔扩张问题的半解析半数值解答;Chen等[15]基于修正剑桥模型,从严格的弹塑性本构关系出发,推导了K0固结土体中柱孔不排水扩张问题的数值解答,但其解答过程较为繁琐,不易推广和应用.可以看出,尽管目前基于剑桥模型的柱孔扩张解答考虑了柱孔扩张过程中各应力之间的相互关系,但其解答均没有考虑到K0固结特性对柱孔扩张过程中土体力学行为的影响,进而无法体现天然饱和黏土中柱孔弹塑性扩张的本质.
由于受沉积环境和固结环境的影响,天然状态下黏性土多处于K0固结状态.由于初始应力各向异性对土体的力学特性存在较大影响,因此实际工程中对应的圆孔扩张问题需考虑土体的K0固结特性.鉴于此,本文采用修正剑桥模型,在充分考虑土体K0固结特性和应力历史的基础上,推导了天然饱和黏土中柱孔不排水扩张问题的弹塑性解析解答,并在与Chen等[15]基于精确本构关系的数值解答对比验证的基础上,详细研究了土体初始应力各向异性对柱孔扩张过程的影响.
1 柱孔扩张力学模型如图 1所示,在内压力σa的作用下,初始半径为a0的柱孔在水平向应力和竖向应力分别为σh0和σv0的K0固结初始应力各向异性饱和黏土体中不排水扩张,随着内压力σa的不断增加,孔径从a0扩张至a,孔壁土体将首先发生屈服,由弹性状态进入塑性状态,进而在柱孔周围形成一定范围的塑性区.以au表示柱孔最终半径,以ry表示柱孔扩张过程中对应的塑性区半径,塑性区边界的径向位移以Ury表示.在整个求解过程中假定应力以压为正,且弹性区土体服从胡克定律和小变形假定,土体进入塑性后采用大变形理论和MCC模型来描述土体的力学特性.
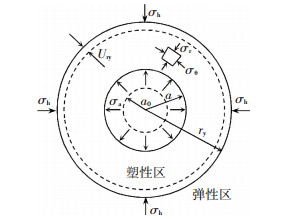
|
图 1 柱孔扩张力学模型 Figure 1 Mechanical model for cylindrical cavity expansion |
基于以上条件可知,对于初始应力各向异性天然饱和黏土,柱孔周围初始径向应力σ′r0、环向应力σ′θ0和竖向应力σ′z0之间存在如下关系:
| $ {{\sigma '}_{{\rm{r0}}}} + {{\sigma '}_{{\rm{\theta 0}}}} = {K_0}{{\sigma '}_{{\rm{z}}0}}, $ | (1) |
式中K0为土体静止侧压力系数,其大小反映了土体初始应力各向异性程度.
在柱孔不排水扩张的任何阶段,孔周土体中任一单元体都满足平衡方程:
| $ \frac{{\partial {\sigma _{\rm{r}}}}}{{\partial r}} + \frac{{{\sigma _{\rm{r}}} - {\sigma _{\rm{\theta }}}}}{r} = 0. $ | (2) |
由弹性应力、应变和位移之间的相互关系,并考虑土体初始水平向应力σh0和初始竖向应力σv0之间的关系,可得弹性区位移解答[13]:
| $ {U_{\rm{r}}} = \frac{{\left( {{\sigma _{\rm{a}}} - {\sigma _{{\rm{h0}}}}} \right)}}{{2G}}{\left( {\frac{a}{r}} \right)^2}r, $ | (3) |
式中:G=3(1-2ν′)υp′/[2(1+ν′)κ]为土体的剪切模量, κ为卸荷曲线在υ-ln p′平面上的斜率, υ=1+e为土体比体积, e为土体孔隙比, p′=σ′ⅱ/3为平均有效主应力, ν'为土体有效泊松比.
进而,由胡克定律和小变形关系可得孔周弹性区应力分量σr,σθ和σz的表达式[13]:
| $ {\sigma _{\rm{r}}} = {\sigma _{{\rm{h0}}}} + \left( {{\sigma _{\rm{a}}} - {\sigma _{{\rm{h0}}}}} \right){\left( {\frac{a}{r}} \right)^2}, $ | (4) |
| $ {\sigma _{\rm{\theta }}} = {\sigma _{{\rm{h0}}}} - \left( {{\sigma _{\rm{a}}} - {\sigma _{{\rm{h0}}}}} \right){\left( {\frac{a}{r}} \right)^2}, $ | (5) |
| $ {\sigma _{\rm{z}}} = {\sigma _{{\rm{v0}}}}. $ | (6) |
在柱孔不排水扩张条件下,土体体积不发生变化,因此,弹性区土体体应变可表示为
| $ {\rm{d}}v = - \kappa \frac{{{\rm{d}}p'}}{{p'}} = 0. $ | (7) |
由式 (7) 可知,在扩孔过程中弹性区平均有效主应力p′保持不变,且由式 (4)~(6) 可知弹性区平均总主应力p亦保持不变,则根据有效应力原理可得弹性区超孔隙水压力为零,即:
| $ u = {u_0}, $ | (8) |
式中u0为初始孔隙水压力.
2.2 弹塑性边界随着扩张内压力的不断增加,孔壁处土体首先屈服进入塑性状态.文献[15]根据屈服面之间的几何关系,给出了可以考虑土体K0固结特性的修正剑桥模型,其屈服准则可表示为[15]
| $ q = M\sqrt {p'\left[ {{{p'}_{\rm{c}}}\left( {1 + {{\left( {{\eta _0}/M} \right)}^2}} \right) - p'} \right]} . $ | (9) |
式中:η0=|3(1-K0)|/(2K0+1) 为初始应力比,p′c为土体前期平均有效固结应力, M为p′-q平面中CSL线的斜率,其值等于6sin φ′/(3-sin φ′),φ′为土体有效内摩擦角, q为广义剪应力,可表示为:
| $ q = \sqrt {\frac{3}{2}{s_{{\rm{ij}}}}{s_{{\rm{ij}}}}} , $ | (10) |
| $ {s_{{\rm{ij}}}} = {\sigma _{{\rm{ij}}}} - p{\delta _{{\rm{ij}}}}. $ | (11) |
式中sij为偏应力张量,δij为克朗内克符号.
由于柱孔扩张过程中其周围弹性区平均有效主应力p′保持不变,故弹塑性边界处土体平均有效主应力p′y仍保持不变,即:
| $ {{p'}_{\rm{y}}} = {{p'}_0}. $ | (12) |
由式 (12) 可知,柱孔弹性扩张阶段孔周土体单元在p′-q平面上有效应力路径从初始应力点 (p′0, q0) 开始,竖直上升与初始屈服面相交于 (p′0, qy) 点,由式 (9) 和式 (12) 可得弹塑性边界处的广义偏应力qy为
| $ {q_{\rm{y}}} = M{{p'}_0}\sqrt {{\rm{OCR}}\left( {1 + \frac{{\eta _0^2}}{{{M^2}}}} \right) - 1} . $ | (13) |
式中OCR=p′c/p′0,为土体超固结比.
在弹塑性边界处,弹性解答仍然成立,故由式 (4)~(6) 和式 (8) 可得弹塑性边界处应力分量σry,σθy和σzy之间存在如下关系:
| $ {{\sigma }_{\text{ry}}}+{{\sigma }_{\text{ }\text{ }\!\!\theta\!\!\text{ }\text{ y}}}={{\sigma }_{\text{r0}}}+{{\sigma }_{\text{ }\theta \text{ 0}}}=2{{\sigma }_{\text{h0}}}, $ | (14) |
| $ {\sigma _{{\rm{zy}}}} = {\sigma _{{\rm{z0}}}}. $ | (15) |
由式 (10) 可知,弹塑性边界处的广义偏应力qy同样可表示为
| $ {q_{\rm{y}}} = \sqrt {\frac{3}{2}\left( {{{\sigma '}_{{\rm{ijy}}}} - p'{\delta _{{\rm{ij}}}}} \right)\left( {{{\sigma '}_{{\rm{ijy}}}} - p'{\delta _{{\rm{ij}}}}} \right)} , $ | (16) |
式中σ′ijy为弹塑性边界处的应力张量.
联立式 (14)~(16) 可解得:
| $ {{\sigma '}_{{\rm{ry}}}} = {{\sigma '}_{{\rm{r0}}}} + \frac{1}{{\sqrt 3 }}\sqrt {q_{\rm{y}}^2 - {{\left( {{\eta _0}{{p'}_0}} \right)}^2}} , $ | (17) |
| $ {{{\sigma }'}_{\text{ }\!\!\theta\!\!\text{ y}}}={{{\sigma }'}_{\text{r0}}}-\frac{1}{\sqrt{3}}\sqrt{q_{\text{y}}^{2}-{{\left( {{\eta }_{0}}{{{{p}'}}_{0}} \right)}^{2}}}, $ | (18) |
| $ {{\sigma '}_{{\rm{zy}}}} = {{\sigma '}_{{\rm{z0}}}}. $ | (19) |
将式 (17) 代入式 (3) 可得弹塑性边界处的位移:
| $ {U_{{\rm{ry}}}} = \frac{{\sqrt {q_{\rm{y}}^2 - {{\left( {{\eta _0}{{p'}_0}} \right)}^2}} }}{{2\sqrt 3 G}}{r_{\rm{y}}}. $ | (20) |
由于半无限体中柱孔扩张为平面应变问题,故柱孔扩张过程中不产生竖向应变εz,即:
| $ {\varepsilon _{\rm{z}}} = 0. $ | (21) |
在不排水条件下,体应变εv=0,故轴向应变εr和环向应变εθ之间存在如下关系:
| $ {\varepsilon _{\rm{r}}} = - {\varepsilon _{\rm{\theta }}}. $ | (22) |
为考虑桩周土体进入塑性状态后的大变形效应,采用对数应变将柱孔周围塑性区内土体应变分量表示为:
| $ {\varepsilon _{\rm{r}}} = - \ln \left( {\frac{{{\rm{d}}r}}{{{\rm{d}}{r_0}}}} \right), $ | (23) |
| $ {{\varepsilon }_{\text{ }\!\!\theta\!\!\text{ }}}=-\ln \left( \frac{r}{{{r}_{0}}} \right). $ | (24) |
将式 (21) 和式 (22) 代入式 (24),在塑性区内积分,并考虑孔壁的初始条件和弹塑性边界条件可得:
| $ r_{\rm{y}}^2 - r_{{\rm{y0}}}^2 = {a^2} - a_0^2, $ | (25) |
式中ry0为ry对应的初始半径位置.
考虑到在不排水条件下土体体积守恒,故弹塑性边界处位移Ury=ry-ry0,则式 (25) 可进一步表示为
| $ r_{\rm{y}}^2 - {\left( {{r_{\rm{y}}} - {U_{{\rm{ry}}}}} \right)^2} = {a^2} - a_0^2. $ | (26) |
将式 (20) 代入式 (26),并忽略式中
| $ {\left( {\frac{{{r_{\rm{y}}}}}{a}} \right)^2} = \frac{{\sqrt 3 G}}{{\sqrt {q_{\rm{y}}^2 - {{\left( {{\eta _0}{{p'}_0}} \right)}^2}} }}\left[ {1 - {{\left( {\frac{{{a_0}}}{a}} \right)}^2}} \right]. $ | (27) |
对于MCC模型,土体屈服后体应变增量dεv由弹性体应变增量dεve和塑性体应变dεvp两部分组成,且由于不排水条件下体积守恒,上述关系可表示为
| $ \kappa \frac{{{\rm{d}}p'}}{{\nu p'}} + \left( {\lambda - \kappa } \right)\frac{{{\rm{d}}{{p'}_c}}}{{\nu {{p'}_c}}} = 0, $ | (28) |
式中λ为各向同性加载曲线在υ-ln p′平面上的斜率.
对式 (28) 在塑性区内积分,并考虑到弹塑性边界处p′c=p′c0,p′=p′0,则可得:
| $ {{p'}_{\rm{c}}} = p'{\rm{OCR}}{\left( {\frac{{p'}}{{{{p'}_0}}}} \right)^{\frac{{ - \lambda }}{{\lambda - \kappa }}}}. $ | (29) |
将式 (9) 代入式 (29) 可得:
| $ q = p'\sqrt {\left( {{M^2} + \eta _0^2} \right){\rm{OCR}}{{\left( {\frac{{p'}}{{{{p'}_0}}}} \right)}^{ - \frac{1}{\mathit{\Lambda }}}} - {M^2}} , $ | (30) |
式中Λ=1-κ/λ为塑性体应变比.
由MCC模型对应的临界状态条件η=M,根据式 (30) 可求得孔周围土体单元进入临界状态时对应的平均有效主应力p′f和偏应力qf分别为:
| $ {{p'}_{\rm{f}}} = {{p'}_0}{\left[ {\frac{{\left( {{M^2} + \eta _0^2} \right){\rm{OCR}}}}{{2{M^2}}}} \right]^\mathit{\Lambda }}, $ | (31) |
| $ {q_{\rm{f}}} = M{{p'}_0}{\left[ {\frac{{\left( {{M^2} + \eta _0^2} \right){\rm{OCR}}}}{{2{M^2}}}} \right]^\mathit{\Lambda }}. $ | (32) |
由于平衡微分方程式 (2) 在塑性区仍成立,故柱孔扩张后孔周塑性区内任意位置处总应力σrx可通过积分式 (2) 得到:
| $ {\sigma _{{\rm{rx}}}} = {\sigma _{{\rm{ry}}}} - \int_{{r_{\rm{y}}}}^{{r_{\rm{x}}}} {\frac{{\left( {{\sigma _{\rm{r}}} - {\sigma _{\rm{\theta }}}} \right)}}{r}} {\rm{d}}r, $ | (33) |
式中 (σr-σθ) 与计算点的位置rx有关,因此,式 (33) 无法直接积分得出解析表达式.然而,在孔周塑性区内广义偏应力q基本为一定值,且孔周临界状态区内土体单元径向应力σ′rf,环向应力σ′θf与竖向应力σ′zf之间存在如下关系[15]:
| $ {{\sigma '}_{{\rm{zf}}}} = \frac{{{{\sigma '}_{{\rm{rf}}}} + {{\sigma '}_{{\rm{\theta f}}}}}}{2}. $ | (34) |
基于上述关系,如图 2所示,假设式 (34) 在整个塑性区内均成立,使 (σr-σθ) 独立于计算点的位置rx,则塑性区半径ry可重新表示为
| $ {\left( {\frac{{{r_{\rm{y}}}}}{a}} \right)^2} = \frac{{\sqrt 3 G}}{{\sqrt {q_{\rm{y}}^2 - {{\left( {{\eta _0}{{p'}_0}} \right)}^2}} }}\left[ {1 - {{\left( {\frac{{{a_0}}}{a}} \right)}^2}} \right]. $ | (35) |
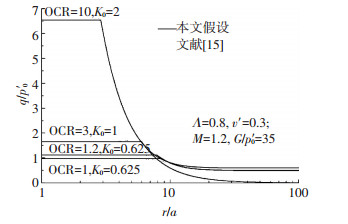
|
图 2 孔周假设偏应力分布与实际情况对比 Figure 2 Comparisons of derivative stress distributions around cavity between assumed and actual cases |
同时,基于上述假设,式 (34) 可进一步表示为
| $ {\sigma _{{\rm{rx}}}} = {\sigma _{{\rm{ry}}}} - \frac{{2{q_{\rm{f}}}}}{{\sqrt 3 }}\int_{{r_{\rm{y}}}}^{{r_{\rm{x}}}} {\frac{1}{r}{\rm{d}}r} . $ | (36) |
将式 (35) 代入式 (36),并在塑性区内积分可得孔周塑性区内径向总应力为
| $ {\sigma _{{\rm{rx}}}} = {\sigma _{{\rm{h0}}}} + \frac{{\bar q}}{{\sqrt 3 }} + \frac{{{q_{\rm{f}}}}}{{\sqrt 3 }}\ln \frac{{\sqrt 3 G}}{{\bar q}}\left( {\frac{{{a^2} - a_0^2}}{{r_{\rm{x}}^2}}} \right), $ | (37) |
式中q=
将式 (34) 和式 (37) 代人式 (32),可得塑性区环向总应力和竖向总应力的解析式:
| $ {{\sigma }_{\text{ }\!\!\theta\!\!\text{ x}}}={{\sigma }_{\text{h0}}}+\frac{{\bar{q}}}{\sqrt{3}}+\frac{{{q}_{\text{f}}}}{\sqrt{3}}\left[ \ln \frac{\sqrt{3}G}{{\bar{q}}}\left( \frac{{{a}^{2}}-a_{0}^{2}}{r_{\text{x}}^{2}} \right)-2 \right], $ | (38) |
| $ {\sigma _{{\rm{zx}}}} = {\sigma _{{\rm{h0}}}} + \frac{{\bar q}}{{\sqrt 3 }} + \frac{{{q_{\rm{f}}}}}{{\sqrt 3 }}\left[ {\ln \frac{{\sqrt 3 G}}{{\bar q}}\left( {\frac{{{a^2} - a_0^2}}{{r_{\rm{x}}^2}}} \right) - 1} \right]. $ | (39) |
根据有效应力原理,结合式 (37)~(39) 和式 (31),可得塑性区内任意位置处的超孔隙水压力Δurx为
| $ \begin{array}{l} \Delta {u_{{\rm{rx}}}} = \frac{{\left( {{K_0} - 1} \right){{p'}_0}}}{{1 + 2{K_0}}} + \frac{{{q_{\rm{f}}}}}{{\sqrt 3 }}\ln \frac{{\sqrt 3 G}}{{\bar q}}\left( {\frac{{{a^2} - a_0^2}}{{r_{\rm{x}}^2}}} \right) + \\ \;\;\;\;\;\;\;\;\frac{{\bar q - {q_{\rm{f}}}}}{{\sqrt 3 }} + {{p'}_0}\left[ {1 - {{\left[ {\frac{{\left( {{M^2} + \eta _0^2} \right){\rm{OCR}}}}{{2{M^2}}}} \right]}^\mathit{\Lambda }}} \right]. \end{array} $ | (40) |
令式 (37) 和式 (40) 中rx=a,可得孔壁处的扩孔压力σa和孔壁处的超孔隙水压力Δua:
| $ {\sigma _{\rm{a}}} = {\sigma _{{\rm{h0}}}} + \frac{{\bar q}}{{\sqrt 3 }} + \frac{{{q_{\rm{f}}}}}{{\sqrt 3 }}\ln \frac{{\sqrt 3 G}}{{\bar q}}\left( {1 - \frac{{a_0^2}}{{{a^2}}}} \right), $ | (41) |
| $ \begin{array}{l} \Delta {u_{\rm{a}}} = \frac{{\left( {{K_0} - 1} \right){{p'}_0}}}{{1 + 2{K_0}}} + \frac{{{q_{\rm{f}}}}}{{\sqrt 3 }}\ln \frac{{\sqrt 3 G}}{{\bar q}}\left( {1 - \frac{{a_0^2}}{{{a^2}}}} \right) + \\ \;\;\;\;\;\;\;\;\frac{{\bar q - {q_{\rm{f}}}}}{{\sqrt 3 }} + {{p'}_0}\left[ {1 - {{\left[ {\frac{{\left( {{M^2} + \eta _0^2} \right){\rm{OCR}}}}{{2{M^2}}}} \right]}^\mathit{\Lambda }}} \right]. \end{array} $ | (42) |
当a/a0→∞时,从式 (41) 和式 (42) 可得孔壁极限扩孔压力σrult和孔壁处的极限超孔隙水压力Δuault:
| $ \begin{array}{l} \Delta {u_{{\rm{ault}}}}:\\ \;\;\;\;\;\;\;\;\;{\sigma _{{\rm{rult}}}} = {\sigma _{{\rm{h0}}}} + \frac{{\bar q}}{{\sqrt 3 }} + \frac{{{q_{\rm{f}}}}}{{\sqrt 3 }}\left( {\ln \frac{{\sqrt 3 G}}{{\bar q}} + 1} \right), \end{array} $ | (43) |
| $ \begin{array}{l} \Delta {u_{{\rm{ault}}}} = \frac{{\left( {{K_0} - 1} \right){{p'}_0}}}{{1 + 2{K_0}}} + \frac{{{q_{\rm{f}}}}}{{\sqrt 3 }}\ln \frac{{\sqrt 3 G}}{{\bar q}} + \frac{{\bar q - {q_{\rm{f}}}}}{{\sqrt 3 }} + \\ \;\;\;\;\;\;\;\;\;\;{{p'}_0}\left[ {1 - {{\left[ {\frac{{\left( {{M^2} + \eta _0^2} \right){\rm{OCR}}}}{{2{M^2}}}} \right]}^\mathit{\Lambda }}} \right]. \end{array} $ | (44) |
值得注意的是:若令式 (37)~(44) 中K0=1,则土体为各向同性体,本文解答可退化为各向同性体中柱孔不排水扩张解答,与文献[13]所得出的各向同性土体中柱孔扩张解答完全一致,说明文献[13]的解答是本文解答的一个特例.
3 验证与分析为验证本文所得解答的正确性和合理性,同时为分析K0固结特性和应力历史对柱孔扩张过程的影响,本文选取不同K0固结条件下的3种饱和黏土进行分析,其土体参数取值均引自文献[15],具体数值见表 1.
此外,根据文献[15],4种土体临界状态线CSL斜率M=1.2,初始K0固结曲线斜率λ=0.15,回弹曲线的斜率κ=0.03,泊松比ν=0.278.
3.1 对比验证图 3(a)~(c)为本文解析解与文献[15]所得不同初始应力各向异性土体中柱孔不排水扩张后孔周土体应力分布的对比,图中横坐标轴均为对数坐标.
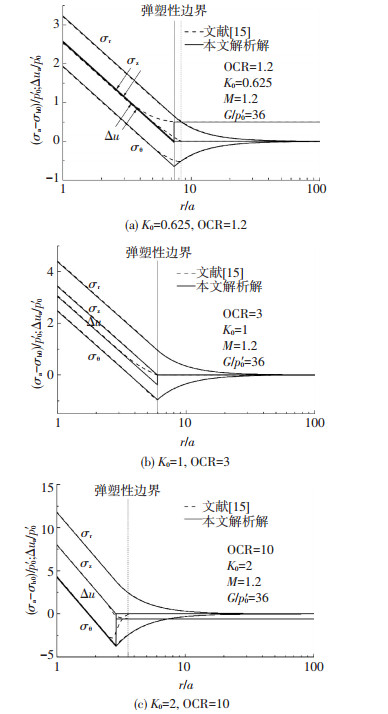
|
图 3 孔壁周围应力分布解析解与数值解对比 Figure 3 Comparisons of stress distributions around cavity between numerical solution and analytical solution |
从图 3可见,本文解析解答与基于严格本构关系的数值解在靠近孔壁的塑性区内吻合良好,仅在远离孔壁的弹塑性边界处两者存在一些差异.然而,对于静压沉桩和静力触探等岩土工程问题,多关注靠近孔壁处的应力分布,因此本文解答可以满足一般工程问题的需要.
同时,从图 3可见,初始应力各向异性饱和黏土中柱孔不排水扩张引起孔壁周围土体应力状态发生较大变化,且随距孔壁距离的增加,土体应力变化逐渐减小,在弹性区内趋于初始应力状态.
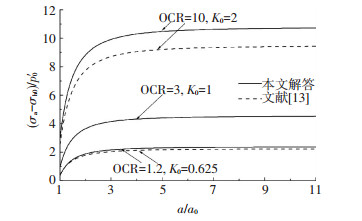
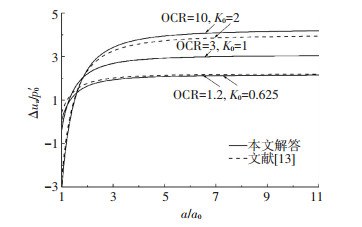
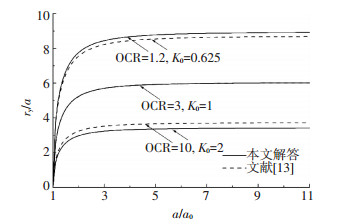
3.2 柱孔扩张过程分析图 4~6分别给出了初始应力各向异性黏土中柱孔不排水扩张过程中孔壁压力σa、孔壁超孔压Δua及塑性区半径ry随当前孔径a的变化规律,图中变量均采用无量纲化形式表示.
|
图 4 柱孔扩张过程中孔壁应力变化 Figure 4 Variations of cavity stresses during cavity expansion |
|
图 5 柱孔扩张过程中孔壁超孔隙水压力变化 Figure 5 Variations of excess pore water pressures at cavity wall during cavity expansion |
|
图 6 柱孔扩张过程中塑性区半径变化 Figure 6 Variations of plastic radius during cavity expansion |
从图 4可见,孔壁压力σa在柱孔扩张初期 (a/a0 < 2) 迅速增大,之后 (a/a0≥2) 孔壁压力σa增长缓慢且逐步趋于临界状态,当a/a0≥5时,孔壁压力趋于稳定,土体进入临界状态.
从图 5可知,与孔壁压力σa相对应,孔壁处的超孔压在柱孔扩张初期随孔径的增大而迅速增大,此后逐步趋向于恒定值.值得注意的是,对于超固结土 (OCR>1), 在柱孔扩张初期孔壁处首先产生负超孔压,之后随孔径的增大,超孔压由负值转变为正值,且逐步趋向于临界值,这一现象与文献[13, 15]分析所得规律一致.
从图 6可看出,塑性区半径ry在柱孔扩张过程中随孔径a的变化规律与孔壁压力σa和孔壁超孔隙水压力Δua随孔径的变化规律一致,均是在扩孔初期变化较大,之后逐步趋于定值.
除以上规律外,图 4~6亦给出了基于各向同性假设的解答[13]和本文考虑初始应力各向异性解答之间的差异.可以看出,初始应力各向异性和应力历史对柱孔扩张过程有明显的影响,特别是对柱孔扩张过程中极限扩张压力的影响最为明显.
4 结论本文针对K0固结初始应力各向异性土体中柱孔不排水扩张问题,采用修正剑桥模型在考虑土体K0固结特性和应力历史的基础上,推导了柱孔不排水扩张的弹塑性解析解.在与既有基于严格本构关系的数值解对比验证的基础上,分析了K0固结特性及应力历史对柱孔扩张的影响,得出如下结论:
1)K0固结黏土中柱孔不排水扩张引起孔壁周围土体应力状态发生较大变化,且孔周应力随距径向距离的增加呈对数规律衰减,在弹性区逐渐趋向于初始应力状态.
2) 孔壁压力、超孔隙水压力和塑性区半径在柱孔不排水扩张的初始阶段变化较大,之后随孔径的增大而逐步趋向于临界状态.
3) 土体初始应力各向异性对孔壁压力、超孔隙水压力及塑性区半径存在一定程度的影响,特别对极限扩张压力存在较大影响,且其影响程度随土体各向异性的增加而增大.
| [1] | VESIC A S. Expansion of cavity in infinite soil mass[J]. Journal of Soil Mechanics Foundation Division, American Society of Civil Engineering, 1972, 98(3): 265-289. |
| [2] | RANDOLPH M F, CARTER J P, WROTH C P. Driven piles in clay-the effects of installation and subsequent consolidation[J]. Géotechnique, 1979, 29(4): 361-393. DOI: 10.1680/geot.1979.29.4.361 |
| [3] | SAGASET A C. Analysis of undrained soil deformation due to ground loss[J]. Géotechnique, 1987, 37(3): 301-320. DOI: 10.1680/geot.1987.37.3.301 |
| [4] | SAGASET A C. Prediction of ground movements due to pile-driving in clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(1): 55-66. DOI: 10.1061/(ASCE)1090-0241(2001)127:1(55) |
| [5] | RANDOLPH M F. Science and empiricism in pile foundation design[J]. Géotechnique, 2003, 53(10): 847-875. DOI: 10.1680/geot.2003.53.10.847 |
| [6] | HILL R. The mathematical theory of plasticity[M]. London: Oxford University Press, 1950. |
| [7] | CHADWICK P. The quasi-static expansion of spherical cavity in metals and ideal soils[J]. Quarterly Journal of Mechanics and Applied Mathematics, 1959, 12: 52-71. DOI: 10.1093/qjmam/12.1.52 |
| [8] | CATER J P, RANDOLPH M F, WROTH C P. Stress and pore pressure changes in clay during and after the expansion of a cylindrical cavity[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1979, 3(4): 305-322. DOI: 10.1002/(ISSN)1096-9853 |
| [9] | YU H S, HOULSBY G T. Finite cavity expansion in dilatants soils: loading analysis[J]. Géotechnique, 1991, 41(2): 173-183. DOI: 10.1680/geot.1991.41.2.173 |
| [10] | COLLINS I F, STIMPSON J R. Similarity solutions for drained and undrained cavity expansions in soils[J]. Géotechnique, 1994, 44(1): 21-34. DOI: 10.1680/geot.1994.44.1.21 |
| [11] | COLLINS I F, YU H S. Undrained cavity expansions in critical state soils[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1996, 20(7): 489-516. DOI: 10.1002/(ISSN)1096-9853 |
| [12] | YU H S. Cavity expansion methods in geomechanics[M]. Kluwer Academic Publishers: 2000. |
| [13] | CAO L F, TEH C I, CHANG M F. Undrained cavity expansion in modified Cam Clay Ⅰ: theoretical analysis[J]. Géotechnique, 2001, 51(4): 323-334. DOI: 10.1680/geot.2001.51.4.323 |
| [14] |
李镜培, 唐剑华, 张亚国, 等. 饱和粘土中球孔扩张问题弹塑性解析[J].
哈尔滨工业大学学报, 2014, 46(12): 71-77.
LI Jingpei, TANG Jianhua, ZHANG Yaguo, et al. elastic-plastic solution of sphere cavity expansion in saturated clay[J]. Journal of Harbin institute of technology, 2014, 46(12): 71-77. DOI: 10.11918/j.issn.0367-6234.2014.12.012 |
| [15] | CHEN S L, ABOUSLEIMAN Y N. Exact undrained elasto-plastic solution for cylindrical cavity expansion in modified Cam Clay soil[J]. Géotechnique, 2012, 62(5): 447-456. DOI: 10.1680/geot.11.P.027 |
 2017, Vol. 49
2017, Vol. 49


