2. 水力学与山区河流开发保护国家重点实验室 (四川大学),成都 610065;
3. 四川省交通运输厅公路规划勘察设计研究院,成都 610065
2. State Key Laboratory of Hydraulics and Mountain River Engineering (Sichuan University), Chengdu 610065, China;
3. Sichuan Provincial Transport Department Highway Planning, Survey, Design and Research Institute, Chengdu 610065, China
工程建设中的岩体[1]多含非贯通节理,在外力作用下的损伤由细观损伤和宏观节理损伤组成.针对细观损伤本构模型,Weibull[2]首次基于统计理论提出强度分布函数,称为Weibull分布函数.众多学者基于岩石单元强度服从Weibull函数分布,推导出细观损伤变量表达式[3-4].针对岩体的损伤本构模型,Kyoya等[5]首次将损伤力学理论引入到节理岩体的研究,通过二阶对称张量来反映宏观节理的各向异性特征,采用有效应力方法建立起节理岩体的本构关系,将节理的几何特征和力学特性有效联系起来, 从而为节理岩体的研究提供了新思想.基于这种新思想,Chen等[6]将损伤变量定义为节理频率,采用平行等间距节理与岩石弹性矩阵相复合的方法,推导出节理岩体的微平面本构模型;陈文玲等[7]从应变能释放量出发,基于连续 (半连续) 介质力学推导出了宏观损伤张量的计算表达式.
目前已发表的成果[6-7]多依据初始宏观节理的排距和贯通率引入修正系数以考虑节理间的相互影响,取值多具经验性;现有文献中的复合损伤本构模型并没有考虑宏观节理损伤演化的影响.为此,本文在前人研究基础上,针对非贯通节理岩体,引用自洽方法[8]考虑节理之间的相互作用,并采用逐条添加节理的方法进行修正,基于Betti能量互易定理[8],推导出岩体不同受力阶段的复合损伤本构模型.
1 细观损伤演化本构模型 1.1 模型的建立假设岩石的强度服从Weibull分布[3-4],微元体的总数目为Z,某一荷载作用下,破坏的微元数目为Zi.由于实际岩石残余损伤变量小于1,故引入折减系数η(0≤η<1),则损伤变量表达式为[9]
| $ {{D'}_1} = \eta \frac{{{Z_i}}}{Z} = \eta \left( {1 - \exp {{\left[ { - \left( {\frac{F}{{{F_0}}}} \right)} \right]}^m}} \right). $ | (1) |
假定岩石微单元破坏前服从胡克定律,根据Lemaitre有效应力定义,可得损伤统计本构模型[9]:
| $ \begin{array}{l} {\sigma _i} = {{\sigma '}_i}\left( {1 - {{D'}_1}} \right) = E{\varepsilon _i}\left( {1 - \eta + \eta \exp {{\left[ { - \left( {\frac{F}{{{F_0}}}} \right)} \right]}^m}} \right) + \\ \;\;\;\;\;\;\;\mu \left( {{\sigma _j} + {\sigma _k}} \right). \end{array} $ | (2) |
式中:σi为名义应力,σ′i为有效应力, E、εi分别为完整岩石的弹性模量和应变, σj、σk为围压.
设有效主应力σ′1≥σ′2≥σ′3,本文采用应用最广泛的Mohr-Coulomb准则,其表示式为
| $ F = {{\sigma '}_1} - {{\sigma '}_3} - \left( {{{\sigma '}_1} + {{\sigma '}_3}} \right)\sin \varphi = 2c\cos \varphi . $ | (3) |
式中c、φ分别为材料的粘聚力和摩擦角.
根据Lemaitre应变等效假设和胡克定律,有效应力与名义应力有以下关系式[10]:
| $ {{\sigma '}_1} = \frac{{E{\varepsilon _1}{\sigma _1}}}{{{\sigma _1} - 2\mu {\sigma _3}}}, $ | (4) |
| $ {{\sigma '}_3} = \frac{{E{\varepsilon _1}{\sigma _3}}}{{{\sigma _1} - 2\mu {\sigma _3}}}. $ | (5) |
设岩石峰值处的应力和应变分别为σc和εc,残余强度处的应力和应变分别为σu和εu,通过式 (4)~(5) 可得荷载峰值和残余强度的F值,引入3个条件:
| $ {S_1} = F\left| {_{{\sigma _1} = {\sigma _{\rm{c}}},{\varepsilon _1} = {\varepsilon _{\rm{c}}}}} \right., $ | (6) |
| $ {S_2} = F\left| {_{{\sigma _1} = {\sigma _{\rm{u}}},{\varepsilon _1} = {\varepsilon _{\rm{u}}}}} \right., $ | (7) |
| $ {{S'}_1} = \frac{{{\rm{d}}F}}{{{\rm{d}}{\varepsilon _1}}}\left| {_{{\sigma _1} = {\sigma _{\rm{c}}},{\varepsilon _1} = {\varepsilon _{\rm{c}}}}} \right.. $ | (8) |
将式 (6)~(8) 代入式 (2),分布参数m、F0、η可通过以下3式联列计算得出:
| $ m = - {U_4} \times {\left( {{U_3} \times {{S'}_1} \times {U_2}} \right)^{ - 1}}, $ | (9) |
| $ {F_0} = \frac{{{S_1}}}{{{{\left( { - \ln \left[ {\frac{{{\sigma _{\rm{c}}} - 2\mu {\sigma _3}}}{{\eta E{\varepsilon _{\rm{c}}}}} - \frac{1}{\eta } + 1} \right]} \right)}^{\frac{1}{m}}}}}, $ | (10) |
| $ {S_1} = \ln \frac{{{S_1}}}{{{S_2}}} + {U_1} \times {U_3} \times {{S'}_1} \times {U_2} \times U_4^{ - 1} = 0. $ | (11) |
式中:
应当注意,式 (11) 是一个隐式方程,需通过迭代方式求解.
2 复合损伤变量基于损伤力学理论,将损伤等效为弹性模量的弱化,节理岩体的损伤本构关系可表示为[11]
| $ \sigma = {E^ * }{\varepsilon _i} = E{\varepsilon _i}\left( {1 - D} \right). $ | (12) |
式中:E*为岩体的弹性模量,D为岩体的复合损伤变量,σ为单轴压缩应力.
2.1 附加应变能的计算在单轴压缩应力σ作用下,根据Betti能量互易定律得如下关系式[8]:
| $ \frac{{{\sigma ^2}V}}{{2{E^ * }}} = \frac{{{\sigma ^2}V}}{{2E}} + \Delta {\varphi _1} + \Delta {\varphi _2} + \Delta {\varphi _3}. $ | (13) |
式中:V为试件的体积,Δφ1为细观损伤产生的附加应变能,Δφ2为初始节理产生的附加应变能,Δφ3为节理损伤演化产生的附加应变能.
1)Δφ1的计算.在单轴应力σ作用下,Δφ1通过细观损伤变量D′1,由式 (14) 计算[7]:
| $ \Delta {\varphi _1} = {\sigma ^2}V\left[ {\frac{1}{{2E\left( {1 - {{D'}_1}} \right)}} - \frac{1}{{2E}}} \right]. $ | (14) |
2)Δφ2的计算.对于平面应力问题,单个节理引起的附加应变能通过式 (15) 计算[8]:
| $ {U_{\rm{e}}} = \frac{T}{E}\int_0^c {\left( {K_{\rm{I}}^2 + K_{{\rm{II}}}^2} \right){\rm{d}}c} . $ | (15) |
式中:KⅠ、KⅡ分别为节理尖端的Ⅰ、Ⅱ型有效应力强度因子,中心节理T=2,单边节理T=1,c为节理半长.
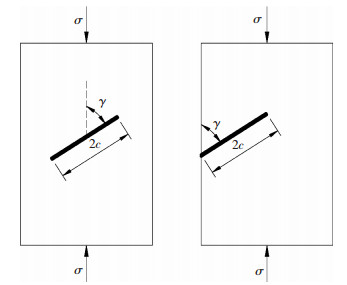
如图 1所示,闭合节理面的Ⅰ型有效应力强度因子等于零[7].参照袁小清等[11]和Isida[12]的研究成果,按节理长度和平板宽度进行修正,可得Ⅱ型有效强度因子表达式[13] :
| $ {K_{{\rm{II}}}} = {c_{\rm{v}}}\sigma \sqrt {\pi a} \sin \gamma \cos \gamma \sqrt {\sec \left( {\frac{{\pi a}}{w}} \right)} . $ | (16) |
|
图 1 单节理受力简图 Figure 1 Single crack force diagram |
式中:中心节理a=c,单边节理a=2c,w为平板的宽度,cv为传剪折减系数.
将式 (16) 代入式 (15),含有N条节理试件的初始节理损伤附加应变能可表示为[8]
| $ \Delta {\varphi _2} = Nc_{\rm{v}}^2{\sigma ^2}\pi {a^2}{\sin ^2}\gamma {\cos ^2}\gamma \sec \sqrt {\frac{{\pi a}}{w}} \frac{T}{{2E}}. $ | (17) |
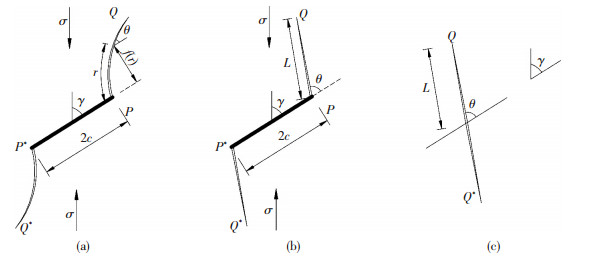
3)Δφ3的计算.压缩应力到一定值后,节理尖端开始扩展演化,见图 2(a),PP*为初始节理,PQ、P*Q*为节理演化轨迹,Horii等[14]给出了图 2(a)的精确解,但是由于公式复杂,不利于计算,根据Horii等[15]的研究,将图 2(a)等效为图 2(b)、(c)直线裂纹.
|
图 2 裂纹扩展模型 Figure 2 Crack propagation model |
根据Paul[16]的成果, 图 2(c)中Ⅰ型有效应力强度因子可表示为
| $ {K_1} = M\left( {\sqrt {2a + L} - \sqrt L } \right)\sqrt {\frac{\pi }{2}} + {N_1}\sqrt {\frac{{\pi L}}{2}} . $ | (18) |
式中:
根据Kemeny等[13]的研究成果,节理扩展演化方式以Ⅰ型断裂为主.根据式 (18) 和式 (15),利用Maple17.0进行计算, 得N条节理损伤演化引起的附加应变能表达式为
| $ \Delta {\varphi _3} = TN\int_0^L {K_1^2{\rm{d}}L} = TN\left( {{M^2}{P_1} + {P_2} + {P_3} + {P_4}} \right). $ | (19) |
式中:P1=3.12aL+1.56L2-1.562
裂纹扩展直至KI=KIC停止扩展,因此式 (18) 中,令KI=KIC,便可计算得出节理演化长度L[12].
2.2 复合损伤变量的计算假设宏观损伤演化过程中裂纹的数目不发生变化,根据Kemeny[8]的研究成果,采用自洽方法考虑多条节理之间的相互作用,近似假设节理周围单元体的弹性模量均为初始损伤体的名义弹模.因此,将式 (17) 中的E以名义弹性模量E*代替,将式 (14)、(17) 和式 (19) 代入式 (13) 整理可得:
| $ \frac{{{E^ * }}}{E} = \left( {1 - {{D'}_1}} \right)\left( {1 - TP\pi G - \frac{{2T{P_5}}}{{{c^2}{\sigma ^2}}}G} \right), $ | (20) |
式中:
这里,定义G为节理密度[8].Kemeny[8]和Bruner[17]提出了修正自洽方法,即岩体中依次添加单条节理,每次节理添加后对应的岩体弹性模量是一个变化值,从第一条节理添加前的岩石弹性模型E变化到最后一条节理添加完毕后对应的岩体名义弹性模量E*.对式 (20) 以G为变量进行微分,并以E*代替E,得以下方程和相应的初始条件:
| $ \frac{{{\rm{d}}{E^ * }}}{{{\rm{d}}G}} = - T\left( {1 - {{D'}_1}} \right)P\pi {E^ * } - \frac{{2T{P_5}}}{{{c^2}{\sigma ^2}}}\left( {1 - {{D'}_1}} \right){E^ * }, $ | (21) |
| $ {E^ * }\left( 0 \right) = E\left( {1 - {{D'}_1}} \right). $ | (22) |
根据式 (21)、(22) 的解,可得3种复合损伤的损伤变量表达式:
| $ \begin{array}{l} D = 1 - \left( {1 - {{D'}_1}} \right)\exp \left( { - T\left( {1 - {{D'}_1}} \right)PG\pi - } \right.\\ \;\;\;\;\;\;\;\left. {\frac{{2T{P_5}}}{{{c^2}{\sigma ^2}}}G\left( {1 - {{D'}_1}} \right)} \right). \end{array} $ | (23) |
由于宏观节理及其损伤演化具有各向异性,因此需要对应力作用方向上的损伤进行张量化,本文采用Toshikazu等[18]的方法进行张量化.
1) 对于单组非贯通节理,根据图 1,设非贯通节理的法向向量为n,则有
| $ \mathit{\boldsymbol{e = n}} \otimes \mathit{\boldsymbol{n}} = \left[ {\begin{array}{*{20}{c}} {{{\sin }^2}\gamma }&{\sin \gamma \cos \gamma }\\ {\sin \gamma \cos \gamma }&{{{\cos }^2}\gamma } \end{array}} \right]. $ | (24) |
2) 对于多组非贯通节理张量的计算方法:设有W组节理,法向向量为ni (i=1, 2, …),则
| $ {\mathit{\boldsymbol{e}}^i} = {\mathit{\boldsymbol{n}}^i} \otimes {\mathit{\boldsymbol{n}}^i} $ | (25) |
| $ {\mathit{\boldsymbol{e}}_{ij}} = \frac{1}{W}\sum\limits_{b = 1}^W {\mathit{\boldsymbol{e}}_{ij}^b} \;\;\;\left( {i,j = 1,2,3, \cdots } \right) $ | (26) |
岩体损伤分为3个阶段:加载初期为初始节理宏观损伤;加载中期为初始节理损伤和细观损伤的复合;加载后期为初始节理损伤、细观损伤、节理演化损伤的复合.根据式 (23) 可得不同加载阶段的复合损伤变量表达式:
| $ D = \left\{ {\begin{array}{*{20}{c}} {1 - \exp \left( { - T{e_1}P\pi G} \right),}\\ {1 - \left( {1 - {{D'}_1}} \right)\exp \left( { - T{e_1}\left( {1 - {{D'}_1}} \right)PG\pi } \right),}\\ {1 - \left( {1 - {{D'}_1}} \right)\exp \left( { - T{e_1}\left( {1 - {{D'}_1}} \right)PG\pi - \frac{{2T{e_2}{P_5}}}{{{c^2}{\sigma ^2}}}G\left( {1 - {{D'}_1}} \right)} \right),} \end{array}} \right.\begin{array}{*{20}{c}} {加载初期\left( {F < {F_{\rm{s}}}\left( {1 - {{D'}_1}} \right),{K_{\rm{I}}} < {K_{{\rm{IC}}}}} \right);}\\ {加载中期\left( {F \ge {F_{\rm{s}}}\left( {1 - {{D'}_1}} \right),{K_{\rm{I}}} < {K_{{\rm{IC}}}}} \right);}\\ {加载后期\left( {F \ge {F_{\rm{s}}}\left( {1 - {{D'}_1}} \right),{K_{\rm{I}}} < {K_{{\rm{IC}}}}} \right).} \end{array} $ | (27) |
式中: e1和e2分别为初始节理和节理演化损伤计算得出的应力作用方向标量值, 根据式 (24)~(26) 计算; Fs为完整岩石屈服强度.
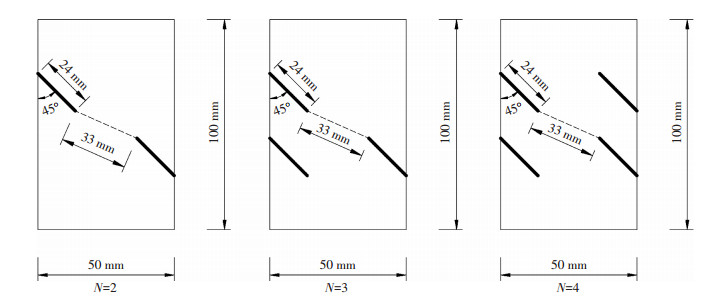
3 算例分析为验证本文所建模型的合理性和有效性,采用杨圣奇等[19]断续非贯通节理脆性大理岩的室内试验成果进行对比分析,鉴于研究三维断裂问题存在一定困难,可将三维问题概化为二维问题进行研究,文献[19]中节理个数概化后的平面模型见图 3.
|
图 3 二维概化模型 Figure 3 Two-dimensional generalized model |
根据文献[19]完整岩石应力应变曲线可以看出,单轴压缩初期,存在明显的压密段.为更直观地证明模型的合理性,对室内试验曲线进行修正,方法为室内试验应力应变曲线减去压密段引起的附加应变,得到修正后室内试验应力应变曲线.脆性大理岩的粘聚力为31.64 MPa,内摩擦角为22.5°,泊松比为0.25,根据修正后的完整岩石应力应变曲线,由式 (9)~(10) 计算得出细观损伤最优参数为m=11.359,F0=69.13,η=0.997.
文献[19]中预制节理中填充有软石膏,故按闭合节理处理,根据Toshikazu等[18]提出的试算方法,得到传剪折减系数cv=0.46.加载初期,预制节理的夹角为45°,可得初始节理的二阶对称张量为
| $ {\mathit{\boldsymbol{e}}_{ij}} = \left[ {\begin{array}{*{20}{c}} {0.5}&{0.5}\\ {0.5}&{0.5} \end{array}} \right]. $ |
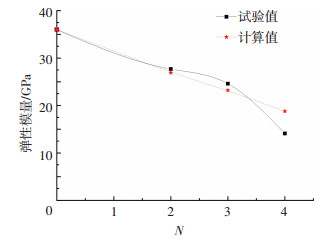
根据初始节理的二阶对称张量和式 (27) 计算加载初期的宏观损伤变量D,再由式 (12) 计算可得不同节理个数的等效弹性模量,图 4给出初始损伤体弹性模量随节理个数的变化曲线.
|
图 4 弹性模量对比曲线 Figure 4 Correlation curve of the elastic modulus |
由文献[19]试验结果可看出,节理岩体荷载峰值前出现应力下坠点,可认为此时节理开始损伤演化[19-20],且节理演化长度保持不变[19-20];由于文献[19]中没有岩体的断裂韧度,根据文献[19]的试验结果和文献[21]的研究成果,取文献[19]中岩体的受压Ⅰ型断裂韧度为6.96 MPa·m1/2;根据节理演化的起裂角70.5°,可得节理演化引起的二阶对称张量为
| $ {\mathit{\boldsymbol{e}}_{ij}} = \left[ {\begin{array}{*{20}{c}} {0.81}&{0.39}\\ {0.39}&{0.19} \end{array}} \right]. $ |
随着轴向应力的下坠,岩体的损伤为细观、初始节理、节理扩展演化3种损伤的复合.节理的起裂长度,可根据Ⅰ型断裂韧度由式 (18) 计算得出.根据损伤变量的定义,岩体的荷载峰值强度为
| $ {\sigma _{\rm{c}}} = E\left( {1 - D} \right){\varepsilon _{\rm{c}}}. $ | (28) |
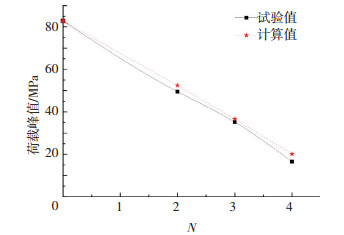
图 5给出荷载峰值随节理个数的变化曲线.由图 4、5可知,N为2、3和4的岩体,室内试验与理论计算的弹性模量、荷载峰值均有较好的吻合度,由此可证明本文损伤变量理论值的正确性.
|
图 5 荷载峰值曲线 Figure 5 The peak load curve |
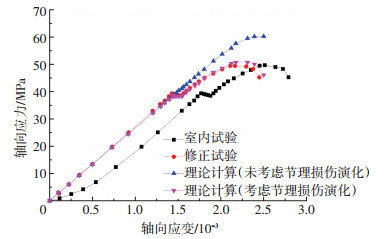
根据式 (12) 和式 (27) 分别计算考虑节理损伤演化和未考虑节理损伤演化的理论应力应变曲线,并与室内试验曲线、修正的室内试验曲线进行对比,这里给出N=2的拟合结果,见图 6.
|
图 6 室内试验与计算结果对比 Figure 6 Comparison of experiment and calculation results |
由图 6可看出,室内试验显示节理岩体荷载峰值前出现了明显的应力低落,考虑节理损伤演化的理论曲线较好拟合了修正后室内试验结果.分析认为,节理损伤演化会引起损伤变量增加,岩体弹性模量的降低,对其力学特性有重要影响.
4 结论本文针对非贯通闭合节理岩体,从附加应变能增量和损伤应变能释放量相关联的思路出发,基于Betti能量互易定理,采用修正自洽方法推导岩体单轴压缩不同受力阶段的复合损伤本构模型:
1) 将本文模型的理论计算结果与室内试验结果进行对比分析,本文模型的理论计算结果与室内试验结果规律一致,随着节理个数的增加,初始弹性模量和荷载峰值均呈下降趋势,下降幅度较为一致;节理的损伤演化对岩体的力学特性有重要影响,考虑节理损伤演化的理论应力应变曲线和荷载峰值与室内试验结果更为吻合,有效验证了本文复合损伤本构模型的正确性和合理性.
2) 岩体断裂韧度根据远场应力计算求得,并不完全准确.同时,由于峰后节理损伤演化轨迹的复杂性,需要对峰后节理演化以及有限边界的有效应力强度因子理论做进一步探索,以得到更为精确的结果;本文假设岩体中的细观损伤依然符合统计损伤模型,更为准确的含节理岩体细观损伤模型有待进一步研究.
| [1] |
卢志堂, 王志亮. 近场动力学法频散特性及其在岩石层裂分析中应用[J].
哈尔滨工业大学学报, 2016, 48(2): 131-137.
LU Zhitang, WANG Zhiliang. Dispersion characteristics of peridynamics method and its application[J]. Journal of Harbin Institute of Technology, 2016, 48(2): 131-137. DOI: 10.11918/j.issn.0367-6234.2016.02.022 |
| [2] | WEIBULL W. A statistical distribution function of wide applicability. Journal of Applied Mechanics[J].1951, 18:293-297. |
| [3] | WANG Zhiliang, LI Yongchi, WANG J G. A damage-softening statistical constitutive model considering rock residual strength[J]. Computers & Geosciences, 2007, 3: 1-9. |
| [4] |
曹文贵, 张升, 赵明华. 软化与硬化特性转化的岩石损伤统计本构模型之研究[J].
工程力学, 2006, 23(11): 110-115.
CAO Wengui, ZHANG Sheng, ZHAO Minghua. Study on a statistical damage constitutive model with conversion between softening and hardening properties of rock[J]. Engineering Mechanics, 2006, 23(11): 110-115. DOI: 10.3969/j.issn.1000-4750.2006.11.018 |
| [5] | KYOYA T, ICHIKAWA Y, KAWAMOTO T A. Damage mechanics theory for discontinuous rock mass[C]//5th International Conference on Numerical Methods in Geomechanics. Innsbruck:[s.n.], 1985: 469-480. |
| [6] | CHEN Xin, ZDENEK P B. Microplane damage model for jointed rock masses[J]. International journal for numerical and analytical methods in geomechanics, 2014, 38(14): 1431-1452. DOI: 10.1002/nag.v38.14 |
| [7] |
陈文玲, 李宁. 含非贯通裂隙岩体介质的损伤模型[J].
岩土工程学报, 2000, 22(4): 430-434.
CHEN Wenling, LI Ning. Damage model of the rock mass medium with intermittent cracks[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(4): 430-434. |
| [8] | KEMENY J. Effective moduli, non-linear deformation and strength of a cracked elastic solid[J]. Int.J.Rock.Mech.Min, 1986, 23(2): 107-118. DOI: 10.1016/0148-9062(86)90337-2 |
| [9] |
曹瑞琅, 贺少辉, 韦京, 等. 基于残余强度修正的岩石损伤软化统计本构模型研究[J].
岩土力学, 2013, 34(6): 1652-1660.
CAO Ruilang, HE Shaohui, WEI Jing, et al. Study of modified statistical damage softening constitutive model for rock considering residual strength[J]. Rock and Soil Mechanics, 2013, 34(6): 1652-1660. DOI: 10.16285/j.rsm.2013.06.018 |
| [10] |
张明, 王菲, 杨强. 基于三轴压缩试验的岩石统计损伤本构模型[J].
岩土工程学报, 2013, 35(11): 1965-1971.
ZHANG Ming, WANG Fei, YANG Qiang. Statistical damage constitutive model for rocks based on triaxial compression tests[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(11): 1965-1971. |
| [11] |
袁小清, 刘红岩, 刘京平. 基于宏细观损伤耦合的非贯通裂隙岩体本构模型[J].
岩土力学, 2015, 36(10): 2804-2813.
YUAN Xiaoqing, LIU Hongyan, LIU Jingping. Constitutive model of rock mass with non-persistent joints based on coupling macroscopic and mesoscopic damages[J]. Rock and Soil Mechanics, 2015, 36(10): 2804-2813. DOI: 10.16285/j.rsm.2015.10.009 |
| [12] | ISIDA M. On the tension of a strip with a central elliptical hole[J]. Transactions of the Japan Society of Mechanical Engineering, 1955, 21(107): 507-518. DOI: 10.1299/kikai1938.21.507 |
| [13] | KEMENY J M, COOK N G W. Micromechanics of deformation in rocks[J]. Toughening Mechanisms in Quasi-Brittle Materials, 1991, 195: 155-188. |
| [14] | HORⅡ S, NEMAT N. Estimate of stress intensity factor for interacting cracks[J]. In Advances in Aerospace Structures, materials and dynamics, 1983, 6: 111-117. |
| [15] | HORⅡ S, NEMAT N. Brittle failure in compression: splitting, faulting and brittle-ductile transition[J]. Phil. Mathematical and Physical Sciences, 1996, 319(1549): 319, 337-374. |
| [16] | PAUL S. Crack extension under compressive loading[J]. Engineering Fracture Mechanics, 1984, 3: 463-473. |
| [17] | BRUNER W M. Comment on seismic velocities in dry and statured cracked solids by Oconnell budiansky[J]. Geophys Res, 1976, 81: 2573-2576. DOI: 10.1029/JB081i014p02573 |
| [18] | TOSHIKAZU K, YASUAKI I, TAKASHI K. Deformation and fracturing behavior of discontinuous rock mass and damage mechanics theory[J]. International Journal for Numerical and Analytical Method in Geomechanics, 1988, 12(1): 1-30. DOI: 10.1002/(ISSN)1096-9853 |
| [19] |
杨圣奇, 戴永浩, 韩立军, 等. 断续预制裂隙脆性大理岩变形破坏特性单轴压缩试验研究[J].
岩石力学与工程学报, 2009, 28(12): 2391-2404.
YANG Shengqi, DAI Yonghao, HAN Lijun, et al. Uniaxial compression experimental research on deformation and failure properties of brittle marble specimen with pre-existing fissures[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(12): 2391-2404. DOI: 10.3321/j.issn:1000-6915.2009.12.003 |
| [20] |
杨圣奇. 断续三裂隙砂岩强度破坏和裂纹扩展特征研究[J].
岩土力学, 2013, 34(1): 31-39.
YANG Shengqi. Study of strength failure and crack coalescence behavior of sandstone containing three pre-existing fissures[J]. Rock and Soil Mechanics, 2013, 34(1): 31-39. DOI: 10.16285/j.rsm.2013.01.009 |
| [21] |
崔智丽. 岩石类材料中心裂纹圆盘试件动态断裂韧性测试系统的动力学有限元分析及测试方法的研究[D]. 安徽: 安徽理工大学, 2011.
CUI Zhili. Research on dynamics finite element analysis and testing methods of dynamic fracture toughness test system of central cracked circular disk specimen of rock[D].Anhui: Anhui University of Science and Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10361-1011245998.htm |
 2017, Vol. 49
2017, Vol. 49


