由于采光通风,集装箱房需要开洞处理,但这会削弱其抗侧刚度.因此,应对开洞形式进行限制.目前,国内外针对集装箱房的研究主要集中在运输、建筑领域[1-6],对其结构力学性能的研究[7-10],尤其是开洞集装箱抗侧刚度方面的研究非常少.集装箱房多采用叠箱结构,犹如堆积木,其水平荷载主要来自地震作用,集中在每一层楼面上,在上下层间层层传递.层间连接件越多,荷载传递越均匀,局部效应越小,抗侧刚度越大.由于开洞集装箱的蒙皮效应被削弱,其层间连接件相对整箱应更密集,层间水平力趋于均布,而目前少量的开洞集装箱抗侧刚度研究[11-15]均针对集中荷载,不符合实际.
集装箱抗侧刚度主要来源于蒙皮效应,求解开洞影响的关键则在于分析侧板蒙皮效应的削弱.欧洲蒙皮理论[16-18]对开洞蒙皮体有较深入的研究,且其螺栓连接蒙皮结构的受力、变形较均匀,和均布荷载作用的集装箱类似.因此,本文选择借鉴欧洲蒙皮理论,基于其权威书籍《欧洲钢结构应力蒙皮设计推荐》[16]、《受力蒙皮设计手册》[17],对集装箱侧板开洞形式进行限定;基于能量理论,结合有限元数值模拟,针对均布荷载作用下的开洞集装箱抗侧刚度及限定细则的合理性进行推导、论证,并用已有试验数据对有限元建模方法进行验证.
1 基于欧洲蒙皮理论的开洞形式
|
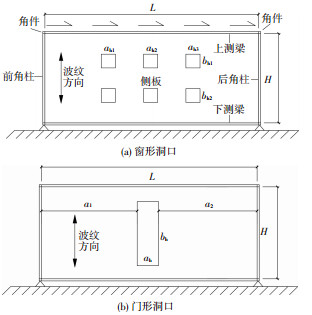
图 1 集装箱侧板开洞的两种形式 Figure 1 Two opening types of container side plate |
欧洲蒙皮理论分别对两种洞口形式进行了规定和限制,将其移植到集装箱房.
窗形洞口应满足3点要求:
1) 洞口应按行列对齐分布;
2) 洞口总高度不超过侧板总高度的1/3;
3) 洞口间距及到边缘的距离至少等于洞口的宽度.
门形洞口应满足3点要求:
1) 洞口总高度超过侧板总高度2/3;
2) 洞口的宽度不超过侧板总长度的25%;
3) 洞口两侧的距离——a1和a2相差不超过20%.
2 开洞抗侧刚度计算理论均布荷载下,集装箱侧板开洞会导致其抗侧刚度发生明显折减,具体计算式为
| $ {{K'}_{\rm{z}}} = \kappa \times {K_{\rm{z}}}, $ | (1) |
式中:Kz′为均布荷载下,开洞后的集装箱抗侧刚度;Kz为均布荷载下,整箱的抗侧刚度;κ为均布荷载下,刚度折减系数.
从式 (1) 可看出,确定开洞集装箱抗侧刚度的关键在于求解不同的洞口形式所对应的折减系数κ.
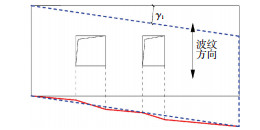
2.1 窗形开洞根据欧洲蒙皮理论,满足限制的开洞并不会让蒙皮结构的变形机理产生本质变化.因此,开洞侧板仍仅发生剪切变形,但开洞会导致蒙皮板沿长度方向的变形不再连续,见图 2中实折线.然而,由于集装箱上下侧梁同蒙皮板焊接,二者变形相互协调;且由于洞口尺寸的限制,使得洞口区域的变形突变并不大,因此其最终变形仍然趋于平滑,见图 2中虚线.由于蒙皮板仅受剪力作用,不考虑弯曲变形,根据欧洲蒙皮理论,可近似认为它两个方向的剪应变互等.
|
图 2 窗形开洞的侧板剪切变形 Figure 2 The shear deformation of side plate with window shaped openings |
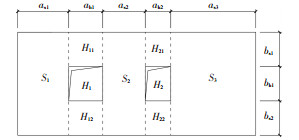
根据以上分析,以洞口左右两侧边缘为边界对蒙皮板进行分割,划分成若干区域,见图 3.将洞口从左到右依次命名为Hi,将区域内不带洞口的板块从左到右依次命名为Sk,将区域内带洞口的板块命名为Hij,其中i代表板块所在的洞口区域,j代表板块在区域内的上下位置.由于欧洲蒙皮理论并未对洞口四周是否加固进行要求,因此,分窗形洞口加固与不加固进行讨论.
|
图 3 窗形开洞的侧板区域划分 Figure 3 The division of side plate with window openings |
在开洞区域的板块,其变形会发生突变,大于相邻的完整未开洞板块.造成这种现象的原因是开洞板块的受力蒙皮面积减少,同时应力会在洞口上下的板块间重分布.对板块H11进行分析,通过能量理论可以求得其纯剪应变能,然后通过卡氏第二定理可以得到其纯剪柔度,见式 (2);以及扭曲柔度,见式 (3).
| $ {c_{{\rm{11j}}}} = {\varphi _{\rm{j}}}\frac{{2{a_{{\rm{h1}}}}\left( {1 + \nu } \right)}}{{{b_{{\rm{s1}}}}tE}}, $ | (2) |
| $ {c_{{\rm{11n}}}} = {\varphi _{\rm{n}}}\frac{{{a_{{\rm{h1}}}}\left( {1 - {\nu ^2}} \right)}}{{Ed{t^3}d_{{\rm{s1}}}^3}}. $ | (3) |
式中:φj、φn是仅和波纹形状有关的参数,按整箱的理论计算;ν是泊松比;E是钢材弹性模量;t是侧板厚度;d是一个波纹单元的水平投影长度.
同理,可得到板块H12的纯剪柔度及扭曲柔度,然后根据变形协调原理按刚度对H11、H12进行受力分配,可得到板块H11的纯剪作用引起的侧移ΔH11j,及扭曲作用引起的侧移ΔH11n,二者之和即该区域的总剪切变形.
| $ \Delta _{{{\rm{H}}_{{\rm{11}}}}}^{\rm{j}} = {c_{{\rm{11j}}}} \times {P_1} = {\varphi _{\rm{j}}}\frac{{2{a_{{\rm{h1}}}}{\alpha _{\rm{s}}}\left( {1 + \nu } \right)}}{{\left( {{b_{{\rm{s1}}}} + {b_{{\rm{s2}}}}} \right)tE}}P, $ | (4) |
| $ \Delta _{{{\rm{H}}_{{\rm{11}}}}}^{\rm{n}} = {c_{{\rm{11n}}}} \times {P_1} = {\varphi _{\rm{n}}}\frac{{{a_{{\rm{h1}}}}\left( {1 - {\nu ^2}} \right)}}{{Ed{t^3}\left( {b_{{\rm{s1}}}^3 + b_{{\rm{s2}}}^3} \right)}}. $ | (5) |
式中P是集装箱侧板所受的总剪力,P1是板块H11所受剪力.
对于无开洞的板块S1,可以直接通过能量理论求得其剪切变形以及扭曲变形:
| $ \Delta _{{\rm{S1}}}^{\rm{j}} = {\varphi _{\rm{j}}}\frac{{2{a_{{\rm{h1}}}}{\alpha _{\rm{s}}}\left( {1 + \nu } \right)}}{{btE}}P, $ | (6) |
| $ \Delta _{{\rm{S1}}}^{\rm{n}} = {\varphi _{\rm{n}}}\frac{{{a_{{\rm{s1}}}}\left( {1 - {\nu ^2}} \right)}}{{Ed{t^3}{b^3}}}P. $ | (7) |
式中b代表侧板的总高度,同集装箱高度H近似相等.
同上,可求出其他开洞板块和不开洞板块的相应变形,进而得到总的纯剪变形以及总的纯扭曲变形:
| $ \begin{array}{l} \Delta _{\rm{h}}^{\rm{j}} = \sum {\Delta _{{\rm{S}}i}^{\rm{j}}} + \sum {\Delta _{{\rm{H}}i}^{\rm{j}}} = {\varphi _{\rm{j}}}\frac{{2\sum {{a_{{\rm{s}}i}}{\alpha _{\rm{s}}}\left( {1 + \nu } \right)P} }}{{btE}} + \\ \;\;\;\;\;\;\;{\varphi _{\rm{j}}}\frac{{2\sum {{a_{{\rm{h}}i}}{\alpha _{\rm{s}}}\left( {1 + \nu } \right)P} }}{{\sum {{b_{{\rm{s}}i}}tE} }}, \end{array} $ | (8) |
| $ \begin{array}{l} \Delta _{\rm{h}}^{\rm{n}} = \sum {\Delta _{{\rm{S}}i}^{\rm{n}}} + \sum {\Delta _{{\rm{H}}i}^{\rm{n}}} = {\varphi _{\rm{n}}}\frac{{\sum {{a_{{\rm{s}}i}}\left( {1 + {\nu ^2}} \right)} }}{{Ed{t^3}{b^3}}}P + \\ \;\;\;\;\;\;\;{\varphi _{\rm{n}}}\frac{{\sum {{a_{{\rm{h}}i}}\left( {1 + {\nu ^2}} \right)} }}{{Ed{t^3} \times \sum {b_{{\rm{s}}i}^3} }}P. \end{array} $ | (9) |
分别将Δhj、Δhn与相同尺寸无洞口整板的纯剪切变形、扭曲变形相比,即可得到相应的变形增大系数:
| $ {\lambda _{\rm{j}}} = \frac{{{a_{\rm{s}}}}}{L} + \frac{H}{L} \times \frac{{{a_{\rm{h}}}}}{{{b_{\rm{s}}}}}, $ | (10) |
| $ {\lambda _{\rm{n}}} = \frac{{{a_{\rm{s}}}}}{L} + \frac{{{a_{\rm{h}}}}}{L}\frac{{{H^3}}}{{\sum {b_{{\rm{s}}i}^3} }}. $ | (11) |
式中:as=L-ah, bs=H-bh, ah=
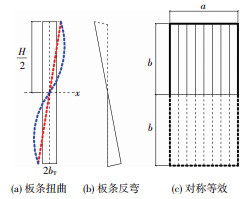
对于无加固处理的窗形开洞,洞口上下边缘自由,扭曲变形会随着边界条件的改变而变化.因此,应在加固的窗形洞口的基础之上考虑由于洞口边界条件变化引起的附加扭曲变形.由于没有加固处理,洞口四周形成自由的边界.对于无洞口的区域Sk,其上下边缘仍然与上下侧梁固定连接,受到约束,仅左右侧小部分区域形成自由边界,其扭曲变形几乎不受影响;对于洞口区域的板块Hij,边界条件变为一端固结一端自由,其扭曲变形将发生改变.取一个波纹的侧部板条分析,见图 4(a),长度为H,宽度为2bT.剪力作用下,当其边界条件为螺栓连接时,扭曲变形表现为非线性,见图 4(a)中弯曲的虚线;而对于焊接蒙皮结构,其扭曲变形是线性的,见图 4(a)中平直的虚线.无论是线性扭曲还是非线性扭曲,其变形都相对x轴反对称,在高度一半处发生类似“反弯”的现象,见图 4(b).对于板块Hij,其变形同左右两侧刚性板块相协调,仍以线性扭曲为主,但却不会在其二分之一高度处发生“反弯”.假设一块板的高度是开洞板块的一倍,其余参数完全相同,两端固结,见图 4(c).那么其“反弯”点正好出现在开洞板块下边缘的位置.由于反弯点上下部分是完全对称的,则其变形能完全相同,等于总变形能的一半.
|
图 4 波纹板扭曲变形分析示意 Figure 4 Distortion deformation analysis of corrugated plate |
根据能量理论结构力学,扭曲应变能同压型钢板高度b的三次方成正比且扭曲柔度同扭曲应变能成正比.因此,一条边界自由对蒙皮板扭曲柔度产生的放大系数:
| $ {\lambda _{\rm{b}}} = \frac{{\frac{1}{2} \times {{\left( {2b} \right)}^3}}}{{{b^3}}} = 4. $ | (12) |
可得到考虑无加固影响的板块H11的扭曲变形:
| $ \Delta _{{{\rm{H}}_{11}}}^{{\rm{n'}}} = 4{\varphi _1}\frac{{{a_{{\rm{h1}}}}\left( {1 - {\nu ^2}} \right)}}{{Ed{t^3}\left( {b_{{\rm{s1}}}^3 + b_{{\rm{s2}}}^3} \right)}}P. $ | (13) |
同理,可以求解出其他板块的考虑无加固影响的扭曲变形,进而得到总的扭曲变形Δhn′以及相应的修正后的扭曲变形增大系数λn′:
| $ \begin{array}{l} \Delta _{\rm{h}}^{{\rm{n'}}} = \sum {\Delta _{{\rm{S}}i}^{{\rm{n'}}}} + \sum {\Delta _{{\rm{H}}i}^{{\rm{n'}}}} = {\varphi _1}\frac{{\sum {{a_{{\rm{s}}i}}\left( {1 - {\nu ^2}} \right)P} }}{{Ed{t^3}{b^3}}} + \\ \;\;\;\;\;\;4{\varphi _1}\frac{{\sum {{a_{{\rm{h}}i}}\left( {1 - {\nu ^2}} \right)P} }}{{Ed{t^3} \times \sum {b_{{\rm{s}}i}^3} }}, \end{array} $ | (14) |
| $ {{\lambda '}_{\rm{n}}} = \frac{{{a_{\rm{s}}}}}{L} + 4 \times \frac{{{a_{\rm{h}}}}}{L}\frac{{{H^3}}}{{\sum {b_{{\rm{s}}i}^3} }}. $ | (15) |
根据式 (10)、(11)、(15) 可以求得考虑开洞影响后的侧板剪应变,与整板剪应变相比,可以得到相应的变形放大系数,其倒数为刚度折减系数,见式 (16)、(17).
加固处理的窗形开洞:
| $ {\kappa _{{\rm{c1}}}} = \frac{{{\gamma _{\rm{j}}} + {\gamma _{\rm{n}}}}}{{{\lambda _{\rm{j}}}{\gamma _{\rm{j}}} + {{\lambda '}_{\rm{n}}}{\gamma _{\rm{n}}}}} = \frac{{1 + \frac{{0.35{\varphi _{\rm{n}}}}}{{{H^2}{t^2}{\varphi _{\rm{j}}}}}}}{{{\lambda _{\rm{j}}} + {{\lambda '}_{\rm{n}}} \times \frac{{0.35{\varphi _{\rm{n}}}}}{{{H^2}{t^2}{\varphi _{\rm{j}}}}}}}. $ | (16) |
无加固处理的窗形开洞:
| $ {\kappa _{{\rm{c2}}}} = \frac{{{\gamma _{\rm{j}}} + {\gamma _{\rm{n}}}}}{{{\lambda _{\rm{j}}}{\gamma _{\rm{j}}} + {{\lambda '}_{\rm{n}}}{\gamma _{\rm{n}}}}} = \frac{{1 + \frac{{0.35{\varphi _{\rm{n}}}}}{{{H^2}{t^2}{\varphi _{\rm{j}}}}}}}{{{\lambda _{\rm{j}}} + {{\lambda '}_{\rm{n}}} \times \frac{{0.35{\varphi _{\rm{n}}}}}{{{H^2}{t^2}{\varphi _{\rm{j}}}}}}}. $ | (17) |
式中γj、γn分别是集装箱侧板由纯剪作用引起的剪应变、由扭曲作用引起的剪应变,按照整箱的理论进行计算.
2.2 门形洞口对于门形开洞,当洞口限制时,可以取a1、a2的和作为等效长度进行分析,取为等效长度之后仍按照整板进行计算.相应的折减系数计算公式为
| $ {\kappa _{\rm{m}}} = \frac{1}{{{\lambda _{\rm{m}}}}} = 1 - \frac{{{a_{\rm{h}}}}}{L}. $ | (18) |
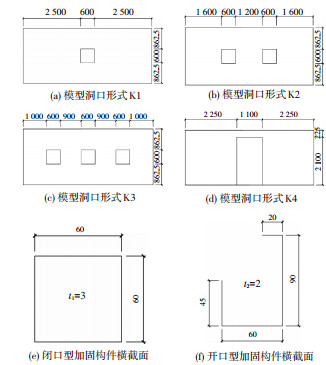
为验证理论,针对20 ft标准箱,设计如图 5所示的K1-K4共4种满足欧洲规范的开洞形式,分为洞口四周加固与不加固两种情况,分别利用ABAQUS进行有限元模拟.模型是对整个箱体空间建模,并非取一块侧板,但最终的有限元结果图,是取的单侧进行展示.这是由于洞口有透视作用,三维的有限元云图看起来非常混乱,难以辨识.而集装箱模型是对称的,两侧的结果相同,因此取单侧进行分析即可,便于观察.
|
图 5 有限元模型设计几何参数图 (mm) Figure 5 Geometric parameters of finite element model design (mm) |
模型尺寸根据规范取得,整箱一共包含14个部件:角件、前后角柱、上下侧梁、前后端梁、下横梁、底梁、顶板、侧板、端板、门,其中顶板、侧板、端板以及门这4个part采用壳单元,其余采用实体单元.各instance (实体) 之间均采用tie连接 (焊接).模型材料均为SPAH钢,密度7 800 kg/mm3,弹性模量取值206 kN/mm2,泊松比取0.3.在模型两根上侧梁上分别施加等效于100 kN合力的水平向均布荷载,如图 1所示的荷载形式,并将4个底部角件以及下侧梁、底部端梁一并固定,边界设置为encastre (固结).其中,加固构件选用方钢管,分为闭口型以及开口型两种,其横截面尺寸见图 5(e)、5(f).
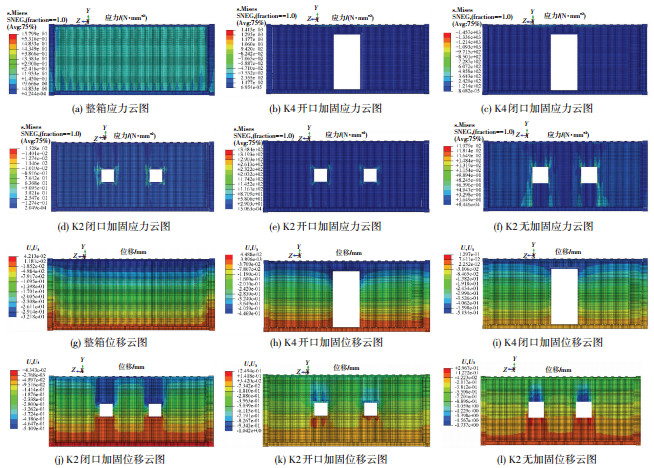
3.2 有限元模拟结果由于模拟的情况较多且篇幅有限,本文仅以K2、K4为例,输出相应的应力云图与位移云图进行分析,见图 6.抗侧刚度模拟值与理论值对比结果见表 1.
|
图 6 K2、K4开洞形式的有限元模拟云图 Figure 6 The finite element contour plots of K2 and K4 openings |
| 表 1 加固的窗形开洞模拟值与理论值对比 Table 1 Comparison between simulation and theoretical values of reinforced window openings |
从图 6可看出,加固处理的窗形洞口四周应力集中现象并不明显,侧移仍然分层均匀,仅在洞口上下边缘形成较大局部变形;而无加固洞口四周应力集中的范围明显更大,其洞口上下侧位移大于加固处理的情况,这同推导中扭曲变形放大的假设相吻合.对于门形开洞K4,其洞口两侧板块受力、位移均匀对称,近似于将作用力等分给了洞口两侧的板块,验证了理论假设.
由表 1可知,相较开口型加固,闭口型加固的抗侧刚度总是更大一些,与理论值更吻合,且随着洞口数增加,二者的差值加大,开口型加固的理论值与模拟值出现较大偏差.这是由于开口加固构件自身刚度小于闭口加固构件,说明加固构件本身的刚度对洞口加固的效果有影响.因此,本文的窗形开洞加固计算理论适用于边长60 mm,壁厚3 mm的方钢管加固件,而其他截面形式的加固件是否适用,还需要进一步验证.
对于无加固开洞,理论值与模拟值大致吻合,但误差相对闭口加固处理的情况较大,且K1时是负偏差,而到了K3则变成了正偏差.这是由于相对加固型开洞,未加固处理的开洞形式在洞口四周发生了更明显的应力集中,引起了相应的局部变形.由于洞口四周的应力集中受很多因素影响,推导中并未考虑,这对最终结果造成了一定的正偏差.然而,由于无加固开洞推导中附加扭曲效应采用了简化分析,本身带来了相应的负偏差,同应力集中造成的正偏差相抵消.对于K1一个开洞时,简化造成的负偏差更大,因此,总的偏差是负值.随着开洞面积的增大,应力集中造成的正偏差相比简化造成的负偏差增大速率更快,故而误差逐渐由负值变为正值.
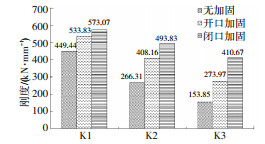
将K1~K3加固与不加固所对应的抗侧刚度拟合成柱状图进行对比,见图 7.对于满足开洞限制要求的三组模拟,无论是开口加固还是闭口加固,其对抗侧刚度的提升作用明显.并且,随着开洞面积比例的增大,加固的作用也越明显.因此,实际工程中应该考虑对洞口四周进行加固处理,加固构件应尽量选择闭口型加固构件.
|
图 7 窗形洞口不加固与加固的抗侧刚度对比 Figure 7 The comparison of the lateral stiffness of window openings with and without reinforcement |
1) 窗洞高度超限.实际工程中,如果窗洞超出限制,如开洞过高或者过宽,则开洞区域会形成很大的剪切变形突变,侧板两个方向的剪应变会产生较大差异,此时理论推导中认为开洞侧板剪切变形近似连续且两个方向剪应变相等的假设将不再成立.一般而言,集装箱的长度远大于高度,因而实际工程中窗洞多是高度无法满足限制.
2) 窗洞形状超限——圆形.不同于矩形洞口,圆形洞口在任意方向均完全对称,也不存在4个边角,因此圆形洞口四周的应力集中理论上应该小于同面积的矩形洞口,对抗侧刚度的折减应该更小.根据分析,做出以下假设:对于开洞形式满足窗洞限制的圆形开洞 (以其直径来判断),可将其等效为其内接正方形大小的矩形窗洞进行计算.
3) 门洞位置超限.对于门形开洞,针对高度与宽度的限制,在工程中相对容易满足,而洞口位置居中这一条则不易满足,因此针对门形开洞位置进行超出验证.
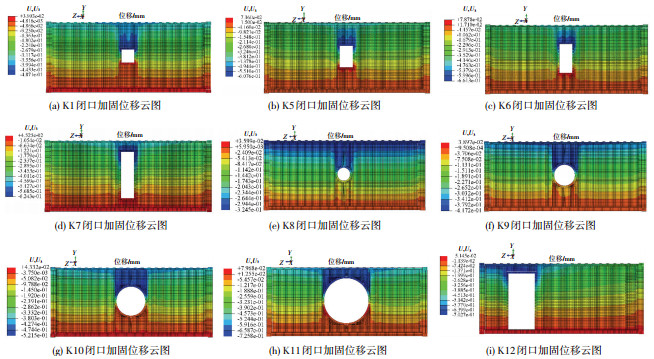
4.2 有限元模拟说明及结果为分析三种超限情况,针对20 ft标准箱,设计如图 8的K5~K7三种矩形窗洞形式,K8~K11四种圆形开洞形式,以及K12一种洞口偏置的形式.加固构件选用边长60 mm、壁厚3 mm的方钢管闭口型加固件,与洞口焊接连接.将K5~K7与K1进行对比,四者之间的区别仅仅在于洞口高度不同,分别为600、900、1 200、1 800 mm;将K8~K11进行对比,区别仅在于洞口直径不同,分别为600、900、1 200、1 800 mm;将K12与K4闭口加固进行对比,区别仅在于洞口位置不同,K12洞口距离左侧800 mm.同时,对圆形开洞,增设无加固处理组,验证计算理论.建立有限元模型的方法与第三节完全相同.位移云图见图 8,输出各组模拟的顶部角件侧移值,可以得到相应的抗侧刚度模拟值,将其与理论值进行对比,结果见表 2~4.
|
图 8 K1、K5~K12闭口加固开洞形式的有限元位移云图 Figure 8 The finite element deformation contour plots of openings with closed reinforcement |
| 表 2 高度超限的模拟值与理论值对比 Table 2 Comparison between simulation and theoretical values under the condition that height of openings exceeds the limit |
| 表 3 圆形开洞模拟值与理论值对比 Table 3 Comparison between simulation and theoretical values of circular openings |
| 表 4 K4与K12抗侧刚度的模拟值与理论值对比 Table 4 Comparison between simulation and theoretical values of the lateral stiffness of K4 and K12 |
从图 8可看出,K6、K7的高度相对K5增加明显,位移变化 (K7为0.408 mm、K6为0.39 mm、K5为0.372 mm) 却不大,这说明洞口达到一定高度后,该区域的蒙皮效应就几乎丧失,增加洞口的高度不会再对整体侧移产生明显影响.从表 2可看出,对于满足限制的K1,理论值同有限元值吻合较好;而对于超出限制的K5~K7,随洞口高度增加,理论值同模拟值的差距逐渐增大,计算理论不适用,这验证了理论假设以及计算式的适用范围.
根据图 8,圆形开洞的集装箱位移仍然大致均匀,仅在洞口上下侧形成局部突变,但突变范围小于方形洞口,这验证了假设分析.根据表 3,随着洞口尺寸的增大,理论值同模拟值的误差逐渐增大.这是由于直接将圆形洞口折减为内接方形洞口这种近似带来的负误差,这种误差随着面积的增大而增大.而且,这种近似对洞口无加固引起的附加扭曲效应的适应性较差,因此无加固开洞的误差较闭口加固开洞的误差更大.但K8除外,这是由于K8开洞面积很小,近似造成的负误差和应力集中造成的正误差刚好接近,因此有一部分抵消,以致其误差很小.但随着开洞面积的增大,这种近似方法所造成的误差增大的速率远高于应力集中所造成的正误差的增长率,因此不再能抵消,此时误差明显偏大.
对于内接方形洞口尺寸满足窗形洞口限制的圆形洞口 (K8、K9),其理论结果和模拟值较吻合,误差在可接受范围内,计算理论适用.而对于内接方形洞口尺寸超限的圆形洞口,则误差较大.这说明可用内接方形洞口的尺寸来限定圆形洞口,具体细则与窗形洞口相同.同时,可发现,当圆形洞口相较方形洞口面积更大时,其抗侧刚度值仍大于方形洞口.如 (K9与K1,K10与K2),这说明圆形洞口相较方形洞口更为有利.
根据图 8,K12门形开洞洞口两侧受力、位移不均匀,局部效应明显,其抗侧刚度也明显小于K4,这说明门形洞口对位置较为敏感.根据表 4,当门形位置超限时,集装箱左右两端角件处的侧移将明显不一致,离洞口近的一端,计算值与理论值产生很大偏差.
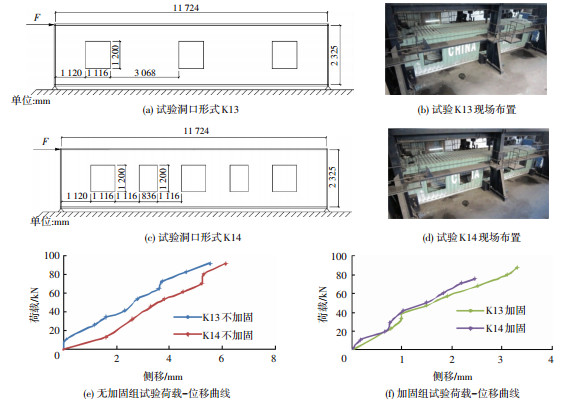
5 有限元方法的试验验证为研究开洞集装箱力学性能,针对40 ft标准箱进行过开洞试验,开洞形式K13、K14的具体几何参数以及现场布置见图 9(a)~(d).
|
图 9 K13、K14试验设计、布置和结果 Figure 9 Experiment design, layout and results of K13 and K14 |
每一种开洞形式,都分加固和非加固两组,加固构件为开口型加固构件,尺寸见图 5(f).试验得到的荷载位移曲线见图 9(e)、(f).基于试验,建立相应的有限元模型进行对比.有限元模型的建立同20箱相同,但加载方式有所区别——在模型加载端一侧的两个顶角件平行于端板的平面上分别施加等效于100 kN合力的水平向均布荷载.虽然试验的开洞形式、集装箱规格、加载方式同理论有所区别,但仍能借此验证集装箱开洞模型有限元建模方法的正确性,进而验证此前分析中用到的有限元模型.试验值与模拟值对比结果见表 5.可以看到试验值同模拟值吻合较好,有限元建模的方法得到了验证.
| 表 5 K13与K14抗侧刚度的模拟值与试验值对比 Table 5 Comparison between simulation and experimental values of the lateral stiffness of K13 and K14 |
1) 集装箱蒙皮效应对开洞敏感,基于欧洲蒙皮理论,分别从窗洞和门洞两方面对集装箱侧板开洞形式进行了规定,实际工程中集装箱开洞应尽量满足这些限制.
2) 针对满足限定的侧板开洞形式,推导得到了相应的抗侧刚度折减系数计算公式,并利用有限元模拟验证了理论,最后利用试验数据验证了有限元建模的方法,进而验证了有限元模型.
3) 通过有限元模拟对比了开口型加固、闭口型加固及无加固的情况,分析了加固作用以及加固构件对加固效果的影响,验证了理论适用范围.实际工程中窗洞应加固,加固件宜选边长60 mm、壁厚3 mm的方钢管.
4) 通过有限元模拟分析了窗洞高度、圆形开洞以及门洞位置这三种最常见的超限形式.结果表明圆形洞口相对方形洞口更为有利,应在实际工程中优先考虑,且验证了理论部分对窗洞高度以及门洞位置的限制.针对圆形开洞提出了相应的计算方法,并得到了验证.
5) 文中无加固的开洞集装箱抗侧刚度计算理论还不完善,无论是方形还是圆形,所采用的简化假设和近似方法考虑的因素较少,精度还不高,有待进一步研究.
致谢: 本论文得到深圳集装箱模块式房屋创意工程实验室 (批复号:深发改【2016】1444号) 项目的支持.| [1] | KOTNIK J. Container architecture[M]. Barcelona: Leading International Key Services Barcelona, 2013: 16-28. |
| [2] | SMITH J D. Shipping containers as building component[D]. Brighton: University of Brighton, 2005. |
| [3] | NELSON D. House, shipping container homes for beginners: how to live in a shipping container house[J]. Create Space Independent Publishing Platform, 2015, 86(3): 1356-1361. |
| [4] | GARRIDO L. Sustainable architecture containers[J]. Trans-Atlantic Publications, 2011, 45(3): 197-218. |
| [5] |
王明超. 集装箱式再生建筑空间设计研究[D]. 济南: 山东建筑大学, 2014.
WANG Mingchao. Study on the regeneration design of container construction space[D]. Jinan: ShandongJianzhu University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10430-1015516983.htm |
| [6] |
曾庆成, 孙丽敏, 杨忠振. 集装箱码头装卸混合调度模型[J].
哈尔滨工业大学学报, 2009, 41(10): 287-289.
ZENG Qingcheng, SUN Limin, YANG Zhongzhen. A scheduling model integrating loading and unloading operations at container terminals[J]. Journal of Harbin Institute of Technology, 2009, 41(10): 287-289. DOI: 10.3321/j.issn:0367-6234.2009.10.065 |
| [7] | GIRIUNAS K, SEZEN H, DUPAIX R B. Evaluation, modeling, and analysis of shipping container building structures[J]. Engineering Structures, 2012, 43: 48-57. DOI: 10.1016/j.engstruct.2012.05.001 |
| [8] | BØRVIK T, HANSSEN A G, DEY S, et al. On the ballistic and blast load response of a 20 ft ISO container protected with aluminium panels filled with a local mass-phase Ⅰ: design of protective system[J]. Engineering Structures, 2008, 30(6): 1605-1620. DOI: 10.1016/j.engstruct.2007.10.010 |
| [9] | AGUIAR D S, KIRKAYAK L, SUZUKI K, et al. Experimental and numerical analysis of container multiple stacks dynamics using a scaled model[J]. Ocean Engineering, 2013, 74: 218. DOI: 10.1016/j.oceaneng.2013.05.013 |
| [10] | KIRKAYAK L, SOUZA V, SUZUKI K, et al. On the vibrational characteristics of a two-tier scaled container stack[J]. Journal of Marine Science and Technology, 2011, 16(3): 354-365. DOI: 10.1007/s00773-011-0129-y |
| [11] |
王璐璐. 基于建筑和结构安全统一的废旧集装箱改造房构造的研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.
WANG Lulu. Study on construction of used shipping container buildings based on tne combination of architecture and structural security[D]. Harbin: Harbin Institute of Technology, 2010. http://www.doc88.com/p-7592991903108.html |
| [12] |
钟建伟. 集装箱模块化改造房力学性能的研究[D]. 哈尔滨: 哈尔滨工业大学, 2011.
ZHONG Jianwei. Research on mechanical properties of container modular transform house[D]. Harbin: Harbin Institute of Technology, 2011. |
| [13] |
曾毓鑫. 集装箱房抗侧及防火性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.
ZENG Yuxin. Research on lateral resistance and fire performance of container house[D]. Harbin: Harbin Institute of Technology, 2012. |
| [14] |
左洋, 查晓雄. 开洞集装箱房屋结构纵向刚度分析[J].
天津大学学报, 2015, 48(2): 167-176.
ZUO Yang, ZHA Xiaoxiong. Analysis of longitudinal stiffness of container building structure with holes[J]. Journal of Tianjin University, 2015, 48(2): 167-176. |
| [15] |
李英磊, 马荣奎, 李元齐. 集装箱模块化组合房屋单体纵向抗侧刚度及承载力数值分析[J].
建筑钢结构进展, 2014, 16(1): 28-33.
LI Yinglei, MA Rongkui, LI Yuanqi. Numerical analysis on longitudinal stiffness and ultimate strength of single container for modular freight container buildings[J]. Progress in Steel Building Structures, 2014, 16(1): 28-33. |
| [16] | ECCS. European recommendations for the stressed skin design of steel structures[S]. Croydon: European Convention for Constructional Steelwork, 1977: 56-58. |
| [17] | DAVIES J M, BRYAN E R. Manual of stressed skin diaphragm design[M]. Wiley: 1982: 89-93. |
| [18] | DAVIES J M. Light gauge steel diaphragms with openings[J]. IABSE Proceedings, 1978, 2(12): 755-768. |
 2017, Vol. 49
2017, Vol. 49


