2. 北京交通大学 土木建筑工程学院,北京100044
2. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China
近年来,随着不锈钢材料越来越得到建筑业的青睐[1-2],国外学者对不锈钢材料进行了深入研究,并修订了相关设计规范.Young等[3]对冷弯成型的不锈钢材料圆管柱进行了试件稳定试验研究,得到了局部屈曲、整体屈曲以及整体和局部的相关屈曲等失效模态,并结合试验数据评估了当前应用的规范设计公式; Gardner等[4-5]根据若干不锈钢试件的试验结果,总结并提出了连续强度法; Lui等[6]对冷弯双相型不锈钢构件进行试验研究并与美国规范、澳洲规范进行对比,认为两种规范的计算结果较保守; Hradil[7]研究了fy、n等材料特性对稳定性能的影响.
中国在不锈钢结构领域的研究尚处于起步阶段.王元清等[8-9]对焊接不锈钢梁的整体稳定性能进行了试验研究以及有限元分析,并在钢结构设计规范的基础上提出了修正建议公式; 郑宝峰[10]对冷弯薄壁不锈钢材料试件开展了轴心受压试验研究,并结合试验数据和有限元参数分析结果提出了不锈钢承载能力计算的建议公式; 此外,袁焕鑫[11]对焊接不锈钢轴心受压构件局部稳定和相关稳定性能进行了研究并给出了建议公式; 朱浩川[12]对薄壁不锈钢轴压构件进行了研究,基于有限元结果提出了不锈钢轴心受压构件的极限承载力计算方法.
本文使用经试验验证的有限元方法进行参数分析,根据参数分析结果提出不锈钢焊接箱形截面整体稳定系数的建议公式.
1 试验概况试验研究了6根双相型 (S2205) 与6根奥氏体型 (S304) 不锈钢焊接箱形截面轴压试件.所有构件的设计均经过了初算和数值模拟,以尽量确保试件在试验过程中发生整体失稳、避免发生局部屈曲.试验开始前,通过不锈钢材料性能试验得到了不锈钢在单向拉伸作用下轧制方向的材料属性.
试验过程中采用500T液压式长柱压力试验机进行加载,加载过程中,试件两端各布置一个单刀铰,使得加载装置与柱子端部实现单向铰接,单刀铰的转动轴线与试件弯曲失稳平面垂直.加载过程中使用位移计测量试件失稳平面内和平面外柱中截面的水平位移等.此外还对构件的荷载初偏心值和整体几何初始弯曲进行了测量[13].
2 有限元方法及试验验证 2.1 有限元模型 2.1.1 单元的选择及边界约束采用ANSYS12.0软件,选择Beam188单元建立几何模型,为模拟试验中构件两端的单刀铰,在模型中对相应的自由度进行释放.
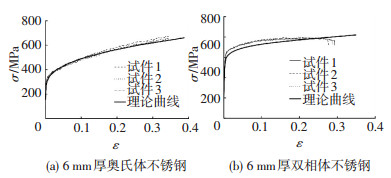
2.1.2 不锈钢材料的本构模型为使数值模拟能够更准确模拟试验,采用试验值的平均值作为理论曲线,见图 1.
|
图 1 应力-应变试验曲线与理论曲线的对比 Figure 1 Comparison of stress-strain curves of the tested coupons and the average value model curve |
在进行有限元模拟时可偏于安全地取一阶整体屈曲模态作为几何初始缺陷的变形状态,且为了准确起见,模型中几何初始缺陷应采用实测值.模型中通过对模型节点坐标进行更新,使实测几何初始缺陷作为模型的初始缺陷,模型见图 2.

|
图 2 初始几何缺陷模型 Figure 2 The initial geometric imperfection model |
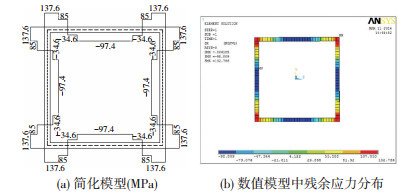
残余应力普遍存在于焊接构件中,且残余应力的存在会对构件的极限承载力产生影响,因此需要考虑残余应力对构件极限承载力的影响[14].有限元模型中采用袁焕鑫[11]测得的残余应力分布图,基于截面残余应力自平衡的理论对残余应力进行简化见图 3(a),将图 3(a)中的残余应力模型施加到构件中得到构件的残余应力分布见图 3(b).
|
图 3 残余应力分布 Figure 3 The distribution of residual stress |
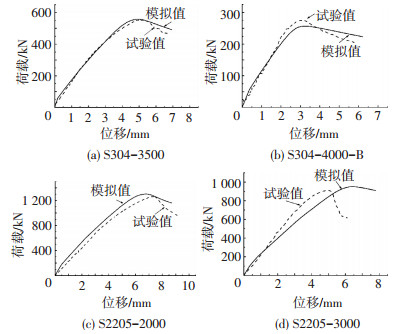
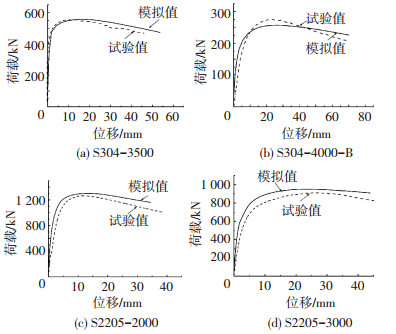
有限元模拟得到各构件的荷载与端部的竖向位移曲线与试验得到的荷载位移曲线的对比见图 4,模拟得到各构件的荷载与构件中点处水平位移曲线与试验得到的荷载位移曲线的对比见图 5.
|
图 4 竖向位移荷载曲线对比 Figure 4 Comparisons of load-vertical displacement |
|
图 5 横向位移荷载曲线对比 Figure 5 Comparisons of load-lateral displacement |
通过图 4、5可知,试验值与模拟值的荷载位移曲线匹配较好,有些荷载位移曲线存在一定的差异,例如初始缺陷较大的构件,这主要是由于构件初始缺陷是按构件最大初始缺陷的一阶模态来取用的,使得分析过于保守且与实际值存在差异.此外,单刀铰处的摩擦力以及构件的计算长度和残余应力模型简化也会对模拟产生影响.
2.2.2 极限荷载对比表 1列出了构件的几何参数及极限荷载值,其中B为构件截面的宽度;t为截面的厚度;Lt为钢柱两端单刀铰支座转动中心间距 (Lt=L+340) 即实际长度;e/Lt表示初始几何缺陷系数;使用欧洲不锈钢规范[15]计算得到构件的屈曲极限荷载值P1;使用美国不锈钢规范[16]计算得到构件的屈曲极限荷载值P2;构件的屈曲极限荷载试验值Pt;考虑残余应力时构件的屈曲极限荷载的有限元模拟值Py.
| 表 1 极限荷载对比 Table 1 Comparison of ultimate load |
通过对比极限屈曲荷载的有限元和试验结果,可知有限元模拟值与试验值的误差在10%以内,平均误差在5%之内.误差在可接受范围内,进一步验证了有限元方法的可行性.
3 参数分析使用以上经试验验证的有限元方法,进行参数化分析.有限元模型中几何初始缺陷采用0.001L,截面残余应力采用袁焕鑫[11]提出的残余应力模型,材料力学性能采用试验数据,截面宽厚比的选取与试验构件相同.分别讨论构件几何初始缺陷、截面残余应力、材料力学性能、截面宽厚比以及长细比对构件极限承载性能的影响.
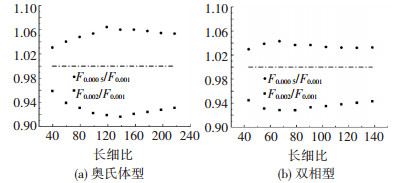
3.1 构件几何初始缺陷本文选取初始缺陷值为0.000 5L、0.001L、0.002L的3种情况进行有限元分析,并将极限荷载值F0.000 5、F0.002与极限荷载值F0.001进行对比,见图 6.图中纵坐标表示极限荷载F0.002、F0.000 5与极限荷载F0.001的比值.
|
图 6 初始缺陷的影响 Figure 6 The influence of initial defects |
通过对比不同初始缺陷值对不锈钢箱形构件极限荷载的影响可知:初始缺陷为0.000 5L时的极限荷载比初始缺陷为0.001L的极限荷载高约5%,初始缺陷为0.002的极限荷载比初始缺陷为0.001的极限荷载低约7%,且均随长细比变化轻微波动;奥氏体与双相型对比可知不同初始缺陷对两者影响规律基本相同,但初始缺陷对双相型构件极限荷载影响较小.
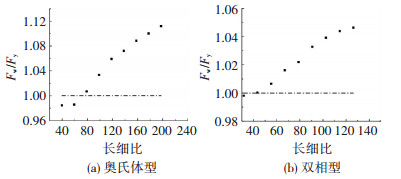
3.2 构件截面残余应力的影响分别对考虑残余应力与不考虑残余应力两种情况进行有限元分析,并将两者的极限荷载值进行对比,见图 7.图中纵坐标表示不考虑残余应力时构件的极限荷载Fw与考虑残余应力的极限荷载Fy的比值.
|
图 7 残余应力的影响 Figure 7 The influence of residual stress |
通过对比可知:随长细比增大,残余应力对构件的极限承载力影响增大;奥氏体与双相型对比可知残余应力对两者的影响规律基本相同,但残余应力对双相型构件极限荷载影响较小.
3.3 材料力学性能的影响试验过程中分别针对两种不同种类以及两种不同厚度的不锈钢材料进行材性试验,得到的材料属性见表 2.
| 表 2 轧制方向材料属性 Table 2 Material properties of rolling direction |
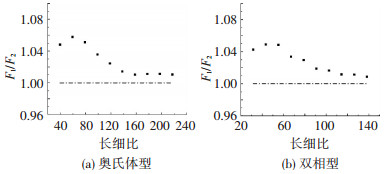
分别取用不同厚度的奥氏体和双相型不锈钢测得的材料特性曲线进行有限元分析,并对有限元模拟得到的极限荷载进行对比,见图 8.图中纵坐标表示两种不同材料特性不锈钢构件极限荷载F1、F2的比值.通过对比可看出:长细比较小时材料力学性能对构件极限荷载影响较大;奥氏体与双相型对比可知材料力学特性对两者的影响规律基本相同,但对双相型构件极限荷载影响较小.
|
图 8 材料力学特性的影响 Figure 8 The influence of material mechanical properties |
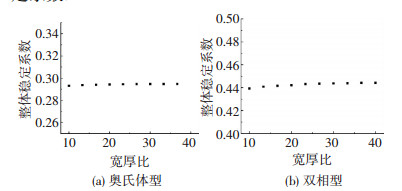
通过改变截面宽厚比,使用有限元分析获得极限荷载并对比按照中国钢结构规范计算得到的稳定系数的变化,见图 9.图中纵坐标表示构件的整体稳定系数.
|
图 9 宽厚比的影响 Figure 9 The influence of width-to-thickness ratio |
宽厚比对构件极限承载力的影响较小,分析时可忽略;截面宽厚比对奥氏体与双相型构件极限承载力的影响规律基本相同.
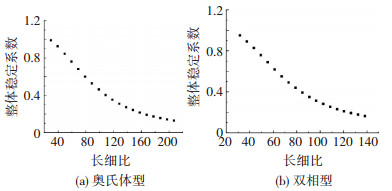
3.5 构件长细比的影响改变构件的长度来改变构件的长细比,通过有限元分析确定当构件长细比改变时构件极限荷载的变化,见图 10.图中纵坐标表示构件按照中国钢结构规范计算得到的整体稳定系数.
|
图 10 长细比的影响 Figure 10 The influence of slenderness ratio |
奥氏体型与双相型不锈钢的极限荷载随长细比的变化均呈现出较明显改变,构件长细比越大极限荷载值越小;构件长细比对奥氏体型与双相型构件极限承载力的影响规律基本相同.
通过影响因素的讨论可知构件的长细比对构件极限承载力的影响占主导作用,截面的宽厚比 (尺寸) 对构件极限承载力几乎无影响,残余应力、初始几何缺陷以及材料特性均会对构件的极限承载力产生一定影响.此外,截面残余应力分布已通过试验测得,几何初弯曲通过统计可得到确切值,材料特性可通过引入正则化长细比的概念进行考虑,因此主要探讨构件长细比对构件极限承载力的影响.
4 计算方法 4.1 计算方法提出目前针对不锈钢设计常用的规范有欧洲规范与美国规范,其中欧洲规范在设计时考虑了构件的初始缺陷等问题,但对于材料的非线性只是在系数中进行了考虑.而美国规范中采用切线模量的方法对材料的非线性进行了考虑,但对于构件的初始缺陷只是简单进行了折减.通过表 1对比并结合各规范的设计方法对构件极限荷载计算方法进行建议,当构件长细比较大时可采用欧洲不锈钢计算形式,当构件长细比较小时可采用美国不锈钢计算形式.
本文将柱子曲线分为三段分别进行计算.第一段,由于正则化长细比较小,构件失稳时由于截面屈服应力已超过fy,边缘屈服准则已不再成立,因此对于此类问题可采用Gardner[4]提出的连续强度法.由于此种方法计算比较复杂且实际中此类长细比较小的构件较少,因此为了使用方便以及曲线的完整可采用一段保守的函数曲线来代替.第二段,考虑到材料的非线性特性,构件失稳形式为弹塑性失稳,综合美国钢结构规范以及冷弯构件的直接强度法,可采用美国冷弯不锈钢规范中给出的公式形式.第三段,此时构件正则化长细比较大,构件失稳形式为弹性失稳,可采用基于构件边缘屈服准则提出的perry公式的形式:
| $ \varphi = \left\{ \begin{array}{l} {a_1} + {a_2}*{\lambda ^2}, \lambda \le a;\\ {a_3}*a_4^{{\lambda ^2}}, a < \lambda \le b;\\ \frac{1}{{2{\lambda ^2}}}\sqrt {\left( {{a_5} + {a_6}\lambda + {\lambda ^2}} \right)- \left[{\left( {{a_5} + {a_6}\lambda + {\lambda ^2}} \right){^2}-4{\lambda ^2}} \right]} {\rm{ }}, b < \lambda . \end{array} \right. $ |
对于两个分界点a、b,第一个分界点a可根据美国不锈钢规范中构件失稳时对应的应力σ达到截面屈服应力fy时来确定,即满足:
| $ \sigma = \frac{{{{\rm{\pi }}^2}{E_{\rm{t}}}}}{{{{\left( {KL/r} \right)}^2}}} = \frac{{{{\rm{\pi }}^2}}}{{{{\left( {KL/r} \right)}^2}}} \times {\rm{ }}\frac{{{E_0}{f_{\rm{y}}}}}{{{f_{\rm{y}}} + 0.002n{E_0}{{\left( {\frac{\sigma }{{{f_{\rm{y}}}}}} \right)}^{n-1}}}}, $ |
σ=fy时对应的长细比为
| $ {\left( {KL/r} \right)^2} = \frac{{{{\rm{\pi }}^2}{E_0}}}{{{f_{\rm{y}}} + 0.002n{E_0}}}. $ |
式中:Et表示材料的切线弹性模量,E0表示材料的初始弹性模量,n为材料的硬化系数.
通过计算以及考虑到数据的简便性,对于奥氏体型的第一分界点a可取0.25,双相型的第一分界点a可取0.4.对于第二个分界点b,由于不锈钢的弹塑性失稳与弹性失稳之间没有明确界定,可通过拟合方法获得.
4.2 数据拟合通过对奥氏体型与双相型不锈钢进行参数化有限元分析,将得到的有限元参数分析结果使用MATLAB根据提出的稳定系数公式进行拟合,通过拟合最终确定公式中系数的取值,并考虑到系数的简便以及曲线的连续性对系数进行简单处理见表 3.
| 表 3 系数取值 Table 3 Coefficient value |
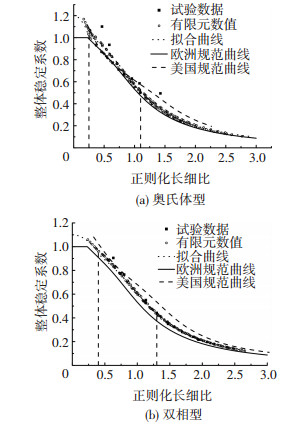
将拟合得到的曲线与有限元数值、试验数值、美国不锈钢规范中柱子曲线以及欧洲不锈钢规范中柱子曲线进行对比见图 11.
|
图 11 拟合曲线 Figure 11 Fitting curve |
由图 11可知,对于奥氏体型箱形构件,计算得到的柱子曲线高于欧洲不锈钢柱子曲线,且正则化长细比越大两者的差别越小,当正则化长细比较小时,计算得到的柱子曲线高于美国不锈钢柱子曲线,当正则化长细比较大时,计算得到的柱子曲线低于美国不锈钢柱子曲线;对于双相型箱形构件,计算得到的柱子曲线高于欧洲不锈钢柱子曲线,且正则化长细比越大两者差别越小,计算得到的柱子曲线低于美国不锈钢柱子曲线.当正则化长细比较小时柱子曲线与美国不锈钢钢柱子曲线间的差距较小,当正则化长细比较大时计算得到的柱子曲线与欧洲不锈钢钢柱子曲线间的差距较小.
本文提出的三段式适用于奥氏体型和双相型两类不锈钢构件.模拟值明显高于欧洲不锈钢柱子曲线,表明欧洲不锈钢规范较保守,模拟值与美国不锈钢规范曲线差别较大,表明美国不锈钢规范不适用于焊接不锈钢构件.三段式与试验以及有限元数据点的分布形态吻合较好,箱形截面构件的承载力计算值与试验以及有限元的平均比值均近似为1,表明三段式能够对奥氏体型、双相型不锈钢的箱形截面构件的整体稳定承载力进行合理计算.
5 结论1) 通过参数分析可确定构件几何初始缺陷、截面残余应力、材料力学性能、截面宽厚比以及长细比对构件的整体稳定承载力有影响,其中材料力学特性与长细比占主导作用.
2) 通过试验结果、有限元分析结果与欧洲不锈钢规范和美国不锈钢规范对比可得到欧洲不锈钢规范对于构件整体稳定性能的预测较保守,美国不锈钢规范不适用于焊接不锈钢构件.
3) 根据箱形不锈钢轴压构件的参数分析得到的结果提出了整体稳定系数的三段建议公式,该公式可很好地预测不锈钢构件的极限承载力.
| [1] |
王元清, 袁焕鑫, 石永久, 等. 不锈钢结构及其应用和研究现状[J].
钢结构, 2012(2): 1-13.
WANG Yuanqing, YUAN Huanxin, SHI Yongjiu, et al. A review of current applications and research of stainless steel structure[J]. Steel Structure, 2012(2): 1-13. |
| [2] | GARDNER L. The use of stainless steel in structures[J]. Progress in Structural Engineering Materials, 2005(7): 45-55. |
| [3] | YOUNG B, HARTONO W. Compression tests of stainless steel tubular members[J]. Journal of Structural Engineering, 2002, 128(6): 754-761. DOI: 10.1061/(ASCE)0733-9445(2002)128:6(754) |
| [4] | GARDNER L. The continuous strength method[J]. Structures & Buildings, 2008, 161(SB3): 127-133. |
| [5] | GARDNER L, THEOFANOUS M. Discrete and continuous treatment of local buckling in stainless steel elements[J]. Journal of Constructional Steel Research, 2008, 64(11): 1207-1216. DOI: 10.1016/j.jcsr.2008.07.003 |
| [6] | LUI W M. Tests of cold-formed duplex stainless steel SHS beam-columns[J]. Engineering Structures, 2014, 74: 111-121. DOI: 10.1016/j.engstruct.2014.05.009 |
| [7] | HRADIL P. Numerical verification of stainless steel overall buckling curves[J]. Thin-Walled Structures, 2014, 83: 52-58. DOI: 10.1016/j.tws.2014.01.011 |
| [8] |
王元清, 高博, 戴国欣, 等. 焊接不锈钢工字形截面梁整体稳定性试验研究[J].
建筑结构学报, 2011, 32(11): 143-148.
WANG Yuanqing, GAO Bo, DAI Guoxin, et al. Experimental study on lateral buckling behavior of stainless steel beams with welded Ⅰ-sections[J]. Journal of Building Structures, 2011, 32(11): 143-148. |
| [9] |
王元清, 高博, 戴国欣, 等. 焊接工字形截面不锈钢受弯构件的整体稳定性分析[J].
沈阳建筑大学学报 (自然科学版), 2010, 26(6): 1021-1026.
WANG Yuanqing, GAO Bo, DAI Guoxin, et al. Analysis on overall stability of stainless steel beams with welded i-section[J]. Journal of Shenyang Jianzhu University (Natural Science), 2010, 26(6): 1021-1026. |
| [10] |
郑宝峰. 不锈钢冷弯薄壁型钢轴心受压和受弯构件理论分析与试验研究[D]. 南京: 东南大学, 2010.
ZHENG Baofeng. Stainless steel cold bending thin-wall steel axial compression and flexural member of theoretical analysis and experimental research[D].Nan Jing: University of Nan Jing, 2010. |
| [11] |
袁焕鑫. 焊接不锈钢轴心受压构件局部稳定和相关稳定性能研究[D]. 北京: 清华大学, 2014.
YUAN Huanxin. Local and local-overall buckling behaviour of welded stainless steel member under axial compression[D]. Beijing: Tsinghua University, 2014. |
| [12] |
朱浩川. 薄壁不锈钢轴压构件的极限承载力[D]. 杭州: 浙江大学, 2014.
ZHU Haochuan. Ultimate bearing capacity of thin-walled stainless steel members in axial compression[D]. Hangzhou: Zhejiang University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10335-1014171316.htm |
| [13] |
杨璐, 徐东辰, 王元清, 等. 奥氏体型不锈钢焊接箱形截面轴压构件整体稳定性能试验研究[J].
土木工程学报, 2014, 47(2): 83-88.
YANG Lu, XU Dongchen, WANG Yuanqing, et al. Experimental study on the overall buckling behavior of austenitic stainless steel columns under axial compression[J]. China Civil Engineering Journal, 2014, 47(2): 83-88. |
| [14] |
张壮南, 张耀春. 残余应力对单轴对称工字梁稳定承载力的影响[J].
哈尔滨工业大学学报, 2007, 39(12): 1864-1868.
ZHANG Zhuangnan, ZHANG Yaochun. Effects of welding residual stresses on the stability capacity of the monosymmetric Ⅰ-beams[J]. Journal of Harbin Institute of Technology, 2007, 39(12): 1864-1868. DOI: 10.3321/j.issn:0367-6234.2007.12.004 |
| [15] | Eurocode3: Design of steel structures-part 1.4: general rules supplementary rules for stainless steels:EN1993-1-4[S]. Brussels: European Committee for Standardization (CEN), 2006. |
| [16] | Specification for the design of cold-formed stainless steel structural members: SEI/ASCE 8-02[S].New York: American Society of Civil Engineers, 2002. |
 2017, Vol. 49
2017, Vol. 49


