2. 哈尔滨工业大学 土木工程学院,哈尔滨 150090
2. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China
在建筑结构的适当部位安装耗能减震元件以减小地震或风振作用越来越常见.耗能器可分为位移型和速度型两种.位移型耗能器设置于结构中,既可以是抗侧力构件的组成部分,也可以在大震下屈服耗能,耗散部分输入上部结构的地震能量,主体结构储存和耗散的地震能量相应减小从而更安全.近些年,各种用于结构减振的性能优良的位移型耗能器被开发出来[1-6].Chan等[1]开发了一种带切口的钢板阻尼器,对其进行了性能试验,研究了其几何参数的影响;Vargas等[2]对一安装有金属阻尼器和粘滞阻尼器的单自由度体系进行了减震参数研究;Li等[3]对不同开口形状的钢板阻尼器进行了缩尺和足尺性能试验,建立多层结构三维有限元模型,利用该阻尼器进行减震动力反应分析;王铁英等[4]设计了一种钢铅组合耗能器用于具有竖向耗能能力的抗倾覆装置中,通过试验及理论分析给出了耗能器的力学性能和恢复力模型;辛亚军等[5-6]对一种低屈服极限新型钢铅组合耗能器进行了性能试验及减震体系仿真分析,卢德辉等[7-8]对一种中部削弱钢管铅芯阻尼器进行了几何参数影响分析和单层单榀偏心支撑框架的有限元拟静力位移加载分析.
由于地震动的多维特性,结构可能在任何方向产生变形,因此要求设置在结构中的耗能器也能具有多向耗能能力.颜学渊等[9-11]和程树良等[12]对一种具有水平双向耗能能力的工字型新型钢铅组合耗能器 (CSLD) 的力学性能进行了试验和数值模拟,并对其进行参数优化,将其安装在单层钢框架结构模型层间进行地震模拟振动台试验,研究了其耗能减震效果.但是,这种钢铅组合耗能器也因设计成工字型,外部激励作用下,在直角区域的不锈钢和铅芯容易应力集中,容易过早屈服断裂退出工作 (特别是翼缘部分的不锈钢),从而构件性能降低.针对这个问题,本文提出一种加工简便,水平两个方向都具有良好耗能性能的椭圆形截面钢铅耗能器,该耗能器已申请国家专利[13].本文将对这种耗能器进行平面应力分析;对不同尺寸的耗能器进行力学性能试验,应用ANSYS软件对耗能器进行精细化建模分析并与性能试验结果进行对比;通过振动台试验探讨其对多层钢框架结构的振动控制效果.
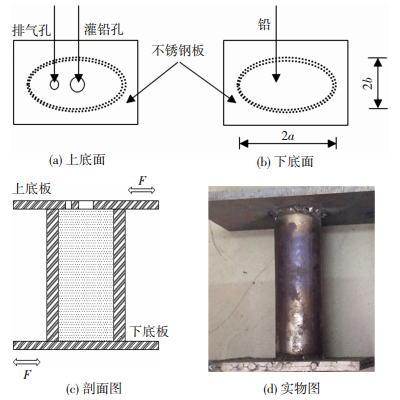
1 椭圆形钢铅耗能器简介如图 1所示,椭圆形钢铅耗能器包括上底板、下底板、椭圆形不锈钢管和铅芯,上底板设有灌铅孔和排气孔,不锈钢管由不锈钢板卷曲焊接而成,再用氩弧焊焊接在上下底板上.椭圆形钢铅耗能器具有较大的水平初始刚度和较低的水平屈服力,但其竖向承载力也较小,可以安装在有发生相对变形的结构或桥梁等上面,在受到剪力作用时,利用上底板和下底板之间的相对剪切变形耗散能量,达到消能减震的目的.椭圆形钢铅耗能器水平两个方向都具有耗能能力,可根据实际需要设计耗能器的长短轴长度、钢管壁厚及耗能器高度.
|
图 1 椭圆形钢铅耗能器构造示意 Figure 1 Constitution figure of OSLD |
椭圆形钢铅耗能器铅芯与钢板的相互作用可按平面应力来考虑,椭圆的长轴长为2a,短轴长为2b,取单位高度的试件进行分析.
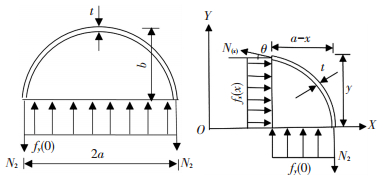
根据图 2左图所取的半截面椭圆形隔离体,由Y轴静力平衡有:
| $\sum {{F_y} = 0 \Rightarrow 2{N_2} - {f_y}\left( 0 \right)2a = 0.} $ | (1) |
取图 2右图所示椭圆形钢铅耗能器隔离体,由静力平衡有:
| $\left( {a-x} \right){f_y}\left( 0 \right) + {N_{\left( x \right)}}\sin \theta-{N_2} = 0.$ | (2) |
式中:fy(0) 为铅芯受到的在纵坐标为0时候的竖向压力,N(x)为薄钢板受到的在横坐标为x(纵坐标y) 处的环向拉力,N2为不锈钢管受到的在x=a处的环向拉力,θ为N(x)与水平方向的夹角.
|
图 2 椭圆形钢铅耗能器隔离体 Figure 2 Free body diagram of OSLD |
对椭圆方程在 (x, y) 点处求导可得
| $\tan \theta = \frac{{bx/{a^2}}}{{\sqrt {1-{{\left( {x/a} \right)}^2}} }}.$ | (3) |
联立式 (1)~(3) 及椭圆方程可解得
| ${N_{\left( x \right)}} = \sqrt {\frac{{{a^2}-{x^2}}}{{{b^2}}} + \frac{{{x^2}}}{{{a^2}}}} {N_2}.$ | (4) |
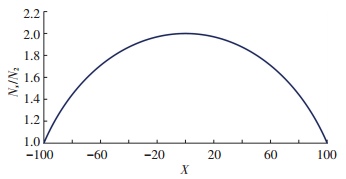
假定椭圆长轴半径a=100,短轴半径b=50,则可以得到薄钢板所受到拉应力的分布图,见图 3.从图 3可看出,椭圆形钢铅耗能器中薄钢板拉应力沿X轴呈抛物线分布,在椭圆薄钢板短轴处拉应力值最大,在椭圆薄钢板长轴两端的拉应力值最小;因此在实际制作耗能器时,椭圆薄钢板的焊接部位应远离轴线位置.
|
图 3 薄钢板拉应力沿X轴分布 Figure 3 Stress distribution of steel plate in X direction |
为了分析椭圆形钢铅耗能器的力学性能,加工如表 1所示的4个试件.
| 表 1 试件尺寸 Table 1 Geometry parameters of OSLD specimens |
试验的加载装置采用MTS试验机,为了便于加载,所制作的试件都加工成双剪切的形式[4],见图 4(a).椭圆形钢铅耗能器是一种位移相关型耗能器,加载的速率对于耗能器性能影响小,因此结合现有的加载装置,对耗能器采取了加载频率为0.5 Hz的往复加载试验.试验采用位移控制,对试件施加长轴方向的正弦波往复荷载,分4个加载等级进行加载,加载位移±1 mm、±3 mm、±5 mm、±10 mm循环3周,主控计算机自动记录试验的数据.

|
图 4 耗能器破坏模式 Figure 4 Failure mode of OSLD |
观察试验可发现,椭圆形钢铅耗能器的破坏大体可分为3个阶段:初始加载阶段,耗能器外观基本没有变化,力与变形关系处于弹性阶段;随着位移进一步增大,加载荷载超过耗能器的屈服荷载,耗能器进入塑性变形阶段,可以看到外包薄钢板出现屈曲 (图 4(b)),虽然钢板和内部铅屈服,但是试件的承载力还有一定的增长,因为薄钢板屈曲产生微小平面位移会在薄钢板上产生薄膜拉应力[14];对耗能器进行大位移破坏性试验时,在靠近底板焊接部位的薄钢管出现剪切破坏 (图 4(c)),试件1薄钢管在加载位移为22.6 mm时出现剪切破坏.
在所制作的4个试件中,试件3薄钢管焊接成型的位置在轴线处,在对试件3进行破坏性试验时,薄钢管未被剪断的时候就已经在焊接的部位出现开口裂缝 (图 4(d));而试件1的焊接部位远离椭圆柱短轴线 (也不位于长轴线处),进行破坏试验时,耗能器的薄钢管被剪断时,薄钢管焊接成型的部位未出现裂缝.这一现象进一步验证了上一节的平面内应力分析结果,椭圆薄钢管在加工焊接时,其焊接的部位应该远离椭圆柱轴线.在实际工程应用椭圆形钢铅耗能器进行减震时,制作椭圆薄钢管应该尽量采用一体化成型,从而避免椭圆薄钢管因焊接而出现薄弱位置.
4个椭圆形钢铅耗能器的力与变形关系曲线见图 5,滞回曲线饱满,表明椭圆形钢铅耗能器具有较强的耗能能力;曲线形状接近平行四边形,因此可以将其力学模型简化为双线性.此外,还另加工了8个尺寸相同的椭圆形钢铅耗能器,其钢板厚度为1.0 mm,短轴长20 mm,长轴长30 mm,高度为200 mm.取其中的两个试件分别进行长轴向和短轴向的力学性能试验,其力与位移关系曲线见图 6,其余6个试件用于后文的振动台试验.将图 6中的曲线简化为双线性,可得到其长轴向的力学参数:屈服强度Fy为13.6 kN, 弹性刚度K1为9.6 kN/mm和屈服后刚度比K2/K1为9.1%;短轴向的力学参数:屈服强度Fy为10.2 kN, 弹性刚度K1为5.7 kN/mm和屈服后刚度比K2/K1为10.5%.

|
图 5 有限元分析与试验结果对比 Figure 5 Comparison of numerical analyses and tests |

|
图 6 椭圆形钢铅耗能器力与位移关系曲线 Figure 6 Force-displacement relationship of OSLD |
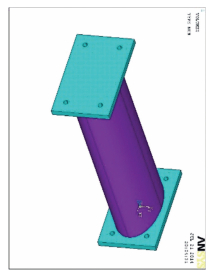
利用有限元分析软件ANSYS建立椭圆形钢铅耗能器的实体模型,外部不锈钢薄钢管用壳单元SHELL181模拟;内部铅芯用三维实体单元SOLID45模拟;铅与不锈钢的接触为面面接触,不锈钢管单元面指定为目标面,用目标单元TARGE170模拟,铅单元面指定为接触面,用接触单元CONTA173模拟.选定单元后,定义材料参数,建立模型并进行网格划分,图 7为椭圆形钢铅耗能器的有限元模型.根据不锈钢与铅的材料特性,二者的力学模型均采用双线性随动强化模型 (BKIN).主要材料参数如下:不锈钢的弹性模量为118.4 GPa,屈服强度为225 MPa,泊松比取0.3;铅的弹性模量为16.5 GPa,屈服强度为7.5 MPa,泊松比取0.44.在加载分析时,固定耗能器的下底板,而给上底板X向 (长轴方向) 施加往复位移荷载步,施加的位移与试验一致,数值分析结果见图 5.从图 5可看出,试验和ANSYS数值分析的力与位移关系曲线吻合很好,所建立的有限元模型可以较好模拟椭圆形钢铅耗能器.
|
图 7 耗能器有限元模型 Figure 7 Numerical model of OSLD |
在理论分析与性能试验研究的基础上,为实际检验椭圆形钢铅耗能器对多层建筑结构水平双向地震反应的控制效果,设计制作一个6层钢框架结构模型,将前述椭圆形钢铅耗能器安装在模型每一层上,形成耗能结构体系.对耗能结构体系进行地震模拟振动台试验,并与同一模型的不安装椭圆形钢铅耗能器的结构体系进行试验对比, 见图 8.结构模型平面尺寸为1.6 m×0.8 m,层高0.8 m.模型结构主梁采用80×43×5槽钢,次梁采用50×37×4.5槽钢,柱子采用L80×7等肢角钢,梁柱节点为刚性连接.包括支撑在内的结构模型自重为1.57 t,模型每层加人工配重1.3 t,结构模型的总重量为10.67 t.椭圆形钢铅耗能器安装于层间,长轴向与模型结构长跨方向 (Y向) 重合.

|
图 8 结构模型 Figure 8 Structure model |
在结构模型的各层及振动台台面均布置了加速度和位移传感器以量测结构的地震反应.分别对有安装耗能器 (有控结构) 和不安装耗能器 (无控结构) 的两个结构模型输入峰值为220 gal的天津波 (NS分量) 和上海人工波,分长跨方向和短跨方向输入.白噪声扫频工况获得无控结构的X向和Y向基本周期为0.403 s和0.471 s,有控结构为0.370 s和0.264 s.
布置在台面的加速度传感器显示其数值与预期的220 gal输入有差别,但相差较小,为反映减震效果,定义椭圆形钢铅耗能器对结构模型的地震反应控制效果为
| $C = \frac{{{R_{\rm{u}}}/{I_{\rm{u}}}-{R_{\rm{c}}}/{I_{\rm{c}}}}}{{{R_{\rm{u}}}/{I_{\rm{u}}}}} \times 100\%, $ | (5) |
式中:C为控制效果,Ru为结构无控反应,Rc为结构有控反应,Iu为无控台面实际输入,Ic为有控台面实际输入.
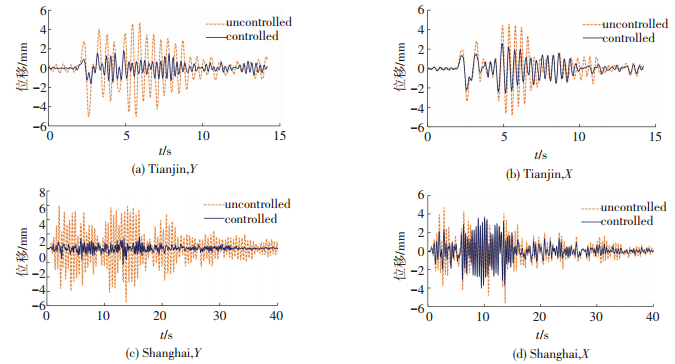
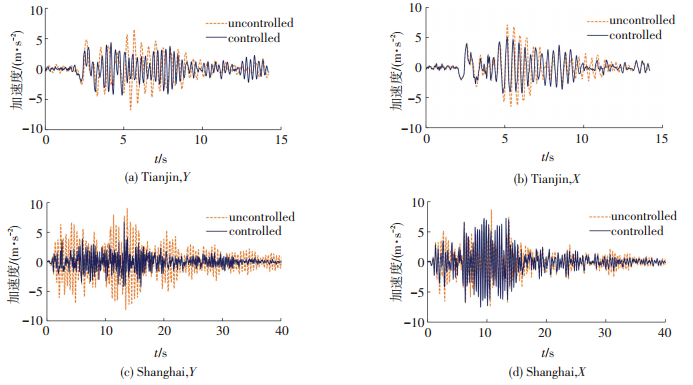
表 2、3所示为在两条不同地震动作用下,结构各楼层不同方向的层间位移和加速度反应及控制效果.图 9、10分别为部分结构底层层间位移反应时程曲线和顶层加速度反应时程曲线.
| 表 2 结构层间位移反应及控制效果 Table 2 Structural inter-story displacement responses and control effects |
| 表 3 结构加速度反应及控制效果 Table 3 Structural acceleration responses and control effects |
|
图 9 结构底层层间位移反应时程曲线 Figure 9 `Inter-story displacement time histories of bottom layer |
|
图 10 结构顶层加速度反应时程曲线 Figure 10 Acceleration time histories of top layer |
从表 2、3和图 9、10可看出,模型结构安装椭圆形钢铅耗能器可以较好控制结构的地震反应.大震作用下,耗能器进入屈服,消耗部分地震能量,有控结构各层的位移和加速度反应大部分比无控结构来的小,特别是层间位移控制效果较明显;但是由于耗能器也附加给结构一定的刚度,在一些楼层及某些时刻,结构的加速度反应仍较大,有时甚至会有略微放大.椭圆形钢铅耗能器具有水平双向的耗能减震功能,对结构不同方向的地震反应都有减震控制效果;对本模型结构而言,Y向 (长跨) 的减震效果要好于X向,主要是由于阻尼器参数设置不够优化.不同特性地震动作用下,不同楼层的地震响应减震效果有差异,天津波作用下的减震效果一般要好于上海人工波.陈宏[15]研究表明当屈服比 (椭圆形钢铅耗能器屈服力与框架结构楼层的屈服力比值) 为6.3%的时候,地震动作用下椭圆形钢铅耗能器对结构位移和加速度的控制效果都会比较好;而本文X向和Y向的屈服比为10.3%和13.8%,比较大,因此,其对结构地震反应的控制效果略差一些,但可通过耗能结构的优化设计达到更理想的减震效果.
5 结论本文提出一种椭圆形钢铅耗能器,对其进行了数值分析和性能试验;将其安装于一个6层钢框架结构模型上,进行了振动台减震试验.得到如下结论:
1) 椭圆形钢铅耗能器的力与变形关系曲线形状接近平行四边形,可以将其力学模型简化为双线性;其滞回曲线饱满,表明椭圆形钢铅耗能器具有较强的耗能能力.
2) 理论分析与性能试验表明,制作椭圆薄钢管应该尽量采用一体化成型或者避开轴线位置进行焊接,以避免焊缝率先开裂.
3) 性能试验和ANSYS数值分析的力与位移关系曲线吻合很好,所建立的有限元模型可以较好模拟椭圆形钢铅耗能器.
4) 振动台试验结果表明椭圆形钢铅耗能器对多层结构的地震响应有较好控制效果.
| [1] | CHAN R W K, ALBERMANI F. Experimental study of steel slit damper for passive energy dissipation[J]. Engineering Structures, 2008, 30(4): 1058-1066. DOI: 10.1016/j.engstruct.2007.07.005 |
| [2] | VARGAS R, BRUNEAU M. Effect of supplemental viscous damping on the seismic response of structural systems with metallic dampers[J]. Journal of Structural Engineering, 2007, 133(10): 1434-1444. DOI: 10.1061/(asce)0733-9445(2007)133:10(1434) |
| [3] | LI G, LI H N. Experimental study and application in steel structure of 'dual functions' metallic damper[J]. Advanced Steel Construction, 2013, 9(3): 247-258. DOI: 10.18057/ijasc.2013.9.3.6 |
| [4] |
王铁英, 王艳武, 王焕定, 等. 钢铅组合耗能器力学性能试验研究[J].
工程力学, 2005, 22(2): 149-154.
WANG Tieying, WANG Yanwu, WANG Huanding, et al. Experimental study of mechanical properties of steel-lead mixed dampers[J]. Engineering Mechanics, 2005, 22(2): 149-154. DOI: 10.3969/j.issn.1000-4750.2005.02.027 |
| [5] |
辛亚军, 王焕定, 程树良. 新型钢铅组合耗能器试验研究[J].
工程力学, 2007, 24(3): 126-130.
XIN Yajun, WANG Huanding, CHENG Shuliang. Experimental study on new combined steel-lead damper[J]. Engineering Mechanics, 2007, 24(3): 126-130. DOI: 10.3969/j.issn.1000-4750.2007.03.021 |
| [6] |
辛亚军, 程树良, 王焕定. 一种钢铅组合耗能器的滞回模型和减震效果研究[J].
工程力学, 2010, 27(10): 74-80.
XIN Yajun, CHENG Shuliang, WANG Huanding. Hysteretic model and control effect of a combined steel-lead damper[J]. Engineering Mechanics, 2010, 27(10): 74-80. |
| [7] |
何志明, 周云, 卢德辉, 等. 可更换钢管铅芯阻尼器偏心支撑框架分析[J].
工程抗震与加固改造, 2016, 38(1): 79-88.
HE Zhiming, ZHOU Yun, LU Dehui, et al. Structure analysis of replaceable shear link eccentrically brace with lead-filled steel tube damper[J]. Earthquake Resistant Engineering and Retrofitting, 2016, 38(1): 79-88. DOI: 10.16226/j.issn.1002-8412.2016.01.012 |
| [8] |
卢德辉, 周云, 邓雪松. 钢管铅芯阻尼器性能分析研究[J].
地震工程与工程振动, 2013, 33(6): 215-221.
LU Dehui, ZHOU Yun, DENG Xuesong. Research on performance of lead-filled steel tube damper[J]. Journal of Earthquake Engineering and Engineering Vibration, 2013, 33(6): 215-221. DOI: 10.13197/j.eeev.2013.06.215.ludh.030 |
| [9] | YAN X Y, ZHANG Y S, WANG H D, et al. Research on seismic performance and design method of combined steel lead energy dissipation structure (Ⅰ)[J]. Journal of Harbin Institute of Technology, 2010, 17(3): 376-382. |
| [10] |
颜学渊, 王焕定, 张永山, 等. 钢铅组合耗能器参数优选及减震效果[J].
工程力学, 2009, 26(2): 234-241.
YAN Xueyuan, WANG Huanding, ZHANG Yongshan, et al. Parameter optimizing and cushioning effect of combined steel lead damper[J]. Engineering Mechanics, 2009, 26(2): 234-241. |
| [11] |
颜学渊, 王焕定, 张永山, 等. 新型钢铅组合耗能器性能试验及参数优选[J].
哈尔滨工业大学学报, 2009, 40(12): 20-24.
YAN Xueyuan, WANG Huanding, ZHANG Yongshan, et al. Performance test and parameter optimization of new-style combined steel lead damper[J]. Journal of Harbin Institute of Technology, 2009, 40(12): 20-24. DOI: 10.3321/j.issn:0367-6234.2009.12.004 |
| [12] |
程树良, 刘心洁, 辛亚军, 等. 工字型钢铅组合耗能器减震体系的优化设计研究[J].
工程力学, 2013, 30(9): 166-170, 176.
CHENG Shuliang, LIU Xinjie, XIN Yajun, et al. Study on optimization of structural system with I-section combined steel-lead dampers[J]. Engineering Mechanics, 2013, 30(9): 166-170, 176. |
| [13] |
颜学渊, 祁皑, 陈宏. 椭圆形钢铅耗能器: ZL201420277853. 5[P]. 2014-10-15.
YAN Xueyuan, QI Ai, CHEN Hong. The oval steel-lead damper:ZL201420277853.5[P]. 2014-10-15. |
| [14] |
陈绍蕃.
钢结构设计原理[M]. 北京: 科学出版社, 2005: 151-210.
CHEN Shaofan. Principles of steel structure design[M]. Beijing: Science Press, 2005: 151-210. |
| [15] |
陈宏. 椭圆形钢铅耗能器的试验研究与理论分析[D]. 福州: 福州大学, 2014.
CHEN Hong. Experimental study and theoretical analysis of oval steel-lead damper [D]. Fuzhou: Fuzhou University, 2014. |
 2017, Vol. 49
2017, Vol. 49


