风是由大气相对运动形成的自然现象,大部分建筑物均处于大气边界层中,在靠近地表附近,风受到建筑物的影响而导致湍流度高且风速梯度大,再加上屋盖结构造型的多变,绕流和空气动力学作用相当复杂.当来流到达屋盖的迎风前缘处,边界层将发生流动分离,进而在屋盖表面上方出现各种尺度的旋涡,而随着来流速度大小及风向变化等各种因素的影响,旋涡的位置及其形状大小均处于不断变化当中,随之导致屋面的风压也在发生脉动作用.旋涡诱导的风压脉动将引起屋盖的疲劳破坏,在巨大的风吸力作用下导致屋盖局部区域被掀翻.大跨屋盖的破坏都是始于迎风前缘附近及拐角区域,大跨屋盖抗风设计的安全与否很大程度上取决于这些关键部位的处理.
国内外学者对旋涡作用下的风压脉动特性开展了一系列研究.Mostafa等[1]对大跨平屋盖表面的风压谱进行了研究,指出在屋盖的迎风前缘处测点是以低频为主,随着来流往下游流动,小尺度旋涡的逐渐增多,频谱峰值不断减小且分散于各个频段内.Kasperski等[2]研究了在最不利风向下低矮房屋迎风墙面、迎风屋面、下风屋面及背风墙面的风压谱,给出了其各自的谱形状,但未给出具体的风压谱公式.Chen等[3]研究了双坡屋盖表面测点的风压谱,将其分为三类,第一类谱为标准的宽带谱;第二类谱有两个谱峰,分别出现在低频段和高频段;第三类谱只在中频段出现一个谱峰,之后根据风压谱特征对屋盖表面进行了分区.Nakamura等[4]对拱形悬挑屋盖体育场的风荷载进行了分析,指出模型试验的测点风压功率谱的形状基本一致,与测点位置的关系不大.同时指出在高频段屋盖上表面的风压能量高于下表面,而在低频段屋盖上表面的风压能量低于下表面.Kumar等[5]对不同形状低矮房屋表面的风压谱形状进行研究,结果表明风压谱特性与来流、地貌以及测点所处位置相关.Kiya等[6]对屋盖表面的分离泡结构进行了研究,指出旋涡结构内部不稳定,低频占主导,且分离泡体积在不断放大和缩小.Lee等[7]对台阶表面的风压脉动进行了谱研究,分析发现风压脉动最大值位于旋涡的再附点附近.孙瑛等[8-9],指出屋面风压谱的频谱成分既有大气湍流的影响,还存在特征湍流的成分,且主要以特征湍流影响为主.
本次研究目标是针对三维曲面马鞍体结构,以B类地貌为载体,利用风洞测压试验分析了不同矢跨比和不同迎风面高度下屋盖表面的风压分布特征,重点研究了马鞍屋面风压脉动的频谱特性.通过脉动风压谱揭示了马鞍屋盖迎风前缘的旋涡运动、湍流尺度对于风压分布的影响,建立了谱能量与湍流尺度之间的联系.
1 马鞍屋盖测压方案 1.1 试验概况及模型本次鞍形模型风洞测压试验是在湖南大学HD-2大气边界层风洞的高速试验段中完成.试验段的尺寸分别为7 m长、3 m宽、2.5 m高.模型为刚性模型.模型底面边长为780 mm×780 mm,矢跨比分别为1/6和1/12,两种矢跨比的马鞍模型分别有低点高度为104 mm和208 mm.参考点高度处风速控制在10 m/s,试验中每个测点采集6 600个数据.模拟B类地貌风场时,采用被动模拟,在风洞试验段入口处按规律放置尖塔阵和粗糙元.
考虑到风洞试验段的截面尺寸,将马鞍屋盖模型的几何缩尺比设为1:200,阻塞率约为3%.试验在满足几何相似的基础上,需要同时满足Strouhal相似.由于本试验采用刚性材料制作,因此不考虑刚度受重力的影响,即不考虑Froude相似,相似比设计见表 1.
| 表 1 模型相似比 Table 1 Scaling laws for the wind tunnel test |
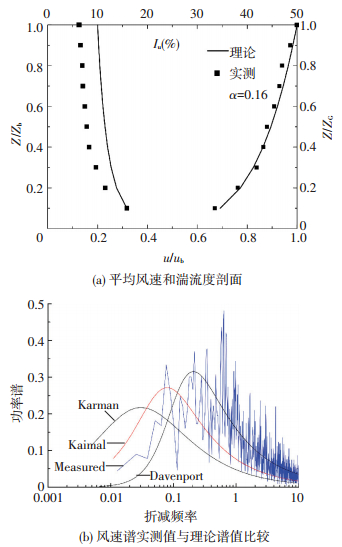
试验室风场模拟出的B类地貌平均风速剖面及湍流度剖面分布见图 1(a),其中ZG为梯度风高度,ub为梯度风高度处的风速,Iu为湍流度.顺风向风速谱实测值与理论谱曲线对比见图 1(b),图中横坐标为折减频率,即Hf/u,其中H为模型特征高度,f为频率,u为模型高度处的平均风速;纵坐标为无量纲化的功率谱值,即fSu(n)/σ2,其中σ2为顺风向风速脉动值的方差.
|
图 1 B类地貌风场模拟 Figure 1 Wind tunnel simulation of terrain B |
由Nyquist Frequency定理可知,对于任意频带受限的信号,用不低于两倍信号的最高频率对其采样,不会丢失信息[10].因此试验中的采样频率应不小于两倍模型的最高频率值,即300 Hz,测压信号的采样频率为331 Hz,满足要求.采样时长一般以保证对应于原型值不小于10 min为宜,根据表 1,该采样时间换算到原型为1 993 s,即33 min,大于规范规定的10 min.综上所述,所测试验结果准确可信.
1.3 测点布置及数据处理由于本文研究的内容基于分离泡作用下屋盖表面的脉动风压效应,因此试验结果的讨论仅限于来流垂直于屋盖的迎风墙面.如图 2所示,马鞍屋盖表面共布置336个测点,规定以压力向下为正,向上吸力为负.

|
图 2 马鞍屋盖模型测点分布 (mm) Figure 2 Measuring point locations and definition of flow directions (mm) |
测点的风压值采用风压系数来表示[11] :
| ${C_{pi}} = \frac{{{P_i}-{P_静}}}{{{P_总}-{P_静}}}.$ | (11) |
式中:Pi为模型第i个测孔测得且修正后的表面风压值;P总和P静分别为参考点处的平均总压和平均静压 (P总=61.817,P静=-1.855).对数据进行处理得到平均风压系数和脉动风压系数.参考点高度取高点与低点之间的平均高度.在得到风压系数时程的基础上对其做脉动功率谱分析,下文中给出的功率谱示意图均是标准化功率谱示意图[12], 图中横纵坐标含义均同图 1(b).
2 试验结果分析 2.1 旋涡作用下的马鞍屋面风压分布图 3~6分别给出了不同矢跨比和不同迎风面高度处马鞍屋盖表面的平均和脉动风压系数等值线图,(a) 中的阴影部分为平均风压系数小于-0.7的区域;(b) 中的阴影部分为脉动风压系数大于0.2的区域.

|
图 3 矢跨比1/12、低点高度104 mm屋面风压分布 Figure 3 Pressure distribution of saddle roof (rise span ratio: 1/12; low point: 104 mm) |
|
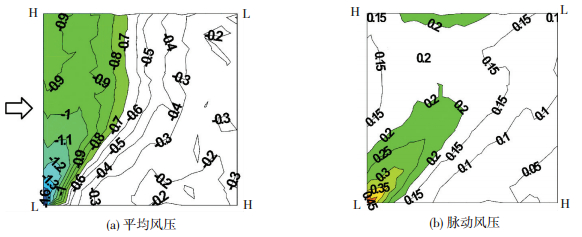
图 4 矢跨比1/12、低点高度208 mm屋面风压分布 Figure 4 Pressure distribution of saddle roof (rise span ratio: 1/12; low point: 208 mm) |
|
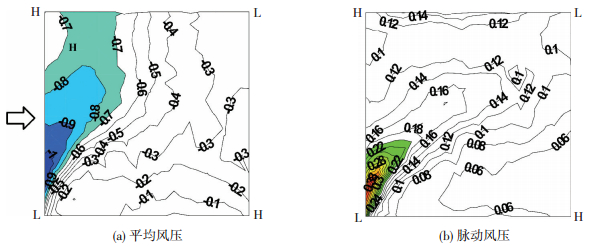
图 5 矢跨比1/6、低点高度104 mm屋面风压分布 Figure 5 Pressure distribution of saddle roof (rise span ratio: 1/6; low point: 104 mm) |
|
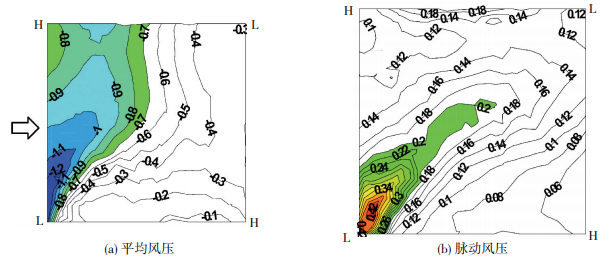
图 6 矢跨比1/6、低点高度208 mm屋面风压分布 Figure 6 Pressure distribution of saddle roof (rise span ratio: 1/6; low point: 208 mm) |
由图 4可知,马鞍形屋盖的风压分布形式上既体现了平屋盖类似的分离泡旋涡作用的特征,又随着屋盖的曲率而变化体现出一定的差异.当来流风向垂直于迎风墙面时,屋盖上的风荷载是以风吸力为主,最大风吸力值出现在迎风屋面低点边缘附近,且平均风压系数的变化梯度较大,而在屋盖迎风高点处风吸力值较小,且变化相对平缓,这说明虽然来流在迎风屋面边缘产生分离,但由于屋盖的迎风面高度不同,因此产生有组织的旋涡活动也不相同.由于从低点到高点存在一定的正向坡度,它能够引导气流向上运动导致屋盖低点处吸力最大.屋盖表面较强的脉动风压则出现在迎风前缘两低点连线前半区域和高点到低点的中部,最大值位于迎风前缘靠近马鞍低点处,屋面其他部位的脉动风压基本相当.
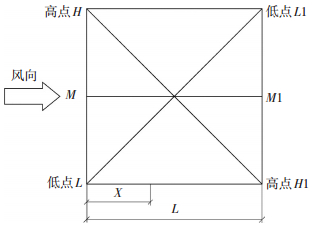
2.2 矢跨比和迎风面高度对风压分布的影响根据马鞍形屋盖特点,取3条关键线上的点进行研究:两高点连成的对角线H-H1;两低点连成的对角线L-L1;迎风前缘中点及对边中点连线M-M1,这些线上点的风压特性能够反映马鞍屋盖的风荷载特性 (图 7).
|
图 7 风向及关键线示意 Figure 7 Wind direction and key line |
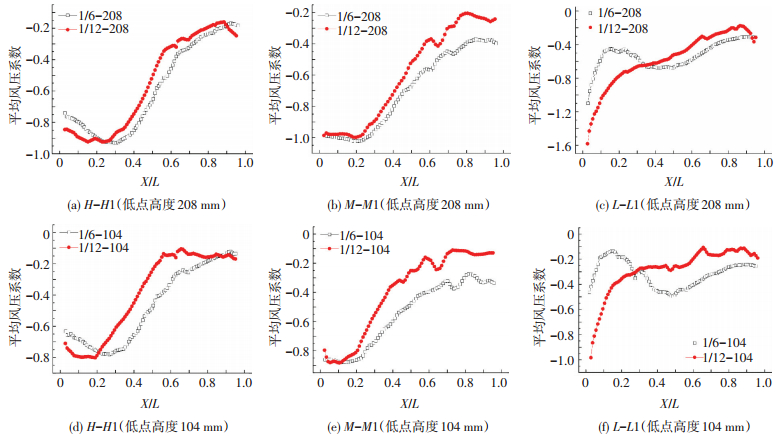
图 8分别给出了马鞍屋面平均风压系数随矢跨比的变化曲线,高点连线下两种矢跨比的平均风压系数比较接近,两者均在屋面的前1/3处达到最大值,随来流的向下游发展,风压系数迅速减小.矢跨比为1/6的其后方区域风吸力相对较大;中点连线时,两种矢跨比下屋面风压系数相当,但随来流往下游发展时,屋盖的后方区域矢跨比较小的其风吸力也较小;对于低点连线而言,两种矢跨比的风荷载在迎风前缘处变化幅度达到最大,矢跨比1/12的风吸力约为1/6的两倍.而在屋盖的背面区,矢跨比1/6的屋面风压系数较小.由以上分析可知,对于高点连线和中点连线,矢跨比对屋面风压的影响主要体现在屋盖后2/3区域,且曲率越大风吸力越大.而在低点连线的迎风前缘,矢跨比1/12的分离效应更为剧烈,导致其风荷载约为矢跨比为1/6的1.5至2倍.从迎风高点至迎风低点,风吸力在不断增大,屋盖后方的风压系数稳定在0.2.迎风前缘低点附近是风荷载最大值点,也是屋盖受到巨大抽吸效应而破坏的关键部位.
|
图 8 不同矢跨比风压对比 Figure 8 Wind pressure comparison with differentrise span ratio |
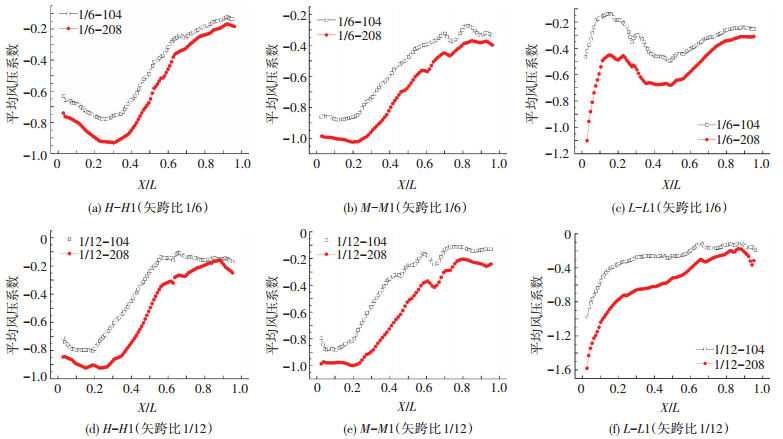
马鞍屋面平均风压系数随迎风墙面高度的变化曲线见图 9.3条关键路线下,迎风面高度越高其风吸力越大,在迎风低点附近其风吸力变化幅度达到最大.因为迎风墙面高度越低,其湍流度越大,旋涡的强度有部分被湍流运动所耗散.相对于矢跨比而言,迎风墙面高度的变化对漩涡脱离作用的影响很大.
|
图 9 不同低点高度风压对比 Figure 9 Wind pressure comparison with different low point height |
风压谱可以反映风压脉动的频域特性,能够建立谱能量与旋涡运动和湍流尺度之间的关系.以顺风向测点列作为研究对象,分为迎风高点列Rank1、中点列Rank14和低点列Rank21(见图 2).马鞍屋盖的迎风高点、中点和低点测点列的脉动风压谱见图 10~12,形状相似的风压谱绘于同一幅图中.

|
图 10 马鞍迎风高点处测点脉动风压谱 Figure 10 Fluctuating wind pressure spectrum of high rank on saddle roof |
|
图 11 马鞍迎风中点处测点脉动风压谱 Figure 11 Fluctuating wind pressure spectrum of middle high rank on saddle roof |
|
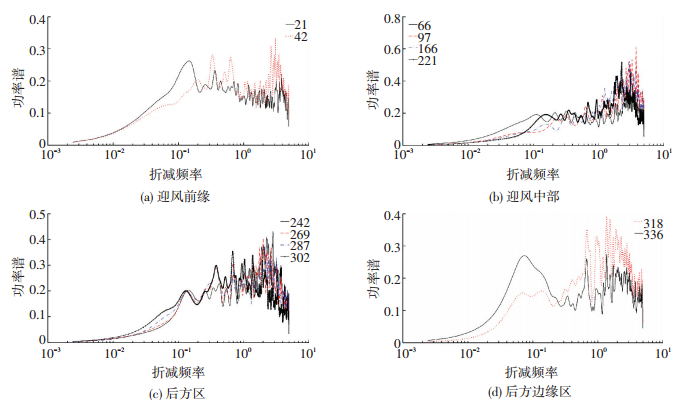
图 12 马鞍迎风低点处测点脉动风压谱 Figure 12 Fluctuating wind pressure spectrum of low high rank on saddle roof |
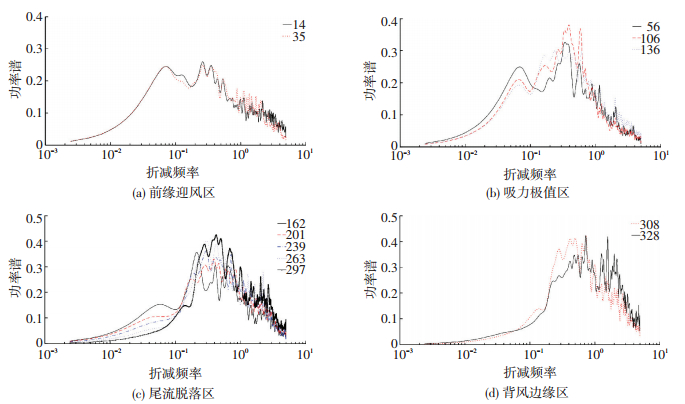
由图 10可知,马鞍屋盖风压谱曲线整体上为较宽的频谱特点.随着测点位置的改变其谱峰值大小、位置和曲线走势均在不断发生变化.在马鞍的迎风前缘高点处脉动风压谱能量中共存在三类频段:低频 (F < 0.1)、中频 (0.1 < F < 1) 和高频 (F>1).迎风高点处谱形状按照测点位置可分为3个区域.
1) 屋面迎风前缘区:剪切层的分离阶段.由图 10(a)可知,脉动风压谱在低频段出现谱峰,此时谱能量最大值达到0.4,其对应的频率主要集中于0.1 Hz处,此后风压谱一直呈衰减状态.在剪切层分离初期,脉动风压中的低频成分占主动,低频主要来源于来流中的大尺度湍流成分和剪切层分离时的逆压卷吸运动.随着测点向屋盖低点移动,风压谱中的低频成分逐渐减少并向中间频段转移,说明来流中的大尺度湍流对脉动风压的影响逐渐减弱,在风压数值上体现为测点1、22、43、67的平均和脉动风压系数均在不断增大 (见表 2).
| 表 2 马鞍迎风前缘高点处Rank1测点风压时程统计值 Table 2 Time series statistics of high point rank 1 on saddle roof |
2) 旋涡吸力极值区:旋涡的形成和发展阶段.由图 10(b)可知,相比于第一阶段,低频能量逐渐减少,风压谱开始向中频发展,谱带变窄,风压谱主峰值有所增大,能量最大值达到0.5.中频段下降斜率相比迎风区急剧增加.风压脉动中的中频成分则是来源于小尺度湍流成分,小尺度湍流是由来流受到马鞍迎风高点的干扰作用而产生于屋盖附面层处.在测点98附近风压谱达到峰值0.46,对应的频率约0.2.此阶段测点的脉动吸力主要来自迎风前缘处剪切层分离运动的影响和旋涡再次卷吸形成的二级涡有关.从风压上看,测点的脉动风压系数也相应增大,相反平均吸力在测点98达到最大值后开始逐渐减小.
3) 后方流动区:旋涡破裂和脱落阶段.从图 10(c)可知,此时测点的脉动风压谱谱峰值在中频段仍然较大,对比迎风前缘区域,其谱峰能量有所减弱且对应的频率为0.5,逐渐向高频靠拢.当来流在屋盖上再附时,分离泡向后方运动受到阻挡而导致内部旋涡破裂,旋涡破裂后可能出现紊乱运动模式,这种模式的不稳定使得风压出现很大脉动.在测点208处脉动风压系数达到最大,但平均风压系数却由于能量的耗散而迅速减小.如图 10(d)所示,随着来流继续往下游发展,风压谱逐渐向高频扩展,高频处的谱能量最大值达到0.35,且高频段开始出现间断式谱峰.此外由于分离泡破裂产生了大量小尺度涡和微尺度涡,它们具有较大粘性应力和剪切变形效应,使气流中的湍流能量快速耗散[11],因此从测点230开始,平均和脉动风压系数开始迅速减小.可以看出,此阶段的旋涡破裂导致谱能量在高频段重新分布且谱能量值较大.
由图 11可知,迎风中点处各测点的脉动风压谱同迎风高点比较类似,谱形状沿顺风向也经历3个阶段:来流在迎风前缘分离阶段,低频脉动为主控,屋面风压主要受到来流远场脉动的直接作用;随着剪切层再附形成分离泡,风压脉动中的中频成分增加,旋涡的近场脉动成为关键因素;当来流到达背风面边缘时,由中频转向高频成分,这是由旋涡的脱落引起.在风压谱经历的3个阶段,迎风中点测点的谱峰值相比于高点测点明显下降,主要原因是由于马鞍在迎风中点处的高度有所降低,马鞍曲率变化较小,减弱了马鞍对来流的干扰作用.由表 3可知,平均风压最大值出现在测点106附近,平均风压最大值点离迎风前缘距离同迎风高点处一致,说明从迎风高点到中点位置分离泡的流动是二维的,风压在横风向表现出强烈且均一的相关特征.
| 表 3 马鞍迎风前缘中点处Rank14测点风压时程统计值 Table 3 Time series statistics of middle high point rank 14 on saddle roof |
如图 12所示,来流在迎风低点区的风压谱形状与迎风高点处差异较大,风压谱曲线总体上呈现宽带特性,各个频率段均有谱峰值,谱峰最大值出现在中高频段.从平均风压数值上看 (表 4),测点21~测点97的平均风压系数变化梯度最大,说明来流在迎风低点屋檐处分离作用更为严重,在剪切层分离时产生的逆压梯度在屋面形成强烈的抽吸作用,同时又受到来流中的湍流成分作用,因此在迎风顶点附近平均和脉动吸力值达到最大,而以来流为主导作用的迎风前缘区范围减小,甚至消失,这也和上风阶段的马鞍曲面相关,因此可以说迎风前缘区域受到特征湍流影响显著.随着来流往下游发展,中频能量开始减少,风压谱开始向高频发展,图 12(b)、(c)中的高频成分说明了存在小尺度湍流促使旋涡的形成.在风压系数上体现为从迎风低点处开始呈一直下降趋势.当来流到达背风面高点时,来流与结构的相互作用显著,高点附近结构对来流造成了干扰,致使脉动风压系数增大.由于干扰作用形成的湍流积分尺度相比于来流的湍流积分尺度小得多,在风压谱上体现为高频脉动 (图 12(d)).
| 表 4 马鞍迎风前缘低点处Rank21测点风压时程统计值 Table 4 Time series statistics of low high point rank 21 on saddle roof |
综上所述,在马鞍形屋盖的迎风前缘区内测点的脉动风压谱曲线与Kaimal谱较为接近.随着来流往下游发展,测点的风压谱出现了明显波动,这与旋涡的脱落特征相关.屋面极值吸力区向中高频移动,谱带变窄且峰值有所增大.这表明了结构对来流的作用逐渐增大,而来流随测点的后移作用减小.特别是对于背风面的测点主要表现为特征湍流的特性.在马鞍屋盖的迎风中点处,风压谱曲线与迎风高点处类似,由于马鞍曲率在迎风中点处基本一致,受屋盖的干扰作用小,其谱峰值较高点也较低.在马鞍屋盖的迎风低点处,由于来流在低点处分离作用更为剧烈,同时又受到来流中的湍流成分作用,因此在迎风顶点附近平均和脉动吸力值达到最大.
3 结论1) 当来流垂直于迎风墙面时,屋盖上的风荷载以风吸力为主,最大风吸力值出现在迎风屋面低点边缘附近,且风压变化梯度较大,而在屋盖迎风高点处风吸力值较小,且变化相对平缓.在迎风前缘低点连线的前半区域风压脉动较强,且最大值出现在迎风前缘低点处,而其他区域脉动风压基本相当.
2) 矢跨比对屋面风压的影响主要体现在屋盖后2/3区域,且曲率越大风吸力越大.但在迎风低点前缘处矢跨比1/12的风荷载约为1/6的1.5~2倍.从迎风高点至迎风低点风吸力在不断增大,迎风低点区域是平均风压和脉动风压最强区,为屋盖破坏的关键部位.
3) 对于大跨马鞍屋盖迎风高点,屋盖迎风前缘区内测点的脉动风压谱曲线与Kaimal谱较为接近.随着来流的往下游发展,测点的风压谱出现了持续抖动,屋面极值吸力区向中高频移动,谱带变窄且峰值有所增大.在迎风中点处,风压谱曲线与迎风高点处类似,由于马鞍曲率在迎风中点处基本一致,受屋盖的干扰作用小,其谱峰值较高点也较低.在迎风低点处,由于来流在低点处分离作用更为剧烈,同时又受到来流中的湍流成分作用,因此在迎风顶点附近平均和脉动吸力值达到最大.
| [1] | MOATAFA N H, HAJJ M R, ZEIGER M D, et al. Space/time characteristics of pressure fluctuations in separation regions[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90: 415-426. DOI: 10.1016/S0167-6105(01)00217-3 |
| [2] | KASPERSKI M, KOSS H, SAHLMEN J. BEATRICE Joint Project: Wind action on low-rise buildings: Part1. Basic information and first results[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1996, 64: 101-125. DOI: 10.1016/S0167-6105(97)00002-0 |
| [3] | CHEN M. Characterization of wind pressure fluctuations on a gable roof house [D]. South Carolina: Clemson University, 2000. |
| [4] | NAKAMURA O, TAMURA Y, MIYASHITA K, et al. A case study of wind pressure and wind induced and wind-induced vibration of a large span open-type roof[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1994, 52: 237-428. DOI: 10.1016/0167-6105(94)90050-7 |
| [5] | KUMAR K S, STATHOPOULOS T. Power spectra of wind pressure on low building roofs[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74/75/76: 665-674. |
| [6] | KIYA M, SASAKI K. Structure of large-scale vortices and unsteady reverse flow in the reattaching zone of a turbulent separation bubble[J]. Journal of Fluid Mechanics, 1985, 154: 463-491. DOI: 10.1017/S0022112085001628 |
| [7] | LEE I, SUNG H J. Characteristics of wall pressure fluctuations in separated and reattaching flows over a backward-facing step: Part Ⅰ. Time-mean statistics and cross-spectral analyses[J]. Experiments in Fluids, 2001, 30: 262-272. DOI: 10.1007/s003480000172 |
| [8] |
孙瑛, 武岳, 林志兴, 等. 大跨度平屋盖表面的特征湍流研究[J].
空气动力学学报, 2007, 25(3): 319-324.
SUN Ying, WU Yue, LIN Zhixing, et al. Characteristics of signature turbulence on long span flat roofs[J]. Acta Aerodynamica Sinica, 2007, 25(3): 319-324. |
| [9] |
孙瑛, 武岳, 林志兴, 等. 大跨度平屋盖表面的风压脉冲特性研究[J].
工程力学, 2007, 24(4): 92-96.
SUN Ying, WU Yue, LIN Zhixing, et al. Characteristics of peak surface pressures on long span flat roofs[J]. Engineering Mechanics, 2007, 24(4): 92-96. |
| [10] |
沈振元, 聂志良, 赵雪荷.
通信系统原理[M]. 西安: 西安电子科技大学出版社, 1993: 280-289.
SHEN Zhenyuan, NIE Zhiliang, ZHAO Xuehe. Principles of communication systems[M]. Xi'an: Xi'an University of Electronic Science and Technology Press, 1993: 280-289. |
| [11] |
孙晓颖, 武岳, 沈世钊. 大跨屋盖风压分布的数值模拟及拟合方法研究[J].
哈尔滨工业大学学报, 2006, 38(4): 53-557.
SUN Xiaoying, WU Yue, SHEN Shizhao. Numerical simulation of wind pressure distribution on long-span roofs and curve fitting method[J]. Journal of Harbin institute of technology, 2006, 38(4): 53-557. |
| [12] |
董欣, 叶继红. 锥形涡及其诱导下的马鞍屋盖表面风荷载[J].
振动与冲击, 2010, 29: 61-70.
DONG Xin, YE Jihong. Conical vortex and its induced wind load on a saddle roof[J]. Journal of vibration and shock, 2010, 29: 61-70. DOI: 10.3969/j.issn.1000-3835.2010.10.013 |
 2017, Vol. 49
2017, Vol. 49


