双曲线冷却塔属于高耸特种结构,在强震作用下容易产生比较严重的破坏[1],有必要对这类重要的工程构筑物进行抗震性能评估以保证其在地震作用下的安全性,而结构的地震易损性是评价其抗震性能优劣的有效方法.
国内外针对钢筋混凝土结构和桥梁结构的地震易损性进行了大量研究:文献[2-3]对钢筋混凝土框架结构的地震易损性进行了研究;文献[4]在其研究中提出了一种用数值模拟建立理论易损性曲线的方法;文献[5]在考虑地震环境和场地影响的基础上对钢筋混凝土房屋的地震易损性进行了研究;文献[6]提出了基于可靠度和性能的整体地震易损性分析方法;文献[7]采用应变作为墩柱损伤指标, 位移作为支座损伤指标,研究了桥梁结构的地震易损性.然而,在对地震易损性的已有研究中,很少有对高耸特种结构尤其是对钢筋混凝土双曲冷却塔的研究.本文在已有研究基础上,重点探讨在不同地震动记录和不同强度地震水平下冷却塔结构各部位发生各级损伤的概率,据此提出结构区域易损性的概念.
区域易损性 (partitioned vulnerability) 是指结构的各个部位在不同强度地震作用下发生各级损伤的概率.本文将冷却塔结构沿高度方向划分为13个区域,通过对比各区域在不同强度地震水平下发生各级损伤的概率,从易损性角度对结构的抗震性能进行评估, 从而得到结构的最薄弱部位,进而可以更加明确地对薄弱部位进行重点加固处理.
采用有限元软件ABAQUS建立了冷却塔结构的分析模型,根据结构所在场地条件从PEER网站选取了15条地震记录;在结构底部施加水平单向、水平双向和三向地震波进行增量动力分析[8](incremental dynamic analysis,IDA),分别选取材料应变和地面峰值加速度 (peak ground acceleration,PGA) 作为结构需求参数和地震动强度参数,基于对数正态分布假设并根据IDA分析所得结构响应,通过回归分析建立结构的地震需求模型,最终得到结构沿高度方向的损伤概率曲线和区域易损性曲线.
1 区域易损性分析理论基础区域易损性和通常的地震易损性采用的基本理论相同:即在给定的地震动强度参数IM下结构的地震损伤Damage超过结构能力Capacity的概率Pf,其数学表达式为
| ${P_{\rm{f}}} = P\left[{{\rm{Damage}} \ge {\rm{Capacity}}\left| {{\rm{IM}}} \right.} \right], $ | (1) |
式中:IM为地震动参数 (此处为地面峰值加速度PGA),Capacity为结构抗震能力,Damage表示损伤指标,Pf表示括号内事件发生的概率.
区域易损性和地震易损性最大的区别在于前者将结构划分为数个小的区域,分别讨论各个小区域的损伤.从而可以精确地找出结构最容易损伤的部位,进而对其采用有效的加固措施.
2 模型建立和地震波选取 2.1 工程概况本文以某发电厂在役钢筋混凝土冷却塔为研究对象,该冷却塔建于20世纪70年代末,其主体结构高度为60 m,下环梁半径22.937 m、喉口半径12 m、塔顶半径13.439 m,塔底围绕塔中心分布有36对截面直径为360 mm的人字型支柱.塔筒的壁厚随冷却塔高度变化,最厚处为450 mm,最薄处仅为120 mm,详细参数见表 1.纵向钢筋与箍筋均采用HRB335.该冷却塔位于辽宁鞍山,抗震设防烈度为7度,设计基本地震水平加速度峰值为0.10g,场地类别为Ⅱ类,设计地震分组为第一组.
| 表 1 冷却塔模型详细构建参数 Table 1 Detailed parameters of the tower modelmm |
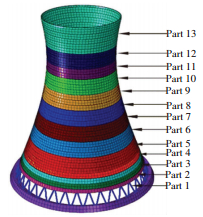
采用ABAQUS软件并基于分层壳模型建立了整个冷却塔结构的三维模型,见图 1.
|
图 1 基于ABAQUS的三维有限元模型 Figure 1 3D model based on ABAQUS |
其中上部塔筒选用壳单元S4R进行模拟,底部人字型支柱采用梁单元B31进行模拟.有限元模型的自振频率与实测值的对比见表 2,模拟值与实测值吻合度良好.
| 表 2 有限元模拟和实测值的频率值对比 Table 2 Frequency comparison of finite element simulation and measured values |
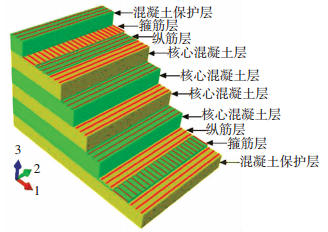
用来模拟塔筒的壳单元沿壳厚度方向分为10层,分别为内外侧混凝土保护层、内外侧箍筋层和纵筋层以及4层核心混凝土层,具体分层壳模型见图 2.
|
图 2 基于ABAQUS的分层壳模型 Figure 2 Layered shell model based on ABAQUS |
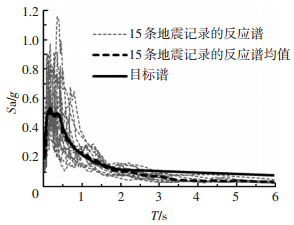
地震的不确定性是影响时程分析结果的重要因素之一,选取的地震动记录越多,地震动的不确定性就越能得到充分考虑.鉴于中国地震记录较少,本文根据结构所在场地条件,以抗震设计规范规定的地震动设计反应谱为目标谱,从美国太平洋地震中心数据库中选取了15条地震动记录 (见表 3),所选取的地震波对应的反应谱与规范谱的拟合见图 3(纵轴表示谱加速度Sa/g, 横轴表示周期T/s).由图 3可见,所选的15条地震波的平均反应谱和目标反应谱在周期T=0~2.8 s范围内吻合较好, 而该冷却塔前四阶自振周期均落在该范围内,说明所选地震波较为合适.
| 表 3 用于增量动力分析的地震波 Table 3 List of earthquake ground motions used for the incremental dynamic analysis |
|
图 3 所选地震波反应谱 Figure 3 Response spectrum of selected seismic wave |
概率抗震能力分析的目的是建立概率抗震能力模型,即在给定某地震需求下,结构或构件发生某一损伤等级的条件概率.要实现这一目的,首先必须选择合适的损伤指标并划分损伤等级,还要确定各极限状态之间的临界值.
3.1 损伤指标的确定和损伤等级划分基于性能的抗震设计方法强调在不同的性能目标下结构有不同的破坏状态.因此,选择合适的损伤指标非常重要[9].已有研究表明,选取应变或从应变状态计算得到的截面曲率作为高耸结构的损伤指标更合理[10].国内外学者对结构损伤指标的研究中很多都采用变形作为结构的损伤指标[11-13].鉴于此,本文选用材料应变作为损伤指标.
强度指标IM就是在IDA分析中一种用来表征地面运动强度大小的参数指标.文献[14]分别选取了地面峰值加速度PGA、地面峰值速度PGV (peak ground velocity) 和地面峰值位移PGD (peak ground displacement) 等作为强度指标对其适用性进行分析;文献[15]对不同的IM进行评估,认为PGA是IM的最优选择.本文选取PGA作为地震动强度指标IM.
地震易损性分析中,通常将结构在地震作用下的破坏程度划分为若干等级,并确定相应的极限状态 (limite state, LS).根据《建 (构) 筑物地震破坏等级划分》[16]中的相关规定,将冷却塔的损伤状态划分为5个等级,确定4个极限状态LS-1、LS-2、LS-3和LS-4.
3.2 极限状态的确定1) 第一极限状态LS-1(对应于轻微损伤).根据文献[17],定义混凝土第一极限状态压应变限值εc1=0.86εp,而第一极限状态的钢筋拉应变限值为εs1=εy;εp为混凝土峰值应变,εp通常取0.002;εy为钢筋的屈服应变,εy=0.001 5.
2) 第二极限值状态LS-2(对应于中等损伤).借鉴文献[18]以及中国、美国和欧洲混凝土设计规范[19-21],定义第二极限值状态的混凝土压应变限值为εc2=0.003 5;钢筋拉应变限值为εs2=0.006.
3) 第三极限状态LS-3(对应于严重损伤).依据文献[22]对中空圆形柱的试验和文献[23]对混凝土空心桥墩试验研究,定义第三极限状态的混凝土压应变限值为εc3=0.005;钢筋拉应变限值取为εs3=0.03.
4) 第四极限状态LS-4(对应于完全损伤).根据美国混凝土设计规范[20]、文献[22-24],定义εc4=0.008作为第四极限状态的混凝土压应变限值,钢筋拉应变限值取εs4 =0.05,当结构达到此极限状态时,认为结构已经倒塌.
钢筋混凝土冷却塔结构的损伤指标限值见表 4.
| 表 4 损伤指标限值 Table 4 Definition of damage limit states |
利用IDA分析结果进行最小二乘法的二次多项式回归,得到回归均值λ和标准差σ,具体计算方法见式 (2)、(3),然后利用式 (4) 计算出各级损伤的概率,进而得到易损性曲线.
| $\lambda = a{\left[{\ln \left( {{\rm{PGA}}} \right)} \right]^2} + b\ln \left( {{\rm{PGA}}} \right) + c, $ | (2) |
| $\sigma = \sqrt {\frac{{\sum\nolimits_{i = 1}^N {{{\left\{ {\ln {d_i}- a{{\left[{\ln \left( {{\rm{PGA}}} \right)} \right]}^2} -b\ln \left( {{\rm{PGA}}} \right) -c} \right\}}^2}} }}{{N -2}}}, $ | (3) |
| ${P_{\rm{f}}} = P\left[{\frac{{{S_{\rm{d}}}}}{{{S_{\rm{c}}}}} \ge 1} \right] = 1 - \mathit{\Phi }\left[{\frac{{\ln \left( 1 \right)-\lambda }}{\sigma }} \right] = \mathit{\Phi }\left[{\frac{\lambda }{\sigma }} \right].$ | (4) |
式中:a、b、c是可以通过回归分析得到的系数,N表示所有离散点的个数,Sd表示结构需求,Sc表示结构能力.
4 冷却塔结构的区域易损性分析对选取的15条地震波均按PGA进行步长为0.1g的等步调幅,对调幅后的每一条地震波分别以单向 (水平1方向-1D)、水平双向 (1*水平1方向+0.85*水平2方向-2D)、三向 (1*水平1方向+0.85*水平2方向+0.65*竖向-3D)3种地震波输入方式施加到结构底部,对调幅后得到的540条地震波分别进行弹塑性动力时程分析,将结果进行统计分析后得到结构的损伤概率曲线和区域易损性曲线.
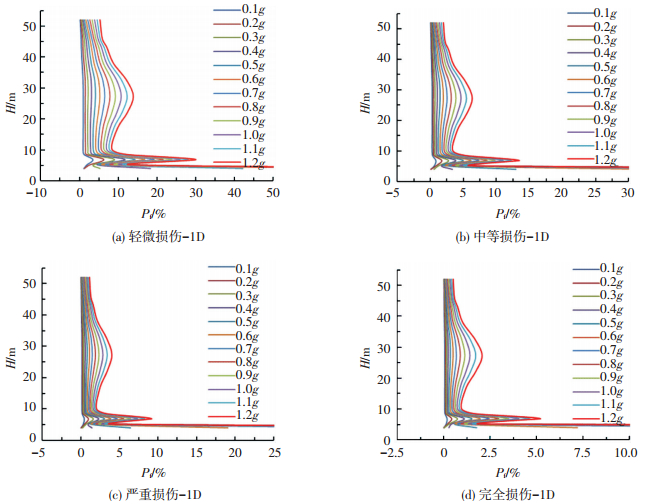
4.1 沿结构高度方向的损伤概率曲线将结构各区域所对应的高度与该区域在各强度地震作用下对应的损伤概率绘制在同一坐标系中,得到结构不同高度处的损伤概率曲线,见图 4、5、6(纵轴表示高度H/m,横轴表示损伤概率Pf/%),其中每张图中所含的12条曲线自左向右分别对应0.1g~1.2g.
|
图 4 单向地震作用下沿高度方向的损伤概率曲线 Figure 4 Damage probability curve along the height direction under unidirectional seismic |
|
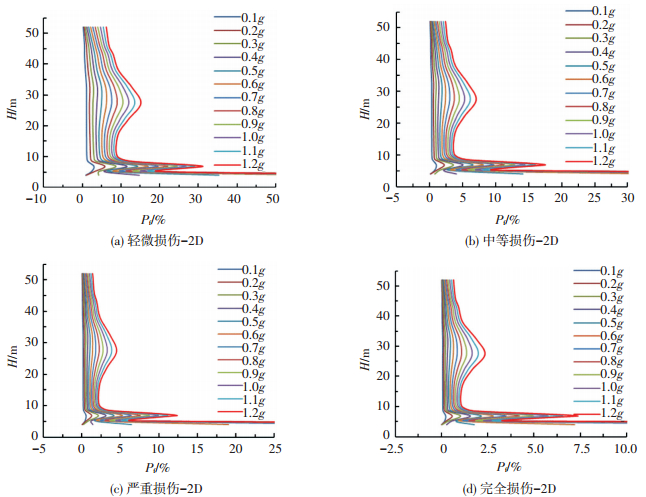
图 5 水平双向地震作用下沿高度方向的损伤概率曲线 Figure 5 Damage probability curve along the height direction under bidirectional horizontal seismic |
|
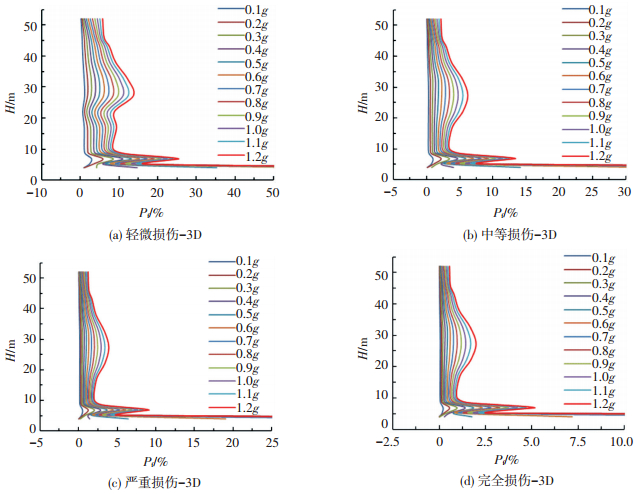
图 6 三向地震作用下沿高度方向的损伤概率曲线 Figure 6 Damage probability curve along the height direction under three-dimensional seismic |
由图 4~6可看出:在单向地震、水平双向地震和三向地震作用下,在高度方向上各区域损伤概率的变化趋势大致相同.人字柱部分 (0~4.0 m) 发生损伤的概率最大,是结构最薄弱的部位;下环梁上部的一定范围内 (5.2~8.6 m) 也是损伤比较容易发生的部位,但相对人字柱部分来说损伤概率要小很多;喉部以下部分 (22.1~38.0 m) 是冷却塔结构容易发生损伤的第三大部位,但是其危险性已经大大减弱;而其余两大范围 (8.6~22.1 m, 38.0~60.0 m) 的损伤概率均在4%以内,是结构相对安全的部位.另外还可看出,在0~4.0 m范围内,PGA从0.3g增加到1.0g的过程中曲线的增幅比较大,说明此部位对小震和大震都很敏感.
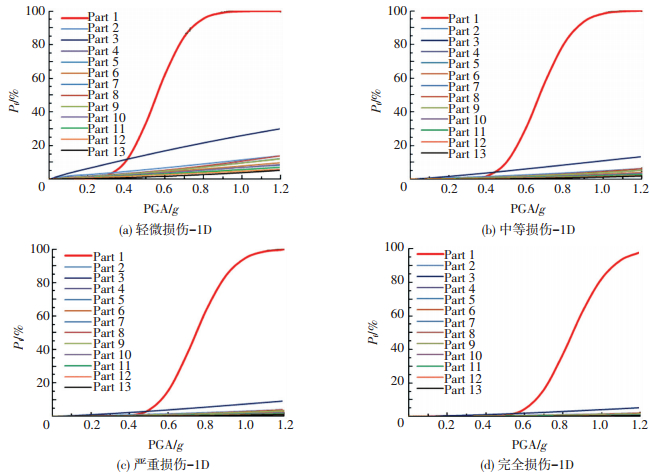
4.2 区域易损性曲线沿高度将冷却塔结构划分为13个区域,其中下部反应较大的区域划分较密,具体如下:人字柱-Part1为0~4 m;Part2为4~5.2 m;Part3为5.2~6.9 m;Part4为6.9~8.6 m;Part5为8.6~10.2 m;Part6为10.2~17.0 m;Part7为17.0~22.1 m;Part8为22.1~27.3 m;Part9为27.3~32.5 m;Part10为32.5~38.0 m;Part11为38.0~44.0 m;Part12为44.0~52.0 m;Part13为52.0~60.0 m.由式 (2)~(4) 可得出结构的每一个区域在PGA从0.1g增加到1.2g的损伤概率,每个区域对应一条损伤概率随PGA变化的曲线,具体见图 7~9, 每张图包含的13条曲线自上向下对应的高度逐渐增大.
|
图 7 单向地震作用下的区域易损性曲线 Figure 7 Partitioned vulnerability curve under unidirectional seismic |
|
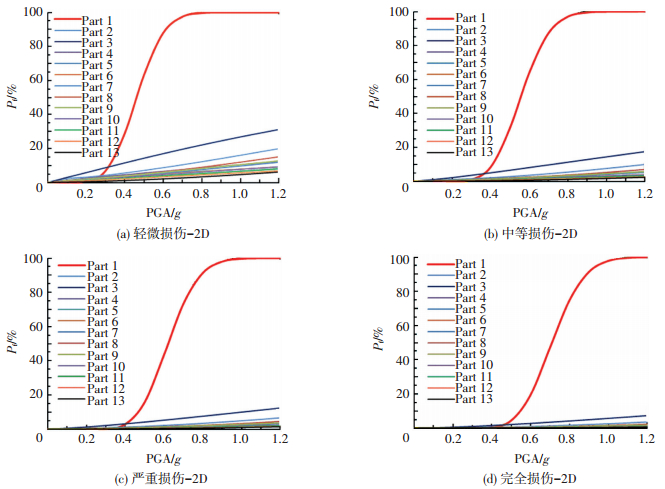
图 8 水平双向地震作用下的区域易损性曲线 Figure 8 Partitioned vulnerability curve under bidirectional horizontal seismic |

|
图 9 三向地震作用下的区域易损性曲线 Figure 9 Partitioned vulnerability curve under three-dimensional seismic |
从图 7~9可看出:当PGA < 0.3g时,整个结构各部位的损伤概率都很小,基本上处于弹性工作状态,此时Part3和Part4 (5.2~8.6 m) 是损伤概率最大的部位;随着PGA进一步增大,Part1(0~4 m) 的损伤概率明显增大,且明显大于其他部位,因此在预测结构易损性时,0~0.3g内选用Part3和Part4 (5.2~8.6 m) 的损伤概率、0.3~1.2g内选用Part1 (0~4.0 m) 的损伤概率将会与实际更接近.另外,对于人字柱部分,在0.4~0.8g范围内,水平双向地震作用下的损伤概率比单向地震作用下有较明显的提高,而考虑竖向地震作用后,其损伤概率变化不大;其余部分在单向、水平双向和三向地震作用下的损伤概率相差不大.单向地震作用下,人字柱部分在0.6g时才出现倒塌,而在水平双向和三向地震作用下,倒塌出现提前至0.5g;其余部分的倒塌概率基本为0.
PGA在0~0.3g范围内,各部位的损伤概率差别不大;PGA超过0.3g以后,0~4 m范围内 (人字柱) 的损伤将变得突出,同样说明了该部位是整个结构的最危险部位.由以上分析可知,无论是在单向地震还是多维地震作用下,冷却塔底部的人字柱都是结构的最薄弱部位,在设计和应用中可根据需要进行重点加强和加固处理,可以采用如下几种处理方案:1) 改变人字柱的材料属性,提高截面刚度;2) 在人字柱反应最大的部位安装阻尼器,通过耗能减轻人字柱的反应和损伤;3) 采用增大截面法对人字柱进行加固.
5 结论1) 通过将结构划分区域并讨论各个区域的易损性和抗震性能,可从概率角度定量地找出结构的最薄弱部位,从而为结构加强和加固提供理论依据.
2) 由结构沿高度方向的损伤概率曲线和区域易损性曲线可知,人字柱是结构的最薄弱部位,其损伤概率明显大于结构的其他部位.
3) 在评价该结构在地震作用下的易损性时,宜采用分级评价的方法,即PGA < 0.3g时选用下环梁上部区域 (5.2~8.6 m) 的易损概率来代表整个结构;而PGA>0.3g时选用人字柱 (0~4 m) 的易损性来表征整个结构.
4) 沿高度方向的损伤概率曲线和区域易损性曲线都说明水平双向地震作用下结构的反应比单向地震时明显变大,而竖向地震对结构反应的影响不大.对于冷却塔结构来说,在进行抗震分析时可只考虑水平方向的地震作用.
| [1] |
陈卫兵. 双曲线冷却塔结构动力特性研究[D]. 武汉: 武汉大学, 2005.
CHEN Weibing.Dynamic study of hyperbolic cooling towers[D].Wuhan: Wuhan University, 2005. |
| [2] |
吕大刚, 于晓辉, 陈志恒. 钢筋混凝土框架结构侧向倒塌地震易损性分析[J].
哈尔滨工业大学学报, 2011, 43(6): 1-5.
LU Dagang, YU Xiaohui, CHEN Zhiheng. Lateral seismic collapse fragility analysis of RC frame structures[J]. Journal of Harbin Institute of Technology, 2011, 43(6): 1-5. DOI: 10.11918/j.issn.0367-6234.2011.06.001 |
| [3] | SCHOTANUS M I J, FRANCHIN P, LUPOI A, et al. Seismic fragility analysis of 3D structures[J]. Structural Safety, 2004, 26(4): 421-441. DOI: 10.1016/j.strusafe.2004.03.001 |
| [4] | KARIM K R, YAMAZAKI F. Effect of earthquake ground motions on fragility curves of highway bridge piers based on numerical simulation[J]. Earthquake engineering & structural dynamics, 2001, 30(12): 1839-1856. DOI: 10.1002/eqe.97 |
| [5] |
温增平, 高孟潭, 赵凤新, 等. 统一考虑地震环境和局部场地影响的建筑物易损性研究[J].
地震学报, 2006, 28(3): 277-283.
WEN Zengping, GAO Mengtan, ZHAO Fengxin, et al. Seismic vulnerability estimation of the building considering seismic environment and local site condition[J]. Acta Seismologica Sinica, 2006, 28(3): 277-283. |
| [6] |
常泽民. 钢筋混凝土结构非线性抗震可靠度及地震易损性分析[D]. 哈尔滨: 哈尔滨工业大学, 2006.
CHANG Zemin.Nonlinear seismic reliability and fragility analysis of RC structures[D].Harbin: Harbin Institute of Technology, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10213-2007033944.htm |
| [7] |
谷音, 黄怡君, 卓卫东. 高墩大跨连续刚构桥梁地震易损性分析[J].
地震工程与工程振动, 2011, 31(2): 91-97.
Y in, HUANG Yijun, ZHUO Weidong. Study on seismic vulnerability of long-span continuous rigid frame bridge with high piers[J]. Earthquake Engineering and Engineering Vibration, 2011, 31(2): 91-97. DOI: 10.13197/j.eeev.2011.02.010 |
| [8] | VAMVATSIKOS D, CORNELL C A. Incremental dynamic analysis[J]. Earthquake Engineering & Structural Dynamics, 2002, 31(3): 491-514. DOI: 10.1002/eqe.141 |
| [9] |
吴文朋, 李立峰, 王连华, 等. 基于IDA的高墩大跨桥梁地震易损性分析[J].
地震工程与工程振动, 2012, 32(3): 117-123.
Wenpeng, LI Lifeng, WANG Lianhua, et al. Evaluation of seismic vulnerability of high-pier long-span bridge using incremental dynamic analysis[J]. Earthquake Engineering and Engineering Vibration, 2012, 32(3): 117-123. DOI: 10.13197/j.eeev.2012.03.009 |
| [10] |
焦驰宇. 基于性能的大跨斜拉桥地震易损性分析[D]. 上海: 同济大学, 2008.
JIAO Chiyu.Seismic vulnerability analysis of big span cable-stayed bridge based on performance[D].Shanghai: Tongji University, 2008. http://d.wanfangdata.com.cn/Thesis_Y1450091.aspx |
| [11] | ZHANG X, WONG K K F, WANG Y. Performance assessment of moment resisting frames during earthquakes based on the force analogy method[J]. Engineering Structures, 2007, 29(10): 2792-2802. DOI: 10.1016/j.engstruct.2007.01.024 |
| [12] | LEHMAN D, MOEHLE J, MAHIN S, et al. Experimental evaluation of the seismic performance of reinforced concrete bridge columns[J]. Journal of Structural Engineering, 2004, 130(6): 869-879. DOI: 10.1061/(ASCE)0733-9445(2004)130:6(869) |
| [13] | KOWALSKY M J. A displacement-based approach for the seismic design of continuous concrete bridges[J]. Earthquake engineering & structural dynamics, 2002, 31(3): 719-747. DOI: 10.1002/eqe.150 |
| [14] |
周光鑫. 超高层建筑地震动强度指标适用性研究[D]. 重庆: 重庆大学, 2015.
ZHOU Guangxin.Study on applicability of ground motion intensity measures for seismic design of super high-rise buildings[D].Chongqing: Chongqing University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10611-1015969859.htm |
| [15] | PADGETT J E, NIELSON B G, DESROCHES R. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios[J]. Earthquake Engineering and Structural Dynamics, 2008, 37(5): 711-726. DOI: 10.1002/eqe.782 |
| [16] |
建 (构) 筑物地震破坏等级划分: GB/T 24335-2009 [S]. 北京: 中国标准出版社, 2009.
Classification of earthquake damage to buildings and special structures: GB/T 24335-2009 [S].Beijing: China Standard Press, 2009. |
| [17] |
过镇海, 时旭东.
钢筋混凝土原理和分析[M]. 北京: 清华大学出版社, 2003.
GUO Zhenhai, SHI Xudong. Reinforced concrete theory and analysis[M]. Beijing: Tsinghua University Press, 2003. |
| [18] | PRIESTLEY M J N. Displacement-based seismic assessment of reinforced concrete buildings[J]. Journal of Earthquake Engineering, 1997, 1(1): 157-192. DOI: 10.1080/13632469708962365 |
| [19] |
混凝土结构设计规范: GB 50010-2010 [S]. 北京: 中国建筑工业出版社, 2010.
Code for design of concrete structures: GB 50010-2010[S].Beijing: China Architecture & Building Press, 2010. |
| [20] | Building code requirements for structural concrete and commentary: ACI 318[S].Michigan: American Concrete Institute, 2008. |
| [21] | European Prestandard.European code2: Design of concrete structures: ENV1992[S].Brussels: European Committee for Standardization, 1992. |
| [22] | HOSHIKUMA J, PRIESTLEY M J N.Flexural behavior of circular hollow columns with a single layer of reinforcement under seismic loading[R].San Diego: University of California, 2000. |
| [23] |
韩强, 周雨龙, 杜修力. 钢筋混凝土矩形空心桥墩抗震性能[J].
工程力学, 2015, 32(3): 28-40.
Qiang, ZHOU Yulong, DU Xiuli. Seismic performance of reinforced concrete rectangular hollow bridge columns[J]. Engineering Mechanics, 2015, 32(3): 28-40. DOI: 10.6052/j.issn.1000-4750.2013.11.1020 |
| [24] |
谷音, 钟华, 卓卫东. 基于性能的矮塔斜拉桥结构地震易损性分析[J].
土木工程学报, 2012, 45(S1): 218-222.
Y in, ZHONG Hua, ZHUO Weidong. Lower-tower cable-stayed bridge seismic vulnerability analysis[J]. China Civil Engineering Journal, 2012, 45(S1): 218-222. DOI: 10.15951/j.tmgcxb.2012.s1.01 |
 2017, Vol. 49
2017, Vol. 49


