2. 同济大学 上海防灾救灾研究所,上海 200092
2. Shanghai Institute of Disaster Prevention and Relief, Tongji University, Shanghai 200092, China
衰减关系是地震动预测的一种重要方法.1961年,Karnal[1]最早提出了点源衰减模型,用震中 (源) 距来表示距离参数,模型对大震近场地震动的拟合偏差较大.大震近场是震害最为严重的区域[2],该区域地震动拟合的准确性对地震动的预测工作至关重要.1977年,Kiureghian等[3]考虑大震引发的断层破裂对地震动的影响,提出了断层破裂衰减模型,该模型对大震地震动的拟合精度有了大幅度提高.随后,断层破裂模型得到大规模地应用,并不断发展.近些年,由太平洋地震研究中心主导的NGA[4](新一代地震动衰减模型) 项目的衰减关系就是以该模型为基础,还考虑了包括上盘效应、断层类型、场地条件等诸多因素的影响.
地震动衰减关系的研究已经从最初只考虑震级和距离到多种因素的综合研究;研究方法也从简单的回归统计到基于地震学和随机振动等多种理论的模拟和拟合的结合.当然,回归精度也逐步提高,但同时却遇到另一问题:模型拟合的对象是已发地震,参数都为已知量;地震动预测,对象为未发生的地震,以NGA为代表的模型中多数参数都无法准确预知,如断层距、上盘效应、断层类型、断层破裂方向等,只能建立很多假设,而这又增加了模型的不确定性.
中国是一个地震频发的国家,由于地震台网建设缓慢,地震动记录,特别是强震记录较为贫乏.目前,中国广泛应用的衰减关系是建立在烈度基础上的椭圆模型[5].汶川地震后,罗奇峰等[6-8]考虑上盘效应及断层破裂方式对地震动的影响,分别提出4区域、6区域和“映射圆”的汶川地震峰值加速度的椭圆衰减关系模型.回归结果比较理想,但距离参数的转换过程极其繁琐,模型很难得到推广应用.
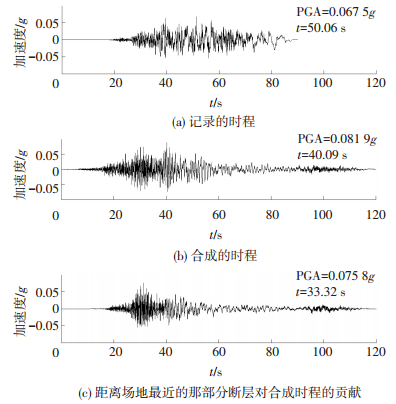
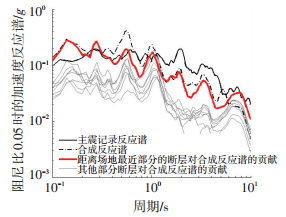
1 多圆组合模型的提出地震学理论中有用余震或前震时程来合成主震时程的方法——经验格林函数法[9-11].用罗奇峰[10]的方法合成1999年集集地震一近场台站 (编号CNY033,位于断层的南端,断层距为40 km) 主震东西向的加速度时程 (图 1).主断层沿走向被等分为多部分,从图 1可以看到,合成加速度峰值比较接近记录到的加速度峰值;距离场地最近的部分断层对合成加速度贡献的峰值又接近合成加速度峰值.图 2为记录的加速度反应谱与合成加速度反应谱的比较,从图中同样可以看到,合成加速度反应谱与记录加速度反应谱差别也不大;相比于其他部分,距离场地最近的部分断层对各个周期合成反应谱的贡献占主导地位.以上合成结果说明:经验格林函数法对近场地震动的合成较为理想,离场地较近的那部分断层对合成地震动的贡献最大.因此,可以得到一个与文献[10]相同的结论:大震近场地震动主要与离场地较近的那部分断层有关.
|
图 1 合成加速度时程与记录时程的比较 Figure 1 Comparing synthetizing acceleration time-series with recording ones |
|
图 2 反应谱曲线比较 Figure 2 Comparison of response spectrum |
基于以上分析,提出一种新的地震动衰减关系模型——多圆组合模型.基本设想如下:
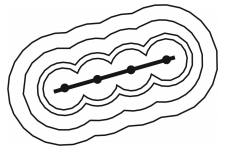
地震引发的主断层破裂被分成多个子断层的组合,假设每个子断层都有一个中心,它为子断层的子源震中 (对于震中所在的子断层,震中即为子源震中),子断层对场地地震动的影响用点源模型来模拟.认为临近场地的子断层对该场地地震动的影响最大,而其他子断层对场地地震动的影响与其相比可以忽略.这样模拟的地震动等值线近似多个圆型的组合 (图 3).场地到该子源震中的距离,定义为子源震中距.
|
图 3 多圆组合模型原理 Figure 3 The principle of multi-circle model |
刘平等[12]利用本模型对汶川地震的峰值加速度进行了初步分析,结果表明模型对汶川地震峰值加速度的拟合基本合理.本文将结合NGA的地震动数据库拟合多圆组合衰减关系,进一步验证模型的可靠性.
2 模型的建立NGA的强震数据库[13]包括173次地震中1 456个台站上记录的3 551组地震动分量数据.全部地震的矩震级在5~8.5之间,台站的断层距在200 km之内.每个记录有131个参数分别描述地震震源、传播路径、局部场地条件和地震动等特征,信息量极大.
2.1 子断层的划分及子源震中距对于小震,由于地震引发的断层破裂较短,可认为只有一个子断层;随着震级增大,断层长度增长,可划分为多个子断层.AS08[14]模型认为当矩震级小于6级时,断层距、震中距等距离参数差别不大.本文将小震界定为矩震级小于6.Mark等[15]的结果计算出6级地震的断层破裂长度约为16 km.所以,当发震断层破裂小于16 km时,认为只有一个子断层;大于16 km时,就考虑用多个子断层来划分发震断层.子源震中距的具体求法分3种情况.
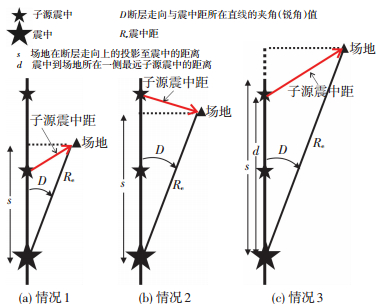
1) 场地在断层走向上的投影位于两子源震中之间,s除以16的余数≤二分之一子断层长度 (图 4(a)):
| ${R_{\rm{m}}} = \sqrt {{\rm{rem}}{{\left( {s, 16} \right)}^2} + {{\left[{{R_{\rm{e}}} \cdot \sin \left( D \right)} \right]}^2}} .$ | (1) |
2) 场地在断层走向上的投影位于两子源震中之间,s除以16的余数 > 二分之一子断层长度 (图 4(b)):
| ${R_{\rm{m}}} = \sqrt {{{\left[{16-{\rm{rem}}\left( {s, 16} \right)} \right]}^2} + {{\left[{{R_{\rm{e}}} \cdot \sin \left( D \right)} \right]}^2}} .$ | (2) |
3) 场地在断层走向上的投影在断层最外侧的子源震中以外 (图 4(c)):
| ${R_{\rm{m}}} = \sqrt {{{\left[{{R_{\rm{e}}} \cdot \cos \left( D \right)-d} \right]}^2} + {{\left[{{R_{\rm{e}}} \cdot \sin \left( D \right)} \right]}^2}} .$ | (3) |
式中:s为场地在断层走向上的投影到震中的距离 (当投影点在断层以外时,为震中到断层一侧端点的距离),Re为震中距,D为断层走向与震中距所在直线的夹角 (锐角) 值,d为震中到最外侧的子源震中的距离,Rm为子源震中距,rem为求余函数.
|
图 4 子源震中距求解原理 Figure 4 The principle of geting sub-source epicentral distance |
考虑到上盘效应和发震断层性质无法预测,而场地条件为已知量,模型的形式为
| $\ln Y = a + bM + c\ln \left( {{R_{\rm{m}}} + H} \right) + {f_{\rm{S}}}\left( {{V_{{\rm{S30}}}}} \right).$ | (4) |
式中:Y为地震动参数,M为矩震级,H为近场饱和因子,fS为场地放大作用 (通过剪切波速VS30反映),VS30为地面以下30 m范围内剪切波速的平均值,其他参数由回归过程确定.
首先,由实际的地震动反算出基岩地震动[16]:
| $\ln {Y_{\rm{R}}} = \ln Y-{f_{\rm{S}}}\left( {{V_{{\rm{S30}}}}} \right), $ | (5) |
回归关系式变为
| $\ln {Y_{\rm{R}}} = a + bM + c\ln \left( {{R_{\rm{m}}} + H} \right), $ | (6) |
式中YR为基岩地震动.
衰减关系的回归采用加权两步法[17],考虑震级的饱和现象,引入转折震级.在第二步回归中,小于转折震级时,第一步回归的震级项是震级的二次函数.回归关系式作如下改变:
| $\ln {Y_{\rm{R}}} = \left\{ \begin{array}{r} a + {b_1}\left( {M-7} \right) + e{\left( {M-7} \right)^2} + c\ln \left( {{R_{\rm{m}}} + H} \right), \\ M < 7;\\ a + {B_2}\left( {M-7} \right) + c\ln \left( {{R_{\rm{m}}} + H} \right), \;\;\;\;\;\;\;\;M \ge 7. \end{array} \right.$ | (7) |
模型选取自由场地上的主震记录,最终57个地震的1 532组记录用于衰减关系的拟合.回归结果见表 1.
| 表 1 回归结果 Table 1 Regression results |
图 5为第一步的观察值与预测值 (拟合结果) 的比值在以子源震中距为横坐标的坐标系下的分布.图 5(a)为矩震级≤7的地震;图 5(b)为矩震级 < 7的地震 (集集地震的记录较多,单独列出).观察值和预测值的比值多数都在0.5~2的范围内波动;表 1第一步的回归标准差在0.53~0.68之间.从结果来看,第一步对地震动的拟合比较理想.
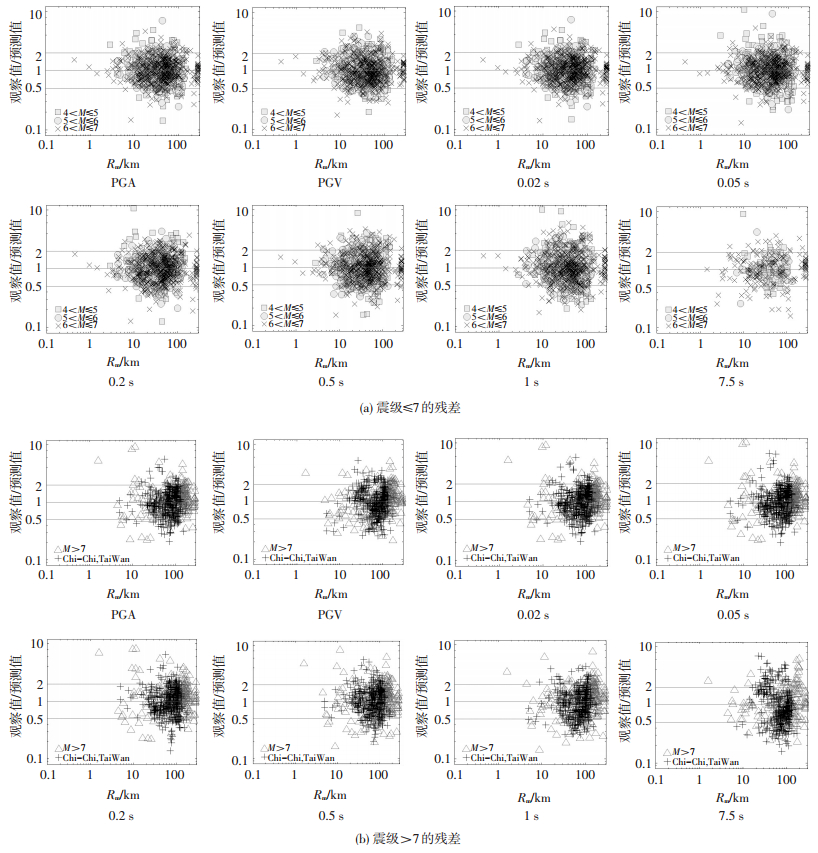
|
图 5 第一步的残差分析 Figure 5 Stage 1 residuals |
图 6为第二步的拟合曲线 (图中实线) 及震级项Ai(第一步拟合确定,i表示第i个地震) 在震级为横坐标的坐标系中的分布.从拟合曲线及震级项的分布来看,转折震级前后曲线及震级项的分布并不相同,第二步采用分段回归的方法比较合理.从表 1的回归标准差来看,第二步对震级项的拟合也比较理想.
3.2 断层类型的影响本文模型中虽未考虑断层类型对地震动的影响,但该问题仍然值得探讨.为研究该问题,对第二步回归关系式作如下调整:
| ${A_i} = \left\{ \begin{array}{r} {a_1}N + {a_2}R + {a_3}S + {b_1}\left( {M-7} \right) + e{\left( {M-7} \right)^2}, \\ M < 7;\\ {a_1}N + {a_2}R + {a_3}S + {B_2}\left( {M-7} \right), \;\;\;\;\;\;\;M \ge 7. \end{array} \right.$ | (8) |
式中:Ai为震级项,M为矩震级,N、R、S均为虚设函数 (对应正断层、逆断层及走滑断层分别取1;其他情况取0),a1、a2、a3、b1、B2为回归系数.
将回归出的曲线及震级项按断层类型绘于以震级为横坐标的坐标系中 (图 6).震级项的分布对于不同断层类型有极强的分选性.相同震级下,正断层值较小,逆断层值较大,走滑断层值介于两者之间, 回归曲线也表现出同样的特征.与不考虑断层类型的拟合曲线 (实线) 比较,这些曲线有以下几个特点:矩震级≤7曲线段的曲率稍有减小;矩震级 > 7直线段的斜率同样稍有减小.以上结果表明, 断层类型对地震动有一定影响.
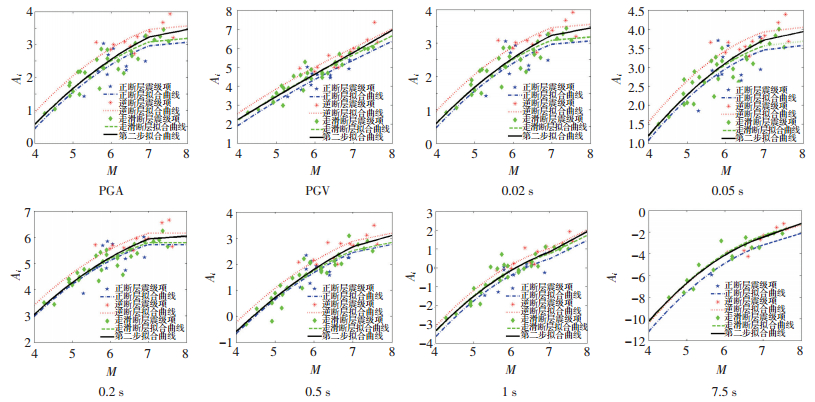
|
图 6 第二步的回归 Figure 6 Stage 2 regression fits |
NGA数据库对上、下盘的范围作了较为详细的规定.在第一步的残差分析中,区分上、下盘记录的观察值和预测值的比值在子源震中距为横坐标的坐标系下的分布见图 7.除长周期,上、下盘地震动并没有明显差别.
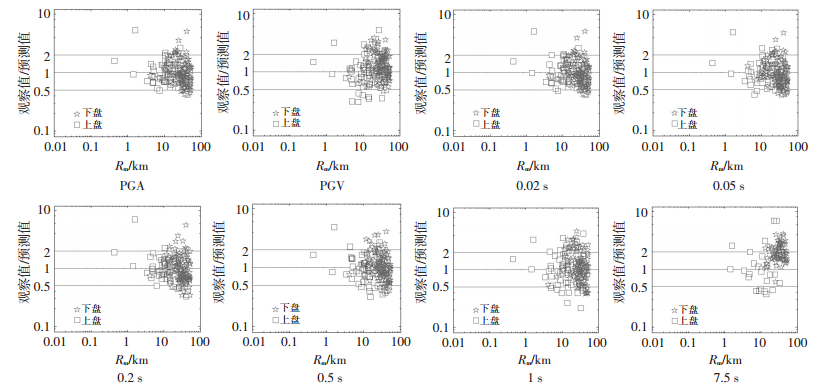
|
图 7 上、下盘效应的影响 Figure 7 Hanging/foot wall effect |
覆盖层厚度被认为是影响地震动的因素之一.图 8是以各台站的覆盖层厚度为横坐标,VS30为纵坐标的分布图 (Z1.5、Z2.5分别为地表到剪切波速1.5 km/s和2.5 km/s岩层的厚度).
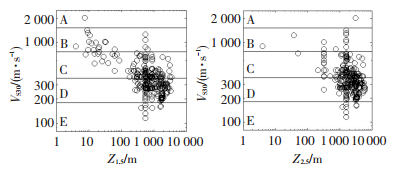
|
图 8 覆盖层厚度与剪切波速之间的关系 Figure 8 Shear wave velocity against basin depth |
从图 8可见,剪切波速和覆盖层厚度之间存在一定的相关性.这种相关性很容易解释:在土层厚度较小时,随着覆盖层厚度的增加VS30的变化较明显;当其增加到一定程度,近地面30 m均为土层,这样VS30就只在土层的范围内变化,与土层的性质有关.因此,覆盖层厚度对地震动的影响与场地条件 (VS30) 的影响存在着某种联系.
为确定覆盖层厚度对地震动影响的大小,以Z1.5为横坐标,第一步观察值与预测值的比值为纵坐标的分布见图 9.从图中可以看到,覆盖层厚度与剪切波速的相关性很明显,但该比值随着覆盖层厚度的变化并未出现明显的规律性差别.
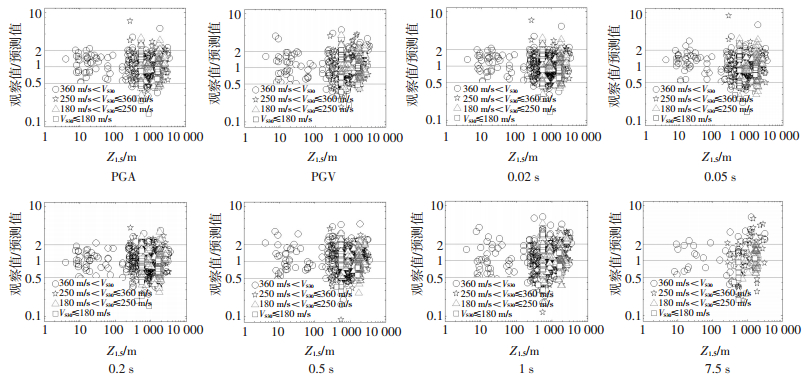
|
图 9 覆盖层厚度的影响 Figure 9 Basin depth effect |
标准差是衡量回归结果是否理想的一个重要因素.本文及BA08[16]模型的回归标准差均与周期相关,图 10为不同周期标准差的两种模型的对比.本文的标准差略大于BA08[16]模型,但差别并不大.两种模型标准差的差别主要是由于对距离参数的定义方式不同造成的.
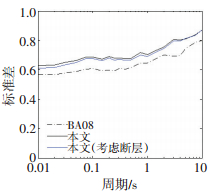
|
图 10 标准差比较 Figure 10 Comparison of standard deviation |
1) 本文利用经验格林函数法合成了集集地震某台站主震的近场时程,结果表明:大震近场地震动主要与离场地较近的那部分断层有关.
2) 结合NGA数据库分析了多圆组合模型中子断层的划分和子源震中距的求法.并拟合出了NGA数据库的多圆组合地震动衰减关系.对拟合结果分析表明:断层类型对地震动有一定的影响;除长周期外,上、下盘的地震动无明显的差别;考虑了场地 (通过土层剪切波速体现) 对地震动的放大作用后,覆盖层厚度对地震动的影响也并不明显;多圆组合模型的拟合标准差稍大于NGA的BA08模型.总的来说,多圆组合模型能较好反映NGA数据库中地震动的衰减趋势.
虽然本文模型与NGA模型在回归精度上有一点差距,但是这种差距在工程上可以忽略.多圆组合模型的距离定义简单,相比NGA模型在地震动预测中应用更加简便.通过对汶川地震峰值加速度的初步研究[12]以及本文对NGA数据库地震动记录的回归分析较为充分地证明了多圆组合模型回归的可靠性.下一步将利用多圆组合模型进行地震动的预测,并将模型与危险性分析相结合从而推动模型的实际应用.
| [1] | KANAI K. An empirical formula for the spectrum of strong earthquake motions[J]. Bull. Eq. Res. Inst, 1961, 39: 85-95. |
| [2] |
王海云, 谢礼立. 近断层强地震动的特点[J].
哈尔滨工业大学学报, 2006, 38(12): 2070-2072, 2076.
WANG Haiyun, XIE Lili. Characteristics of near-fault strong ground motions[J]. Journal of Harbin Institute of Technology, 2006, 38(12): 2070-2072, 2076. DOI: 10.3321/j.issn:0367-6234.2006.12.012 |
| [3] | DER KIUREGHIAN A, ANG A H-S. A fault-rupture model for seismic risk analysis[J]. Bulletin of the Seismological Society of America, 1977, 67(4): 1137-1184. |
| [4] | POWER M, CHIOU B, ABRAHAMSON N, et al. AN overview of the NGA project[J]. Earthquake Spectra, 2008, 24(1): 3-21. DOI: 10.1193/1.2894833 |
| [5] |
沈建文, 华宜平, 邱瑛, 等. 地震危险性分析的经验点椭圆模型[J].
地震学报, 1989, 11(3): 259-267.
SHENG Jianwen, HUA Yiping, QIU Ying, et al. Empirical point-ellipse model for seismic hazard analysis[J]. Acta Seismologica Sinica, 1989, 11(3): 259-267. |
| [6] |
杨帆, 罗奇峰. 四区域椭圆模型的汶川8.0地震加速度峰值衰减关系拟合[J].
振动与冲击, 2010, 29(5): 136-140.
YANG Fan, LUO Qifeng. Wenchuan 8.0 magnitude acceleration peak attenuation curve using four-area elliptical model[J]. Journal of Vibration and Shock, 2010, 29(5): 136-140. |
| [7] |
杨帆, 罗奇峰. 汶川地震的6区域模型加速度峰值衰减关系[J].
土木建筑与环境工程, 2010, 32(5): 29-34.
YANG Fan, LUO Qifeng. Fitting of acceleration peak attenuation with six-area model for Wenchuan 8.0 magnitude earthquake[J]. Journal of Civil Architeetural & Environmental Engineering, 2010, 32(5): 29-34. |
| [8] |
刘平, 罗奇峰. 基于"映射圆"模型的汶川8.0级地震峰值加速度衰减关系[J].
振动与冲击, 2013, 32(3): 75-78.
LIU Ping, LUO Qifeng. Wenchuan 8.0 maginatude earthquake peak acceleration attenuation relationship besed on a model of mapping circle[J]. Journal of Vibration and Shock, 2013, 32(3): 75-78. |
| [9] |
姚振兴, 郑天愉. 近场强地面运动研究[J].
中国地震, 1986, 2(3): 22-30.
YAO Zhenxing, ZHENG Tianyu. Summary of study on near-field ground motion[J]. Earthquake Research in China, 1986, 2(3): 22-30. |
| [10] |
罗奇峰. 近场加速度的半经验合成[D]. 哈尔滨: 国家地震局工程力学研究所, 1989.
LUO Qifeng, The semi-empirical synthesisof near-field ground motions[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 1989. http://d.wanfangdata.com.cn/Thesis/Y129975 |
| [11] |
陈运泰, 杨智娴, 张勇, 等. 从汶川地震到芦山地震[J].
中国科学:地球科学, 2013, 43(6): 1064-1072.
CHEN Yuntai, YANG Zhixian, ZHAGN Yong, et al. From 2008 Wenchuan earthquake to 2013 Lushan earthquake[J]. Scientia Sinica Terrae, 2013, 43(6): 1064-1072. |
| [12] |
刘平, 罗奇峰. 汶川地震峰值加速度多圆组合模型的衰减关系[J].
中南大学学报 (自然科学版), 2015, 46(6): 2317-2323.
LIU Ping, LUO Qifeng. Wenchuan earthquake peak acceleration attenuation relationship of multiple circle model[J]. Journal of Central South University (Science and Technology), 2015, 46(6): 2317-2323. |
| [13] | CHIOU B S, DARRAGH R B, GREGOR N J, et al. NGA Project Strong-Motion Database[J]. Earthquake Spectra, 2008, 24(1): 23-44. DOI: 10.1193/1.2894831 |
| [14] | ABRAHAMSON N, SILVA W. Summary of the Abrahamson & Silva NGA ground-motion relations[J]. Earthquake Spectra, 2008, 24(1): 67-97. DOI: 10.1193/1.2924360 |
| [15] | MARK R K, BONILLA M G. Regression analysis of earthquake magnitude and surface fault length using the 1970 data of Bonilla and Buchanan: USGS open-file report 77-614 [R].Virginia: USGS, 1977. |
| [16] | BOORE D M, ATKINSON G M. Ground-motion prediction equations for the average horizontal component of PGA, PGV, and 5%-damped PSA at spectral periods between 0.01 s and 10.0 s[J]. Earthquake Spectra, 2008, 24(1): 99-138. DOI: 10.1193/1.2830434 |
| [17] |
刘平, 罗奇峰. 考虑样本分布不均的衰减关系的加权两步回归法[J].
地震学报, 2014, 36(4): 711-718.
LIU Ping, LUO Qifeng. Weighted two-step regression method of attenuation relationship considering sample uneven distribution[J]. Acta Seismologica Sinica, 2014, 36(4): 711-718. |
 2017, Vol. 49
2017, Vol. 49


