2. 哈尔滨工业大学 土木工程学院,哈尔滨 150090
2. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China
强地震动衰减是工程地震学的一个重要研究方向.在地震危险性评估中,不管是概率方法还是确定性方法,都需要借助地震动衰减关系估算场地的地震动期望值.大多数衰减关系是经验性的,研究基础是强地震动的观测数据.在美国西部、日本等观测数据丰富的地区,相关研究一直处于前列[1-3].近几年,美国新一代地震动衰减关系项目 (NGA) 取得的进展影响很大[4],最大的贡献是发布了一个当前最丰富的地震动数据库,不仅包括美国和加拿大西部的数据,也包括中国台湾、土耳其、中国大陆、伊朗、意大利、墨西哥、新西兰以及日本等国家和地区的强震记录[5].此举曾使人产生错觉,以为在全球数据的基础上,有可能建立全球适用的衰减关系.虽然NGA考虑得更加全面,参数增加很多,成果也鼓励世界上其他地区试用,但项目的成果以NGA-West命名,说明这类关系肯定是区域性的,美国中东部仍然需要另外研究衰减关系,NGA-East就是最有力的证明.从道理上说,区域的地壳结构、地壳介质动力性质及震源机制的不同都会影响地震动衰减规律,世界上大多数国家或地区尚缺少足够的强地震动观测数据,难以直接建立经验性的衰减关系.在中国,对观测数据丰富地区统计结果进一步修正的作法得到广泛应用[6-7],亦受到一些质疑[8-9].与此同时,其他国家的地震学者发展了基于随机振动理论的简化方法[1, 10-12].十多年来,中国研究人员陆续有相关论文发表[13-16].本文是在这些相关研究进展基础上的一个总结推进.
1 从基于随机振动理论到基于地震学的强地震动衰减关系基于随机振动理论的方法,用震源谱表达震源对地震动的影响,用几何衰减和非弹性衰减项表达传播途径对地震动的影响,用场地放大和高频截止项表达局部场地条件对地震动的影响,比经验性衰减关系中只用震级一个参数、一个综合衰减项和一个场地分类项表达这三方面的影响,更全面,更突出强调物理意义[9, 15, 17].
| $ \begin{array}{l} {F_{\rm{A}}}\left( {{M_0},f,R} \right) = C \cdot S\left( {{M_0},f} \right) \cdot G\left( R \right) \cdot D\left( {R,f} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;A\left( f \right) \cdot P\left( f \right) \cdot I\left( f \right). \end{array} $ | (1) |
式中:M0为地震矩,f为频率,R为震源距,C为比例系数,可参照震源附近地壳介质密度和剪切波速取值,S(M0, f) 为震源谱,描述从震源辐射的总能量大小和能量在频域的分布,G(R) 为几何衰减项,描述几何扩散导致的地震动衰减,D(R, f) 为非弹性衰减项,描述地震波传播过程中地壳介质耗散能量引起的地震动衰减,A(f) 为近地表幅值放大因子,描述近地表地壳的速度梯度变化对地震动的影响,P(f) 为近地表高频截止项,描述近地表地震动中不含有很高频率成分的现象,I(f)=(2πf)z中分别取z=0、1或2,表达地震动位移和速度、加速度的关系.
应用最广泛的震源谱是Brune[19-20]提出的ω2模型.为避免合成大地震的地震动中子源尺寸对地震动的影响,作者课题组借鉴Masuda[21]的谱形提出如下改进[13, 22]:
| $ S\left( {{M_0},f} \right) = \frac{{{M_0}}}{{{{\left[ {1 + {{\left( {\frac{f}{{{f_0}}}} \right)}^a}} \right]}^b}}}. $ | (2) |
式中:f为频率,f0为拐角频率,a、b是同震级有关的系数,a=3.05-0.33Mw,b=2.0/a.
| $ {f_0} = 4.9 \times {10^6}{\beta _{\rm{s}}}{\left( {\Delta \sigma /{M_0}} \right)^{1/3}}. $ | (3) |
式中Δσ为应力降,描述地壳应力在地震后相比地震前的降低,不能直接测量,可借助远场记录反演估计.一般认为,Δσ与地震破裂面上的错动成正比,同破裂面的大小成反比.大多数研究者认为大地震的应力降是基本稳定的,对小地震的应力降尚有不同的观点.Shearer[23]研究论证应力降呈区域性.
几何衰减项G(R) 可以分不同的距离段定义,分别反映近距离处地震动成分以体波 (剪切波) 为主、远距离处以面波为主以及两者之间的一段距离上直达波与来自莫霍面临界反 (折) 射波叠加形成的地震动衰减缓慢甚至基本不衰减 (称为地壳波导效应) 的不同特征.几何衰减项与区域地壳速度结构有密切关系,通常用三段函数表示[12].
| $ G\left( R \right) = \left\{ \begin{array}{l} \frac{1}{R},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;R \le {R_1};\\ \frac{1}{{{R_1}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{R_1} \le R \le {R_2};\\ \frac{1}{{{R_1}}}\sqrt {\frac{{{R_2}}}{R}} ,\;\;\;\;\;\;\;\;\;\;\;{R_2} \le R. \end{array} \right. $ | (4) |
式中R1和R2为距离分段点.
非弹性衰减项D(R, f) 可表达为[18]
| $ D\left( {R,f} \right) = {{\rm{e}}^{ - \frac{{\pi fR}}{{Q\beta }}}}, $ | (5) |
式中Q为品质因子,其值越大,地震波的衰减越慢,可表达为
| $ Q = {Q_0}{f^\eta }, $ | (6) |
式中Q0为f=1 Hz的品质因子,η为常数.
近地表幅值放大因子A(f) 可以根据区域地壳速度结构按四分之一波长法近似确定[24].一般认为,近地表高频截止项P(f) 描述的是传播路径和场地效应,或是这两种效应与震源效应的综合.普遍使用的有fmax滤波器和kappa滤波器,分别表达为[25-26]:
| $ P\left( f \right) = {\left[ {1 + {{\left( {\frac{f}{{{f_{\max }}}}} \right)}^8}} \right]^{ - 1/2}}, $ | (7) |
| $ P\left( f \right) = {{\rm{e}}^{ - \pi f\kappa }}. $ | (8) |
式中fmax为地震动高频截止频率,κ称为“kappa”系数,一般认为与距离和场地条件密切相关.
大地震近场地震动可以借助有限断层震源模型合成,此处不详述.
由上述可知,地震动傅里叶幅值谱的估计中,震源谱中的应力降Δσ、品质因子Q中的Q0和η以及几何衰减项的两个分段点距离R1和R2等5个区域性参数,分别控制了近场地震动的强度和随距离衰减的速率,通常多不能直接量测到.不同研究成果采用的基本数据,甚至公式的形式往往不同,结果差别不小,直接采用随机性过大,对地震学研究基础相对薄弱的地区更不可靠.为克服这一瓶颈,与地震研究者对其中某些参数反演研究的思路相类似[27-29],本文作者提出、发展了根据宽频带数字地震监测台网的小震记录,借助遗传算法对这5个参数联合反演估值的方法[30-31].
遗传算法是一种启发式的、有指导的蒙特卡洛反演方法,全局搜索能力强,不需要计算目标函数的导数,可以解决复杂的大尺度、多变量非线性反演问题.作者采用的微遗传算法是传统遗传算法的一种改进,便于在较小的种群中得到较好的优化结果,应用很广泛.先从一组随机数中进行初始化操作产生个体,计算每个个体的适应度;再通过锦标赛选择、精英策略和交叉操作产生新个体;通过判断种群收敛性确定是否重复以上步骤;在所有的代数中,寻求适应度最大的数值组合个体作为最终结果[32].
反演中,一般选用震级在3.5~4.5之间的数十次区域浅源构造地震中几十个数字测震台站记录到的上百或几百条速度时程.以相应傅里叶幅值谱或其包络线与按式 (1) 中I(f) 取2πf、根据震级推算的地震矩及选定的一组5个区域参数计算得到的速度傅里叶幅值谱贴近为目标,构造目标函数:
| $ {\varphi _j} = \sum\limits_{k = 1}^N {\sum\limits_{i = 1}^{4\;096} {{{\left[ {{F_{{A_0}}}\left( {i,k} \right) - {F_{{A_j}}}\left( {i,k} \right)} \right]}^2}} } . $ | (9) |
式中:N为小震记录的总数,FA0(i, k) 为第k个记录的傅里叶幅值谱 (离散成4 096个点) 的第i个幅值,FAj(i, k) 为据第k个记录对应的震级、距离和第j代5个区域参数值,按式 (1) 计算得到的傅里叶幅值谱的第i个幅值.采用式 (10),可以将适应度压缩至 (0, 1].
| $ {F_j} = \exp \left( { - \beta {\varphi _j}} \right), $ | (10) |
式中β为适应度变换系数.进一步设计反演策略,就可以在给定的相当宽泛的取值域中搜索寻优,得到合适的参数值.如此,既扩展了丰富的数据源,又与地震学密切结合,体现了区域特征.
给定一组M0和R,将上述区域参数分别代入式 (3)~(5),借助式 (1) 估计得到地震动的加速度傅里叶幅值谱后,可以据其与功率谱的关系,以及功率谱零阶谱矩m0的定义,按式 (11) 计算其值.
| $ {m_0} = 2\int\limits_0^\infty {{{\left| {{F_A}\left( f \right)} \right|}^2}{\rm{d}}f} . $ | (11) |
由Parseval定理,加速度均方根值Arms可表示为
| $ {A_{{\rm{rms}}}} = {\left( {\frac{{{m_0}}}{{{T_{\rm{d}}}}}} \right)^{1/2}}, $ | (12) |
式中Td为强烈震动段的持续时间.综合考虑震源辐射模式和台站方位效应、自由地表放大效应及地震动能量的水平分量后,还要再乘上一个系数0.85[3, 33].
均方根值Arms乘以峰值因子γm[34],可得到相应加速度峰值PGA.
| $ {\gamma _{\rm{m}}} = 2\int\limits_0^\infty {\left\{ {1 - {{\left[ {1 - \xi \exp \left( { - {z^2}} \right)} \right]}^{{N_{\rm{e}}}}}} \right\}{\rm{d}}z} . $ | (13) |
式中:ξ为带宽因子,描述随机变量的分布形式,
按上述方法得到地震动衰减关系是基于随机振动理论.推导中,式 (13)(称为峰值因子) 的推导,均是以平稳随机过程理论为基础的,用于强烈非平稳的地震动时程,即便是只考虑相对平稳的强烈震动段亦颇受质疑.作者课题组随后的研究表明,采用这种简化会导致误差增加10%~15%[35],没有必要为节约不很多的计算时间而付出准确性的代价.可以利用地震动的傅里叶幅值谱和一个随机相位谱结合直接生成时程,从中读取峰值,取不同相位谱多次合成时程的峰值平均值作为期望值,故改称为基于地震学的地震动衰减关系[36].
2 建立基于地震学的强地震动峰值衰减关系的3个实例上述思路先在数据丰富的地区研究验证,是方法发展与推广应用不可缺少的一个环节,本文介绍的第一个实例就选在日本东北地区.随后,在中国积累有一些强地震动记录的川滇地区试用,进一步与区域强地震动观测的数据比较,即便是不够充分的数据,亦可在一定程度上说明本文方法的适用性.
2.1 例1区域范围取东经138°~143°、北纬36°~40°.小震数据取自宽频带数字地震台网F-net (www.fnet.bosai.go.jp) 的12个台站,1996年1月至2010年10月间,震源深度不大于30 km的632次小地震 (Mw=3.5~4.5) 的850条记录.检验用的强地震动数据取自K-NET (www.kyoshin.bosai.go.jp) 的89个基岩台站,在同一时间段187次地震 (Mw≥4.5) 的4 323条观测记录.
参考区域地震学研究成果,选定Δσ、Qo、η、R1、R2等5个参数的可能取值范围,用微遗传算法反演得到满意的解,列于表 1[35].将反演结果代入式 (3)~(5),对一系列M和R,按式 (1) 计算傅里叶幅值谱,再进一步借助式 (11) 和式 (12) 计算地震动均方根加速度值,与峰值因子相乘,得到地震动峰值加速度衰减的结果.
| 表 1 日本东北地区的参数反演搜索范围和得到的区域参数值 Table 1 Ranges and results of the inversion in northeastern Japan |
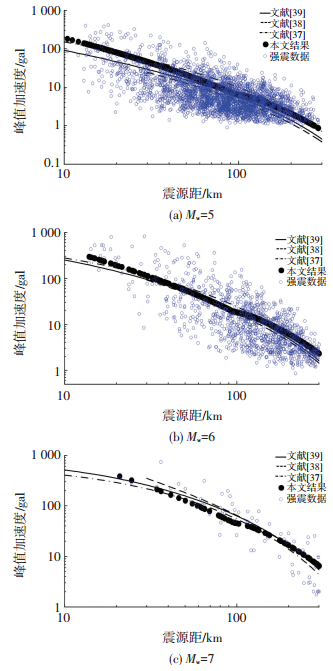
为了比较、检验,图 1中分别表示了5、6、7级地震的PGA衰减的结果 (实心点) 和相应震级±0.5范围内的强地震动观测数据 (小圈),以及日本学者发表的3组用强地震动观测数据统计回归建立的区域经验性衰减关系[37-39].
|
图 1 PGA衰减曲线与观测数据的比较 (例1) Figure 1 Comparison of PGA attenuation relations with observed data (Example 1) |
从图 1可见,本文完全根据小地震的速度记录反演区域参数,一条强地震动数据都没有用,得到的结果与强地震动观测数据符合得很好,与日本学者统计得到的经验性衰减关系大体相同.
2.2 例2区域范围选择四川省.小震数据取自区域地震观测台网29个数字台站,2001年初至2007年底之间,震源深度不大于30 km的82次小地震 (Mw=3.5~4.5) 的147条记录.检验用的强地震动数据取自中国地震局工程力学研究所“国家强震动台网中心”,选择同一时空范围内强震台网69个台站记录到的118次地震 (Mw≥4.5) 的1237条数据.参考区域地震学研究成果,选取的参数反演搜索范围和得到的区域参数值,列于表 2[40].
| 表 2 四川的参数反演搜索范围和得到的区域参数值 Table 2 Ranges and results of the inversion in Sichuan region |
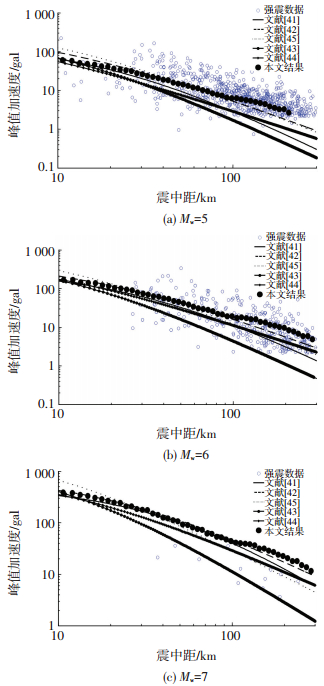
据此建立的衰减关系与区域有限的强地震动数据 (主要是汶川地震余震的记录),见图 2.图中分别表示了5、6、7级地震的PGA结果和相应震级±0.5范围内的强地震动观测数据,以及5组区域通常使用的衰减关系曲线[41-45].为便于比较,凡分别长、短轴方向给出衰减关系的,距离均折算为等效圆半径.
|
图 2 PGA衰减曲线与观测数据的比较 (例2) Figure 2 Comparison of PGA attenuation relations with observed data (Example 2) |
从图 2可见,对应5、6级地震的衰减曲线从数据点丛中间穿过,上下两侧数据点的分布比较均匀,“盲测”成功.对于7级地震,本文方法的结果显得衰减慢些,在100 km以上的距离处高于观测值,是观测数据不足,还是其他问题有待进一步研究.
2.3 例3区域范围取云南省.小震数据取自区域地震观测台网26个数字台站,2001年初至2007年底之间,震源深度不大于30 km的154次小地震 (Mw=3.5~4.5) 的863条记录.检验用的强地震动数据取自国家强震动台网36个台站,同一时空范围内27次地震 (Mw≥4.5) 的78条记录.参数反演搜索范围和得到的区域参数值,列于表 3[40].
| 表 3 云南的参数反演搜索范围和得到的区域参数值 Table 3 Ranges and results of the inversion in Yunnan region |
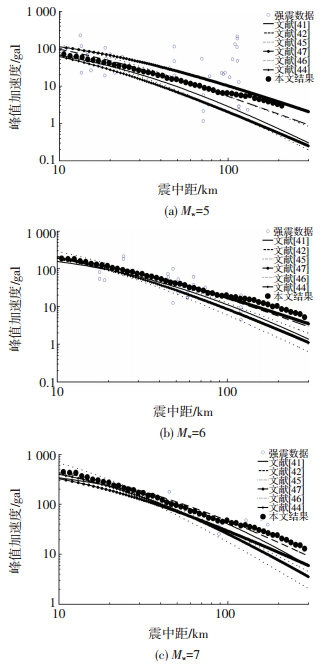
采用同样方法建立区域衰减关系与区域有限的强地震动数据,见图 3.分别表示了5、6、7级地震的PGA结果和相应震级±0.5范围内的强地震动观测数据,以及6组区域通常使用的衰减关系曲线[41-42, 44-47].
|
图 3 PGA衰减曲线与观测数据的比较 (例3) Figure 3 Comparison of PGA attenuation relations with observed data (Example 3) |
从图 3可见,结果与观测数据亦很匹配,观测数据点较为分散,曲线从中穿过.与区域通常使用的衰减关系相比,在100 km以内没有明显差别,在更远处本文的结果显得衰减偏慢,是否合理还有待观测数据积累来检验.
3 结语世界上大多数国家或地区都缺少足够的强地震动观测数据,难以直接统计建立经验性地震动衰减关系.本文在作者十几年研究基于地震学的强地震动衰减关系的基础上,讨论了从基于随机振动理论的简化方法向基于地震学的地震动衰减的发展,详细介绍了借助地震监测台网的小震数据反演区域震源谱和衰减参数的技术途径.通过3个研究实例说明据此估计的地震动与区域 (有限的) 强地震动观测的数据比较,说明了方法的适用性.对于5、6级地震,两者相符;对于7级地震,在强地震动数据丰富的日本东北地区符合得很好,对强地震动数据有限的中国川滇地区在距离大于100 km的距离处符合得不够好,是观测数据不足,还是其他方面的问题,有待进一步研究.
| [1] | AKI K. Attenuation of shear-waves in the lithosphere for frequencies from 0.05 to 25 Hz[J]. Physics of the Earth and Planetary Interiors, 1980, 21: 50-60. DOI: 10.1016/0031-9201(80)90019-9 |
| [2] | BOORE D M. Stochastic simulation of high-frequency ground motions based on seismological models of the radiated spectra[J]. Bulletin of the Seismological Society of America, 1983, 73(6): 1865-1894. |
| [3] | ATKINSON G M. Attenuation of strong ground motion in Canada from a random vibrations approach[J]. Bulletin of the Seismological Society of America, 1984, 74(6): 2629-2653. |
| [4] | POWER M, CHIOU B, ABRAHAMSON N, et al. An overview of the NGA project[J]. Earthquake Spectra, 2008, 24(1): 3-21. DOI: 10.1193/1.2894833 |
| [5] | ANCHETA T D, BOZORGNIA Y, DARRAGH R, et al.PEER NGA-west2 database: a database of ground motions recorded in shallow crustal earthquakes in active tectonic regions [C]// Proc 12th World Conf Earthquake Engineering.Auckland, New Zealand: New Zealand Society for Earthquake Engineering, 2000: No.5599. |
| [6] |
胡聿贤, 张敏政. 缺乏强震观测资料地区地震动参数的估算方法[J].
地震工程与工程振动, 1984, 4(1): 1-11.
HU Yuxian, ZHANG Minzheng. A method of predicting ground motion parameters for regions with poor ground motion data[J]. Earthquake Engineering and Engineering Vibration, 1984, 4(1): 1-11. |
| [7] |
胡聿贤, 周克森, 闫秀杰. 缺乏地震动加速度记录地区地震动估计的映射法[J].
地震工程与工程振动, 1996, 16(3): 1-10.
HU Yuxian, ZHOU Kesen, YAN Xiujie. A method for evaluation of ground motion in regions with few acceleration observationdata[J]. Earthquake Engineering and Engineering Vibration, 1996, 16(3): 1-10. |
| [8] |
王亚勇, 刘小弟, 黎家佑, 等. 澜沧-耿马强震地面运动特征研究[J].
地震工程与工程振动, 1991, 11(2): 11-19.
WANG Yayong, LIU Xiaodi, LI Jiayou, et al. Research on strong ground motion of Lanchang-Gengma Earthquake[J]. Earthquake Engineering and Engineering Vibration, 1991, 11(2): 11-19. |
| [9] |
陶夏新, 李小军. 工程地震基本科学问题-学科发展战略研究报告 (2006年—2010年), 建筑、环境与土木工程Ⅱ(土木工程卷)[R]. 国家自然科学基金委员会工程与材料科学部. 北京: 科学出版社, 2006.
TAO Xiaxin, LI Xiaojun.Fundamental scientific issues on engineering seismology-Report of strategy research on discipline development (2006—2010), architecture, environment and civil engineering Ⅱ (volume of civil engineering) [R].National Natural Science Foundation of China.Beijing: Science Press, 2006. |
| [10] | HANKS T C. b values and ω-γ source models: implications for tectonic stress variations along active crustal fault zones and the estimation of high-frequency strong ground motion[J]. Journal of Geophysical Research, 1979, 84(B5): 2235-2242. DOI: 10.1029/JB084iB05p02235 |
| [11] | MCGUIRE R K, HANKS T C. RMS accelerations and spectral amplitudes of strong ground motion during the San Fernando, California Earthquake[J]. Bulletin of the Seismological Society of America, 1980, 70(5): 1907-1919. |
| [12] | ATKINSON G M, BOORE D M. Ground motion relation for Eastern North America[J]. Bulletin of the Seismological Society of America, 1995, 85(1): 17-30. |
| [13] |
王国新. 强地面运动衰减研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2001.
WANG Guoxin.Strong ground motion attenuation[D].Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2001. |
| [14] |
黄玉龙, 郑斯华, 刘杰, 等. 广东地区地震动衰减和场地响应的研究[J].
地球物理学报, 2003, 46(1): 54-61.
HUANG Yulong, ZHENG Sihua, LIU Jie, et al. Attenuation of ground motion and site response in Guangdong region[J]. Chinese Journal of Geophysics, 2003, 46(1): 54-61. |
| [15] | TAO Z R, TAO X X, LIU C.Strong ground motion attenuation estimation from random vibration approach [C]// Proc of International Conf Earthquake Engineering and Disaster Mitigation.Indonesia: IEEA, 2008: No.024. |
| [16] | TAO Z R, TAO X X, LIU C.Strong ground motion attenuation estimation approach in Southeast of China [C]// Proc of 4th International Conf Advances in Structural Engineering and Mechanics.Korea: Korea Advanced Institute of Science & Technology, 2008: 3306-3316. |
| [17] | SOMERVILLE P.Seismic hazard evaluation [C]// Proc of 12th World Conf Earthquake Engineering.Auckland, New Zealand: New Zealand Society for Earthquake Engineering, 2000: No.2833. |
| [18] | HANKS T C, MCGUIRE R K. The character of high frequency strong ground motion[J]. Bulletin of the Seismological Society of America, 1981, 71(6): 2071-2095. |
| [19] | BRUNE J N. Tectonic stress and the spectra of seismic shear waves from earthquake[J]. Journal of Geophysical Research, 1970, 75(26): 4997-5009. DOI: 10.1029/JB075i026p04997 |
| [20] | BRUNE J N. Correction[J]. Journal of Geophysical Research, 1971, 76(20): 5002. DOI: 10.1029/JB076i020p05002 |
| [21] | MASUDA T.Scaling relations for source parameters of microearthquakes in the Northeastern part of Japan[D].Tohoku: Tohoku University, 1982. |
| [22] | TAO X X, SUN X D, WANG G X.A dynamic corner frequency based source spectral model [C]// Proc of 14th World Conf Earthquake Engineering.Beijing: Chinese Association of Earthquake Engineering, 2008: S02004. |
| [23] | SHEARER P M. Introduction to Seismology[M]. 2nd ed. London: Cambridge University Press, 2009. |
| [24] | BOORE D M, JOYNER W B. Site amplification for generic rock sites[J]. Bulletin of the Seismological Society of America, 1997, 87(2): 327-341. |
| [25] | ANDERSON J G, HOUGH S E. A model for the shape of the Fourier amplitude spectrum of acceleration at high frequencies[J]. Bulletin of the Seismological Society of America, 1984, 74(5): 1969-1993. |
| [26] | HANKS T C. fmax[J]. Bulletin of the Seismological Society of America, 1982, 72(5): 1867-1879. |
| [27] |
刘杰, 郑斯华, 黄玉龙. 利用遗传算法反演非弹性衰减系数、震源参数和场地效应[J].
地震学报, 2003, 25(2): 211-218.
LIU Jie, ZHENG Sihua, HUANG Yulong. The inversion of non-elasticity coefficient, source parameters, site response using genetic algorithms[J]. ACTA Seismologica Sinica, 2003, 25(2): 211-218. |
| [28] |
姜慧, 胡聿贤, 赵凤新, 等. 用随机模拟方法研究设定地震地面运动[J]. 地球物理学报, 2007, 50(3): 823-829.
JIANG Hui, HU Yuxian, ZHAO Fengxin, et al.Study on the ground motion of scenario earthquake using stochastic simulation method[J].Chinese Journal of Geophysics, 50(3): 823-829. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=dqwx200703021&dbname=CJFD&dbcode=CJFQ |
| [29] |
温瑞智, 王宏伟, 任叶飞, 等. 芦山余震震源参数及震源区品质因子反演[J].
哈尔滨工业大学学报, 2015, 47(4): 58-63.
WEN Ruizhi, WANG Hongwei, REN Yefei, et al. Estimation of source parameters and quality factor based on generalized inversion method in Lushanearthquake[J]. Journal of Harbin Institute of Technology, 2015, 47(4): 58-63. DOI: 10.11918/j.issn.0367-6234.2015.04.010 |
| [30] | TAO Z R.Ground motion attenuation relationship based on stochastic method[D].Tokyo: National Graduate Institute for Policy Studies and Building Research Institute, 2010. |
| [31] | TAO Z R, CUI A P, WANG X W, et al.Inversion strategy for seismic source and regional parameters [C]// Proc of 8th International Conf Natural Computation.Chongqing, China: Chongqing University of Posts and Telecommunications, 2012: 675-678. |
| [32] | CARROLL D L.FORTRAN genetic algorithm (GA) driver [EB/OL].(2001-04-02)[2009-04-15].http://cuaerospace.com/carroll/ga.html. |
| [33] |
刘陶钧. 基于加利福尼亚区域参数的地震动衰减[D]. 哈尔滨: 哈尔滨工业大学, 2009.
LIU Taojun.Ground motion attenuation relationship from the regional parameters of California[D].Harbin: Harbin Institute of Technology.2009. |
| [34] | CARTWRIGHT D E, LONGUET-HIGGINS M S. The statistical distribution of the maxima of a random function[J]. .Proceedings of the Royal Society of London.Series A, Mathematical and Physical Sciences, 1956, 237(1209): 212-223. DOI: 10.1098/rspa.1956.0173 |
| [35] |
王希伟. 基于地震学的日本东北地区地震动衰减关系研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2012.
WANG Xiwei.Seismology based ground motion attenuation relationship for Tohoku area[D].Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2012. http://cdmd.cnki.com.cn/Article/CDMD-85406-1012411113.htm |
| [36] | BOORE D M. Simulation of ground motion using the stochastic method[J]. Pure and Applied Geophysics, 2003, 160: 635-676. DOI: 10.1007/PL00012553 |
| [37] | FUKUSHIMA Y, TANAKA T. A new attenuation relation for peak horizontal acceleration of strong ground motion in Japan[J]. Bulletin of the Seismological Society of America, 1990, 80(4): 757-783. |
| [38] | SI H, MIDORIKAWA S.New attenuation relations for peak ground acceleration and velocity considering effects of fault type and site condition [C]// Proc of 12th World Conf Earthquake Engineering.Auckland, New Zealand: New Zealand Society for Earthquake Engineering, 2000: No.0532. |
| [39] | KANNO T, NARITA A, MORIKAWA N, et al. A new attenuation relation for strong ground motion in Japan based on recorded data[J]. Bulletin of the Seismological Society of America, 2006, 96(3): 879-897. DOI: 10.1785/0120050138 |
| [40] |
崔安平. 用地震观测台网的小震记录建立川滇强地震动衰减关系[D]. 哈尔滨: 中国地震局工程力学研究所, 2013.
CUI Anping.Strong ground motion attenuation relationship for Sichuan-Yunnan region from small earthquake records by China earthquake networks[D].Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2013. http://cdmd.cnki.com.cn/Article/CDMD-85406-1013342693.htm |
| [41] |
中国地震动参数区划图: GB 18306—2001[S]. 北京: 中国标准出版社, 2001.
Seismic ground motion parameter map of Chin: GB 18306—2001[S].Beijing: Standards Press of China, 2001. |
| [42] |
俞言祥, 汪素云. 中国东部和西部地区水平向基岩加速度反应谱衰减关系[J].
震灾防御技术, 2006, 1(3): 206-217.
YU Yanxiang, WANG Suyun. Attenuation relations for horizontal peak ground acceleration and response spectrum in Eastern and Western China[J]. Technology for Earthquake Disaster Prevention, 2006, 1(3): 206-217. DOI: 10.11899/zzfy20060304 |
| [43] |
蔡辉腾, 李英民, 郑清, 等. 重庆及邻近地区水平向基岩地震动加速度峰值与反应谱衰减关系[J].
四川地震, 2007(2): 11-15.
CAI Huiteng, LI Yingmin, ZHENG Qing, et al. Attenuation relations for acceleration peak and response spectrum of horizontal earthquake motions in Chongqing and its adjacent region[J]. Earthquake Research in Sichuan, 2007(2): 11-15. |
| [44] |
雷建成, 高孟潭, 俞言祥. 四川及邻区地震动衰减关系[J].
地震学报, 2007, 29(5): 500-511.
LEI Jiancheng, GAO Mengtan, YU Yanxiang. Seismic motion attenuation relations in Sichuan and adjacent areas[J]. ACTA Seismologica Sinica, 2007, 29(5): 500-511. |
| [45] | CUI J W, ZHANG J G, GAO D, et al.The ground motion attenuation relation for the mountainous area in Sichuan and Yunnan [C]// Proc of 15th World Conf Earthquake Engineering.Lisbon, Portugal: International Association for Earthquake Engineering, 2012. |
| [46] |
崔建文, 李世成, 高东, 等. 云南分区地震动衰减关系[J].
地震研究, 2006, 29(4): 386-391.
CUI Jianwen, LI Shicheng, GAO Dong, et al. Ground motion attenuation relation in the Yunnan area[J]. Journal of Seismological Research, 2006, 29(4): 386-391. |
| [47] |
向建光, 高东. 云南地区基岩水平峰值加速度衰减规律[J].
中国地震, 1992, 8(3): 12-18.
XIANG Jianguang, GAO Dong. The attenuation law of horizontal peak acceleration on the basement rock site in Yunnan area[J]. Earthquake Research in China, 1992, 8(3): 12-18. |
 2017, Vol. 49
2017, Vol. 49


