一些结构在使用过程中会受到循环荷载的作用,例如,铁路桥梁在列车通过时,建筑物受到风荷载作用时,潜艇多次潜入水下和浮出水面时.对这些结构进行受力分析以及可靠性、安全性和疲劳寿命评估时,既需要通过实验来研究循环加载条件下材料的力学行为,也需要建立本构模型来描述这些行为.
材料在循环荷载作用下将产生塑性变形随循环周次逐渐累积的现象,即棘轮行为.对金属材料单轴棘轮现象的模拟,有很多文献进行过报道.Mroz多面模型中,每个屈服面对应有恒定的塑性模量,文献[1-2]指出这种形式的Mroz多面模型不能预测比例加载下的棘轮效应.文献[3-4]在两面模型中提出了新的运动硬化准则,侧重针对比例和非比例应变路径下的循环加载进行模拟.文献[5]首先对chaboche模型[6]、Ohno and Wang模型[7]和Mcdowell模型[8]等几种本构模型进行了评价,之后基于chaboche模型[6, 9],提出了新的运动硬化准则.该文中所有模型的主要区别在于运动硬化准则的不同,这类模型采用了若干分项叠加的运动硬化准则,
参数繁多,部分模型的预测结果和实验结果有较大差异.文献[10-11]应用Tseng-Lee两面模型模拟材料受到定平均值或定幅值循环荷载作用下的力学行为.计算结果表明,对定平均值的情况,当材料参数适用于较小应力幅值的循环加载时,若用来计算较大幅值循环加载时的材料响应,则产生的误差较大;反之也如此.对定幅值的情况也存在上述类似问题,这说明模型还需要改进.文献[11]研究了修正的边界面模型,先建立边界面上对偶点处的塑性模量,通过约束随动中心的运动方向来保证屈服面与边界面只能相切,此模型形式上不够直观、简洁.
本文以边界面模型为基础,建立一种三面本构模型,即一套边界面模型和一套单个屈服面模型的结合,对金属材料在单轴循环加载条件下的力学行为进行模拟,并与前人的实验结果进行比较.
1 本构模型的建立本文研究对象为金属稳定材料,其特征是材料在受到平均值和幅值都固定的循环应变作用时,随着循环周数增加,名义应力幅值σa变化不大且很快趋于稳定.本文建模时,假设:材料的不可逆响应与时间无关;受力变形过程中材料的温度不发生改变.
1.1 应力-应变增量关系应变增量的叠加法则为
| $ {\rm{d}}{\mathit{\boldsymbol{\varepsilon }}_{ij}} = {\rm{d}}\mathit{\boldsymbol{\varepsilon }}_{ij}^e + {\rm{d}}\mathit{\boldsymbol{\varepsilon }}_{ij}^p, $ | (1) |
弹性部分应用胡克定律有
| $ {\rm{d}}\mathit{\boldsymbol{\varepsilon }}_{ij}^e = {\rm{d}}{\mathit{\boldsymbol{s}}_{ij}}/\left( {2G} \right) + {\rm{d}}p/\left( {3K} \right){\mathit{\boldsymbol{\delta }}_{ij}}. $ | (2) |
式中:dεij、dεije、dεijp分别为总应变增量、弹性应变增量和塑性应变增量;dsij为偏应力增量;dσij为正应力增量,dp=dσtt/3为平均应力增量 (t=1, 2, 3);G、K分别为剪切模量和体积模量;δij为Kronecker张量; dεijp由应力空间的流动法则确定,将在后续章节中描述.
1.2 模型的本构方程本文认为材料内部有两种塑性机制,两种机制对应的塑性应变分别记为εijp(1)和εijp(2),材料的总塑性应变为
| $ \mathit{\boldsymbol{\varepsilon }}_{ij}^p = \mathit{\boldsymbol{\varepsilon }}_{ij}^{p\left( 1 \right)} + \mathit{\boldsymbol{\varepsilon }}_{ij}^{p\left( 2 \right)}. $ | (3) |
第一种塑性机制对应于一套边界面模型,包含一个边界面和一个屈服面,对应变量和函数使用的编号为1;第二种塑性机制对应于一套单个屈服面模型,包含有一个屈服面,没有边界面,对应的编号为2.
某些情况下一个边界面模型模拟时有一定困难,再叠加一个屈服面模型可增加模型模拟的灵活度和选择性.
边界面模型中的塑性模量通常是直接给出的,其计算与运动硬化准则无关.本文考虑的边界面模型, 其塑性模量由硬化准则、流动法则和一致性条件得出.
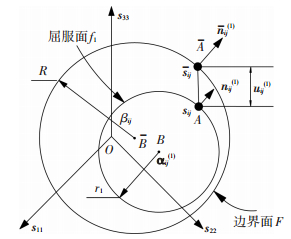
1.2.1 塑性变形1的相关方程塑性变形1及其相关量的描述采用边界面模型.模型包含一个由f1=0决定的屈服面和一个由F=0决定的边界面,它们与偏平面的交线见图 1.设屈服函数f1和边界面函数F的形式为:
| $ {f_1} = \left( {{\mathit{\boldsymbol{s}}_{ij}} - \mathit{\boldsymbol{\alpha }}_{ij}^{\left( 1 \right)}} \right)\left( {{\mathit{\boldsymbol{s}}_{ij}} - \mathit{\boldsymbol{\alpha }}_{ij}^{\left( 1 \right)}} \right) - {\left( {{r_1}} \right)^2}, $ | (4) |
| $ F = \left( {{{\mathit{\boldsymbol{\bar s}}}_{ij}} - {\mathit{\boldsymbol{\beta }}_{ij}}} \right)\left( {{{\mathit{\boldsymbol{\bar s}}}_{ij}} - {\mathit{\boldsymbol{\beta }}_{ij}}} \right) - {R^2}. $ | (5) |
式中:sij为偏应力张量,sij是sij在边界面上的对偶应力;αij(1)和r1分别为偏应力空间中屈服面的圆心和半径;βij和R分别为偏应力空间中边界面的圆心和半径. αij(1)、r1、βij和R都是塑性内变量,其变化规律用微分方程描述,这些方程称为演化方程.
|
图 1 偏平面下屈服面f1=0与边界面F=0的示意 Figure 1 Schematic illustration of yield and bounding surface in deviatoric stress space |
在图 1中,屈服面上的A点为当前应力点,边界面上的A为A点的映射点.根据边界面理论的映射规则,A点处屈服面的法线方向与A点处边界面的法线方向应该相同,故A点法线单位向量nij(1)与A点法线单位向量nij(1)之间存在nij(1)=nij(1).
图 1中各点之间连线存在矢量关系:
| $ \mathit{\boldsymbol{A\bar A = }}\left( {\mathit{\boldsymbol{O\bar B + \bar B\bar A}}} \right) - \left( {\mathit{\boldsymbol{OB + BA}}} \right). $ | (6a) |
设uij(1)为对应于AA的量,βij为对应于OB的量,αij(1)为对应于OB的量,R为矢量
| $ \mathit{\boldsymbol{u}}_{ij}^{\left( 1 \right)} = {{\mathit{\boldsymbol{\bar s}}}_{ij}} - {\mathit{\boldsymbol{s}}_{ij}} = \left( {{\mathit{\boldsymbol{\beta }}_{ij}} - \mathit{\boldsymbol{\alpha }}_{ij}^{\left( 1 \right)}} \right) + \left( {R - {r_1}} \right)\mathit{\boldsymbol{n}}_{ij}^{\left( 1 \right)}, $ | (6b) |
式中uij(1)为当前应力点与边界面上映射点之间的距离.
本文研究的对象是循环稳定材料,相应的r1、R应该取为常数,所以:
| $ {\rm{d}}{r_1} = 0, $ | (7) |
| $ {\rm{d}}R = 0. $ | (8) |
选取βij的演化方程为Prager形式:
| $ {\rm{d}}{\mathit{\boldsymbol{\beta }}_{ij}} = {c_1} \cdot {\rm{d}}\mathit{\boldsymbol{\varepsilon }}_{ij}^{p\left( 1 \right)}, $ | (9) |
式中:c1为常量参数,dεijp(1)为εijp(1)的微分.借鉴关联流动法则的公式,对其形式略加修改,取
| $ {\rm{d}}\mathit{\boldsymbol{\varepsilon }}_{ij}^{p\left( 1 \right)} = \mathit{\boldsymbol{n}}_{ij}^{\left( 1 \right)}{\rm{d}}{\lambda _1}, $ | (10) |
式中dλ1为比例因子 (非负标量).
边界面理论要求,屈服面只能在边界面之内或与边界面相切,绝不容许有任何部分超出边界面.在考虑这一约束条件下构造uij(1)的演化方程,其形式为
| $ {\rm{d}}\mathit{\boldsymbol{u}}_{ij}^{\left( 1 \right)} = - h \cdot \mathit{\boldsymbol{u}}_{ij}^{\left( 1 \right)}{\rm{d}}{\lambda _1}, $ | (11) |
其中h为A与A之间距离的函数:
| $ h = \frac{{{h_1}}}{{1 + {h_2}{{\left[ {{{\hat u}_0}/\left( {2R} \right)} \right]}^{{h_3}}}}} \cdot \frac{1}{{{{\hat u}_0} - \hat u + \delta }}, $ | (12) |
| $ \hat u = \sqrt {\mathit{\boldsymbol{u}}_{ij}^{\left( 1 \right)}\mathit{\boldsymbol{u}}_{ij}^{\left( 1 \right)}} . $ | (13) |
式中:h1、h2、h3为常量参数;û为当前应力点与边界面上映射点之间的有效距离;û0为当前应力点由弹性区域向着边界面移动过程中刚到达屈服面时对应的û值;δ为一个小正数,用来避免分母为零,其单位与应力的相同.对于本文的所有算例,当δ在[10-16, 0.5]内取值试算时,计算结果几乎相同,以滞回环卸载点应变εmax(即一次应力循环中的最大轴向应变) 为例,其变化范围的相对值小于1%.
对式 (6b) 等号两边取微分,再把式 (7)、(8) 带入其中,整理得
| $ {\rm{d}}\mathit{\boldsymbol{\alpha }}_{ij}^{\left( 1 \right)} = {\rm{d}}{\mathit{\boldsymbol{\beta }}_{ij}} + \left( {R - {r_1}} \right){\rm{d}}\mathit{\boldsymbol{n}}_{ij}^{\left( 1 \right)} - {\rm{d}}\mathit{\boldsymbol{u}}_{ij}^{\left( 1 \right)}, $ | (14) |
式中nij(1)是屈服面上当前应力点处法线单位向量,存在以下关系
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{n}}_{ij}^{\left( 1 \right)} = \left( {{\mathit{\boldsymbol{s}}_{ij}} - \mathit{\boldsymbol{\alpha }}_{ij}^{\left( 1 \right)}} \right)/\sqrt {\left( {{\mathit{\boldsymbol{s}}_{ij}} - \mathit{\boldsymbol{\alpha }}_{ij}^{\left( 1 \right)}} \right)\left( {{\mathit{\boldsymbol{s}}_{ij}} - \mathit{\boldsymbol{\alpha }}_{ij}^{\left( 1 \right)}} \right)} = }\\ {\left( {{\mathit{\boldsymbol{s}}_{ij}} - \mathit{\boldsymbol{\alpha }}_{ij}^{\left( 1 \right)}} \right)/{r_1},} \end{array} $ | (15) |
对上式求微分,并考虑式 (7),有
| $ {\rm{d}}\mathit{\boldsymbol{n}}_{ij}^{\left( 1 \right)} = \left( {{\rm{d}}{\mathit{\boldsymbol{s}}_{ij}} - {\rm{d}}\mathit{\boldsymbol{\alpha }}_{ij}^{\left( 1 \right)}} \right)/{r_1}. $ | (16) |
把式 (9)、(11)、(16) 带入式 (14),得
| $ {\rm{d}}\mathit{\boldsymbol{\alpha }}_{ij}^{\left( 1 \right)}{\rm{ = }}\left[ {{r_1}\left( {{c_1}\mathit{\boldsymbol{n}}_{ij}^{\left( 1 \right)} + h\mathit{\boldsymbol{u}}_{ij}^{\left( 1 \right)}} \right){\rm{d}}{\lambda _1} + \left( {R - {r_1}} \right){\rm{d}}{\mathit{\boldsymbol{s}}_{ij}}} \right]/R. $ | (17) |
在整个塑性加载中,一致性条件成立,所以
| $ {\rm{d}}{f_1} = 0. $ | (18a) |
将式 (4) 进行微分,有
| $ 2\left( {{\mathit{\boldsymbol{s}}_i} - \mathit{\boldsymbol{\alpha }}_{ij}^{\left( 1 \right)}} \right){\rm{d}}{\mathit{\boldsymbol{s}}_{ij}} - 2\left( {{\mathit{\boldsymbol{s}}_{ij}} - \mathit{\boldsymbol{\alpha }}_{ij}^{\left( 1 \right)}} \right){\rm{d}}\mathit{\boldsymbol{\alpha }}_{ij}^{\left( 1 \right)} - 2{r_1}{\rm{d}}{r_1} = 0. $ | (18b) |
将式 (7)~(17) 带入式 (18b),可求得
| $ {\rm{d}}{\lambda _1} = \frac{{\left( {{\mathit{\boldsymbol{s}}_{ij}} - \mathit{\boldsymbol{\alpha }}_{ij}^{\left( 1 \right)}} \right){\rm{d}}{\mathit{\boldsymbol{s}}_{ij}}}}{{\left( {{\mathit{\boldsymbol{s}}_{ij}} - \mathit{\boldsymbol{\alpha }}_{ij}^{\left( 1 \right)}} \right)\left( {{c_1}\mathit{\boldsymbol{n}}_{ij}^{\left( 1 \right)} + h\mathit{\boldsymbol{u}}_{ij}^{\left( 1 \right)}} \right)}}. $ | (19) |
塑性变形2及其相关量的描述采用只有屈服面 (无边界面) 的模型形式.屈服面方程为f2=0,设屈服函数f2为
| $ {f_2} = \left( {{\mathit{\boldsymbol{s}}_{ij}} - \mathit{\boldsymbol{\alpha }}_{ij}^{\left( 2 \right)}} \right)\left( {{\mathit{\boldsymbol{s}}_{ij}} - \mathit{\boldsymbol{\alpha }}_{ij}^{\left( 2 \right)}} \right) - {\left( {{r_2}} \right)^2}. $ | (20) |
式中:sij为偏应力张量;αij(2)、r2分别为偏应力空间中屈服面的圆心和半径,二者都是内变量.取:
| $ {\rm{d}}\mathit{\boldsymbol{\alpha }}_{ij}^{\left( 2 \right)} = {c_2}{\rm{d}}\mathit{\boldsymbol{\varepsilon }}_{ij}^{p\left( 2 \right)}, $ | (21) |
| $ {\rm{d}}{\mathit{r}_2} = b\left( {a - {r_2}} \right){\rm{d}}q. $ | (22) |
其中dq为有效塑性应变增量,取
| $ {\rm{d}}q = {\left( {\frac{2}{3}{\rm{d}}\mathit{\boldsymbol{\varepsilon }}_{ij}^{p\left( 2 \right)} \cdot {\rm{d}}\mathit{\boldsymbol{\varepsilon }}_{ij}^{p\left( 2 \right)}} \right)^{1/2}}, $ | (23) |
式中:a、b、c2均为材料常数,a表示r2的饱和值,b为r2的变化率常量.dεijp(2)为εijp(2)的微分,取
| $ {\rm{d}}\mathit{\boldsymbol{\varepsilon }}_{ij}^{p\left( 2 \right)} = \mathit{\boldsymbol{n}}_{ij}^{\left( 2 \right)}{\rm{d}}{\lambda _2}, $ | (24) |
式中dλ2为比例因子 (非负标量),nij(2)是屈服面上当前应力点处法线的单位向量.
由一致性条件有df2=0,再将式 (21)~(24) 带入df2=0,就可求得比例因子dλ2为
| $ {\rm{d}}{\lambda _2} = \frac{{\left( {{\mathit{\boldsymbol{s}}_{ij}} - \mathit{\boldsymbol{\alpha }}_{ij}^{\left( 2 \right)}} \right){\rm{d}}{\mathit{\boldsymbol{s}}_{ij}}}}{{{r_2}\left[ {{c_2} + \sqrt {\frac{2}{3}} b\left( {a - {r_2}} \right)} \right]}}. $ | (25) |
为了对第k(k=1、2) 个塑性变形对应的加载、卸载进行判断,引入加载函数Lk:
| $ {L_k} = \frac{{\partial {f_k}}}{{\partial {\mathit{\boldsymbol{s}}_{ij}}}}{\rm{d}}{\mathit{\boldsymbol{s}}_{ij}}. $ | (26) |
1) 当fk < 0时,材料状态在弹性区域内,相应不可逆变化量的增量为零;
2) 当fk=0时,材料状态在屈服面上,进一步分为两种情况:Lk>0时,应力变化为加载,相应内变量的变化分别使用式 (7)~(19) 和 (21)~(25) 来计算;Lk≤0时,应力变化为卸载或中性变载,相应的内变量不发生变化.
把与屈服函数f1相关的加载准则分解为3种情况:① f1 < 0;② f1=0, L1>0;③ f1=0, L1≤0.再把与屈服函数f2相关的加载准则分解为3种情况:(a)f2 < 0;(b)f2=0, L2>0;(c)f2=0, L2≤0.二者组合有3种情况:1) 当同时满足② 和 (a) 时,仅f1参与塑性计算;2) 当同时满足① 和 (b) 时,仅f2参与塑性计算;3) 当同时满足② 和 (b) 时,两个屈服面都参与塑性计算.
1.4 边界面模型的修正文献[11-13]报道了对稳定材料施加非对称循环应力的实验.给出了通过实验得到的滞回环卸载点应变εmax与循环周次N之间的关系曲线,指出开始时应变随循环次数的增加而增加,但增加的速率
逐渐减慢,当棘轮应变达到一定值时,棘轮应变率将保持相对稳定.棘轮应变率的含义是dεmax/dN,即每增加一次荷载循环引起的滞回环中卸载点应变εmax的增加量.
为较准确描述棘轮率的变化,本文采用文献[11]中修正边界移动的方法,即:当等效塑性应变
本文模型引入参数p,当等效塑性应变值大于此参数时,边界面的随动中心保持不变.
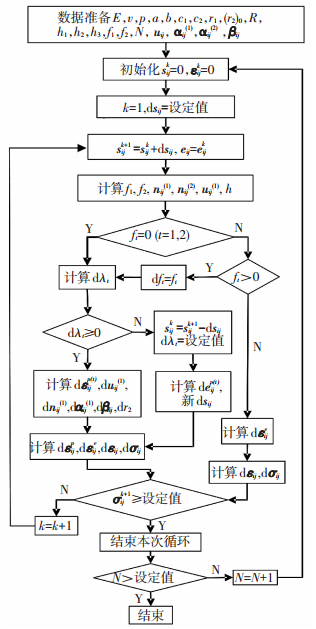
2 模型与实验结果比较采用文献[12]中材料U71Mn在单轴对称应变循环下和单轴非对称应力控制循环加载下的实验数据,对本文构建的模型进行验证.采用Compaq Visual Fortran6.6编写计算程序.以应力驱动给出所建本构模型的计算流程见图 2.
|
图 2 本构模型计算流程图 Figure 2 Calculation flow chart for the constitutive model |
记σxa和σxm分别为应力幅值和平均应力.模型参数的确定:材料U71Mn的弹性模量E和泊松比v采用文献[12]中的取值,其余材料参数借助棘轮行为的实验结果通过试算得到.本构模型中使用的材料参数见表 1, 其中 (r2)0为r2的初值,αij(1)、αij(2)、βij、εijp(1)和εijp(2)的初值均为0.
| 表 1 材料U71Mn的参数 Table 1 Parameters for U71Mn |
模拟以下几种单轴循环加载时材料U71Mn的力学行为:1) 循环荷载上下限为358±447 MPa (120周),见图 3;2) σxa恒定,分级变化σxm(各20周),见图 4;3) σxm恒定,分级增加σxa(各20周),见图 5;4) 平均应变为0,分级变化应变循环幅值,这时作用量是应变,响应量是应力,模拟的应力响应幅值σxa与循环周次N的关系见图 6.

|
图 3 U71Mn的单轴棘轮行为 (358±447 MPa) Figure 3 Uniaxial strain ratcheting of U71Mn under 358±447 MPa |
|
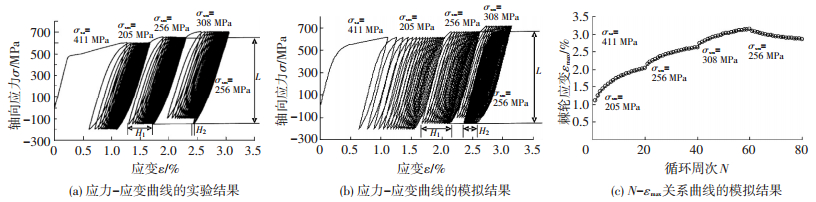
图 4 平均应力逐级变化时U71Mn的单轴棘轮行为 Figure 4 Uniaxial strain ratcheting of U71Mn with varying the mean stress in steps |
|
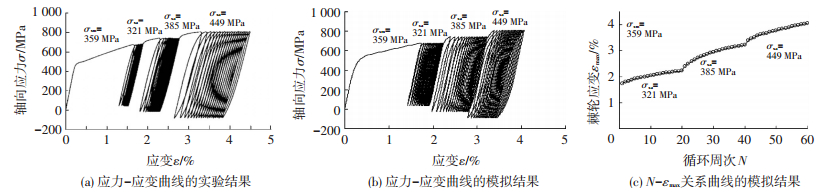
图 5 应力幅值逐级增加时U71Mn的单轴棘轮行为 Figure 5 Uniaxial strain ratcheting of U71Mn with increasing the stress cycle amplitude in steps |

|
图 6 应力响应幅值σxa与循环周次N的关系曲线的模拟结果与实验结果比较 (U71Mn材料,单轴应变对称循环加载) Figure 6 Comparison of stress amplitude-number of cycles curves between prediction and experiment (U71Mn under uniaxial symmetric strain cycling) |
图 3~5给出了材料U71Mn的轴向应力-应变曲线的模拟结果与实验结果的比较,以及εmax-N关系曲线的模拟结果.图 6给出了应力幅值-循环周次曲线的模拟结果与实验结果的比较.
从图 3~5可看出,U71Mn材料具有以下两个力学行为:1) 在循环初期,棘轮应变率随循环周次的增加而逐渐下降 (见图 3),达到一定的循环周次后,趋近于一个非零常值; 2) 在应力幅值为定值时,棘轮应变率随平均应力的增大而增大 (见图 4);在平均应力为定值时,棘轮应变率随应力幅值的增大而增大 (见图 5).本文模型能够模拟这两个性质.
在图 4中,L表示循环应力的幅值 (411 MPa);H1、H2分别为两段循环加载产生的塑性应变,这两段加载中平均应力、循环幅值及循环周数都相同.在这两段循环加载之间,材料经历了一段应力幅值和循环周数都与之相同、但平均应力更高的循环加载.从图 4可看出,H2 < H1,这说明一段平均应力更高的循环加载历史,使得之后的循环加载产生的塑性应变明显减少.观察图 4(b)~(c),本文模型能够模拟材料的这种行为特征.
从图 4、5可看出,本文模型在采用相同的参数时,即可对定平均值 (幅值变动) 或定幅值 (平均值变动) 循环荷载作用下的应力-应变曲线进行较好地模拟.克服了Tseng-Lee两面模型中模拟结果过度依赖参数的局限性.
从图 6可看出,该材料没有明显的最大应变幅值记忆效应,即在经历较大应变幅值循环之前和之后,两段上下限相同的应变循环加载产生的循环应力幅值基本相同.本文模型能够模拟材料的这种行为特征.
3 结论1) 在假设材料的不可逆行为是与时间、温度无关的条件下,基于边界面模型和多面模型理论,建立一个适用于描述金属稳定材料在循环加载情形下行为的三面本构模型.
2) 对边界面模型进行了改进,引入当前应力点与边界面上对偶点之间距离uij(1)的演变公式.该式的引入,提升了本构模型的模拟精度和适用范围.
3) 对室温下稳定材料U71Mn的单轴棘轮实验现象进行模拟,模拟曲线与实验曲线吻合较好,验证了模型的正确性和有效性.相比重在考虑由若干分项叠加的运动硬化准则的模型[12, 14-15],本文模型方程形式简单,参数较少,便于应用.
| [1] | JIANG Y, SEHITOGLU H. Comments on the Mroz multiple surface type plasticity models[J]. Int.J.Solids structures, 1996, 33(7): 1053-1068. DOI: 10.1016/0020-7683(95)00088-7 |
| [2] | HASHIGUCHI K. Mechanical requirements and structures of cyclic plasticity models[J]. International Journal of Plasticity, 1993, 9(6): 721-748. DOI: 10.1016/0749-6419(93)90035-0 |
| [3] | VOYIADJIS G Z, BASUROYCHOWDHURY I N. A plasticity model for multiaxial cyclic loading and ratcheting[J]. Acta Mechanica, 1998, 126(1/2/3/4): 19-35. DOI: 10.1007/BF01172796 |
| [4] | ITOH T, CHEN X, NAKAGAWA T, et al. A simple model for stable cyclic stress-strain relationship of type 304 stainless steel under nonproportional loading[J]. Journal of Engineering Materials and Technology, 2000, 122(1): 1-9. DOI: 10.1115/1.482758 |
| [5] | BARI S, HASSAN T. An advancement in cyclic plasticity modeling for multiaxial ratcheting simulation[J]. International Journal of Plasticity, 2002, 18(7): 873-894. DOI: 10.1016/S0749-6419(01)00012-2 |
| [6] | CHABOCHE J L. Modeling of ratchetting: evaluation of various approaches[J]. European journal of mechanics, 1994, 13(4): 501-518. |
| [7] | OHNO N, WANG J D. Kinematic hardening rules with critical state of dynamic recovery, part Ⅱ: application to experiments of ratcheting behavior[J]. International Journal of Plasticity, 1993, 9(3): 391-403. DOI: 10.1016/0749-6419(93)90043-P |
| [8] | MCDOWELL D L. Stress state dependence of cyclic ratcheting behavior of two rail steels[J]. International Journal of Plasticity, 1995, 11(4): 397-421. DOI: 10.1016/S0749-6419(95)00005-4 |
| [9] | CHABOCHE J L. On some modifications of kinematic hardening to improve the description of ratcheting effects[J]. International Journal of Plasticity, 1991, 7(7): 661-678. DOI: 10.1016/0749-6419(91)90050-9 |
| [10] | TSENG N T, LEE G C. Simple plasticity model of two-surface type[J]. Journal of Engineering Mechanics, 1983, 109(3): 795-810. DOI: 10.1061/(ASCE)0733-9399(1983)109:3(795) |
| [11] | HASSAN T.Ratcheting in cyclic plasticity of metals experiments and modeling [D].Austin: The University of Texas at Austin, 1993. |
| [12] |
康国政, 高庆. 循环稳定材料的棘轮行为: Ⅰ.实验和本构模型[J].
工程力学, 2005, 22(2): 206-211.
KANG Guozheng, GAO Qing. Ratcheting of cyclically stable material: Ⅰ.experiments and a visco-plastic constitutive model[J]. Engineering Mechanics, 2005, 22(2): 206-211. |
| [13] |
郭严, 康国政, 刘宇杰, 等. LZ50钢真应力控制下单轴棘轮行为的实验研究[J].
工程力学, 2010, 27(9): 216-220.
GUO Yan, KANG Guozheng, LIU Yujie, et al. Experimental study on uniaxial ratcheting of LZ50 steel under true stress-controlled cyclic loading[J]. Engineering Mechanics, 2010, 27(9): 216-220. |
| [14] | ABDEL-KARIM M. Modified kinematic hardening rules for simulations of ratcheting[J]. International Journal of Plasticity, 2009, 25(8): 1560-1587. DOI: 10.1016/j.ijplas.2008.10.004 |
| [15] | HAMIDINEJAD S M, VARVANI-FARAHANI A. Ratcheting assessment of steel samples under various non-proportional loading paths by means of kinematic hardening rules[J]. Materials and Design, 2015, 85: 367-376. DOI: 10.1016/j.matdes.2015.06.153 |
 2017, Vol. 49
2017, Vol. 49


