1984年,Shechtman等[1]首次在文献中报道了二十面体准晶后,准晶有别于传统晶体的特殊对称性引发了20世纪80年代和90年代准晶研究的热潮,Shechtman因对准晶研究的贡献于2011年获得了诺贝尔化学奖.在准晶的基础理论方面,我国从准晶被首次发现开始的很长一段时间内保持着国际领先地位[2],但在准晶的物理性能和工程应用方面, 和日本、法国等国相比仍存在一定差距.
根据对于准晶性能的文献报道,准晶具有低表面能[3]、低摩擦因数[4]、耐磨损[4-6]、优异的弥散强化特性[7]、高硬度[8]、高温塑性[9]、高热阻[10]、耐腐蚀[11]、高电阻[12]、储氢[13]等特点,同时块体准晶所表现出来的室温下高脆性[14]以及价格因素在一定程度上限制了准晶作为结构材料的商业化发展.目前, 准晶的应用在复合材料、表面涂层、块体准晶制备、储氢材料、光学材料等方面研究较多.如瑞典皇家工学院Nilsson等[15]研制的含准晶相析出的马氏体时效钢12%Cr-9%Ni-4%Mo-2%Cu-1%Ti,抗拉强度接近3 000 MPa,硬度可达730 HV.德州大学奥斯汀分校Lee等[16]研制的一种准晶相体积分数为71.18%的Al-Cu-Fe合金与碳化钨的平均摩擦因数为0.076,仅为相同条件下轴承钢的1/5,磨损率为1.41×10-5 mm3/(N·m), 为轴承钢的1/5.52.了解准晶的微观结构及机制,有助于更有针对性地研究其物理性能,开发其工程应用价值.
本文拟从准晶的发展历史、微观结构、近似相、研究现状和工程应用几方面介绍准晶体的研究进展与现状.
1 准晶体按对称性的分类根据准周期的维数,可以将准晶分为三维准晶、二维准晶、一维准晶.三维准晶分为二十面体对称准晶和立方准晶;二维准晶可分为十重准晶、八重准晶、十二重准晶、十八重准晶,下面对其作简要介绍.
1.1 三维准晶三维准晶多数为二十面体准晶,早期在急冷凝固的Al-Mn、Ti-Ni、Fe-Ti、Pd-U-Si等合金中观察到,后来随着稳定二十面体准晶在Al-Cu-Fe合金系中发现,又陆续在缓冷凝固的Al-Pd-TM、Mg-Zn-RE等合金系中发现稳定的二十面体准晶.二十面体准晶具有五重旋转对称、三重旋转对称和二重旋转对称,使其有别于五重孪晶而体现二十面体对称.根据结构,可分为简单二十面体准晶(Al-Mn(Al-Mn-Si)、Zn-Mg-Sc、Ti-Ni、Al-Li-Cu等)、面心二十面体(Al-Cu-Fe、Al-Pd-Mn、Al-Mg-Li、Zn-Mg-Re、Ho-Mg-Zn、Mg-Zn-Y-Zr等),体心二十面体虽然目前还没见报道,但已通过分子动力学模拟证明其存在的可能[17].根据准晶的团簇,目前已发现的二十面体准晶可分为:Mackay型准晶团簇、Bergman型准晶团簇、Tsai型准晶团簇. Mackay型准晶团簇可理解为两个互相嵌套的二十面体原子壳外再嵌套一层三十二面体(截顶二十面体)形成的团簇. Bergman型准晶团簇是第1层为二十面体原子壳,第2层为十二面体原子壳,第3层为二十面体原子壳互相嵌套形成的团簇. Tsai型准晶团簇为第1层四面体,第2层十二面体,第3层二十面体,第4层三十二面体互相嵌套而成.
此外,FENG等[18]发现了V-Ni-Si三维立方准晶,之后除了在快速凝固的Mg-Al合金中发现外,较少发现过类似准晶.目前的文献中对于三维准晶多数是指二十面体对称准晶,而对三维立方准晶考虑较少.
1.2 二维准晶二维准晶在一个平面上表现为准周期性,而在垂直于准周期平面的方向呈周期性排列.二维准晶可以根据二维准周期平面的旋转轴对称次数来分类,在实验中已发现八重准晶、十重准晶、十二重准晶及十八重准晶.
在二维准晶中,被发现次数最多的是十重准晶.最早发现的十重准晶是Bendersky等[19]在Al-Mn合金中发现的与二十面体准晶共生的十重对称准晶.同时KUO等[20]根据Mn-Ga十重准晶的电子衍射图指出,在三维二十面体准晶中,五重反轴间的夹角与十重对称准晶中十重轴与伪五重轴间的夹角角度相近,十重准晶与二十面体准晶存在可能的近亲关系. Schaefer等[21]首先在Al-Mn合金中观察到了二十面体准晶向十重准晶的转变,二十面体准晶的五重轴与十重准晶的十重轴和伪五重轴呈平行关系.其对应的准周期拼砌(彭罗斯拼砌)结构基元为36°菱形、72°菱形.目前为止,在Al-Mn、Al-Fe、Ga-Mn、Al-Cu-Co、Al-Co、Al-Pd-Mn、Al-Ni-Co、Al-Ir-Os等合金体系中发现十重准晶. Wasio等[22]在二茂铁甲酸在Au(1, 1, 1) 表面自组装试验中,发现除了少量二聚物和缺陷,扫描隧道显微镜下的图案显示,五聚体几乎覆盖了整个单分子层表面,即五重对称性. 图 1中用五边形表示出的区域与P1型的彭罗斯拼砌具有高度相似性.这是一种以弱氢键结合的有机十重对称准晶.

|
图 1 Au(1, 1, 1) 表面二茂铁甲酸的STM图与对应的P1型彭罗斯图[22] Figure 1 FcCOOH monolayer structure on Au(1, 1, 1) surface and corresponding P1 Penrose tiling[22] |
王宁等[23]首先在急冷Cr-Ni-Si及V-Ni-Si合金中发现二维八重准晶.八次准晶准周期面上对应的准周期拼砌图案由正方形和45°菱形两个结构基元组成.两种结构单元的准周期排列,构成八重准点阵,这些正方形、菱形的边都落在成45°的整数倍方向上,阵点排列呈准周期数列,相邻阵点间的距离之比的数列由1,
Ishimasa等[24]首先在急冷的Cr-Ni合金中发现二维十二重准晶.十二重准晶准周期面对应的准周期拼砌图案由3种结构基元组成:30°菱形、60°菱形、90°正方形,在其准周期拼砌中,每条边在30°的整数倍方向上.十二重对称准晶在Cr-Ni、V-Ni、V-Ni-Si、Ta-Te、Ta-V-Te等合金系中发现.同时,Zeng等[25]在超分子树枝状体系中观察到了十二重准晶,使得对原先准晶只存在于合金体系的认知拓展到了软物质准晶.
Fischer等[26]在研究PI30-PEO120胶团的相行为时的小角度X射线衍射发现,在质量分数为13%~18%,温度在15~20 ℃时,可以观察到十二重X射线衍射对称的稳定相,当温度在10 ℃时,可以观察到十八重X射线衍射对称的稳定相,即十八重准晶.
Dotera等[27]通过Monte Carlo法,模拟得到了二十四重准晶,但目前为止还未在实验中观测到.
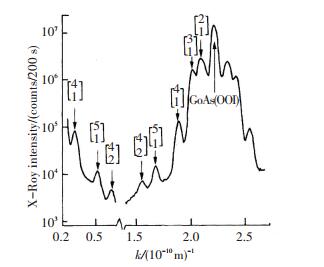
1.3 一维准晶类似于二维十重准晶与三维二十面体准晶存在的近亲关系,一维准晶常与二维十重准晶共生,其中一维准晶是由二维十重准晶中的一个与十重轴正交的二重准周期轴变成二重周期轴而生成的[28].一维准晶存在一个周期平面(两个正交的方向,一个是原来十重准晶的周期方向,另一个是十重准晶的十重轴变来的)和与周期平面垂直的准周期方向,这种准周期方向上的排列与Fibonacci数列有关.一维准晶自从1985年在GaAs-AlAs合金系中被发现[29]以来(见图 2),此后,在Mo-V、Ga-As-Al、Nb-Cu、Si-N、Al-Pd、Al-Cu-Ni、Al-Ni-Al、Al-Cu-Co等合金系中被发现[30].
此外,除了上述在实验条件下得到的准晶,2009年,Bindi等[31]在陨石中发现了天然准晶,这是人类第一次在实验室之外发现准晶,再一次拓展了人类关于准晶和天然矿物的认知,该准晶相为面心二十面体Al63Cu24Fe13准晶.这也促使大家思考准晶在自然条件下的形成机制,也为实验室在之前未涉及的温度和压强下研究新的准晶的形成和稳定性提供了思路. 2015年,该课题组在同一块陨石中又观察到了十重对称二维准晶,Al71Ni24Fe5准晶[32],该种准晶相在1 120~1 200 K的温度保持稳定,目前认为该准晶在45亿年前太阳系形成初期生成,当时在均匀的(1 100 K<T≤1 500 K)的温度下和5 GPa的大气压下发生碰撞并迅速降温[33].同时该陨石也体现了二十面体准晶与十重准晶存在的近亲关系.
2 准晶体相关的准周期模型构建方法尽管以前在金属玻璃中观察到的Frank-Kasper相也可以呈现二十面体对称[34-35],但Frank-Kasper相具有的有限范围的二十面体对称和较低的缺陷密度特点与实验中观察到的较高的向错密度和长程取向序有着较大区别,因此Levine等[36]排除了Frank-Kasper相的可能性,提出彭罗斯模型.尽管真实的准晶可能并非严格意义上的彭罗斯拼图,但准周期模型有助于进一步理解准晶的原子结构.
准晶体的结构模型有彭罗斯模型[36-39]、玻璃模型[40]、无规则堆砌模型[41]等.目前,讨论最多、影响最大的是彭罗斯模型,本文着重介绍彭罗斯模型.
根据已有的研究结果,在彭罗斯模型的构造中,介绍比较多的方法有:匹配与紧缩法,高维空间投影法和广义对偶法, 每一种方法所产生的准周期图案的种类不尽相同.
2.1 匹配与膨胀法准周期图具备高度的自相似性,并遵守一定的拼砌规则,这对得到新的准周期图有很大帮助.
对于一维准晶,相邻原子间的间距由L=τ=(1+
| $ \left[ {\begin{array}{*{20}{c}} {L'}\\ {S'} \end{array}} \right] \to \left[ {\begin{array}{*{20}{c}} 1&1\\ 1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} L\\ S \end{array}} \right]. $ |
这就是常说的Fibonacci数列.
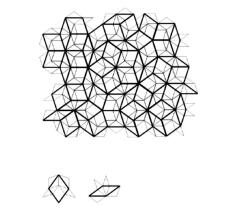
二维的彭罗斯图具有高度的自相似性,如图 3所示.
|
图 3 紧缩法则前后的彭罗斯单元的相互关系 Figure 3 Penrose tilings before and after deflation |
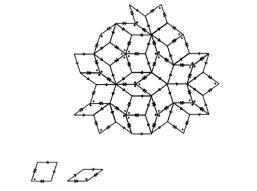
图中用粗线标示出两种菱形单元, 用这两种菱形按比例缩小成两种较小菱形装饰,边长缩小为原来的1/τ[42],经过紧缩法则变换后的两种较小菱形单元变成另一种彭罗斯图.准周期图案的匹配规则较为多样,如图 4所示.然而,符合匹配与紧缩法则的准周期拼砌在平铺的过程中并不是完全理想的,会产生少数缺陷.
|
图 4 彭罗斯拼砌的一种匹配法则 Figure 4 One kind of matching rules of Penrose tiling |
准周期拼砌也可通过多重网格的对偶得到,通过构建垂直于星坐标的N重网格,用ki表示该坐标在第i重网格中位于第ki条和ki+1条网格线之间,同理,N重网格中的某一封闭空间可以用[k1, …, kN]表示,则在与之对偶的空间中,该封闭空间对应于坐标为
通过广义对偶法所能产生的准周期模型种类最多,然而,在二维和三维情况下,多重网格中常常会存在奇异点,这时,需要作一些特殊处理,一定程度上增加了操作的复杂程度.
2.3 直接投影法准周期拼砌可看作高维空间向低维空间的投影,可以从高维空间中的超立方点阵通过垂直子空间窗口向平行子空间投影得到.
一维准晶的直接投影法相对于二维准晶和三维准晶的直接投影法更为直观,通过将二维网格中的条带范围内的点投影到所选取的投影线上得到[44].
图 5中,用实心圆标示出的空心圆在投影线上的投影的坐标为[38]
| $ {x_N} = N\hat a\cos \theta + \hat b\sin \left\lfloor {N\frac{{\hat a}}{{\hat b}}\tan \theta + \frac{{{y_0}}}{{\hat b}}} \right\rfloor . $ | (1) |
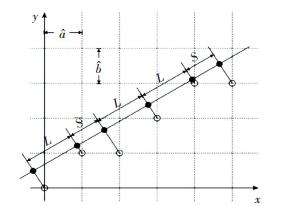
|
图 5 一维准晶的直接投影示意图 Figure 5 Schematic of direct projection method of one dimensional quasicrystal |
像一维准晶的直接投影法,准周期模型由高维空间En1+n2中的超立方点阵通过垂直子空间E⊥n2向平行子空间E‖n2投影所得[44-48].建立星坐标基矢集
| $ \begin{array}{l} {\left( {x_{\left\| {} \right.}^1, \ldots ,x_{\left\| {} \right.}^{{n_1}},x_ \bot ^{{n_1} + 1}, \ldots ,x_ \bot ^{{n_1} + {n_2}}} \right)^{\rm{T}}} = \\ \;\;\left( {{\boldsymbol{Q}^{\left\| {} \right.}},{\boldsymbol{Q}^ \bot }} \right){\left( {{n_1}, \ldots ,{n_{{n_1}}},{n_{{n_1} + 1}}, \ldots ,{n_{{n_1} + {n_2}}}} \right)^{\rm{T}}}. \end{array} $ |
相比于其他几种方法,直接投影法具有方便生成、容易定量描述的优点,便于建立与近似相的关系,计算衍射图案方面具有较大的优势,但能生成的准周期图案种类较为有限.
在准晶的有关文献中[49-51],也经常会用到Tubingen三角形,其实质和彭罗斯拼砌相同,且更便于操作.
3 准晶体的近似相实验发现,准晶经常与具有相似元素配比的近似相共生,准晶的近似相为晶体.基于二十面体Al-Mn-Si准晶与α-(Al-Mn-Si)晶体的相似性,Elser等[52]指出,准晶可以用周期为足够大的晶体近似.鉴于准晶的结构解析在实验上存在诸多困难,不同元素原子的位置难以确定,通过对于准晶体近似相晶体的研究有助于了解准晶的结构模型.准晶的近似相也可以通过高维空间投影得到.目前,除了Takakura等[53]和Tsai等[54]在解析出来的Cd-Yd准晶是结构清楚的准晶,其余均是通过与近似相结构有关的假设得到的.
当对高维空间进行切割时得到了准周期点阵,倘若在切割过程中,用一系列的连分数p/q(1/2 3/2 5/3…)去逼近黄金分割数τ,则得到的就是准晶的近似相,且随着连分数次数的增加,近似相的周期增大,与准晶之间拟合的程度也越好.
4 准晶性能的研究方法 4.1 实验研究对于准晶固有性能的研究,首先需要制备高质量的大块单准晶,制备过程中需要满足充足的缓冷凝固以及退火,使得准晶体生长过程中相位子弛豫,目前制备的工艺主要有Czochralski法、Bridgman法、自助溶剂法和浮区法. Czochralski法通过控制提拉速度、熔体温度以及籽晶杆的冷却速率制备块体准晶,并在块体d-Al-Co-Ni单准晶及其近似相单晶的制备中得到应用[55-56]; Bridgman法通过控制温度梯度以及生长速度使熔体在下拉过程中先在坩埚尖端形核并定向生长,被用来制备大块i-Ag-In-Yb单准晶,然而由于包晶反应和i-Ag-In-Yb与近似相液相线温度较为接近, 无法被用来制备其近似相[57]; 自助溶剂法依赖于熔体的元素配比以及倾析温度,当熔体通过液相线生长出近似相单晶体或单准晶还没产生其它相时将单准晶或近似相单晶与熔体分离,制备了大块i-Ag-In-Yb单准晶及其1/1、2/1近似相单晶和1/1Ag-In-Eu近似相单晶[58-59]; 浮区法控制铸锭与红外炉之间的相对运动,使得运动过程中铸锭的局部被不断融化,并随着籽晶沿着固定方向结晶,已被用于大块d-Al-Co-Ni单准晶和i-Al-Pd-Mn单准晶的制备[60-61].
通常认为由于准晶中位错的运动会产生相位子场层错,进而阻碍位错的运动[62]. Wollgarten等[63]对Al70Pd21Mn9在750 ℃下进行压缩变形实验,当变形量为25%时,位错密度比实验前增加了两个数量级,Mompiou等[64]指出,此时位错攀移占主导地位. Messerschmidt等[65]通过对比Al-Pd-Mn准晶的实验数据和理论分析,指出Al-Pd-Mn二十面体准晶中的Mackay型团簇在位错移动过程中扮演了障碍物的角色,此时位错的移动需要依靠热激活来实现. Texier等[66]在室温高压力(5 GPa)下观察到了Al66.27Pd21.88Mn11.85位错滑移的特征. Zou等[67]通过将Al70Pd21.5Mn8.5二十面体准晶加工成直径为150 nm~2 μm的一系列微柱,用压头进行压缩实验,在塑性变形过程中观察到了位错的滑移,同时,随着尺度的减小(510~350 nm),准晶的行为由脆性向韧性转变; 在100~500 nm,屈服强度维持在约4.5 GPa的较高值.在目前对于其他材料的微柱实验中,目前仅有测试的两种准晶Al70Pd21.5Mn8.5[67]二十面体准晶和Al77Ni10.5Co12.5[68]二维十重准晶相比都表现了极高的比强度(在1 MJ/kg左右). Schall等[69]在800 ℃~890 ℃温度下在二维十重准晶Al73Ni10Co17分别平行于、45°垂直于十重轴的方向进行压缩试验,垂直于十重轴方向的屈服强度四倍于45°方向的屈服强度,在不同方向上呈现出显著的塑性各向异性,Feuerbacher等[70]指出这可能与不同方向上的位错特征有关. Zou等[68]将对Al77Ni10.5Co12.5二维十重准晶微柱的3个方向进行压缩试验,发现随着微柱尺寸的减小,屈服强度和塑性的各向异性随之降低,直至几乎消失,并指出该现象与温度导致的位错阻力增加、尺寸缩小导致的位错更趋向与成核而非扩散,以及高应力和短的位错长度导致的多个滑移系开启等3个因素有关.实验中,在200~300 nm时,临界分剪切应力接近模拟值[49]. Laplanche等[71]对比了ω-Al7Cu2Fe晶体相与二十面体Al-Cu-Fe准晶,提出准晶与晶体具有相似的变形机制,认为在准晶位错的运动过程中,虽然需要考虑相位子场缺陷和团簇的作用,但并不主导位错的运动过程,这与先前的理论存在一定冲突,可作参考.
在准晶材料的表面性能方面,实验观察到了Al-Cu-Fe准晶具有低摩擦因数[4]及较高的硬度. Brunet等[7]比较了多种材料摩擦因数与硬度的关系,指出准晶的低摩擦因数不仅与其高硬度有关,也可能是由其较低的电子间相互作用造成的. Dubois等[3]通过Al-Cu-Fe准晶的润湿性实验,测得准晶表面与水的黏着能仅为特氟龙的1.25倍. Park等[72]通过原子力显微镜测试了Al-Ni-Co二维十重准晶不同方向上的摩擦性能,观察到了显著的各向异性,在周期方向的扭转力为准周期方向的8.2±0.44倍. Filippov等[73]提出的拓扑模型解释了准晶摩擦性能的各向异性,认为这是由于在两个方向上的原子平均间距不同导致的. Ye等[74]模拟了准晶的近似相与原子力显微镜尖端的接触,模拟出的数值与实验相差较大,提出了准晶的各向异性可能由尖端钝化的硫醇与准晶在周期方向的沟纹的卷吸作用引起的黏着摩擦造成的. Dubois等[75]对Al-Mn-Pd与两种航空材料SS316L和AlSi52100进行微动磨损实验(5 N法向载荷,100次振动)后测量黏着力,几乎未发生黏着.根据以往对于晶体摩擦性能的研究,可以将摩擦因数分为黏着项和犁沟项[76].而犁沟项与晶体的硬化[77-78]、高温下的热激活[79]、再结晶[80-81]以及磨粒的剪切有关; 黏着项与晶体的表面能[82]、晶面上的临界分切应力[82]等因素有关.类似地,对准晶塑性变形的深入研究有助于进一步探索其摩擦性能.
准晶的表面结构与其表面性能有关,将离子溅射后进行退火处理的准晶表面在高真空环境下使用扫瞄隧道显微镜和低能电子衍射分析其表面结构.对于Al-Pd-Mn和Al-Cu-Fe二十面体准晶的五重表面,材料表面出现了一系列平台,平台之间的高度为L和S两种比值为黄金数的距离的线性组合,排列符合Fibonacci数列.表层为原子密排面,表层中Al元素含量较高,有利于降低表面能.在Al-Cu-Fe二十面体准晶的五重表面上还观察到了五边形浅坑和螺型位错[83-85].在Al-Pd-Mn二十面体准晶三重表面的平台上,呈现小面生长的趋势[86],其二重表面平台之间的高度符合Fibonacci数列并出现小面生长[87],表明Al-Pd-Mn准晶二重和三重表面的稳定性弱于五重表面.对于Al-Pd-Re多晶准晶的实验分析结果表明,其二重表面相比于其他两种表面更稳定[88]. Ag-In-Yb准晶的表面分析结果表明:其3种对称表面都穿过菱形三十面体团簇中心,仅有二重表面是对应方向上原子密度最高的面,3种对称表面都是对应方向上Ag原子含量较低的面,使其具有相对较低的表面能; 在3种表面上都没有观察到小面生长,表明这3个面都是稳定的面,起连接作用的Yb原子相比于团簇中的Yb原子更不稳定,会降低平台表面的稳定性[89-91]. Al-Co-Ni十重准晶在二重表面上的原子结构在十重轴方向上周期性排布,在二重轴方向上的排布呈现Fibonacci数列,与Takakura等提出的模型较符合[92-93].准晶的清洁表面也被用来作为模板制备新型薄膜. Ledieu等[94]将铜原子沉积在i-Al-Pd-Mn的五重表面,铜原子分别在五重表面的5个主方向上形成条带,在主方向上原子呈周期性排列,在垂直于主方向上呈符合Fibonacci数列的准周期性排列,在580 K退火后准周期性消失. Ledieu等[95]将Si原子沉积在i-Al-Pd-Mn的五重表面,观察到Si原子被吸附在伪Mackay型团簇的中心位置,并认为与Mn原子周围价电荷密度最大,与Si原子形成共价键有关[96]. Pd原子在i-Al-Pd-Mn准晶五重表面的单层原子沉积表面,Pd原子在基体上出现准周期排列,与基体的常数之比为黄金数1.618,并在费米能级上呈现赝能隙[97]. Yadav等[30]将i-Al-Cu-Fe准晶表面用NaOH溶液化学浸出后,通过扫描电子显微镜观察其表面,结果显示i-Al-Cu-Fe准晶表面出现了大量尺寸规则的纳米Cu立方体和少量的纳米Fe立方体,为纳米结构材料的合成提供了新思路.
在准晶体的磁学、电学以及热电性质等方面,对于d-Al-Co-Ni及d-Al-Cu-Co的研究表明,300 K时垂直和平行于十重轴方向上的电阻率之比分别为8和7,且在垂直于十重轴方向上呈现负的温度系数,在平行于十重轴方向上呈现正的温度系数[98].实验测得近似相Y-Al-Ni-Co在赝准周期平面内的两个方向上表现为相差不大的正的磁化系数,而赝十重轴方向上表现为负的磁化系数且绝对值比赝准周期平面内大很多[99]. d-Al-Co-Ni的塞贝克系数在十重轴方向上呈现先下降后上升的趋势, 并由负值变为正值,在准周期平面内各方向上相近,十重轴方向与准周期平面内的塞贝克系数差别较大[100].需要引起特别注意的是,不同文献中即使对于同种准晶相同物理量的测量在数值或趋势上也有较大差异,可能与样品品质及氧化层有关[101]. Bobnar等[100, 102]分析了十重准晶对称性与张量的关系,认为理想的十重准晶在准周期平面内为各向同性,准周期平面内与十重轴之间各向异性,并比较了d-Al-Co-Ni不同方向上的磁化系数、电阻率、霍尔系数、摩尔比热、导热系数,验证了这一观点.通过分析二十面体对称性与张量的关系,理想的二十面体对称结构的物理性能应为各项同性,与i-Ag-In-Yb准晶的磁化系数、电阻率、霍尔系数、摩尔比热、导热系数在二重轴、三重轴、五重轴上相近的实验数据吻合.
4.2 模拟方法目前,除了实验手段,随着计算机科学的发展,对于准晶力学与机械性能模拟的手段趋于多样化,主要有连续介质力学方法[103],分子动力学模拟方法[49-51, 74, 104-113],有限元方法[114-116]等.
连续介质力学方法在现有的准晶力学行为的研究上应用最多,研究范围最广,以国内范天佑[104]等学者为代表,将具体问题转化成偏微分方程边界值问题,得到应力场的解析解.
如果在原子尺度上研究准晶塑性及断裂行为的微观机理,分子动力学模拟是一条直观且有效的途径. Mikulla等[49-51]模拟了二维十次准晶在变形过程中的位错运动,观察到了准晶中位错运动时, 其后会伴随着相位子场层错,指出其脆性与相位子场层错存在关系; 而准晶中的团簇对位错和裂纹尖端的移动起到阻碍的作用,当第一条位错切过团簇体时会减弱该团簇的阻碍作用,造成应变软化,提出位错发射-相位子墙-断裂机制. Trebin等[105]模拟了二元平面准晶的裂纹扩展,指出二元二维准晶发生I型裂纹的过程中,位错尖端向36°方向发射位错,并在其后产生相位子场层错,沿着层错方向材料强度降低,材料容易开裂,且相位子场层错处键能下降,更容易生成位错,造成软化. Bunz等[104]基于原子跳跃引起了相位子场缺陷,模拟了十重对称Al-Cu-Co中的原子跳跃,指出Al原子比过渡金属更易动,跳跃方向倾向于沿着十重对称轴方向或准周期平面上. Schaaf等[106]模拟了三维二十面体准晶在两种剪切变形下的刃型位错运动,观测到了伴有位错攀移的位错滑移,并在位错运动过程中某些特定点上产生了钉扎效应,使得位错线呈弯曲状,并指出稳定的团簇可能是准晶位错控速机制中的重要因素,位错更倾向于在垂直于二重轴的平面上运动. Rudhart等[109]模拟了在不同温度下二维二元准晶的断裂,指出准晶在3种不同温度区间内的3种不同失效模式. ENGEL等[113]模拟了准晶相位子场翻转,指出势能比均值更高的粒子更容易发生相位子场翻转.尽管分子动力学模拟方法直观有效,但是目前为止,在大多数模拟中所采用的原子模型和势函数都采取了比较理想化的人为简化,模拟结果虽然在一定程度上能反映准晶的某些特性,但其精确性仍然有待提高.由于准晶体系中原子几何排列的复杂性,与晶体的势函数选取不同的是,准晶中的势函数通常具有若干个能量极值点,也就是需要引入振荡项.在模拟过程中的势函数,最早采用的是L-J势,之后的文献中有采用了EAM势,以及精度相对较高的基于第一性原理计算得到的Realistic型对势.早期的准晶建模较多依赖于Tubingen三角形,而目前主要采取其近似相模型.随着Yb-Cd准晶的成功解析[53], 近年来又成功解析了Sc-Zn准晶[117],为Tsai型二元准晶原子结构的精修提供了基础[118],从而为之后准晶的精确模拟提供了便利.
在较为复杂的工程应用中,有限元方法提供了获得数值解的新思路.杨连枝等[114]提出通过立方准晶广义能量泛函的变分方法得到静力问题的有限元解法,并模拟了受到拉伸载荷的含有圆片状裂纹的圆柱,其模拟结果与解析解结果较为一致.尽管提出准晶体的有限元模拟较晚,但随着准晶体的工程化应用,有限元模拟对于准晶在复杂工程问题上的数值求解有明显优势.
5 应用前景表面涂层材料.考虑到准晶体材料具有低粘着性,并且相对于传统不粘锅材料特氟龙具有耐刮擦、高温稳定的特点,基于准晶体的不粘锅已有专利.准晶体较低的表面润湿性以及高硬度造成了其较强的耐磨性以及较低的摩擦因数,使得其成为一种潜在的减摩涂层材料;但是表面氧化膜增加了其脆性,在工程应用中需要克服其表面氧化膜带来的不利影响. AlCuFe等准晶具有与传统隔热涂层材料ZrO2类似的导热系数,与ZrO2不同的是,准晶涂层与金属基体具有相似的体积膨胀系数,减小了涂层与基体之间的应力,但受到了铝基合金熔点普遍不高的限制,可使用温度不如ZrO2,无法用于大型客机,但比较适合用于小型发动机叶片.
复合材料增强相.块体准晶呈现较为普遍的高脆性以及体积的限制使其目前难以作为结构材料,但将其作为弥散增强相,仍可以保持较高的强度,可显著增加其韧性,并具有较低的摩擦因数和磨损率.前文中提到的含准晶相析出的马氏体时效刚12%Cr-9%Ni-4%Mo-2%Cu-1%Ti就是一个较为成功的应用. Kenzari等[119]通过3D计算机辅助技术用选择性激光烧结的方法得到的含AlCuFeB的聚酰胺零部件已得到应用,该聚合物复合材料与其基体材料相比,摩擦因数和磨损率分别为后者的63%和30%,表面性能显著提高.
此外,准晶体在储氢材料、催化剂和光学材料方面也具有应用价值.
6 存在的问题目前, 准晶性能与工程应用仍存在如下需要进一步研究的问题:
1) 对于准晶结构的认知仍较为有限,应利用已有的结构分析方法以及准晶近似相的分析结果,对准晶模型进行结构精修.
2) 用于模拟准晶的势函数以具有多个能量极值点为特征,精度高于传统势函数,需要通过第一性原理计算得到.
3) 利用分子动力学模拟等方法,对准晶的结构以及动力学行为进行探索,为新型准晶的发现和设计提供思路.
4) 进行准晶的微观模拟研究,在原子尺度上分析准晶的塑性变形机制以及材料缺陷的演化.
5) 准晶材料的改性研究问题.准晶仍受到高脆性的制约,需要寻找新的同时具有高韧性和高强度的合金系.
6) 准晶材料的成本控制问题, 尽管随着工艺提高,准晶的制造成本已显著下降,块材成品体积与品质提升,但与传统金属材料相比仍不具备明显优势.
7) 准晶的机械及力学行为的研究,建立动态断裂以及摩擦学模型,以便于更好地利用准晶.
8) 准晶材料机械零件的开发,例如准晶材料滚动轴承和齿轮涂层的研究.
9) 准晶机械零件的设计准则与设计方法的研究.利用准晶材料的特殊性能,用于机械产品设计.
7 结束语目前,准晶及其近似相的性能研究仍受到块体体积与品质的限制,高质量大块单准晶及近似相单晶制备工艺的优化有利于准晶性能的更深入研究.当前已发现的准晶所呈现的高脆性限制了其作为结构材料的应用,可利用准晶弥散强化,低摩擦系数的特点开发适用于具体工况的低成本表面涂层和复合材料.在理论研究方面,其模拟精度仍然受到其结构模型和原子间相互作用势的制约.准晶原子结构的解析仍然有待发展,其有助于计算模拟精度的提高,为准晶及含准晶相合金的物理机制的研究和进一步工程化应用提供基础.
| [1] | SHECHTMAN D, BLECH I, GRATIAS D, et al. Metallic phase with long-range orientational order and no translational symmetry[J]. Physical Review Letters, 1984, 53(20): 1951-1953. DOI: 10.1103/PhysRevLett.53.1951 |
| [2] | ZHANG Z, YE H Q, KUO K H. A new icosahedral phase with m35 symmetry[J]. Philosophical Magazine A, 1985, 52(6): L49-L52. DOI: 10.1080/01418618508242135 |
| [3] | DUBOIS J M. New prospects from potential applications of quasicrystalline materials[J]. Materials Science and Engineering: A, 2000, 294: 4-9. DOI: 10.1016/S0921-5093(00)01305-8 |
| [4] | RABSON D A. Toward theories of friction and adhesion on quasicrystals[J]. Progress in Surface Science, 2012, 87(9): 253-271. DOI: 10.1016/j.progsurf.2012.10.001 |
| [5] | OLSSON S, BROITMAN E, GARBRECHT M, et al. Mechanical and tribological properties of AlCuFe quasicrystal and Al(Si)CuFe approximant thin films[J]. Journal of Materials Research, 2016, 31(2): 232-240. DOI: 10.1557/jmr.2015.384 |
| [6] | BRUNET P, ZHANG L M, SORDELET D J, et al. Comparative study of microstructural and tribological properties of sintered, bulk icosahedral samples[J]. Materials Science and Engineering: A, 2000, 294: 74-78. DOI: 10.1016/S0921-5093(00)01202-8 |
| [7] | INOUE A, ZHANG Tao, CHEN Minwei, et al. Mechanical properties of bulk amorphous Zr-Al-Cu-Ni-Ag alloys containing nanoscale quasicrystalline particles[J]. Materials Transactions, 1999, 40(12): 1382-1389. DOI: 10.2320/matertrans1989.40.1382 |
| [8] | WITTMANN R, URBAN K, SCHANDL M, et al. Mecanical properties of single quasicrystalline AlCuCoSi[J]. Journal of Materials Research, 1991, 6(6): 1165-1168. DOI: 10.1557/JMR.1991.1165 |
| [9] | YOKOYAMA Y, INOUE A, MASUMOTO T. Mechanical-properties, fracture mode and deformation-behavior of Al70Pd20Mn10 single quasicrystal[J]. Materials Transactions Jim, 1993, 34(2): 135-145. DOI: 10.2320/matertrans1989.34.135 |
| [10] | BLAS F J G, ALGABA J M, ALVAREZ J, et al. Application of quasicrystalline materials as thermal barriers in aeronautics and future perspectives of use for these materials[C] // MRS 1998 Fall Meeting. [S.l.]: Cambridge Univ Press, 1998:447.DOI: 10.1557/PROC-553-447. |
| [11] | DUBOIS J M, KANG S S, MASSIANI Y. Application of quasicrystalline alloys to surface coating of soft metals[J]. Journal of Non-Crystalline Solids, 1993, 153: 443-445. DOI: 10.1016/0022-3093(93)90392-B |
| [12] | MIGLIERINI M, NASU S. Magnetic, electronic and structure-pro-perties of icosahedral quasicrystals[J]. Materials Transactions Jim, 1993, 34(2): 178-187. DOI: 10.2320/matertrans1989.34.178 |
| [13] | STROUD R M, VIANO A M, GIBBONS P C, et al. Stable Ti based quasicrystal offers prospect for improved hydrogen storage[J]. Applied physics letters, 1996, 69(20): 2998-3000. DOI: 10.1063/1.117756 |
| [14] | LUBENSKY T C, RAMASWAMY S, TONER J. Dislocation motion in quasicrystals and implications for macroscopic properties[J]. Physical Review B, 1986, 33(11): 7715-7719. DOI: 10.1103/PhysRevB.33.7715 |
| [15] | LIU P, STIGENBERG A H, NILSSON J O. Quasicrystalline and crystalline precipitation during isothermal tempering in a 12Cr9Ni4Mo maraging stainless steel[J]. Acta Metallurgica Et Materialia, 1995, 43(7): 2881-2890. DOI: 10.1016/0956-7151(94)00461-P |
| [16] | LEE K, HSU J L, NAUGLE D, et al. Multi-phase quasicrystalline alloys for superior wear resistance[J]. Materials & Design, 2016, 108: 440-447. DOI: 10.1016/j.matdes.2016.06.113 |
| [17] | ENGEL M, DAMASCENO P F, PHILLIPS C L, et al. Computational self-assembly of a one-component icosahedral quasicrystal[J]. Nature Materials, 2015, 14(1): 109-116. DOI: 10.1038/nmat4152 |
| [18] | FENG Y C, LU G, WITHERS R L. An incommensurate structure with cubic point group symmetry in rapidly solidified V-Ni-Si alloy[J]. Journal of Physics Condensed Matter, 1989, 1(23): 3695-3700. DOI: 10.1088/0953-8984/1/23/015 |
| [19] | BENDERSKY L. Quasicrystal with one-dimensional translational sy-mmetry and a tenfold rotation axis[J]. Physical Review Letters, 1985, 55(14): 1461-1463. DOI: 10.1103/PhysRevLett.55.1461 |
| [20] | WU J S, KUO K H. Decagonal quasicrystal and related crystalline phases in Mn-Ga alloys with 52 to 63 a/o Ga[J]. Metallurgical and Materials Transactions A, 1997, 28(13): 729-742. DOI: 10.1007/s11661-997-1000-y |
| [21] | SCHAEFER R J, BENDERSKY L. Replacement of icosahedral AlMn by decagonal phase[J]. Scripta Metallurgica, 1986, 20(5): 745-750. DOI: 10.1016/0036-9748(86)90504-1 |
| [22] | WASIO N A, QUARDOKUS R C, FORREST R P, et al. Self-assembly of hydrogen-bonded two-dimensional quasicrystals[J]. Nature, 2014, 507(7490): 86-89. DOI: 10.1038/nature12993 |
| [23] | WANG N, CHEN H, KUO K H. Two-dimensional quasicrystal with eightfold rotational symmetry[J]. Physical Review Letters, 1987, 59(9): 1010-1013. DOI: 10.1103/PhysRevLett.59.1010 |
| [24] | ISHIMASA T, NISSEN H U, FUKANO Y. New ordered state between crystalline and amorphous in Ni-Cr particles[J]. Physical Review Letters, 1985, 55(55): 511-513. DOI: 10.1103/PhysRevLett.55.511 |
| [25] | ZENG Xiangbing, UNGAR G, LIU Yongsong, et al. Supramolecular dendritic liquid quasicrystals[J]. Nature, 2004, 428(6979): 157-160. DOI: 10.1038/nature02368 |
| [26] | FISCHER S, EXNER A, ZIELSKE K, et al. Colloidal quasicrystals with 12-fold and 18-fold diffraction symmetry[J]. Proceedings of the National Academy of Sciences, 2011, 108(5): 1810-1814. DOI: 10.1073/pnas.1008695108 |
| [27] | DOTERA T, OSHIRO T, ZIHERL P. Mosaic two-lengthscale quasicrystals[J]. Nature, 2014, 506(7487): 208-211. DOI: 10.1038/nature12938 |
| [28] |
周公度, 郭可信.
晶体和准晶体的衍射[M]. 北京: 北京大学出版社, 1999: 251-252.
ZHOU Gongdu, GUO Kexin. Diffraction of crystal and quasicrystal[M]. Beijing: Peking University Press, 1999: 251-252. |
| [29] | MERLIN R, BAJEMA K, CLARKE R, et al. Quasiperiodic gaas-alas heterostructures[J]. Physical Review Letters, 1985, 55(17): 1768-1770. DOI: 10.1103/PhysRevLett.55.1768 |
| [30] | YADAV T P, MISHRA S S, SRIVASTAVA O N. Copper nanocubes on Al 65 Cu 20 Fe 15 quasicrystalline surface[J]. Journal of Alloys and Compounds, 2017, 712: 134-138. DOI: 10.1016/j.jallcom.2017.04.058 |
| [31] | BINDI L, STEINHARDT P J, YAO Nan, et al. Natural quasicrystals[J]. science, 2009, 324(5932): 1306-1309. DOI: 10.1126/science.1170827 |
| [32] | BINDI L, YAO N, LIN C, et al. Natural quasicrystal with decagonal symmetry[J]. Scientific Reports, 2015(5): 9111. DOI: 10.1038/srep09111 |
| [33] | HOLLISTER L S, BINDI L, YAO N, et al. Impact-induced shock and the formation of natural quasicrystals in the early solar system[J]. Nature Communications, 2014(5): 4040. DOI: 10.1038/ncomms5040 |
| [34] | FRANK F C T, KASPER J S. Complex alloy structures regarded as sphere packings. Ⅱ. Analysis and classification of representative structures[J]. Acta Crystallographica, 1959, 12(7): 483-499. DOI: 10.1107/S0365110X59001499 |
| [35] | FRANK F C, KASPER J S. Complex alloy structures regarded as sphere packings. Ⅰ. Definitions and basic principles[J]. Acta Crystallographica, 1958, 11(3): 184-190. DOI: 10.1107/S0365110X58000487 |
| [36] | LEVINE D, STEINHARDT P J. Quasicrystals: a new class of ordered structures[J]. Physical Review Letters, 1984, 53(26): 2477-2480. DOI: 10.1103/PhysRevLett.53.2477 |
| [37] | LEVINE D, STEINHARDT P J. Quasicrystals. Ⅰ. Definition and structure[J]. Physical Review B, 1986, 34(2): 596-616. DOI: 10.1103/PhysRevB.34.596 |
| [38] | SOCOLAR J E S, STEINHARDT P J. Quasicrystals. Ⅱ. Unit-cell configurations[J]. Physical Review B, 1986, 34(2): 617-647. DOI: 10.1103/PhysRevB.34.617 |
| [39] | PENROSE R. Pentaplexity a class of non-periodic tilings of the plane[J]. Mathematical Intelligencer, 1979, 2(1): 32-37. DOI: 10.1007/BF03024384 |
| [40] | STEPHENS P W, GOLDMAN A I. The structure of quasicrystals[J]. Scientific American, 1991, 150-151(3/4): 44-47. DOI: 10.1038/scientificamerican0491-44 |
| [41] | WIDOM M, STRANDBURG K J, SWENDSEN R H. Quasicrystal equilibrium state[J]. Physical Review Letters, 1987, 58(7): 706-709. DOI: 10.1103/PhysRevLett.58.706 |
| [42] | BRUIJN N G. Algebraic theory of Penrose′s non-periodic tilings of the plane. Ⅱ[C] // Indagationes Mathematicae (Proceedings). North-Holland:Elsevier, 1981:53-66.DOI: 10.1016/1385-7258(81)90017-2. |
| [43] | SOCOLAR J E S, STEINHARDT P J, LEVINE D. Quasicrystals with arbitrary orientational symmetry[J]. Physical Review B, 1985, 32(8): 5547-5550. DOI: 10.1103/PhysRevB.32.5547 |
| [44] | ELSER V. Indexing problems in quasicrystal diffraction[J]. Physical Review B, 1985, 32(8): 4892-4898. DOI: 10.1103/PhysRevB.32.4892 |
| [45] | WANG Z M, KUO K H. The octagonal quasilattice and electron diffraction patterns of the octagonal phase[J]. Acta Crystallographica Section A: Foundations of Crystallography, 1988, 44(6): 857-863. DOI: 10.1107/S0108767388004921 |
| [46] | ISHIHARA K N, YAMAMOTO A. Penrose patterns and related structures. Ⅰ. Superstructure and generalized Penrose patterns[J]. Acta Crystallographica Section A: Foundations of Crystallography, 1988, 44(4): 508-516. DOI: 10.1107/S0108767388002958 |
| [47] | YAMAMOTO A, ISHIHARA K N. Penrose patterns and related structures. Ⅱ. Decagonal quasicrystals[J]. Acta Crystallographica Section A: Foundations of Crystallography, 1988, 44(5): 707-717. DOI: 10.1107/S010876738800296X |
| [48] | YANG Q B, WEI W D. Description of the dodecagonal quasicrystal by a projection method[J]. Physical Review Letters, 1987, 58(10): 1020-1023. DOI: 10.1103/PhysRevLett.58.1020 |
| [49] | MIKULLA R, ROTH J, TREBIN H R. Simulation of shear-stress in 2-dimensional decagonal quasicrystals[J]. Philosophical Magazine B-Physics of Condensed Matter Statistical Mechanics Electronic Optical and Magnetic Properties, 1995, 71(5): 981-989. DOI: 10.1080/01418639508243601 |
| [50] | MIKULLA R, GUMBSCH P, TREBIN H R. Dislocations in quasicrystals and their interaction with cluster-like obstacles[J]. Philosophical Magazine Letters, 1998, 78(5): 369-376. DOI: 10.1080/095008398177760 |
| [51] | MIKULLA R, STADLER J, KRUL F, et al. Crack propagation in quasicrystals[J]. Physical Review Letters, 1998, 81(15): 3163-3166. DOI: 10.1103/PhysRevLett.81.3163 |
| [52] | ELSER V, HENLEY C L. Crystal and quasicrystal structures in Al-Mn-Si alloys[J]. Physical review letters, 1985, 55(26): 2883-2886. DOI: 10.1103/PhysRevLett.55.2883 |
| [53] | TAKAKURA H, GÓMEZ C P, YAMAMOTO A, et al. Atomic structure of the binary icosahedral Yb-Cd quasicrystal[J]. Nature Material, 2007, 6(6): 58-63. DOI: 10.1038/nmat1799 |
| [54] | TSAI A P, GUO J Q, ABE E, et al. Alloys: A stable binary quasicrystal[J]. Nature, 2000, 408(6812): 537-538. DOI: 10.1038/35046202 |
| [55] | BAUER B, MEISTERERNST G, HAERTWIG J, et al. Czochralski growth and X-ray topographic characterization of decagonal AlCoNi quasicrystals[J]. Philosophical Magazine, 2006, 86(3/4/5): 317-322. DOI: 10.1080/14786430500253927 |
| [56] | GILLE P, BAUER B, HAHNE M, et al. Single crystal growth of Al-based intermetallic phases being approximants to quasicrystals[J]. Journal of Crystal Growth, 2011, 318(1): 1016-1020. DOI: 10.1016/j.jcrysgro.2010.10.021 |
| [57] | CUI C, TSAI A P. Growth of large single-grain quasicrystals in the Ag-In-Yb system by Bridgman method[J]. Journal of Crystal Growth, 2009, 312(1): 131-135. DOI: 10.1016/j.jcrysgro.2009.09.038 |
| [58] | CUI C, TSAI A P. Growth of large-grain Ag-In-Yb icosahedral quasicrystals and approximant crystals[J]. Journal of Alloys & Compounds, 2012, 536(5): 91-93. DOI: 10.1016/j.jallcom.2012.05.031 |
| [59] | CUI C, TSAI A P. Synthesis of large single-grain 1/1 approximant crystals in the Ag-In-Eu system by the self-flux method[J]. Philosophical Magazine, 2011, 91(19/20/21): 2443-2449. DOI: 10.1080/14786435.2010.511600 |
| [60] | SATO T J, HIRANO T, TSAI A P. Single-crystal growth of the decagonal Al-Ni-Co quasicrystal[J]. Journal of Crystal Growth, 1998, 191(3): 545-552. DOI: 10.1016/S0022-0248(98)00164-X |
| [61] | TSAI A P. Discovery of stable icosahedral quasicrystals: progress in understanding structure and properties[J]. Chemical Society Reviews, 2013, 44(34): 5352-5365. DOI: 10.1039/C3CS35388E |
| [62] | SOCOLAR J E S, LUBENSKY T C, STEINHARDT P J. Phonons, phasons, and dislocations in quasicrystals[J]. Physical Review B, 1986, 34(5): 3345-3360. DOI: 10.1103/PhysRevB.34.3345 |
| [63] | WOLLGARTEN M, BEYSS M, URBAN K, et al. Direct evidence for plastic-deformation of quasicrystals by means of a dislocation mechanism[J]. Physical Review Letters, 1993, 71(4): 549-552. DOI: 10.1103/PhysRevLett.71.549 |
| [64] | MOMPIOU F, BRESSON L, CORDIER P, et al. Dislocation climb and low-temperature plasticity of an Al-Pd-Mn quasicrystal[J]. Philosophical Magazine, 2003, 83(27): 3133-3157. DOI: 10.1080/1478643031000155110 |
| [65] | MESSERSCHMIDT U, BARTSCH M, FEUERBACHER M, et al. Friction mechanism of dislocation motion in icosahedral Al-Pd-Mn quasicrystals[J]. Philosophical Magazine A, 1999, 79(9): 2123-2135. DOI: 10.1080/01418619908210412 |
| [66] | TEXIER M, PROULT A, BONNEVILLE J, et al. Microstructure of I-Al-Pd-Mn deformed at low and intermediate temperatures[J]. Materials Science and Engineering: A, 2004, 387: 1023-1027. DOI: 10.1016/j.msea.2004.01.120 |
| [67] | ZOU Y, KUCZERA P, SOLOGUBENKO A, et al. Superior room-temperature ductility of typically brittle quasicrystals at small sizes[J]. Nature Communications, 2016(7): 12261. DOI: 10.1038/ncomms12261 |
| [68] | ZOU Y, KUCZERA P, STEURER W, et al. Disappearance of plastic anisotropy in decagonal quasicrystals at small scales and room temperature[J]. Extreme Mechanics Letters, 2016(8): 229-234. DOI: 10.1016/j.eml.2016.02.005 |
| [69] | SCHALL P, FEUERBACHER M, URBAN K. Plastic deformation of decagonal Al73Ni10Co17 single quasicrystals[J]. Philosophical Magazine, 2004, 84(7): 705-718. DOI: 10.1080/14786430310001624857 |
| [70] | FEUERBACHER A, SCHALL P. Plastic behaviour of decagonal Al-Ni-Co single quasicrystals[J]. Scripta Materialia, 2003, 49(1): 25-31. DOI: 10.1016/S0921-5093(00)01653-1 |
| [71] | LAPLANCHE G, BONNEVILLE J, JOULAIN A, et al. Mechanical properties of Al-Cu-Fe quasicrystalline and crystalline phases: An analogy[J]. Intermetallics, 2014, 50: 54-58. DOI: 10.1016/j.intermet.2014.02.004 |
| [72] | PARK J Y, OGLETREE D F, SALMERON M, et al. High frictional anisotropy of periodic and aperiodic directions on a quasicrystal surface[J]. Science, 2005, 309(5739): 1354-1356. DOI: 10.1126/science.1113239 |
| [73] | FILIPPOV A E, VANOSSI A, URBAKH M. Origin of friction anisotropy on a quasicrystal surface[J]. Physical review letters, 2010, 104(7): 074302. DOI: 10.1103/PhysRevLett.104.074302 |
| [74] | YE Z J, MARTINI A, THIEL P, et al. . Atomistic simulation of frictional anisotropy on quasicrystal approximant surfaces[J]. Physical Review B, 2016, 91(33): 4218-4229. DOI: 10.1103/PhysRevB.93.235438 |
| [75] | DUBOIS J M. Properties-and applications of quasicrystals and complex metallic alloys[J]. Chemical Society Reviews, 2012, 41(20): 6760-6777. DOI: 10.1039/C2CS35110B |
| [76] | STEIJN R P. Friction and wear of single crystals[J]. Wear, 1964, 7(1): 48-66. DOI: 10.1016/0043-1648(64)90078-X |
| [77] | DYER L D. Rolling friction on single crystals of copper in the plastic range[J]. Acta Metallurgica, 1961, 9(10): 928-936. DOI: 10.1016/0001-6160(61)90111-0 |
| [78] | BAILEY J M, GWATHMEY A T. Friction and surface deformation during sliding on a single crystal of copper[J]. Tribology Transactions, 1962, 5(1): 45-56. DOI: 10.1080/05698196208972452 |
| [79] | STEIJN R P. On the wear of sapphire[J]. Journal of Applied Physics, 1961, 32(10): 1951-1958. DOI: 10.1063/1.1728269 |
| [80] | BUCKLEY D H, JOHNSON R L. Friction and wear of hexagonal metals and alloys as related to crystal structure and lattice parameters in vacuum[J]. Tribology Transactions, 1966, 9(2): 121-135. DOI: 10.1080/05698196608972128 |
| [81] | BUCKLEY D H, JOHNSON R L. Influence of crystal structure on friction characteristics of rare-earth and related metals in vacuum to 10-10 mm of mercury[J]. Tribology Transactions, 1965, 8(2): 123-132. DOI: 10.1080/05698196508972086 |
| [82] | UCKLEY D H. The influence of the atomic nature of crystalline materials on friction[J]. Tribology Transactions, 1968, 11(2): 89-100. DOI: 10.1080/05698196808972212 |
| [83] | GRÖNING O, WIDMER R., RUFFIEUX P., et al. Scanning tunnelling microscopy with atomic resolution on the twofold surface of the icosahedral AlPdMn quasicrysta[J]. Philosophical Magazine, 2006, 86(6/7/8): 773-779. DOI: 10.1080/14786430500306535 |
| [84] | SHARMA H R, FOURNÉE V, SHIMODA M, et al. Structure of the fivefold surface of the icosahedral Al-Cu-Fe quasicrystal: experimental evidence of bulk truncations at larger interlayer spacings[J]. Physical Review Letters, 2004, 93(16): 165502. DOI: 10.1103/PhysRevLett.93.165502 |
| [85] | CAI T, SHI F, SHEN Z, et al. Structural aspects of the fivefold quasicrystalline Al-Cu-Fe surface from STM and dynamical LEED studies[J]. Surface Science, 2001, 495(1/2): 19-34. DOI: 10.1016/S0039-6028(01)01500-X |
| [86] | ROUXEL D, CAI T H, JENKS C J, et al. Structural aspects of the threefold surface of icosahedral Al-Pd-Mn[J]. Surface Science, 2000, 461(1): L521-L527. DOI: 10.1016/S0039-6028(00)00513-6 |
| [87] | SHEN Z, JENKS C J, ANDEREGG J, et al. Structure and stability of the twofold surface of icosahedral Al-Pd-Mn by low-energy electron diffraction and X-ray photoemission spectroscopy[J]. Physical Review Letters, 1997, 78(6): 1050-1053. DOI: 10.1103/PhysRevLett.78.1050 |
| [88] | TAMURA R, YADAV T P, MCLEOD I M, et al. Scanning tunneling microscopy of a polygrain Al-Pd-Re quasicrystal: study of the relative surface stability[J]. Journal of Physics Condensed Matter, 2013, 25(39): 395007. DOI: 10.1088/0953-8984/25/39/395007 |
| [89] | NUGENT P J, SMERDON J A, MCGRATH R, et al. Step-terrace morphology and reactivity to C60 of the five-fold icosahedral Ag-In-Yb quasicrystal[J]. Philosophical Magazine, 2011, 91(19/20/21): 2862-2869. DOI: 10.1080/14786435.2010.514870 |
| [90] | CUI C, NUGENT P J, SHIMODA M, et al. The atomic structure of the threefold surface of the icosahedral Ag-In-Yb quasicrystal[J]. Journal of Physics Condensed Matter, 2012, 24(44): 445011. DOI: 10.1088/0953-8984/24/44/445011 |
| [91] | CUI C, NUGENT P J, SHIMODA M, et al. Structure of the twofold surface of the icosahedral Ag-In-Yb quasicrystal[J]. Journal of Physics: Condensed Matter, 2013, 26(1): 015001. DOI: 10.1088/0953-8984/26/1/015001 |
| [92] | PARK J Y, OGLETREE D F, SALMERON M, et al. Atomic scale coexistence of periodic and quasiperiodic order in a 2-fold Al-Ni-Co decagonal quasicrystal surface[J]. Physical Review B, 2005, 72(22): 220201. DOI: 10.1103/PhysRevB.72.220201 |
| [93] | TAKAKURA H, YAMAMOTO A, TSAI A P. The structure of a decagonal Al72Ni20Co8 quasicrystal[J]. Acta Crystallographica, 2001, 57(57): 576-585. DOI: 10.1107/S0108767301007942 |
| [94] | LEDIEU J, HOEFT J T, REID D E, et al. Copper adsorption on the fivefold Al70Pd21Mn9, quasicrystal surface[J]. Physical Review B, 2005, 72(3): 035420. DOI: 10.1103/PhysRevB.72.035420 |
| [95] | LEDIEU J. Ordering of Si atoms on the fivefold Al-Pd-Mn quasicrystal surface[J]. Physical Review B, 2006, 73(1): 012204. DOI: 10.1103/PhysRevB.73.012204 |
| [96] | KRAJČÍC M, HAFNER J. Structure, stability, and electronic properties of the, i -AlPdMn quasicrystalline surface[J]. Physical Review B, 2005, 71(71): 054202. DOI: 10.1103/PhysRevB.71.054202 |
| [97] | LEDIEU J, LEUNG L, WEARING L H, et al. Self-assembly, structure and electronic properties of a quasiperiodic lead monolayer[J]. Physical Review B, 2008, 77(7): 439-446. DOI: 10.1103/PhysRevB.77.073409 |
| [98] | MARTIN S, HEBARD A F, KORTAN A R, et al. Transport properties of Al65Cu15Co20, and Al70Ni15Co15, decagonal quasicrystals[J]. Physical Review Letters, 1991, 67(6): 719-722. DOI: 10.1103/PhysRevLett.67.719 |
| [99] | SMONTARA A, IVKOV J. Anisotropic magnetic, electrical, and thermal transport properties of the Y-Al-Ni-Co decagonal approximant[J]. Physical Review B Condensed Matter, 2008, 78(10): 104204. DOI: 10.1103/PhysRevB.78.104204 |
| [100] | BOBNAR M, JEGLI P, KLANJŠEK M, et al. Intrinsic anisotropic magnetic, electrical, and thermal transport properties of d-Al-Co-Ni decagonal quasicrystals[J]. Physical Review B Condensed Matter, 2012, 85(2): 024205. DOI: 10.1103/PhysRevB.85.024205 |
| [101] | DOLINŠEK J. Extrinsic origin of the insulating behavior of polygrain icosahedral Al-Pd-Re quasicrystals[J]. Physical Review B, 2006, 74(13): 134201. DOI: 10.1103/PhysRevB.74.134201 |
| [102] | BOBNAR M, VRTNIK S, JAGLIČIČ Z, et al. Electrical, magnetic, and thermal properties of the single-grain Ag42In42Yb16 icosahedral quasicrystal: Experiment and modeling[J]. Physical Review B Condensed Matter, 2011, 84(13): 4578-4586. DOI: 10.1103/PhysRevB.84.134205 |
| [103] |
范天佑.
固体与软物质准晶数学弹性与相关理论及应用[M]. 北京: 北京理工大学出版社, 2014: 51-271.
FAN Tianyou. Mathematical theory of elasticity and relevant topics of solid and solft-matter quasicrystals and its applications[M]. Beijing: Beijing Institute of Technology Press, 2014: 51-271. |
| [104] | BUNZ D, ZEGER G, ROTH J, et al. Molecular dynamic studies of atomic jumps in d-Al-Cu-Co[J]. Materials Science and Engineering a-Structural Materials Properties Microstructure and Processing, 2000, 294: 675-679. DOI: 10.1016/S0921-5093(00)01187-4 |
| [105] | TREBIN H R, MIKULLA R, STADLER J, et al. Molecular dyna-mics simulations of crack propagation in quasicrystals[J]. Computer Physics Communications, 1999, 121: 536-539. DOI: 10.1016/S0010-4655(99)00400-2 |
| [106] | SCHAAF G D, ROTH J, TREBIN H R. Numerical simulation of dislocation motion in three-dimensional icosahedral quasicrystals[J]. Philosophical Magazine a-Physics of Condensed Matter Structure Defects and Mechanical Properties, 2000, 80(7): 1657-1668. DOI: 10.1080/01418610008212142 |
| [107] | RUDHART C, RÖSCH F, GÄHLER F, et al. Crack propagation in icosahedral model quasicrystals[J]. High Performance Computing in Science & Engineering, 2003: 107-116. DOI: 10.1007/978-3-642-55876-4_8 |
| [108] | SCHAAF G D, ROTH J, TREBIN H R. Dislocation motion in icosahedral quasicrystals at elevated temperatures: numerical simulation[J]. Philosophical Magazine, 2003, 83(21): 2449-2465. DOI: 10.1080/0141861031000113352 |
| [109] | RUDHART C, TREBIN H R, GUMBSCH P. Crack propagation in perfectly ordered and random tiling quasicrystals[J]. Journal of Non-Crystalline Solids, 2004, 334: 453-456. DOI: 10.1016/j.jnoncrysol.2003.12.039 |
| [110] | ROSCH F, RUDHART C, ROTH J, et al. Dynamic fracture of icosahedral model quasicrystals: A molecular dynamics study[J]. Physical Review B, 2005, 72(1): 014128. DOI: 10.1103/PhysRevB.72.014128 |
| [111] | SASAJIMA Y, TANAKA H, ITABA M, et al. Computer experiments of fracture of 2-dimensional henley-elser type quasi-crystals[J]. Materials Science and Engineering a-Structural Materials Properties Microstructure and Processing, 1994, 176(1/2): 283-288. DOI: 10.1016/0921-5093(94)90987-3 |
| [112] | TREBIN H R, MIKULLA R, ROTH J. Motion of dislocations in two-dimensional decagonal quasicrystals[J]. Journal of non-crystalline so-lids, 1993, 153: 272-275. DOI: 10.1016/0022-3093(93)90356-3 |
| [113] | ENGEL M, UMEZAKI M, TREBIN H R, et al. Dynamics of particle flips in two-dimensional quasicrystals[J]. Physical Review B Condensed Matter, 2010, 82(13): 087201. DOI: 10.1103/PhysRevB.82.134206 |
| [114] | YANG L Z, HE F M, GAO Y. Finite element method for static problems of cubic quasicrystals[J]. Acta Physica Polonica, 2014, 126(2): 471-473. DOI: 10.12693/APhysPolA.126.471 |
| [115] |
杨连枝, 何蕃民, 高阳, 等. 二十面体Al-Pd-Mn准晶板的断裂行为研究[C]//北京力学会第20届学术年会论文集. 北京: 中国学术期刊电子出版社, 2014: .
YANG Lianzhi, HE Fanmin, GAO Yang, et al. Study of frature behavior of icosahedral Al-Pd-Mn quasicrystal slab[C]// The Proceedings of the 20th Annual Conference of Beijing Society of Theoretical and Applied Mechanics. Beijing: China Academic Journal Electronic Publishing House, 2014. |
| [116] |
吴祥法, 范天佑, 安冬梅. 用路径守恒积分计算平面准晶裂纹扩展的能量释放率[J].
计算力学学报, 2000, 17(1): 34-42.
WU Xiangfa, FAN Tianyou, AN Dongmei. Energy release rate of plane quasicrystals with crack determined by path-independent E-integral[J]. Chinese Journal of Computational Mechanics, 2000, 17(1): 34-42. DOI: 10.3969/j.issn.1007-4708.2000.01.006 |
| [117] | AMADA T, TAKAKURA H, EUCHNER H, et al. Atomic structure and phason modes of the Sc-Zn icosahedral quasicrystal[J]. Iucrj, 2016(3): 247-258. DOI: 10.1107/S2052252516007041 |
| [118] | YAMADA T, TAKAKURA H, KONG T, et al. Atomic structure of the i-R-Cd quasicrystals and consequences for magnetism[J]. Physical Review B, 2016, 94(6): 060103. DOI: 10.1103/PhysRevB.94.060103 |
| [119] | KENZARI S, BONINA D, DUBOIS J M, et al. Quasicrystal-polymer composites for selective laser sintering technology[J]. Materials & Design, 2012, 35: 691-695. DOI: 10.1016/j.matdes.2011.10.032 |
 2017, Vol. 49
2017, Vol. 49