动态稳定性是研究跳跃机器人的关键问题之一,落地冲击对单足机器人跳跃运动的动态稳定性影响最大,国内外学者近年所推出的多款单足机器人样机如Raibert机器人[1]、弓形腿机器人[2]、ARL-Monopod[3-4]和仿袋鼠机器人[5-6]均采用忽略弹跳腿质量的SLIP模型来回避碰撞冲击力的影响.对于本文所设计的弹跳腿质量达到机器人总质量三分之一的全气动单足机器人[7],必须掌握机器人落地碰撞冲击力的产生机理和变化规律,为研究机器人动态稳定性奠定基础.目前,广泛采用的动量冲量法[8]不考虑碰撞的中间过程且速度恢复系数难以准确估算[9]; 有限元法[10]由于自由度过多导致计算效率低,并且在处理大范围运动与小范围振动耦合的问题时,容易产生数值病态解问题; 连续接触力法[11]中基于Hertz接触理论及恢复系数的非线性弹簧阻尼模型,必须满足碰撞体局部小变形的前提条件[12].
本文所设计的单足机器人采用橡胶地面进行碰撞过程的缓冲,在机器人刚性足底和橡胶压缩大变形的条件下,通过建立橡胶非线性弹簧阻尼模型,采用连续接触力法构建单足机器人落地碰撞模型,运用理论分析、动态建模、数值仿真和实验验证相结合的研究方法,研究碰撞冲击力的变化规律及相关因素的影响规律.
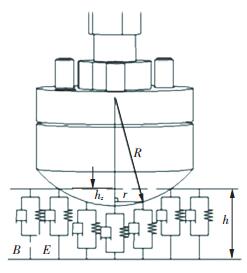
1 单足机器人落地碰撞过程分析单足机器人垂直跳跃落地碰撞过程见图 1. 图 1(a)所示机器人位于最高点位置,控制气缸上下腔气压相等和活塞相对缸体在确定位置,令单足机器人沿垂直滑道自由下落. 图 1(b)为机器人落地碰撞过程原理、受力分析及坐标系示意图,相对坐标系OtjZtj原点在地面坐标系OZ中的坐标为H-ztj,角标t、j和tj分别表示支撑腿、机身和支撑腿相对机身的量.机器人落地后,支撑腿在橡胶地面冲击反力Fc、重力mtg、活塞与缸筒摩擦力Fm、两腔气压差推力(p1-p2)A1的共同作用下,速度由初值快速减小为零并发生反弹,反弹阶段由于两腔气压差的更大推力,支撑腿离开地面很小的距离又再次下降,与地面形成二次碰撞.机身在足底触地时刻上下腔气压差推力为零,保持自由落体运动状态不参与碰撞,碰撞期间在两腔气压差推力、重力mjg和摩擦力作用下加速度略有降低.

|
图 1 机器人结构及受力分析 Figure 1 Diagram of the robot and dynamics analysis model |
由于高弹性橡胶地面的缓冲作用延长了碰撞时间,橡胶地面的冲击反力可以通过其较大的变形计算,拟通过建立支撑腿和机身的运动方程、两腔气体能量方程、橡胶变形力计算方程构建机器人落地碰撞数学模型[13].
2.1 支撑腿和机身运动方程根据图 1(b)机器人落地碰撞过程受力分析,可得支撑腿和机身动力学方程为
| $ \begin{array}{l} \frac{{{{\rm{d}}^2}{z_{\rm{t}}}}}{{{\rm{d}}{t^2}}} = \frac{1}{{{m_{\rm{t}}}}}\left( {{p_2}{A_1} - {p_1}{A_1} - {m_{\rm{t}}}g - {F_{\rm{m}}} + {F_{\rm{c}}}} \right),\\ \frac{{{{\rm{d}}^2}{z_{\rm{j}}}}}{{{\rm{d}}{t^2}}} = \frac{1}{{{m_{\rm{j}}}}}\left( {{p_1}{A_1} - {p_2}{A_1} - {m_{\rm{j}}}g + {F_{\rm{m}}}} \right). \end{array} $ |
式中:zt为支撑腿质心绝对坐标,A1为活塞受压面积,zj为机身质心绝对坐标.
摩擦力在气缸运动过程中变化非常复杂,在有润滑的条件下,一般将其视为由定值静摩擦力和动摩擦力及与活塞速度成正比的黏性摩擦力组成.考虑到支撑腿相对机身一直处于运动之中,且碰撞时间较短,故不考虑静摩擦力,摩擦力计算公式为
| $ {F_{\rm{m}}} = {F_{\rm{K}}} \cdot {\rm{sign}}\left( v \right) + {B_1}v, $ |
式中:B1为黏性系数,FK为库伦摩擦力,v为活塞相对缸筒速度.
| $ v = \frac{{{\rm{d}}{z_{\rm{t}}}}}{{{\rm{d}}t}} - \frac{{{\rm{d}}{z_{\rm{j}}}}}{{{\rm{d}}t}}, $ |
由于气缸两腔气体压力较低,碰撞时间极短,假设碰撞期间气体的热力过程为理想气体的绝热过程,根据热力学第一定律及绝热过程状态参数的关系,可得上下腔封闭容腔能量方程为
| $ \begin{array}{*{20}{c}} {{p_1} = {p_{11}}{{\left( {\frac{{{V_{11}}}}{{{V_1}}}} \right)}^k} = {p_{11}}{{\left( {\frac{{s - {z_{{\rm{tj1}}}}}}{{s - {z_{{\rm{tj}}}}}}} \right)}^k},}\\ {{p_2} = {p_{21}}{{\left( {\frac{{{V_{21}}}}{{{V_2}}}} \right)}^k} = {p_{21}}{{\left( {\frac{{{z_{{\rm{tj1}}}}}}{{{z_{{\rm{tj}}}}}}} \right)}^k}.} \end{array} $ |
式中:p、V、s、ztj、k分别为腔内气体绝对压力、体积、气缸行程、支撑腿相对机身坐标、比热比,p、V的第1个角标为“1”或“2”分别表示气缸上、下腔参数,p、V的第2个角标和ztj的第1个角标为“1”表示机器人落地时刻初始参数.
2.3 橡胶力学模型橡胶垫可以视为弹性地基模型[14],忽略剪切应力,考虑到橡胶的黏弹特性,建立橡胶地面的力学模型如图 2所示.
|
图 2 接触力学模型 Figure 2 Contact force model |
橡胶材料的应力与应变关系如下:
| $ \sigma = E'\varepsilon + B{\rm{d}}\varepsilon /{\rm{d}}t. $ |
式中:E′为橡胶贮能模量,B为橡胶阻尼系数,σ、ε分别为橡胶的应力和应变.
对于橡胶应力应变模型,当应变<10%时,贮能模量通常认为是常数,当应变>10%时,贮能模量呈现非线性变化.实验用橡胶垫采用减振性能较强的丁腈橡胶,在碰撞过程中,应变在30%左右.文献[15-16]根据热力学统计原理,在准静态试验条件下,橡胶弹性应力与应变的关系为
| $ \begin{array}{l} \sigma = \frac{a}{3}\frac{{\left( {{\varepsilon ^2} - 3\varepsilon + 3} \right)}}{{{{\left( {1 - \varepsilon } \right)}^2}}}\varepsilon ,\\ E' = \frac{a}{3}\frac{{\left( {{\varepsilon ^2} - 3\varepsilon + 3} \right)}}{{{{\left( {1 - \varepsilon } \right)}^2}}}. \end{array} $ |
式中a为实验测得的橡胶小变形贮能模量.
机器人落地碰撞阶段,橡胶处于动态变化过程.典型橡胶在室温条件下,频率每扩大10倍,贮能模量增加10%[17],
| $ E' = \frac{a}{3}\frac{{\left( {{\varepsilon ^2} - 3\varepsilon + 3} \right)}}{{{{\left( {1 - \varepsilon } \right)}^2}}} \times {1.1^{\frac{f}{{10}}}}, $ |
式中f为橡胶振动频率.
| $ \begin{array}{*{20}{c}} {\tan \delta = \frac{{E''}}{{E'}},}\\ {\tan \delta = n \cdot f,}\\ {B = \frac{{E''}}{{2{\rm{\pi }}f}} = \frac{b}{{6{\rm{\pi }}}}\frac{{\left( {{\varepsilon ^2} - 3\varepsilon + 3} \right)}}{{{{\left( {1 - \varepsilon } \right)}^2}}} \times {{1.1}^{\frac{f}{{10}}}}.} \end{array} $ |
式中:E″为耗能模量,δ为应变滞后应力的相位角,tan δ为耗能因子,与橡胶振动频率成正比,n为与橡胶材料有关的常数,b=n×a.
碰撞力为橡胶地面变形微元作用力在变形面积上的积分,橡胶变形呈现与球面足底相同的形状,在相同的半径上具有相同的变形量,取环形微元面积为
| $ {\rm{d}}A = 2{\rm{\pi }}r{\rm{d}}r. $ |
式中:r为微圆环的内径,等于应力作用点到支撑腿轴线的距离.
由图 2可得最大作用半径rmax为
| $ {r_{\max }} = \sqrt {{R^2} - {{\left( {R - {h_{\rm{z}}}} \right)}^2}} . $ |
式中:R为机器人足底球面半径,hz为机器人足底压入橡胶地面的深度.
以机器人落地时刻为起点,机器人足底压入深度为
| $ \int_0^t {{v_{\rm{t}}}{\rm{d}}t} = - {h_{\rm{z}}}, $ |
式中vt为支撑腿绝对速度.
距离支撑腿轴线为r的微圆环应变为
| $ \varepsilon = \frac{{\sqrt {{R^2} - {r^2}} - \left( {R - {h_{\rm{z}}}} \right)}}{h}, $ |
式中h为橡胶垫厚度.
机器人落地受到的碰撞力为微圆环上作用力在整个作用面积上的积分.
| $ {F_{\rm{c}}} = \int_0^{{r_{\max }}} {2{\rm{\pi }}r\sigma {\rm{d}}r} . $ |
对单足跳跃机器人垂直落地碰撞过程,在MATLAB/simulink建立仿真模型.机器人系统和橡胶垫参数分别取表 1和表 2所示初值. z0为机器人下落高度.
| 表 1 机器人系统参数初值表 Table 1 Initial value of parameters of robot system |
| 表 2 橡胶垫参数初值表 Table 2 Initial value of parameters of rubber mat |
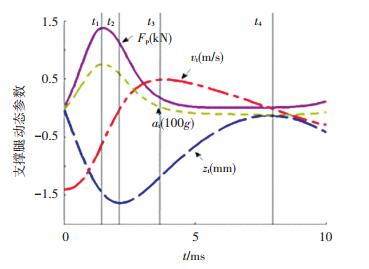
当机器人相关初始参数取表 1和表 2中数据时,单足跳跃机器人落地碰撞过程中,支撑腿动态参数仿真曲线如图 3所示,at为支撑腿绝对加速度.
|
图 3 机器人从0.1 m高度落地碰撞动态参数曲线 Figure 3 Simulation result of the robot for 0.1m free fall |
机器人落地碰撞过程包括压缩阶段和恢复阶段.在压缩阶段,支撑腿足底表面与橡胶表面始终接触,支撑腿运动速度等于橡胶变形速度.随着机器人足底压入深度增大,橡胶地面快速增加的弹性力与较大阻尼力合成的冲击力快速增大,在t1时刻,冲击力达到最大值1 369.4 N.随着支撑腿下降速度的快速减小,阻尼力减小速度开始大于弹性力增加速度,冲击力开始减小.至t2时刻,支撑腿速度减小到零,冲击力为1 094.8 N.机器人足部压入橡胶垫深度达到最大值1.63 mm,弹性力达到最大,阻尼力为零,冲击力完全由弹性力提供.支撑腿到达最低点后,进入恢复阶段并在冲击反力、重力、两腔气压差推力和摩擦力等阻力的综合作用下开始向上做加速运动.随着支撑腿的反弹,弹性力快速减小,阻尼力反向增大.在t3时刻,支撑腿反弹速度达到最大值0.49 m/s,橡胶变形1.14 mm.在t3~t4段,支撑腿反弹速度逐渐减小,在t4时刻,支撑腿反弹至最高点-0.13 mm,碰撞过程结束.
3.2 冲击力影响因素仿真分析 3.2.1 机器人下落高度对冲击力的影响机器人系统取表 1和表 2所示初值,令机器人下落高度分别为0.05、0.10、0.15和0.20 m,碰撞过程特征时刻仿真数据如表 3所示.
| 表 3 下落高度影响规律仿真数据 Table 3 Simulation data under different falling height |
下落高度增加使机器人落地速度增加,导致碰撞冲击力和橡胶最大变形单调增加.当下落高度由0.05 m增加至0.20 m时,由于冲击反力相对增加量174%大于橡胶最大变形相对增加量28.6%,导致碰撞时间单调减小.支撑腿反弹阶段,冲击反力克服重力、上下腔气压差推力和阻尼力推动支撑腿向上加速运动; 当下降高度<0.15 m时,相对更大的阻力使支撑腿在足底未到达橡胶表面时速度减小到0,反弹最高点冲击力随下落高度的增加单调减小; 下落高度为0.20 m时,足够大的冲击反力使支撑腿跳离地面,反弹最高点冲击力为0.
3.2.2 橡胶垫厚度对冲击力的影响机器人系统取表 1和表 2所示初值,令橡胶垫厚度分别为3.0、4.0、4.5、和5.0 mm.机器人在不同厚度橡胶垫缓冲条件下碰撞过程特征时刻仿真数据如表 4所示.
| 表 4 橡胶垫厚度影响规律仿真数据 Table 4 Simulation data under different the thickness of the rubber mat |
橡胶贮能模量随应变单调增加.随着橡胶垫厚度的增加,橡胶垫缓冲能力更强,吸收支撑腿落地时刻相同的动能需要更大的变形,最大冲击力相应减小.更小的冲击力和更大的变形量综合作用,使反弹最高点冲击力和碰撞时间均单调增加.
3.2.3 足底球面半径对冲击力的影响机器人系统取表 1和表 2所示初值,令机器人足底球面半径取表 5第1列数据.对足底球面半径不同的机器人进行落地碰撞过程仿真,碰撞过程特征时刻仿真数据如表 5所示.
| 表 5 足底球面半径影响规律仿真数据 Table 5 Simulation data under the different radius of the surface profile of the foot |
足底球面半径增大使橡胶变形面积增加,橡胶垫相同应变下产生更大的冲击力.随着足底球面半径的增加,吸收支撑腿落地时刻相同的动能需要更小的橡胶垫变形、更小的最大应变使最大冲击力减小,橡胶垫更大的变形面积和更小的应变共同作用,导致最大冲击力变化很小.最大冲击力的微小变化使反弹最高点冲击力变化不大,变化不大的冲击力和更小的最大变形量使碰撞时间单调减小.
3.2.4 橡胶材料特性对冲击力的影响机器人系统取表 1和表 2所示初值,令模型中的橡胶小变形贮能模量a分别为1.0、1.5、2.0和2.5 MPa,机器人与不同模量的橡胶垫发生落地碰撞时,碰撞过程特征时刻仿真数据如表 6所示.
| 表 6 橡胶模量a影响规律仿真数据 Table 6 Simulation data under the different parameters a of rubber |
橡胶模量增加使贮能模量和黏性阻尼系数均单调增加,橡胶垫缓冲能力下降.随着橡胶模量的增加,最大冲击力单调增加.吸收支撑腿落地时刻相同的动能,需要更小的橡胶垫变形.橡胶垫更大的冲击反力和更小的变形共同作用,使反弹最高点冲击力单调增加,碰撞时间单调减小.
机器人系统取表 1所示初值,令橡胶材料耗能因子与频率的比值n分别为0.005、0.010、0.015和0.020.机器人与参数n不同的橡胶垫发生落地碰撞时,碰撞过程特征时刻仿真数据如表 7所示.
| 表 7 橡胶参数n影响规律仿真数据 Table 7 Simulation data under the different parameters n of rubber |
橡胶参数n增大使阻尼力单调增大.随着橡胶参数n的增大,压缩阶段初期支撑腿更大的速度产生更大的阻尼力,使支撑腿速度下降得更快,导致橡胶垫最大变形单调减小.更小的弹性力与更大的阻尼力使支撑腿接近最低点的最大冲击力出现先减小后增加的变化趋势.反弹阶段更大的阻尼力使反弹最高点冲击力快速增加,更小的橡胶变形和反弹位移与冲击力共同作用,使碰撞时间呈现与最大冲击力相反的变化趋势.当n=0.005时,由于阻尼力较小,机器人在5.7 ms后开始二次腾空.
4 垂直跳跃落地碰撞实验 4.1 实验台介绍单足机器人垂直跳跃实验台结构原理如图 1(a)所示,实验台照片如图 4所示,该机器人高0.85 m.

|
图 4 单足垂直跳跃机器人实验平台 Figure 4 Experiment table of the vertical constrained one-legged robot |
实验台主要元器件如表 8所示,其中活塞相对位移传感器采用伺服气缸内部集成的位移传感器,位置检测精度为0.001 mm.
| 表 8 实验台主要元件清单 Table 8 The equipment list of experiment table |
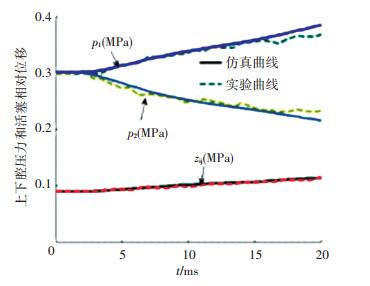
机器人实验系统各参数取表 1所示初值,令气缸上下腔封闭,机器人从0.1 m的高度自由下落,取机器人落地时刻作为碰撞过程的起始点. 图 5为根据实测数据绘制的活塞相对位移和两腔气压曲线与仿真曲线比较图.
|
图 5 机器人自0.1 m落下实验与仿真数据 Figure 5 Experimental data and simulation data of the robot for 0.1 m free fall |
由图 5可以看出,各参数具有相同的变化规律,活塞相对位移、上下腔气压最大相对误差分别为4.2%、7.6%和5.5%.
根据碰撞过程两腔气压实测数据,使用机身运动方程可计算出机身运动规律,根据活塞相对机身位移数据可计算出支撑腿绝对位移和速度,借助支撑腿速度可计算出冲击力.根据实验数据计算的机器人落地碰撞过程动态参数实验曲线如图 6.

|
图 6 机器人自0.1 m落下支撑腿实验曲线 Figure 6 Experiment result of the robot for 0.1m free fall |
比较图 6和图 3,各动态参数具有相同的变化规律,由于对实验数据进行了滤波处理,实验冲击力的峰值略小于仿真曲线中的对应值,最大冲击力相对误差10.1%,最大速度相对误差2.3%,最大位移相对误差7.3%,实验结果验证了单足机器人落地碰撞模型和仿真结果的正确性.
5 结论1) 针对垂直跳跃单足机器人球面尼龙足底与橡胶地面的碰撞过程,建立了由支撑腿和机身的动力学模型、橡胶地面大变形黏弹性力学模型和气缸上下腔气体热力学模型组成的整体数学模型.
2) 建立了机器人落地碰撞过程MATLAB仿真模型.仿真结果表明,压缩阶段递增的弹性力和先增后减的阻尼力使地面冲击反力先增大后减小,恢复阶段快速减小的弹性力和反向阻尼力共同作用导致冲击反力单调减小.最大冲击力随下落高度、橡胶贮能模量的增大和橡胶垫厚度的减小单调增大,随橡胶耗能因子与频率比值的增大先减小后增大.
3) 搭建了单足机器人垂直跳跃落地碰撞实验台,0.1 m下落高度的实验结果与仿真结果吻合良好,证明本文所做的理论分析、数学模型和仿真结果是正确的,为研究单足机器人自由跳跃时落地过程和全跳跃周期动态稳定性奠定了必要的基础.
| [1] | RAIBER M H. Legged robots that balance[J]. IEEE Expert, 1986, 1(4): 89-89. DOI: 10.1109/MEX.1986.4307016 |
| [2] | ZEGLIN G. The bow leg hopping robot [D]. Pittsburgh: Camegie Mellon University, 1999. DOI: 10.1109/ROBOT.1998.677082. |
| [3] | GREGORIO P, AHMADI M, BUEHLER M. Design, control, andenergetics of an electrically actuated legged robot[J]. IEEE Transactions on Systems Man and Cybernetics, 1997, 27(4): 626-634. DOI: 10.1109/3477.604106 |
| [4] | AHMADIM, BUEHLER M. Controlled passive dynamic running experiments with the ARL-Monopod Ⅱ[J]. IEEE Transactions on Robotics, 2006, 22(5): 974-986. DOI: 10.1109/TRO.2006.878935 |
| [5] | ZEGLING J. Uniroo: a one legged dynamic hopping robot [D]. Cambridge: Massachusetts Institute of Technology, 1991. |
| [6] |
葛文杰, 夏旭峰, 黄杰, 等. 基于双质量弹簧模型的仿袋鼠机器人间歇跳跃落地稳定性研究[J].
西北工业大学学报, 2007, 25(4): 517-522.
GE Wenjie, XIA Xufeng, HUANG Jie, et al. Exploring gait stability of kangaroo robot based on two-mass-one-spring model in intermittent touchdown phase[J]. Journal of North western Polytechnical University, 2007, 25(4): 517-522. DOI: 10.3969/j.issn.1000-2758.2007.04.011 |
| [7] |
李哲, 苏兴旺, 阎宏伟, 等. 气动弹跳腿垂直方向稳定跳跃研究[J].
机器人, 2013, 35(3): 306-312.
LI Z, SU X W, YAN H W, et al. Stable hopping of a pneumatically actuated leg in vertical direction[J]. Jiqiren/robot, 2013, 35(3): 306-312. DOI: 10.3724/SP.J.1218.2013.00306 |
| [8] | WAGGD J. A note on coefficient of restitution models including the effects of impact induced vibration[J]. Journal of Sound and Vibration, 2007, 300(3/4/5): 1071-1078. DOI: 10.1016/j.jsv.2006.08.030 |
| [9] | YAO Wenli, CHEN Bin, LIU Caishan. Energetic coefficient of restitution for planar impact in multi-rigid-body systems with friction[J]. International Journal of Impact Engineering, 2005, 31(3): 255-265. DOI: 10.1016/j.ijimpeng.2003.12.007 |
| [10] | BOGRADS, REUSS P, SCHMIDT A. Modeling the dynamics of mechanical joints[J]. Mechanical Systems and Signal Processing, 2011, 25(8): 2801-2826. DOI: 10.1016/j.ymssp.2011.01.010 |
| [11] | HUNT K H, CROSSLEY F R E. Coefficient of restitution interpreted as damping in vibroimpact[J]. Journal of Applied Mechanics, 1975, 42(2): 440-445. DOI: 10.1115/1.3423596 |
| [12] | LANKARANIH M, NIKRAVESH P E. A contact force model with hysteresis damping for impact analysis of multibody systems[J]. Journal of Mechanical Design, 1990, 112(3): 369-376. DOI: 10.1115/1.2912617 |
| [13] | LI Zhe, YAN Hongwei, JI Jun. On dynamic characteristics of the vertical hopping of the one-legged robot[J]. Jiqiren/robot, 2015, 37(4): 467-477. DOI: 10.13973/j.cnki.robot.2015.0467 |
| [14] | FLORES P, MACHADO M, SILVA M T. On the continuous contact force models for soft materials in multibody dynamics[J]. Multibody System Dynamics, 2011, 25(25): 357-375. DOI: 10.1007/s11044-010-9237-4 |
| [15] |
中国国家标准化管理委员会. 硫化橡胶或热塑性橡胶压缩应力应变性能的测定: GB/T 7757—2009/ISO 7743[S]. 北京: 中国标准出版社, 2009.
Standardization Administration of the People's Republic of China. Rubber, vulcanized or thermoplastic determination of compression stress-strain properties: GB/T 7757—2009/ISO7743[S]. Beijing: Standards Press of China, 2009. |
| [16] | TRELOAR L R G. The elasticity of a network of long-chain molecules[J]. Transactions of the Faraday Society, 1946, 42(4): 83-94. DOI: 10.1039/tf9433900241 |
| [17] |
布朗, 张秀英. 橡胶的动态应力应变性能[J].
炭黑工业, 1998(6): 24-29.
BROWN R P, ZHANG X Y. Dynamic stress and strain of rubber[J]. Carbon Black Industry, 1998(6): 24-29. |
 2017, Vol. 49
2017, Vol. 49


