将超声加工与研磨和抛光技术相结合对不同材料进行研抛加工[1-4],可使材料去除率大大提高,表面加工质量也有不同程度提高.杨卫平[5]在化学机械抛光(CMP)的基础上施加椭圆超声波振动,使单晶硅的材料去除率提高了22%,抛光后的单晶硅表面形貌得到明显改善. Pandey等[6]应用超声辅助磁性磨料加工技术抛光不锈钢,能快速获得纳米级的超精密加工表面. Zhao等[7]利用超声振动辅助抛光技术,实现了SiC微圆柱表面的超精密加工,通过和无超声振动的传统抛光进行系统的比较研究,分析了SiC表面的去除机理. Xu等[8-9]对蓝宝石进行了超声-化学机械抛光(UFV-CMP)实验研究,引入超声辅助抛光后, 相比于传统的化学机械抛光, 蓝宝石的去除率提高了近一倍,表面平整度误差也大大降低; 研究蓝宝石试件、抛光垫和磨粒在抛光过程中的相互作用发现:磨粒的运动速度与冲击作用会因超声振动而迅速增强,是去除蓝宝石表面材料的主要因素; 通过无磨粒抛光液中的超声振动实验,证明了超声空蚀对蓝宝石材料的去除作用; 空化效应会产生很强的爆破压力,反复作用在试件表面的压力也会加速材料去除.因此研究超声加工过程中的空化效应具有重要的理论和现实意义.一些学者研究了单空泡在超声作用下的时变特征[10-12].祝锡晶等[11-12]在对功率超声珩磨切削运动以及空化效应基本理论分析的基础上,以单个空化泡为研究对象,利用能量守恒定律,建立功率超声珩磨单个空化泡的动力学模型.模拟了不同超声条件(声压幅值、空泡初始半径、振动频率)对泡壁的运动以及运动速度的影响.孙冰等[13]利用计算流体力学软件FLUENT对磁致伸缩超声振动仪中超声空化发生特性进行了数值模拟,证明试样中间区域为主要空化区域,边缘区域发生空化的概率很小. Sajjadi等[14]研究了超声能场对流体介质中的声冲流及微小气泡的影响,结果证明,超声振动的功率每增大100 W,气泡总体积上升4.95%,声冲流的速度由29 cm/s上升到119 cm/s. Skoczypiec[15]分析了超声辅助-电化学抛光过程中的材料去除机理,证明超声振动可以加快化学溶解、减小电极极化.
为分析超声辅助抛光过程中研抛液的流体特性,本文分别对光滑及多孔抛光垫建立了不同膜厚尺度下超声振动抛光过程的FLUENT仿真模型.仿真分析了不同变量对流体的压力分布、速度分布、气相分布等特性的影响规律,为分析超声辅助抛光机理和提高试件表面的材料去除率提供理论指导.
1 超声振动对厚膜流体性能的影响 1.1 模型建立首先建立试件与抛光盘间的厚膜超声作用模型,如图 1所示.在直径50 mm的上试件和下研抛盘间充满研抛液,试件在纵向做超声振动,最大位移60 μm,频率20 000 Hz.

|
图 1 厚膜下的超声作用模型 Figure 1 Simulation model of thick-film on ultrasonic wave |
在Gambit软件中建立仿真模型,模型采用矩形网格.将试件下表面设为速度入口,出口设为压力出口.根据超声振动的频率与位移,可得入口速度方程为
| $ v = - 3.77 \times \sin \left( {40\;000\pi t} \right). $ |
式中,v为流体速度(m/s),t为时间(s).
由该速度入口边界条件,设定时间步长为1 μs, 每步迭代20次,收敛后进行后处理,即可分析一个周期中各典型时间节点的流体特征.
1.2 速度分布在超声振动的一个周期(τ)中,试件由初始位置开始振动,典型的4个不同时刻流体的速度变化流线如图 2所示.
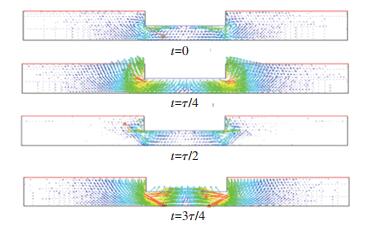
|
图 2 不同时刻液膜流体流线图 Figure 2 Streamline diagram of ultrasonic model at different time |
图 3为各时刻表面处流体在水平(X)和垂直(Y)方向的速度变化.可以看出,一个周期中,流场的纵向速度矢量是关于中心时刻对称的,符合入口边界条件的设定.在各个时间节点的纵向速度矢量均相对于流场中线左右对称.流体的纵向速度在试件表面非常稳定,但在试件边缘发生突变,数值超过入口峰值且形成反向流.

|
图 3 研抛表面流体速度分布曲线 Figure 3 Streamline diagram of ultrasonic model at different time |
流场横向速度矢量也符合关于中心时刻对称、关于流场中线对称的规律,由试件中心向外,其数值呈线性增大趋势,在试件边缘处骤增,最高达到6 m/s,由边缘向外,横向速度矢量的数值快速降低.超声振动明显增强了流场的流动性.研磨液的横向流动有利于去除试件表面材料,更新流场的研磨液.
1.3 压力分布计算域流体在4个典型时刻的压力分布如图 4所示.同流场的速度变化类似,流体压力在一个周期中也存在对称的正负交替变化规律.
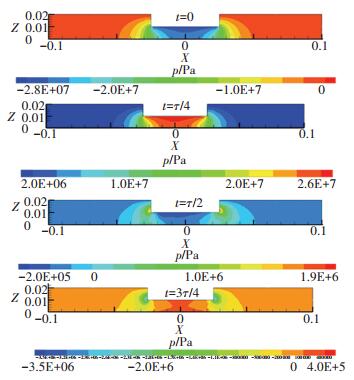
|
图 4 不同时刻流体压力云图 Figure 4 Fluid pressure distribution at different time |
进一步观察流体在超声振动一个周期中的压力分布,由压力波峰开始,每隔τ/8取1个时刻,做出如图 5所示的研抛表面上的压力分布曲线.可以看出:整个流场的压力变化主要集中在以试件为中心直径约100 mm的范围内,最典型的变化呈现在研抛表面正下方.
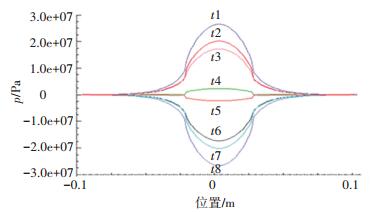
|
图 5 不同时刻流体压力的线分布 Figure 5 Pressure distribution curve of the polishing surface |
参照Sajjadi[14]的仿真模型设定方式,取流场初始气相体积分数为5%.在迭代计算收敛后,得到流场在一个周期各典型时刻的气相分布(如图 6).
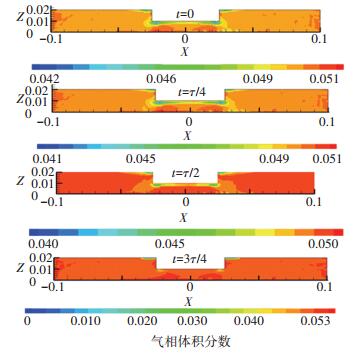
|
图 6 不同时刻流体气相分布 Figure 6 Fluid gas phase distribution at different time |
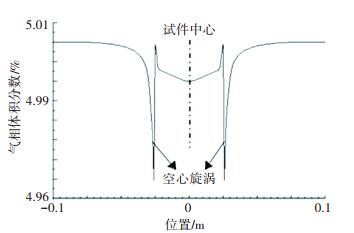
在τ/2时刻,研抛表面上流体的气相分布曲线见图 7.试件外部区域流场的气相体积分数稳定在5%,但在试件正下方,研抛表面附近流场气相体积分数明显低于其周围流体.特别是研抛表面边缘处流体中气相分布急剧下降,形成空心漩涡,一个周期内此处流体压力和速度反复交替变化,使气泡不断生长、溃灭、逸出,导致气相分布很不稳定.
|
图 7 液膜气相分布 Figure 7 Gas phase distribution of the polishing surface |
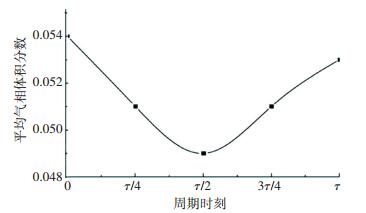
整个计算域中流体的平均气相体积分数在一个周期中的变化规律见图 8.由图 8可见,平均气相体积分数随时间的变化规律呈现为余弦曲线,在τ/2时刻达到最小值.但变化幅度不大.
|
图 8 流场气相平均体积分数变化 Figure 8 Average fluid gas volume fraction at different time |
研抛过程中研抛表面与抛光垫间的液膜厚度为40~100 μm, 其与整个计算域的直径相差很大,而流体特性在试件边缘以外的区域变化很小, 并且整体分布关于中线对称,因此取如图 9所示的一半流场作为实际研抛液膜流场物理模型.

|
图 9 实际研抛液膜模型 Figure 9 Thin film analysis model |
试件半径为25 mm,向外只取1 mm宽度,分别取液膜厚度h为40、60、100 μm进行仿真,其边界条件及网格划分除了在中线位置采用对称边界条件外,其他求解设置与厚膜作用模型相同.
2.2 速度分布不同膜厚下流体在τ/4时刻的速度流线图见图 10,可以看出试件外围流体流速变化较缓,试件下方的流体速度明显加快,试件边缘附近易形成涡流.

|
图 10 τ/4时刻不同液膜厚度下流体的流线图 Figure 10 Model streamline diagrams of different film thickness |
研抛表面横向速度分布见图 11. 40、60、100 μm膜厚下流体最大速度分别为180.0、61.3、22.5 m/s.由于入口纵向振动速度最大值为3.77 m/s,可见流体膜中流体速度主要是横向流动速度.液膜厚度越小,形成的剪切流速越高,有利于提高抛光效率.

|
图 11 不同膜厚下研抛表面流体横向速度分布 Figure 11 Fluid velocity distribution under different film thickness |
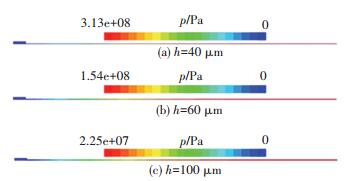
在设定的正弦速度入口振动条件下,3种不同液膜厚度对应在τ/2时刻的压力分布见图 12.试件表面不同径向位置处的压力分布见图 13.
|
图 12 不同膜厚液膜的压力云图 Figure 12 Pressure distribution in the film of different thickness |

|
图 13 不同膜厚下研抛表面的压力分布 Figure 13 Surface pressure distribution of different film thickness |
可以看出,3种膜厚模型的压力分布都呈现中间高、两头低的分布规律.膜厚越小,试件中心处压力越大,研抛表面的平均压力也越大.
2.4 气相分布3种膜厚下在τ/2时刻的气相分布见图 14.流体中的气泡在试件边缘以外最密集.结合流场速度分布规律可以发现,在试件向下挤压运动的过程中,研抛表面下液膜产生高速的横向流动,同时流体的压力快速升高,在液膜中不易形成气泡; 而在试件边缘之外,流场速度和压力数值迅速降低,形成涡流,易发生气泡凝聚.膜厚越小,剪切流越强,试件表面下液膜中的气体体积分数越少.

|
图 14 不同膜厚液膜中气相分布云图 Figure 14 Gas phase distribution in the film of different thickness |
进行电化学抛光时,考虑到试件与研抛盘之间需要导通电流,需要在介于试件和金属研抛盘之间的绝缘抛光垫上进行打孔,使研抛液连通试件与研抛盘.
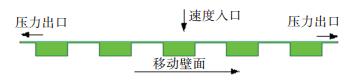
为探究小孔对研抛流场的影响,建立如图 15所示的多孔抛光垫与试件间流体的仿真模型.试件长20 mm,做纵向超声振动,其下表面和抛光垫上表面的初始液膜厚度为100 μm,抛光垫厚1 mm,小孔直径2 mm,间距2 mm,则试件下方对应有5个小孔.考虑到实际的研抛盘运动情况,设定粘结多孔抛光垫的铸铁研抛盘以1 m/s的速度向右运动.模型的网格划分与迭代设置与前述模型一致.
|
图 15 多孔抛光垫上流体仿真模型 Figure 15 Simulation model with poros polishing pad |
为方便观察流场的速度变化,按从左向右的顺序将抛光垫上的小孔编号.在1个周期的4个典型时刻,2号小孔内的研抛液流线图见图 16.可以看出,狭缝中的流体通过横向流动进入小孔并在孔内形成方向周期变化的涡流.当试件向下运动时,形成顺时针方向的涡流; 当试件向上运动时,形成逆时针方向的涡流.

|
图 16 试件下抛光垫2号孔内流体流线图 Figure 16 Fluid streamline diagram in hole No.2 at different moment |
τ/4时刻研抛试件表面上流体的横向剪切速度分布如17所示.由图 17可见,流体流经小孔上方对应的区域时,流体速度接近为0;在抛光垫的各个平台区域,剪切流速呈对称分布,两侧平台处的剪切速度高于中心附近平台处的,最高值约为20 m/s,且孔台交点对应位置流体速度有明显激增.
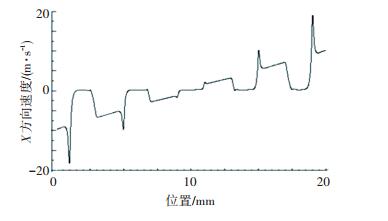
|
图 17 研抛表面上流体的横向速度分布 Figure 17 Fluid lateral velocity distribution on the polishing surface |
不同时刻的流体压力分布见图 18.由图 18可见,在同一周期中,多孔模型流场最大压力比无孔模型高出近100倍,达到2.09×109 Pa.与无孔模型结果相似,在任一时刻,流体压力的绝对值由中心向两侧降低; 关于中线对称的小孔中流体的压力分布并不完全对称,这表明小孔的存在影响了流场的层流状态,使小孔中的流体出现局部湍流,壁面的水平运动在一定程度上也干扰了各个小孔内的流体运动状态.
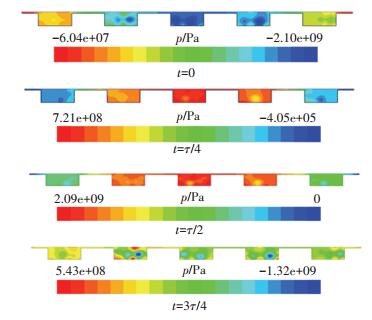
|
图 18 多孔抛光垫上液膜的压力云图 Figure 18 Pressure distribution of poros model |
气泡的聚集主要发生在压力较小的小孔区域.取2、3号小孔为例,作出4个典型时刻对应的两孔的气相分布如图 19所示.

|
图 19 多孔模型中气相分布 Figure 19 Gas phase distribution of poros model |
由图 19可见,在超声振动的影响下,小孔中流体所含的气泡先后经历了产生—膨胀—溃灭的过程.且气相的变化主要发生在小孔的内部区域,液膜间隙中的气相体积分数始终较小.一个周期中,小孔内的气相变化与压力变化相对应,在流体呈负压时,气泡产生聚集; 在流体呈正压时,气泡急剧溃灭.
整个计算域中流体的平均气相体积分数随时间的变化如图 20所示.对比图 8可知,其变化规律与平板厚膜超声作用下的规律一致,但多孔流体模型中的气相比例最高达26%,最低降至1%,即气相体积分数变化幅度远大于无孔模型时的, 表明抛光垫上开孔有利于流体中气泡的产生与凝聚,在正压作用下更多的气泡发生破裂,产生更强的气蚀作用,从而提高材料去除率.
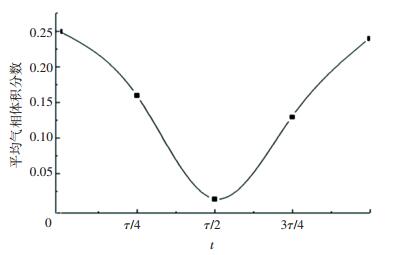
|
图 20 多孔模型平均气相体积分数变化 Figure 20 Average fluid gas volume fraction of poros model |
1) 超声振动使研抛表面上流体的平均速度、压力及流体气相体积分数都呈现正弦变化,当试件向下达到最低位置时,流场达到最大正压,而整个流场的平均气相体积分数最小.试件下方流体压力的绝对值由中心向两侧,逐渐降低至零; 横向剪切流速则是中间小两侧大; 在试件边缘容易形成空心漩涡.
2) 研抛工具与研抛表面之间的流体膜厚度越小,研抛液的速度与压力峰值越高,而液膜中的气相体积分数则随膜厚的减小而降低.因此,液膜厚度越小,研抛液对研抛表面的冲击与挤压作用越强,空化作用则相应减弱.
3) 与相同膜厚下无孔模型的仿真结果相比,抛光垫小孔使得试件表面的压力、流体速度绝对值以及气相体积分数的变化幅度大大增加,有利于抛光效率的提高.
4) 超声辅助有利于提高工件的材料去除率,控制液膜厚度在60~80μm,同时在抛光垫上加工出均匀排布的小孔,既可以提高研磨流体的冲击作用,又能促进超声空化现象的产生.
| [1] | KUMAR J, KHAMBA J S. Modeling the material removal rate in ultrasonic machining of titanium using dimensional analysis[J]. The International Journal of Advanced Manufacturing Technology, 2010, 481: 531-533. DOI: 10.1007/s00170-009-2287-1 |
| [2] | TSAI M, YANG W. Combined ultrasonic vibration and chemical mechanical polishing of copper substrates[J]. International Journal of Machine Tools & Manufacture, 2012, 53: 69-76. DOI: 10.1016/j.ijmachtools.2011.09.009 |
| [3] | LI Yaguo, WU Yongbo, ZHOU Libo, et al. Vibration-assisted dry polishing of fused silica using a fixed-abrasive polisher[J]. International Journal of Machine Tools & Manufacture, 2014, 77: 93-102. DOI: 10.1016/j.ijmachtools.2013.10.005 |
| [4] | LI Liang, HE Qing, ZHENG Mian, et al. Contribution of ultrasonic traveling wave to chemical-mechanical polishing[J]. Ultrasonics, 2015, 56: 530-538. DOI: 10.1016/j.ultras.2014.10.006 |
| [5] |
杨卫平. 超声椭圆振动—化学机械复合抛光硅片技术的基础研究[D]. 南京: 南京航空航天大学, 2008.
YANG Weiping. Research on the technology of ultrasonics assisted chemical mechanical polishing of silicon [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008. |
| [6] | PANDEY P M, MULIK R S. Ultrasonic assisted magnetic abrasive polishing of hardened AISI 52100 steel using unbounded SiC abrasives[J]. International Journal of Refractory Metals and Hard Materials, 2011, 29: 68-77. DOI: 10.1016/j.ijrmhm.2010.08.002 |
| [7] | ZHAO Qingliang, SUN Zhiyuan, GUO Bing. Material removal mechanism in ultrasonic vibration assisted polishing of micro cylindrical surface on SiC[J]. International Journal of Machine Tools & Manufacture, 2016, 103: 28-39. DOI: 10.1016/j.ijmachtools.2016.01.003 |
| [8] | XU Wenhu, LU Xinchu, PAN Guoshun, et al. Effects of the ultrasonic flexural vibration on the interaction between the abrasive Particles; Pad and sapphire substrate during chemical mechanical polishing (CMP)[J]. Applied Surface Science, 2011, 257(7): 2905-2911. DOI: 10.1016/j.apsusc.2010.10.088 |
| [9] | XU Wenhu, LU Xinchun, PAN Guoshun, et al. Ultrasonic flexural vibration assisted chemical mechanical polishing for sapphire substrate[J]. Applied Surface Science, 2010, 256(12): 3936-3940. DOI: 10.1016/j.apsusc.2010.01.053 |
| [10] | ALHEFI A, SUNDEN B A. A new formulation and analysis of a collapsing bubble with different content in a liquid induced during acoustic cavitation[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2016, 26(6): 1729-1746. DOI: 10.1108/HFF-02-2015-0044 |
| [11] |
李永春, 祝锡晶, 郭策, 等. 超声珩磨区实际气体的单空泡动力学分析[J].
应用声学, 2014(6): 528-533.
LI Yongchun, ZHU Xijing, GUO Ce, et al. Research on the gas dynamics in the single cavity area during ultrasonic honing[J]. Application of acoustic, 2014(6): 528-533. |
| [12] |
郭策, 祝锡晶, 刘国东, 等. 基于功率超声珩磨的空化泡动力学模型的研究[J].
组合机床与自动化加工技术, 2012(6): 42-44.
GUO Ce, ZHU Xijing, LIU Guodong, et al. Research on the dynamic model of the cavitation bubble based on ultrasonic honing[J]. Combination machine tools and automatic processing technology, 2012(6): 42-44. |
| [13] |
孙冰, 张会臣. 基于CFD方法的超声空化发生特性数值分析[J].
润滑与密封, 2009(4): 55-60.
SUN Bing, ZHANG Huichen. Numerical analysis of the ultrasonic cavitation characteristics based on CFD method[J]. Lubrication and Sealing, 2009(4): 55-60. |
| [14] | SAJJADI B, RAMAN A A, IBRAHIM S. Influence of ultrasound power on acoustic streaming and micro-bubbles formations in a low frequency sono-reactor: Mathematical and 3D computational simulation[J]. Ultrasonics Sonochemistry, 2015, 24: 193-203. DOI: 10.1016/j.ultsonch.2014.11.0131350-4177 |
| [15] | SKOCZYPIEC S. Research on ultrasonically assisted electrochemical machining process[J]. Int J Adv Manuf Technol, 2011, 52: 565-574. DOI: 10.1007/s00170-010-2774-4 |
 2017, Vol. 49
2017, Vol. 49


