在工程领域, 特别是航空航天以及国防领域,对执行机构或者新开发的伺服系统进行带载测试,验证产品的质量和性能至关重要[1].加载系统,又称为负载模拟系统,是执行机构或者伺服驱动系统研制与测试过程中的重要设备,能够在实验室环境下复现载荷谱[2],为产品性能测试提供相应的负载环境。这种方法能够显著改善实验质量,降低研发成本,加快产品研发进度[3-4].加载系统可以再现伺服系统在真实环境中受到的负载力矩,为发现所研发设备或系统潜在的问题以及研究各种控制算法提供了方便的手段[5].加载系统的加载性能直接决定了测试结果的准确性[6],所以需要加载系统能够精确地、重复地复现载荷谱.
按照驱动形式,负载模拟系统主要包括以下几种[7]:机械负载模拟器、电动负载模拟器、电液负载模拟器、气动负载模拟器[8].其中电动负载模拟器和电液负载模拟器具有能够模拟任意载荷谱,且精确、快速等优点,被广泛应用于机器人、自动化工业、汽车、航空航天等领域.但是,这两种加载系统存在着一直难以解决的问题[9-10]:在加载过程中负载模拟器受到被测试设备运动的干扰,致使其动态加载性能受到影响; 当被测试设备运动剧烈时,加载系统有时很难复现所要求的载荷谱.如何消除负载模拟器加载时所受到的运动干扰是研究负载模拟领域的关键问题[11-13],大量的研究试图从机械结构和控制补偿两方面消除或者减小这种干扰.结构补偿,主要是通过增加机械、液压等缓冲装置[14-15]或者是利用辅助同步系统使加载设备和被加载设备同步[16],以减小多余力矩; 控制补偿方面,主要是通过各种方法估计干扰并反馈补偿[17-18],或者利用具有强鲁棒性和自适应性的控制策略抑制干扰[19-20].有时被测试设备运动剧烈时,干扰也会很大很剧烈,会超出了控制补偿范围; 而结构方法只能起到一定的效果,并且由于费用昂贵和安装精度高等原因,实际工程应用非常困难.
负载模拟器有很多关键性问题亟待解决:负载模拟器受到被测试物体运动干扰,严重影响系统的加载性能,难以保证小力矩加载性能和高精度的动态加载; 真实负载变化多样,变化剧烈,传统负载模拟器的带宽很难满足要求; 为提高传统负载模拟器性能,其控制策略复杂,控制策略通用性较差.消除这些弊端的有效途径是改变这种直接拖拉加载方案,寻找新的设备和技术去提高动态加载性能和加载带宽,实现精确的负载模拟.
本文详细介绍了传统电液负载模拟器存在的问题; 然后, 提出摩擦加载系统的方案,推导其理论数学模型,并且基于数学模型分析了其加载特性和各种参数变化对系统性能的影响; 最后,通过仿真验证了摩擦加载方案的可行性及加载性能.
1 传统电液负载模拟器问题分析传统电液负载模拟器一般由加载系统和被测试系统两大部分组成.通常被测试系统为位置伺服系统,而加载系统是力矩伺服系统,加载系统与被测试设备连接,利用连接轴变形产生扭矩进行加载.
根据文献[21],可得传统电液负载模拟器的数学模型如下:
| $ \begin{array}{*{20}{c}} {T\left( s \right) = \left[ {A\left( s \right){x_v}\left( s \right) - B\left( s \right) \cdot s \cdot {\theta _{\rm{a}}}\left( s \right)} \right]/C\left( s \right),} \end{array} $ | (1) |
| $ \begin{array}{*{20}{c}} {A\left( s \right) = {K_q}{D_1},}\\ {B\left( s \right) = \frac{{{J_1}V}}{{4{\beta _{\rm{e}}}}}{s^2} + \left( {{J_1}{C_{\rm{t}}} + \frac{{{B_1}V}}{{4{\beta _{\rm{e}}}}}} \right)s + {B_1}{C_{\rm{t}}} + D_1^2,}\\ {C\left( s \right) = \frac{{{J_1}V}}{{4{\beta _{\rm{e}}}{G_s}}}{s^3} + \left( {\frac{{{B_1}V}}{{4{\beta _{\rm{e}}}{G_{\rm{s}}}}} + \frac{{{J_1}{G_{\rm{t}}}}}{{{G_{\rm{s}}}}}} \right){s^2} + }\\ {\left( {\frac{{{B_1}{C_{\rm{t}}} + D_1^2}}{{{G_{\rm{s}}}}} + \frac{V}{{4{\beta _{\rm{e}}}}}} \right)s + {C_{\rm{t}}}.} \end{array} $ |
式中:s是Laplace算子,T为力矩输出(N·m),θa是被测试马达输出转角(rad),Kq为伺服阀空载流量增益(m2/s),D1为液压马达排量(m3/rad),J1为负载转动惯量(kg·m2),V为加载马达等效控制容积(m3),βe是油液等效体积弹性模量(N/m2), Ct为泄漏系数(m5/(N·s)), B1为阻尼系数(N·m/(rad·s-1)), Gs为连接轴的等效扭转刚度(N·m/rad).
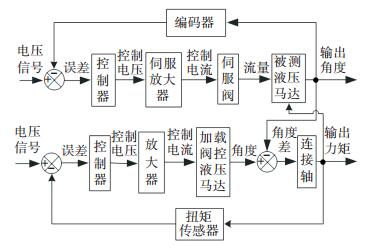
由式(1) 可以看出,传统电液负载模拟器输出力矩由两部分构成,第一部分是被期望的模拟负载的力矩,第二部分是被测试马达运动带来的干扰力矩.而且这种干扰力矩具有被测试马达速度、加速度以及加加速的的量纲,换言之,这种干扰力矩与被测试马达运动状态关系密切. 图 1为系统加载原理方框图,能更清晰地表达两者之间的关系.被测试设备主动运动时,由于加载系统与被测试系统通过连接轴连接在一起,所以加载系统在被测试系统的强制拖动下一起转动,这就要求加载系统在跟踪力矩信号的同时完全同步被测试系统; 但是加载系统只输入力矩信号而并未输入跟踪被测试系统的位置信号,被测试设备运动势必造成与负载模拟器之间产生位移差,通过连接轴作用于加载系统,对加载系统来说是一种强干扰.
|
图 1 传统电液负载模拟器原理框图 Figure 1 Principle block diagram of conventional electro-hydraulic load simulator |
改变被测试马达运动状态,仿真测试加载性能,仿真所用参数见表 1.
| 表 1 摩擦电液加载系统仿真参数 Table 1 Simulation parameters |
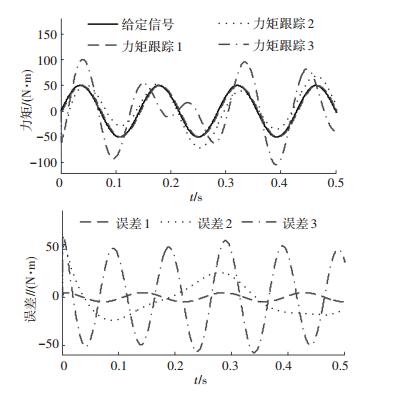
给定摩擦电液加载系统幅值为50 N·m、频率为7 Hz的正弦力矩指令信号,调定PI控制器参数,比例系数为1.3,积分系数为68,仿真结果如图 2所示.
|
图 2 传统电液负载模拟器力矩仿真 Figure 2 Torque simulation of conventional electro-hydraulic load simulator |
图 2中力矩跟踪1、2、3分别表示被测试马达不运动,以幅值3°、频率3 Hz正弦运动,以幅值1°、频率10 Hz正弦运动时,传统电液负载模拟器力矩跟踪曲线,误差1、2、3分别表示相应的力矩跟踪误差.从图 2中可以看出,被测试马达不运动时,力矩误差在±5 N·m以内; 而被测试马达以幅值3°、频率3 Hz正弦运动,以幅值1°、频率10 Hz正弦运动时,力矩误差分别在±22 N·m和±60 N·m范围内.很显然,当被测试马达运动时,力矩误差增大了一个数量级,可见被测试马达运动对传统电液负载模拟器加载性能影响很大.
由模型分析和仿真可知,传统电液负载模拟器利用弹性变形产生的弹性力模拟负载力矩,方法简单、操作方便,但是由于被测试物体会任意运动,不可避免对加载系统引起干扰力矩.这种干扰力矩随着被测试马达运动状态的改变而改变,有时会比较大,严重影响加载性能的进一步提升.
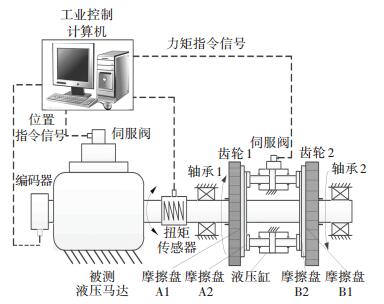
2 摩擦电液伺服加载系统 2.1 摩擦电液伺服加载系统原理除了利用弹性体变形产生力外,还有许多产生力或力矩的方法,例如载流导体在磁场中会受到电磁力,两个相互接触物体相对运动会产生摩擦力等,这些都可以用于负载模拟.利用摩擦力原理进行力传递已经应用于许多设备中,包括摩擦离合器、摩擦制动器、摩擦道奇软启动装置.在一定条件下,摩擦传动可以不改变两相对运动物体的运动状态而传递力或者力矩,这一点对负载模拟系统是十分重要的.应用摩擦原理模拟负载,提出了摩擦加载方案,如图 3所示.
|
图 3 摩擦电液加载系统原理 Figure 3 Principle schematic of friction electro-hydraulic loading system |
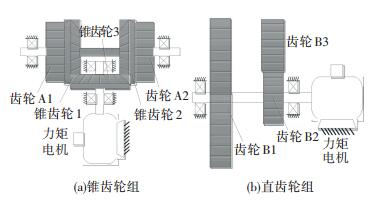
图 3中左侧为承载马达,实现模拟舵机运动; 右侧为加载系统,实现力矩正反向输出.加载系统主要包括一套阀控双出杆液压缸伺服系统、两套摩擦装置、双向运动系统.其中摩擦装置通过主从动摩擦片相对旋转,实现从动摩擦片的摩擦力矩输出作用于被测试系统的输出轴.为了产生两个方向的相对运动,可采用图 4(a)中的锥齿轮组或者图 4(b)中的直齿轮组两种结构实现.双向运动系统由两套齿轮组分别带动左右两套摩擦装置中的主动摩擦片正反向旋转,这样在两套摩擦装置中主从动摩擦片之间的相对旋转方向相反.根据摩擦力与运动方向相反的原理可知,两套摩擦装置从动摩擦片输出的摩擦力矩相反,因此可以实现双向力矩输出.通过控制阀控液压缸伺服系统液压缸伸缩,分别压紧和释放两套摩擦装置中主从动摩擦片,实现主从动摩擦片之间压力连续变化,进而控制摩擦力矩的连续变化.安装在轴上的力矩传感器采集力矩信号,控制器根据给定信号得出控制信号,实现力矩闭环控制系统,精确地控制产生的摩擦力矩,完成被测试系统的带载测试.摩擦加载系统不同于通过弹性变形产生弹性力的加载系统,这种方法可以有效避免被测试系统运动对加载系统的影响.
|
图 4 摩擦加载系统换向机构 Figure 4 Reverse mechanism of friction loading system |
摩擦加载系统主要利用两相互接触的摩擦盘相对转动产生摩擦力矩来模拟舵机所受的加载力矩,考虑摩擦力为理想库伦摩擦,主从动摩擦片之间的接触为环面接触,可得摩擦力矩表达式.
| $ T = \int_{{R_1}}^{{R_2}} {\mu pr{\rm{d}}A} = \mu RF. $ |
式中:μ为摩擦因数,p为摩擦副接触区域正压力(Pa),R1为摩擦副接触区域内径(m),R2为摩擦副接触区域外径(m),A为摩擦副接触区域面积(m2),F为摩擦面上载荷(N),R为摩擦等效半径(m), 且
| $ R = \frac{2}{3}\mu \frac{{R_2^3 - R_1^3}}{{R_2^2 - R_1^2}}. $ |
作用在摩擦副上的载荷为
| $ F = K{y_{\rm{c}}}. $ |
摩擦负载模拟器中,液压动力元件是一个关键性的部件,其动态性能对整个系统的性能起着重要作用.所以要分析摩擦负载模拟器,就必须建立系统中的阀控液压缸的传递函数.阀控液压缸的动态特性一般可以用下列3个基本方程来表示.
1) 伺服阀的流量方程.
| $ {Q_{{\rm{cL}}}} = {C_{\rm{d}}}w{x_{{\rm{cv}}}}\sqrt {\frac{1}{\rho }\left( {{p_{\rm{s}}} - {\rm{sign}}\left( {{x_{{\rm{cv}}}}} \right){p_{{\rm{cL}}}}} \right)} . $ | (2) |
式中:QcL为伺服阀负载流量(m3/s),Cd为伺服阀阀口流量系数,w为伺服阀节流口面积梯度(m),xcv为伺服阀阀芯位移(m),ρ为液压油密度(kg/m3),ps为供油压力(Pa),pcL为负载压力(Pa),sign(·)为符号函数.
定义负载流量和负载压力分别为
| $ \begin{array}{*{20}{c}} {{Q_{{\rm{cL}}}} = \left( {{Q_1} + {Q_2}} \right)/2,}\\ {{p_{{\rm{cL}}}} = {p_1} - {p_2}.} \end{array} $ | (3) |
式中:Q1为液压缸流入流量(m3/s),Q2为液压缸流出流量(m3/s),p1为液压缸进油腔压力(Pa),p2为液压缸出油腔压力(Pa).
将式(2) 在工作点处线性化
| $ {Q_{{\rm{cL}}}} = {K_{\rm{q}}}{x_{{\rm{cv}}}} + {K_{\rm{c}}}{p_{{\rm{cL}}}}. $ |
式中:Kq为伺服阀流量增益系数(m2/s),Kc为伺服阀流量压力系数((m3·s-1)/Pa).
2) 液压缸流量连续性方程.
流入液压缸进油腔的流量为
| $ {Q_1} = {A_{\rm{p}}}{{\dot y}_{\rm{c}}} + \frac{{{V_1}}}{{{\beta _{\rm{e}}}}}{{\dot p}_1} + {C_{{\rm{ip}}}}\left( {{p_1} - {p_2}} \right) + {C_{{\rm{ep}}}}{p_1}, $ | (4) |
| $ {Q_2} = {A_{\rm{p}}}{{\dot y}_{\rm{c}}} + \frac{{{V_2}}}{{{\beta _{\rm{e}}}}}{{\dot p}_2} + {C_{{\rm{ip}}}}\left( {{p_1} - {p_2}} \right) - {C_{{\rm{ep}}}}{p_2}. $ | (5) |
式中:Ap为液压缸活塞有效面积(m2),yc为液压缸活塞位移(m),V1为液压缸进油腔有效容积(m3),V2为液压缸出油腔有效容积(m3),Cip为液压缸内泄漏系数((m3·s-1)/Pa),Cep为液压缸外泄漏系数((m3·s-1)/Pa).
假设阀是对称且匹配的,由油路原理图可知
| $ {p_{\rm{s}}} = {p_1} + {p_2}, $ | (6) |
定义总有效压缩容积为
| $ {V_{{\rm{ct}}}} = {V_1} + {V_2}. $ | (7) |
结合式(3)~式(6) 可得液压缸负载流量连续方程为
| $ {Q_{{\rm{cL}}}} = {A_{\rm{p}}}{{\dot y}_{\rm{c}}} + {C_{{\rm{tp}}}}{p_{{\rm{cL}}}} + \frac{{{V_{{\rm{ct}}}}}}{{4{\beta _{\rm{e}}}}}{{\dot p}_{{\rm{cL}}}}. $ |
式中Ctp为液压缸总泄漏系数((m3·s-1)/Pa),且Ctp=Cip+Cep/2.
3) 负载力平衡方程.
液压动力元件的动态特性与负载特性密切相关,在本系统中,液压缸推动摩擦副相互挤压,负载力主要包括惯性力、黏性阻尼力、弹性力以及摩擦力,由牛顿第二定律可得
| $ {A_{\rm{p}}}{p_{{\rm{cL}}}} = {m_{\rm{c}}}{{\ddot y}_{\rm{c}}} + {B_{\rm{c}}}{{\dot y}_{\rm{c}}} + K{y_{\rm{c}}} + f. $ |
式中:mc为负载折算到活塞上的质量(kg),Bc为黏性阻尼系数(N·s/m),K为负载弹簧刚度(N/m),f为负载运动摩擦力(N).
一般伺服阀输入电流与阀芯位移之间可以近似表示为
| $ {{\ddot x}_{{\rm{cv}}}} = 2{\zeta _{{\rm{sv}}}}{\omega _{{\rm{sv}}}}{{\dot x}_{{\rm{cv}}}} + \omega _{{\rm{sv}}}^2{x_{{\rm{cv}}}} = {K_{{\rm{sv}}}}\omega _{{\rm{sv}}}^2{i_{\rm{c}}}. $ |
相对系统中的机械和液压环节, 电气环节的带宽高很多.所以,在本课题研究范围内,可以不考虑纯电气环节的动态特性,直接将纯电气环节近似为比例环节.这样,输入控制电压与伺服阀输入电流之间的关系式可以写成uc=Kaic.忽略摩擦力,结合上述所有公式Laplace变换,整理可得输出力矩的表达式如下:
| $ {T_{\rm{c}}}\left( s \right) = \frac{2}{3}\frac{\mu }{{{A_{\rm{p}}}}}\frac{{K{K_{\rm{a}}}{G_{{\rm{sv}}}}\left( s \right)}}{{{G_{\rm{c}}}\left( s \right)}}\frac{{R_2^3 - R_1^3}}{{R_2^2 - R_1^2}}{u_{\rm{c}}}. $ | (8) |
式中:Ka为伺服放大器增益(A/V),Kce为总流量压力系数((m3·s-1)/Pa),
| $ \begin{array}{*{20}{c}} {{G_{{\rm{sv}}}}\left( s \right) = \frac{{{K_{{\rm{sv}}}}\omega _{{\rm{sv}}}^2}}{{{{\rm{s}}^2} + 2{\xi _{{\rm{sv}}}}{\omega _{{\rm{sv}}}}s + \omega _{{\rm{sv}}}^2}},}\\ {{K_{{\rm{ce}}}} = {C_{{\rm{tp}}}} + {K_{\rm{c}}},} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{G_{\rm{c}}}\left( s \right) = \frac{{{V_{{\rm{ct}}}}{m_{\rm{c}}}}}{{4{\beta _{\rm{e}}}A_{\rm{p}}^2}}{s^3} + \left( {\frac{{{m_{\rm{c}}}{K_{{\rm{ce}}}}}}{{A_{\rm{p}}^2}} + \frac{{{V_{{\rm{ct}}}}{B_{\rm{c}}}}}{{4{\beta _{\rm{e}}}A_{\rm{p}}^2}}} \right){s^2} + }\\ {\left( {\frac{{K{V_{{\rm{ct}}}}}}{{4{\beta _{\rm{e}}}A_{\rm{p}}^2}} + \frac{{{B_{\rm{c}}}{K_{{\rm{ce}}}}}}{{A_{\rm{p}}^2}} + 1} \right)s + \frac{{K{K_{{\rm{ce}}}}}}{{A_{\rm{p}}^2}}.} \end{array} $ |
式(8) 中不含有被测试对象的参数,可以看出, 摩擦负载模拟器输出力矩与被测试物体的结构参数和运动状态无直接关系.经典摩擦定律认为摩擦力与载荷成正比,静摩擦因数大于动摩擦因数,并且摩擦因数与表观接触面积以及滑动速度无关.虽然经典摩擦定律并不完全正确,但是它还是在一定程度上反映了滑动摩擦机理,并且工程实际问题中它可以很大程度上近似描述真实的摩擦力.假设理想情况下,摩擦因数如经典摩擦定律描述的与滑动速度等无关,就可以认为摩擦负载模拟器不受被测试物体运动的影响.
然而,实际过程中摩擦力十分复杂,并不能用单一的模型或者定律完全描述摩擦现象.摩擦因数是衡量摩擦ζ副系统综合特性的关键因素,受到滑动过程中各种因素的影响,如相对滑动速度、温度和法向载荷大小等.所以可以将摩擦因数写成
| $ \mu \left( {F,\dot \theta ,T} \right) = \mu + \Delta \mu \left( {F,\dot \theta ,T} \right). $ |
式中:μ(F, $\dot \theta$, T)、Δμ(F, $\dot \theta$, T)、μ分别为摩擦因数实际值、变化量和理论值.
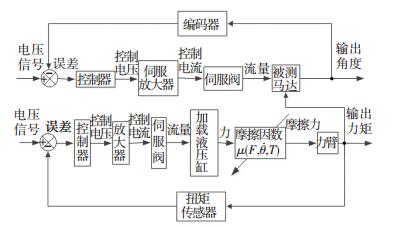
为使加载系统随时都能摩擦产生加载力矩,加载系统与被测试系统在整个加载测试过程中必须有相对转动,摩擦产生摩擦力矩过程中,摩擦生热使摩擦副温度升高,会使摩擦因数随温度发生改变,同时摩擦因数还会随着两个系统相对运动状态改变而发生变化. 图 5为摩擦加载系统在摩擦因数随相对滑动速度变化情况下的加载原理.对比图 1、图 5表明,被测试系统运动状态会使加载系统参数发生变化,而且加载系统本身的加载力也会改变摩擦因数的大小,这些因素都会影响加载性能.因此,被测试系统运动,对于传统电液负载模拟器来说是一种外干扰,而对于摩擦负载模拟器来说是一种参数摄动.
|
图 5 摩擦加载系统原理方框图 Figure 5 Principle block diagram of friction loading system |
为了验证所提加载方案的有效性,仿真摩擦电液加载系统不同摩擦因数变化时的加载性能.仿真参数见表 1.
在摩擦电液加载系统中,相比其他系统参数,摩擦因数是最不确定的、最易变的,也是最关键的参数.因此在仿真过程中,主要考虑摩擦因数变化引起的系统性能变化,而忽略其他因素的影响.由于摩擦因数随相对滑动速度、温度、载荷等变化,不容易表达,所以不考虑这些影响因素的具体影响规律,只考虑极限情况,即摩擦因数在极限范围不断变化对摩擦加载系统加载性能的影响.
定义系统开环增益为
| $ {K_{\rm{G}}} = \frac{2}{3}\frac{\mu }{{{A_{\rm{p}}}}}\frac{{R_2^3 - R_1^3}}{{R_2^2 - R_1^2}}{K_{\rm{a}}}{K_{{\rm{sv}}}}\omega _{{\rm{sv}}}^2. $ | (9) |
从式(9) 可以看出,其他条件不变的情况下,摩擦因数越小,系统开环增益变小,摩擦加载控制系统幅值裕量越大; 而摩擦因数越大,系统开环增益变大,摩擦加载控制系统幅值裕量就越小,当摩擦因数超过一定范围时,此系统变得不稳定.
在大范围来看,摩擦随着各个因素的变化有一个缓慢的变化趋势.在小范围来看,摩擦因数不断快速地发生微小变化.用不同频率正弦信号和随机信号来表示摩擦因数的变化,低频正弦表示摩擦因数发生缓慢或大或小的变化,高频正弦和高频随机信号表示摩擦因数实时发生变化.给定摩擦电液加载系统幅值为50 N·m、频率为7 Hz的正弦力矩指令信号,调定PI控制器参数,比例系数为12,积分系数为31.5,仿真结果如图 6所示.
|
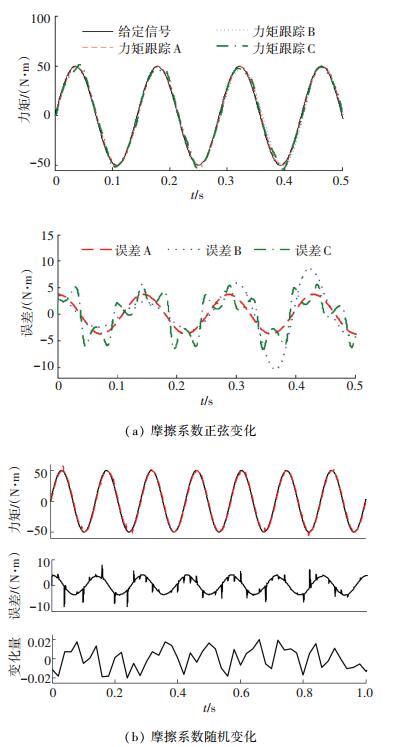
图 6 摩擦系数变化时的力矩跟踪仿真 Figure 6 Torque tracking with variable friction coefficient |
图 6(a)中力矩跟踪A、B、C分别表示摩擦因数不变、以幅值0.12频率、2 Hz变化,幅值0.06、频率20 Hz变化时的力矩跟踪曲线,误差A、B、C分别是相应的力矩跟踪误差曲线.由图 6(a)可以看出,随着摩擦因数不同变化,力矩跟踪误差大约都在±5 N·m范围内; 而且随着摩擦因数变化幅值的增大和频率的增高,力矩跟踪误差变大,力矩波动变剧烈,跟踪性能变坏. 图 6(a)中力矩跟踪误差曲线B的误差范围初始时比误差曲线A的小,而后却比误差曲线A大,结合对公式(17) 的分析可知:这是由于摩擦因数先逐渐增大,系统控制量变大,系统响应快,跟踪误差小; 而后来摩擦因数逐渐减小,系统控制量变小,进而使得力矩输出跟踪不上,跟踪误差变大. 图 6(b)是摩擦因数以幅值0.02、频率50 Hz的随机信号变化时力矩跟踪曲线和力矩跟踪误差曲线.误差范围大约在±5 N·m内,而且在一些时刻曲线会有“尖峰”,这是由于这种随机变化相对正弦变化更为剧烈,所以在摩擦因数突变比较大的时刻,会突然出现较大的误差,这就是前文所述的“尖峰”,例如在0.8 s左右摩擦因数变化量从-0.018跳跃到+0.018,这时误差达到-8 N·m.
上述仿真,摩擦因数变化已经远远超出平常状态下摩擦因数变化范围.仿真结果表明,摩擦因数幅值变化大,会使力矩跟踪误差变大; 摩擦因数变化频率越高,会使力矩跟踪波动变剧烈,对加载性能的影响就会比较大; 然而只要摩擦因数在一定的范围内(2 Hz幅值变化60%,20 Hz幅值变10%)变化,摩擦加载系统依然具有良好的加载性能.
综上可以看出,被测试马达运动会对传统电液负载模拟器加载部分产生强干扰,力矩跟踪效果变差,甚至不能跟踪给定力矩.而被测试马达运动、温度、载荷等因素引起摩擦因数发生比较大的变化时,摩擦电液加载系统力矩跟踪误差范围也不会发生很大的变化.
4 结论1) 在被测试马达运动时,传统电液负载模拟器受被测试马达运动干扰,力矩跟踪性能严重变差.本文提出了一种新型摩擦电液加载系统,它应用摩擦传动原理实现力矩负载模拟,通过分析其数学模型,初步验证这种摩擦加载系统理论上可以不受被测试对象运动的影响.
2) 考虑实际情况,在摩擦电液伺服加载系统工作过程中,由于受相对滑动速度、温度和压力等因素的影响,摩擦因数在一定范围内变化.摩擦因数相对其他参数,其不确定性和非线性更为严重,相对变化量也比较大.这对于摩擦电液伺服加载系统,是一种参数摄动,影响加载性能.
3) 摩擦因数对摩擦电液加载系统控制性能的影响:一方面,摩擦因数变小会使摩擦电液伺服加载控制系统控制量变小,进而使得力矩输出跟踪不上; 摩擦因数变大会使系统控制量变大,进而系统响应更快,超调更大,跟踪误差更小.另一方面,摩擦因数变化越快,使得系统输出力矩波动也就越剧烈.
4) 摩擦电液加载系统中摩擦因数虽然受被测试马达运动影响,但这种影响相对传统电液负载模拟器强位置干扰则比较小.通过仿真分析摩擦因数变化对摩擦电液加载系统的影响,验证了摩擦系数在一定范围内变化时,摩擦电液加载系统仍然能够具有较好的力矩跟踪性能.在后续研究过程中,应该采用合适的控制器提高加载性能.
| [1] | YALLA S K, KAREEM A, ASCE M. Dynamic load simulator: Actuation strategies and applications[J]. Journal of Engineering Mechanics, 2007, 133(8): 855-863. DOI: 10.1061/(ASCE)0733-9399(2007)133:8(855) |
| [2] |
张彪. 电液负载模拟器多余力矩抑制及其反步自适应控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2009.
ZHANG B. Extra torque rejection and adaptive backstepping control of electro hydraulic load simulator [D]. Harbin: Harbin Institute of Technology, 2009. |
| [3] | ISERMANN R, SCHAFFNIT J, SINSEL S, et al. Hardware-in-the-loop simulation for the design and testing of engine control systems[J]. Control Engineering Practice, 1999, 7(5): 643-653. DOI: 10.1016/S0967-0661(98)00205-6 |
| [4] | RADPUKDEE T, JIRAWATTANA P. Design of an engine load simulator[C]// 2005 ASME International Mechanical Engineering Congress and Exposition, IMECE2005. New York: American Society of Mechanical Engineers, 2005:17-25. DOI:10.1115/IMECE2005-80126. |
| [5] | WANG Chengwen, JIAO Zongxia, WU Shuai, et al. An experimental study of the dual-loop control of electro-hydraulic load simulator (EHLS)[J]. Chinese Journal of Aeronautics, 2013, 26(6): 1586-1595. DOI: 10.1016/j.cja.2013.10.002 |
| [6] |
韩松杉, 焦宗夏, 尚耀星, 等. 基于舵机指令前馈的电液负载模拟器同步控制[J].
北京航空航天大学学报, 2015, 41(1): 124-132.
HAN Songshan, JIAO Zongxia, SHANG Yaoxing, et al. Synchronizing compensation control of electro-hydraulic load simulator using command signal of actuator[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(1): 124-132. DOI: 10.13700/j.bh.1001-5965.2014.0052 |
| [7] | WANG Shoukun, WANG Junzheng. A new kind of hydraulic proportional loading method for actuator testing based on the relief valve controlled cylinder[J]. Transactions of the Institute of Measurement & Control, 2013, 35(35): 157-165. DOI: 10.1177/0142331211434658 |
| [8] |
冯世泽. 基于动压反馈的气动负载模拟器控制策略研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.
FENG Shize.Research on the control strategies of pneumatic loader simulator based on dynamic pressure feedback[D]. Harbin: Harbin Institute of Technology, 2012. |
| [9] | LI Jianying, WANG Yanwei, WANG Xiaojing, et al. Research on control strategy of passive force load electro-hydraulic servo system[J]. Journal of Computational and Theoretical Nanoscience, 2015, 12(9): 2084-8090. DOI: 10.1166/jctn.2015.3989 |
| [10] | WANG Xingjian, WANG Shaoping. High performance torque controller design for electric load simulator[C]// Proceedings of the 2011 6th IEEE Conference on Industrial Electronics and Applications, ICIEA 2011. Washington: IEEE Computer Society, 2011:2499 -2505. DOI:10.1109/ICIEA.2011.5976013. |
| [11] | WANG Chengwen, JIAO Zongxia, WU Shuai, et al. Nonlinear adaptive torque control of electro-hydraulic load system with external active motion disturbance[J]. Mechatronics, 2014, 24(1): 32-40. DOI: 10.1016/j.mechatronics.2013.11.005 |
| [12] | WANG Hongyan, LU Jinbo, DAI Xing, et al. Modeling and dynamic research of the pneumatic-hydraulic loading simulator system[M]. Zurich: Trans Tech Publications Inc, 2014: 8-12. |
| [13] | WANG Xiaohua, WU Shuai, JIAO Zongxia. RBF-elman neural network control on electro-hydraulic load simulator[J]. Applied Mechanics & Materials, 2013, 433-435: 1054-1060. DOI: 10.4028/www.scientific.net/AMM.433-425.1054 |
| [14] |
王经甫, 叶正茂, 李洪人. 双阀并联控制在船舶舵机电液负载模拟器多余力抑制中的研究[J].
机械工程学报, 2005, 41(4): 229-234.
WANG Jingfu, YE Zhengmao, LI Hongren.. Study on eliminating the superfluous force of marine electro-hydraulic load simulator applied with dual-valve parallel connected control[J][J]. Chinese Journal of Mechanical Engineering, 2005, 41(4): 229-234. DOI: 10.3901/JME.2005.04.229 |
| [15] | SHAO Junpeng, LI Jianying, WANG Zhongwen, et al. Research on electro-hydraulic load simulator based on building model of flow press servo valve[J]. Advanced Materials Research, 2010, 129-131: 213-217. DOI: 10.4028/www.scientific.net/AMR.129-131.213 |
| [16] | YU Ciyuan, LIU Qinghe, ZHAO Keding. Velocity feedback in load simulator with a motor synchronizing in position[J]. Journal of Harbin Institute of Technology, 1998(3): 78-81. |
| [17] |
李运华, 焦宗夏, 王占林. 舵机力矩负载模拟器的混合控制方法研究[J].
航空学报, 1998, 19(S1): 61-65.
LI Yunhua, JIAO Zongxia, WANG Zhanlin. Research on hybrid control method of momental load simulator of actuator[J]. Acta Aeronautica et Astronautica Sinica, 1998, 19(S1): 61-65. |
| [18] | JIAO Zongxia, GAO Junxia, HUA Qing, et al. The velocity synchronizing control on the electro-hydraulic load simulator[J]. Chinese Journal of Aeronautics, 2004, 17(1): 39-46. DOI: 10.1016/S1000-9361(11)60201-X |
| [19] | WANG Chengwen, JIAO Zongxia, WU Shuai, et al. A practical nonlinear robust control approach of electro-hydraulic load simulator[J]. Chinese Journal of Aeronautics, 2014, 27(3): 735-744. DOI: 10.1016/j.cja.2014.04.011 |
| [20] | YAO Jianyong, JIAO Zongxia, YAO Bin. Nonlinear adaptive robust backstepping force control of hydraulic load simulator: Theory and experiments[J]. Journal of Mechanical Science and Technology, 2014, 28(4): 1499-1507. DOI: 10.1007/S12206-014-0137-2 |
| [21] | WANG Chengwen, JIAO Zongxia, QUAN Long. Adaptive velocity synchronization compound control of electro-hydraulic load simulator[J]. Aerospace Science & Technology, 2015, 42(9): 309-321. DOI: 10.1016/j.ast.2015.01.018 |
 2017, Vol. 49
2017, Vol. 49


