2. 车辆传动国防科技重点实验室(北京理工大学),北京 100072
2. Key Laboratory of National Defense Science and Technology of Vehicle Transmission(Beijing Institute of Technology), Beijing 100072, China
传统电液比例阀一般采用比例电磁铁作为电-机械转换元件.比例电磁铁输出力与其控制电流成比例,该电磁力作用在阀芯上,与作用在阀芯另一端的反馈压力比对,动态调整并达到平衡.平衡时反馈压力主要由电磁力决定,从而实现比例压力阀功能[1-3].由于压电作动器优良的特性[4],在液压技术中也获得了越来越多的应用,如何秀华[5]、黄俊[6]等应用压电作动器研制了压电泵.许多研究者利用压电作动器进行了液压伺服阀和比例阀的研究. Lindler等[7]利用积层式压电作动器直接驱动阀芯,并采用杠杆式位移放大机构对输出位移进行放大,阀芯位移可达300 μm,但动态特性不理想; Bauer等[8]利用压电堆驱动位移放大机构,直接驱动滑阀阀芯,取得了1 050 Hz的高频响,阀的压力3.5 MPa,流量9 L/min; 亚琛大学的Reichert等[9]研制了一种压电驱动伺服阀,在主阀芯的两端分别用两只压电堆驱动两个锥阀,这两个锥阀一个控制进油,另一个控制排油,从而控制主阀芯运动; 许有熊等[10]利用压电驱动两只高速开关阀控制先导腔压力,测量主阀出口压力构成闭环控制,实现了基于压电驱动的高速PWM气动压力比例阀.鄂世举等[11]用压电元件做驱动器,利用位移传感器进行位置信号反馈,与压电驱动器构成一个闭环位置系统,提高阀的动静态特性.哈尔滨工业大学郭向东[12]以压电弯振片作为挡板,研制了一种以喷挡结构为先导的比例压力阀,通过外接压力传感器实现阀的输出压力控制.程光明等[13]以压电堆叠为驱动元件,通过柔性铰链放大机构放大输出位移,提出一种压电驱动型电液伺服阀前置级驱动器, 通过实验样机验证得到该驱动器固有频率为1 kHz.由于压电作动器本质上是控制位移的,因此很方便用于构成伺服阀或者比例流量阀.而用于压力比例阀时,却无法像比例电磁铁那样应用,因此以上所述研究都采用了压力传感器测量构成闭环的方式来控制压力.这在应用上带来了较大的不便,且使得构成复杂,成本增加.
本文探索一种新结构,无需压力传感器测量闭环,即可实现出口压力的比例控制.其基本原理是利用压电作动器控制先导阀开度,并通过先导阀口与先导供油器的固定节流孔的分压原理,实现对先导压力的控制.再结合主阀,即构成电液比例压力阀.由于压电作动器实际控制的是先导压力与供油压力的比例,故该阀为比例式电液比例阀.
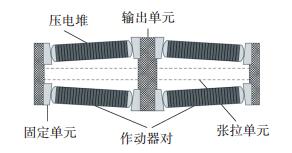
1 阀结构与工作原理设计一种电液比例阀, 如图 1所示.压电作动器固定端安装于支架上,支架安装于阀体端面.压电作动器的作动端通过连接螺栓连接到先导阀芯.先导阀芯与先导阀座配合,在座孔处形成先导节流阀口.该节流阀口开度由压电作动器控制.

|
图 1 比例式减压阀结构 Figure 1 Structure of proportional reducing valve |
由于液动力对减压阀精度造成较大影响[14],本文设计主阀芯为三台肩式结构,以减轻液动力影响.下台肩与阀体沉割槽边缘配合,形成进油节流阀口; 上台肩与阀体沉割槽配合,形成排油节流阀口; 中台肩对液流出流形成一定的导向,使其具有一定的轴向速度,从而减小进出阀芯环形腔的液流动量差,进而减小作用在阀芯上的液动力.
压力油从主阀芯下台肩上的沉割槽和径向孔进入主阀芯中间的空腔,并向上流经先导供油器的固定节流孔,然后进入先导阀口,再通过先导阀座和阀体上联通的流道流入回油口.先导供油器的固定节流与先导阀口的可变节流构成串联节流分压,改变先导阀开度,即可改变分压作用,从而控制主阀芯上腔的液压压力.
负载口的油液压力通过主阀芯上一对斜孔进入主阀芯下部中央流道,并经阻尼器的阻尼孔进入主阀芯下腔,与主阀芯上腔的液压压力平衡,实现对负载出口的压力控制.
2 比例阀建模 2.1 压电作动器模型如图 2所示,压电作动器为菱形放大差动驱动结构.驱动器带宽远高于阀响应频带,故略去其动态环节.压电作动器受到驱动电压作用,会产生成比例的位移,同时由于其自身刚度效应,在外力作用下也产生一定的附加位移.其数学模型如下:
|
图 2 压电作动器 Figure 2 Piezo actuator |
| $ {x_p} = {x_{p0}} - {K_{\rm{e}}}u + {K_{\rm{p}}}{p_{\rm{c}}}\left( {{\rm{\pi /4}}} \right)d_3^2. $ |
式中:xp为压电作动器位移(导阀芯位移),m; xp0为压电作动器初始位移(导阀芯位移),m; u为控制电压,V; Ke为压电应变常数,Ke=2.75 μm/V; Kp为柔度系数,Kp=1.1 μm/N; pc为主阀芯上腔压力,Pa; d3为可变节流口直径,m.
2.2 导阀模型导阀供油器固定节流孔流量方程:
| $ {q_1} = {c_{{\rm{d1}}}}{A_{{\rm{v1}}}}\sqrt {2\left( {{p_{\rm{s}}} - {p_{\rm{c}}}} \right)/\rho } . $ |
式中:q1为导阀供油器固定节流孔流量,m3/s; cd1为固定阻尼孔流量系数,量纲一; Av1为固定阻尼块过流面积,m2; ps为减压阀进油口压力,Pa; ρ为油液密度,kg/m3.
导阀芯阀口流量方程:
| $ {q_2} = {c_{{\rm{d2}}}}{\rm{\pi }}{d_3}{x_{\rm{p}}}\sin \alpha \sqrt {\frac{{2{p_{\rm{c}}}}}{\rho }} . $ |
式中:q2为导阀芯阀口流量,m3/s; cd2为可变节流口流量系数,量纲一; α为导阀芯半锥角,rad.
由于容腔微小,其内压缩性即压力动态予以忽略.故流量连续性方程为
| $ {q_1} - {q_2} = {A_{\rm{z}}}{{\dot x}_{\rm{z}}}, $ |
式中Az为主阀芯端面面积,m2; xz为主阀芯位移,m,向下为正.
2.3 主阀模型主阀口流量模型:
| $ {q_{\rm{z}}} = \left\{ \begin{array}{l} {c_{\rm{d}}}w{x_{\rm{z}}}\sqrt {2\left( {{p_{\rm{s}}} - {p_{\rm{c}}}} \right)/\rho } ,\;\;\;\;{x_{\rm{z}}} \ge 0;\\ {c_{\rm{d}}}w{x_{\rm{z}}}\sqrt {2\left( {p - {p_{\rm{d}}}} \right)/\rho } ,\;\;\;\;\;{x_{\rm{z}}} < 0. \end{array} \right. $ |
式中:cd为主阀阀口流量系数,量纲一; w为阀口面积梯度,m; p为负载口压力,Pa.
主阀芯运动方程:
| $ m{{\ddot x}_{\rm{z}}} + {B_{\rm{c}}}{{\dot x}_{\rm{z}}} + K{x_{\rm{z}}} + {F_0} + {F_{\rm{s}}} = \left( {{p_{\rm{c}}} - {p_{\rm{f}}}} \right){A_{\rm{z}}}. $ | (1) |
式中:m为主阀芯质量,kg; Bc为阻尼力系数,Ns/m; K为调零弹簧刚度,N/m; F0为调零弹簧弹性力,N; pf为主阀芯下腔压力,Pa.
主阀芯下腔容积小,忽略其容腔压缩性,则容腔压力
| $ {p_{\rm{f}}} = p + \frac{\rho }{2}\left( {\frac{{{A_{\rm{z}}}}}{{{c_{\rm{d}}}{A_{{\rm{vf}}}}}}} \right){{\dot x}_{\rm{z}}}\left| {{{\dot x}_{\rm{z}}}} \right|. $ |
式中Avf为反馈阻尼孔过流面积,m2.
2.4 负载腔从主阀口后至用油负载前的容腔为负载容腔.设用油负载为节流阀,其过流面积为Al,则其流量为
| $ {q_1} = {c_{\rm{d}}}{A_1}\sqrt {\frac{{2\left( {p - {p_1}} \right)}}{\rho }} , $ |
流入负载腔以及流出负载腔的流量相减后,剩余流量在容腔中建立起压力,其方程为
| $ \dot p = \frac{V}{{{\beta _{\rm{e}}}}}\left( {{q_{\rm{z}}} - {q_{\rm{l}}}} \right). $ |
式中:βe液体体积弹性模量,Pa; V为容腔体积,m3.
3 静态特性分析与液动力改善 3.1 先导压力控制特性根据以上方程,当阀处于静平衡状态时,各方程中变化项均为0,略去后得到如下方程:
| $ {p_{\rm{c}}} = \frac{{C_{{\rm{d1}}}^2A_{{\rm{v1}}}^2}}{{C_{{\rm{d1}}}^2A_{{\rm{v1}}}^2 + {{\left[ {{C_{{\rm{d2}}}}{\rm{\pi }}{d_3}\left( {{x_{{\rm{p0}}}} - {K_{\rm{e}}}u + {K_{\rm{p}}}\frac{{{\rm{\pi }}d_3^2}}{4}{p_{\rm{c}}}} \right)\sin \alpha } \right]}^2}}}. $ | (2) |
该方程为非线性方程,利用二分法求解,得到控制电压与先导压力的对应关系.
若忽略压电作动器的柔度,即不考虑负载力造成的位移,则式(2) 可简化为
| $ {p_{{\rm{c1}}}} = \frac{{C_{{\rm{d1}}}^2A_{{\rm{v1}}}^2}}{{C_{{\rm{d1}}}^2A_{{\rm{v1}}}^2 + {{\left[ {{C_{{\rm{d2}}}}{\rm{\pi }}{d_3}\left( {{x_{{\rm{p0}}}} - {K_{\rm{e}}}u} \right)\sin \alpha } \right]}^2}}}. $ |
pc、pcl和pcl-pc如图 3所示.

|
图 3 先导压力特性曲线 Figure 3 Pressure curve of pilot stage |
由图 3可以看出,刚度特性对先导压力值影响较大,设计时应予以充分考虑.从图 3中还可以看出,先导压力有一个不为0的最低值.这是由于压电作动器行程有限,先导阀口面积不可能达到无穷大造成的.
3.2 主阀压力控制特性将方程(1) 中动态项去掉,即得到主阀芯的静态平衡方程
| $ {p_{\rm{f}}} = {p_{\rm{c}}} - \left( {K{x_{\rm{z}}} + {F_0} + {F_{\rm{s}}}} \right)/{A_{\rm{z}}}. $ |
式中: F0为调零弹簧预加载力,用于调节输出压力的零点.
其他如液动力、调零弹簧力变化都对定压精度造成影响.调零弹簧的预加载力本身就很小,选择适当的初始压缩量和工作压缩量,该项影响较小,可予忽略.
液动力是造成调压精度下降的重要因素之一,特别是低压大流量阀.以比例阀典型阀压降1 MPa,流量100 L/min计,则理论上阀液动力可达
| $ {F_{\rm{s}}} = \rho {q_{\rm{z}}}\sqrt {2\Delta p/\rho } \cos \theta = 24.9{\rm{N,}} $ |
式中:Δp为阀压降,Pa; θ为射流角,θ=69°.
为此,采用三台肩式主阀芯,除与进油沉割槽和回油沉割槽相配合的台肩外,中间增加液动力补偿台肩.
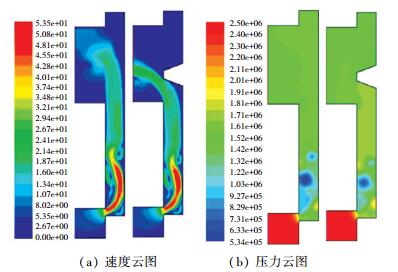
针对上述比例阀结构,设计无台阶的对比模型.流场分析是对阀内流动特性进行分析的常用方法[15],故对两种结果的模型进行流场仿真计算,得到对比模型无台肩阀结构的流场云图如图 4和图 5所示.
|
图 4 开口1 mm流场 Figure 4 Flow field contour of 1 mm opening |

|
图 5 开口-1.6 mm流场 Figure 5 Flow field contour of -1.6 mm opening |
由速度云图 4(a)可以看出, 两种情形下入口射流流场基本相同,射流呈现出一定的轴向夹角,形成轴向动量; 而出流部分,有补偿台肩的出流明显受补偿台肩的导向作用,形成了较为集中而明显的出射角,具有一定的轴向动量,入射和出射的动量差减小,因而液动力也随之减小.
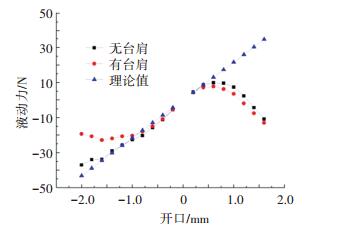
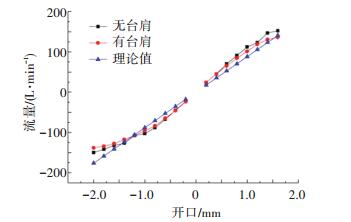
根据仿真数据得到液动力及流量曲线分别如图 6和图 7所示,可以看出,三台肩阀芯结构在不显著减少流量的前提下时液动力减小,特别是负开口条件下改善更为明显.从图中还可看出,大开度下理论计算值误差较大,即理论计算仅在小开度时成立.这与行业中液压阀的有关实验结果相符[16].造成理论值与实际结构计算值偏差的主要原因是大开口条件下,射流未及时自然扩散消失即碰撞阀芯轴颈,造成内部流场变化引起的.开口越大,阀芯轴颈等结构对流场的相对影响越大,理论计算值与流场分析值的差距也就越大.
|
图 6 主阀液动力特性 Figure 6 Flow force of main valve |
|
图 7 主阀流量特性 Figure 7 Flow characteristics of main valve |
正开口时,参见图 4的云图,入口为下方的节流口.由于中段台肩位于负载口,即出口处,入口处的流动几乎完全一致,如图 8所示.而出口处,可见由于台肩的作用,出口段轴向长度减小,流速提高,见图 9; 而无台肩的射流角在整个出口的轴向长度上,几乎都处于小射流角,仅在末端速度较低的地方有较大的射流角,所以其总体轴向动量较小,难以抵消入口段的轴向动量, 见图 10; 而有台肩的射流角在整个出口段上都较大,因而能形成较大的轴向动量,抵消入口段轴向动量, 见图 11.
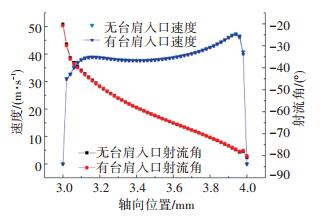
|
图 8 开口1 mm的入口速度和射流角曲线 Figure 8 Comparison of velocity and angle of inlet from different spool of 1 mm opening |
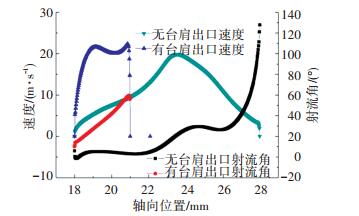
|
图 9 开口1 mm的出口速度和射流角曲线 Figure 9 Comparison of velocity and angle of outlet from different spool of 1 mm opening |
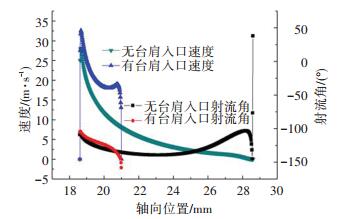
|
图 10 开口-1.6 mm的入口速度和射流角曲线 Figure 10 Comparison of velocity and angle of inlet from different spool of -1.6 mm opening |

|
图 11 开口-1.6mm的出口速度和射流角曲线 Figure 11 Comparison of velocity and angle of outnlet from different spool of -1.6 mm opening |
负开口时, 流动由负载口流入,流入和流出的速度和射流角均有一定变化,二者共同作用使液动力降低.
4 动特性仿真与分析根据以上数学方程,利用Matlab软件的Simulink搭建仿真模型.总模型主要包括主阀芯模型、先导模型、主阀口模型、负载容腔模型等.
主阀芯仿真模型具有限速、限位,能正确处理阀芯运动到端部的情况,保证仿真的正确性.
先导模型按照流量的大小,分3个区间嵌入求解非线性联立方程的算法,可覆盖全部工况,保证仿真正确性.外部实时输入参数为供油压力、回油压力、先导压力、固定阻尼面积和先导阀口面积,实时输出为先导压力.
主阀口流动仿真模型分为正方向开口和负方向开口两种工况,且覆盖了两种开口的倒灌工况.
主阀芯直径、开度等主要由静特性决定,能够影响动特性的可选参数有先导供油器节流孔径、先导阀座孔直径、阻尼器阻尼孔径以及负载的等效节流孔径.
4.1 主阀反馈阻尼孔直径影响反馈阻尼孔是影响系统动特性的最重要因素.现仅改变反馈阻尼孔的直径,设置孔直径为1.0、0.5和0.2 mm,其输出压力的动态阶跃响应特性曲线如图 12所示.其他参数为:供油孔孔径0.8 mm,先导阀座孔直径2.4 mm,负载节流阀面积3 mm2.
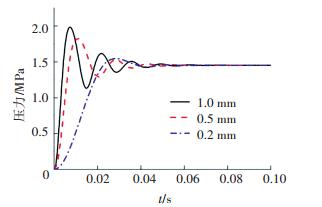
|
图 12 不同反馈阻尼孔时输出压力阶跃响应曲线 Figure 12 Step response of output pressure at different feedback damping holes |
保持阻尼孔直径为0.2 mm,负载节流阀面积3 mm2,改变先导供油器节流孔直径分别为0.8、1.0和1.2 mm,先导阀座孔直径相应地分别为2.4、3.0和3.6 mm,得到输出压力的动态阶跃响应特性曲线如图 13所示.由于面积配比关系变化,稳态压力有所变化,动特性上也略有差异,但差异性很小.这是由于阻尼器阻尼孔孔径远小于供油孔孔径,供油孔附加的阻尼作用相比较弱,故对动特性影响相对较小.
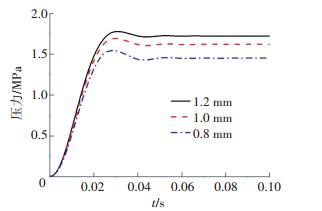
|
图 13 改变供油孔时输出压力阶跃响应曲线 Figure 13 Step response of output pressure at different supply holes |
保持供油孔孔径0.8 mm,先导阀座孔孔径2.4 mm,阻尼孔孔径0.2 mm.改变负载节流阀的节流面积分别为1、3、5 mm2.输出压力的动态阶跃响应特性曲线如图 14所示.可见负载特性也对阀后压力响应有一定的影响.
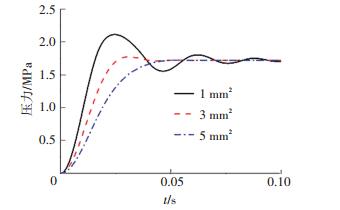
|
图 14 不同负载节流阀面积时输出压力阶跃响应曲线 Figure 14 Step response of output pressure at different areas of load throttle valve |
1) 采用本文提出的原理,无须测量压力并闭环,就可实现电液比例压力输出控制功能.
2) 由于分压的非线性效应,本比例阀输出压力-控制电压呈现较强的非线性,使用时需要进行相应的补偿.
3) 由于压电作动器行程有限,先导压力最低可控值不为0,利用调零弹簧可实现输出压力最低可控值为0.
4) 三台肩式主阀芯结构可以有效减轻液动力影响,提高阀控制精度.
5) 分析了结构参数对电液比例阀动特性的影响,表明阻尼孔和负载节流孔影响最大.通过仿真选择阻尼孔直径,使电液比例减压阀具有良好的动态特性.
| [1] |
吕超. 高速比例电磁铁动静态特性测试系统的研究[D]. 杭州: 浙江大学, 2008.
LV Chao. Research on the dynamic and static test system for high-speed propotiomal solenoid[D]. Hangzhou: Zhejiang University, 2008. |
| [2] |
卢文辉, 李胜, 吕敏健. 电液比例阀的结构原理与研究现状[J].
机床与液压, 2014(5): 166-172.
LU Wenhui, LI Sheng, LV Minjian. Fundamental working principles of electro-hydraulic proportional valves and review on their development[J]. Machine Tool & Hydraulics, 2014(5): 166-172. DOI: 10.3969/j.issn.1001-3881.2014.05.045 |
| [3] |
张弓, 于兰英, 吴文海, 等. 电液比例阀的研究综述与发展趋势[J].
流体机械, 2008(8): 32-37.
ZHANG Gong, YU Lanying, WU Wenhai, et al. Review and deve-lopment trend of electro-hydraulic proportional valve[J]. Fluid Machinery, 2008(8): 32-37. |
| [4] |
李晓娟, 李全禄, 谢妙霞, 等. 国内外压电陶瓷的新进展和新应用[J].
硅酸盐通报, 2006(4): 101-107.
LI Xiaojuan, LI Quanlu, XIE Miaoxia, et al. New headways and new applications of piezoceramics at home and abroad[J]. Bulletin of The Chinese Ceramic Society, 2006(4): 101-107. |
| [5] |
何秀华, 张习同, 杨嵩, 等. 一种合成射流压电微泵关键结构参数确定方法[J].
哈尔滨工业大学学报, 2016, 48(1): 184-188.
HE Xiuhua, ZHANG Xitong, YANG Song, et al. Critical structure parameter determination method of a synthetic jet-based piezoelectric micropump[J]. Journal of Harbin Institute of Technology, 2016, 48(1): 184-188. DOI: 10.11918/j.issn.0367-6234.2016.01.028 |
| [6] |
黄俊, 张建辉, 王守印. 多级"Y"型流管无阀压电泵的原理与试验验证[J].
光学精密工程, 2013(2): 423-430.
HUANG Jun, ZHANG Jianhui, WANG Shouyin. Theory and experimental verification on valveless piezoelectric pump with multistage Y-shape tubes[J]. Optics and Precision Engineering, 2013(2): 423-430. |
| [7] | LINDLER J E, ANDERSON E H. Piezoelectric direct drive servovalve[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2002, 4698: 488-496. |
| [8] | BAUER F, MURRENHOFF H. Piezo actuators: the future for high dynamically driven servo valves[C]//Proceedings of the 6th International Conference on Fluid Power Transmission and Control. Hangzhou: International Academic Publishers, 2005: 62-68. |
| [9] | REICHERT M., MURRENHOFF H. New concepts and design of high response hydraulic valves using piezo-technology[C]//Power Transmission and Motion Control. Bath: University of Bath, 2006: 401-404. |
| [10] |
许有熊, 李小宁. 新型压电式电-气PWM比例阀的研究[J].
中国机械工程, 2009, 20(14): 1689-1694.
XU Youxiong, LI Xiaoning. Research on a novel piezoelectric type electro-pneumatic PWM proportional valve[J]. China Mechanical Engineering, 2009, 20(14): 1689-1694. DOI: 10.3321/j.issn:1004-132X.2009.14.013 |
| [11] |
鄂世举, 杨志刚, 曲兴田, 等. 一种新型电液伺服阀[J].
压电与声光, 2004, 26(5): 377-379.
E Shiju, YANG Zhigang, QU Xingtian, et al. A new-type of electro-hydraul ic servo-valve[J]. Piezoelectrics and Acoustooptics, 2004, 26(5): 377-379. |
| [12] |
郭向东. 基于贴片式弯振模态超声电机驱动电气比例阀的研究[D]. 哈尔滨: 哈尔滨工业大学, 2012: 36-37.
GUO Xiangdong. Research on electropneumatic proportional valve driven by plate-attached type bending vibration mode ultrasonic motor[D]. Harbin: Harbin Institute of Technology, 2012:36-37. |
| [13] |
程光明, 沈传亮, 杨志刚. 压电驱动型电液伺服阀前置级驱动器实验研究[J].
西安交通大学学报, 2004, 38(1): 43-46.
CHENG Guangming, SHEN Chuanliang, YANG Zhigang. Experimental study on piezoelectric pre-stage driver of electro-hydraul ic servo valves[J]. Journal of Xi'an Jiaotong University, 2004, 38(1): 43-46. |
| [14] | HERAKOVIC N. CFD simulation of flow force reduction in hydraulic valves[J]. Tehnicki Vjesnik, 2015, 22(2): 453-463. DOI: 10.17559/TV |
| [15] | Del VESCOVO G, LIPPOLIS A. CFD analysis of flow forces on spool valves[C]//Proceedings of the 1st International Conference on Computational Methods in Fluid Power Technology. Melbourne:, 2003: 26-8. |
| [16] | AUNG N Z, JINGHUI P, SONGJING L. Reducing the steady flow force acting on the spool by using a simple jet-guiding groove[C]//International Conference on Fluid Power and Mechatronics. Harbin: IEEE, 2015. |
 2017, Vol. 49
2017, Vol. 49


