作为一种公认的高效冷却技术,双壁冷却已成功应用于飞机发动机或火箭发动机燃烧室火焰筒的冷却[1].美国埃里森公司研制的双壁冷却结构使涡前可承受温度升高超过220 K[2],已经历了耐久性测试.双壁冷却与层板冷却相比传热效果略低,但结构相对简单,流动阻力小[3].针对其传热传质特性及影响因素,许多学者制定研究方案优化主要参数以获取好的冷却效果[4-5]. Ieronymidis等[6]详细研究了窄通道的压力损失和微孔出流,用数值模拟分析表面粗糙度对传热系数的影响. Stoakes等[7]针对应用于双壁冷却的冲击结构,使用CFD耦合模拟手段研究了热传导、对流作用对其换热的影响.应用管网理论对涡轮发动机空气系统各环节的流量分配、沿程压力、温度分布的计算方法已非常成熟[8].对于叶片内冷腔室小系统,可通过管网方法迅速获得冷却通道的流动和换热参数,为叶片传热计算提供边界条件.但类似于双壁结构的新式冷却技术,其阻力特性和换热特性因叶型而异,对其应用管网方法的研究还较少.
本文构建了快速预估气冷叶片换热特性的管网算法耦合外场程序,用以指导双层壁冷却结构的设计,并借助CFX分析其流场特性.
1 管网耦合计算原理 1.1 管网计算原理管网算法是一种将复杂流动模化为一维流动单元的简便方法.很多研究人员建立航空发动机内冷系统的等效管道网络模型[9-10],快速获得流量参数,然后联合外流场实现耦合传热分析.管网算法基本的控制方程有连续性方程、动量方程和能量方程.表征流进流出守恒的连续性方程为
| $ \sum\limits_j {{q_{ij}} = 0} . $ |
微分形式的一维流管动量方程为
| $ \begin{array}{l} \left[ {1 - {{\left( {\frac{q}{A}} \right)}^2}\frac{{RT}}{{{p^2}}}} \right]\frac{{{\rm{d}}p}}{{{\rm{d}}r}} = \frac{p}{{RT}}r{\omega ^2} - \\ \frac{{RT}}{p}\frac{{{q^2}}}{A}\frac{{{\rm{d}}\left( {1/A} \right)}}{{{\rm{d}}r}} - {\left( {\frac{q}{A}} \right)^2}\frac{R}{p}\left[ {\frac{{{c_f}T}}{{2{D_{\rm{h}}}}} + \frac{{{\rm{d}}T}}{{{\rm{d}}r}}} \right]. \end{array} $ | (1) |
提出流量项q,用流进流出节点i、j上参数的平均值表示式(1) 中单元体的物理变量,将微分形式转换成差分形式,略去一些高阶小量, 经过合并得
| $ \xi \left( {{p_j} - {p_i}} \right) = {A_{ij}} - {B_{ij}}q_{ij}^2 - {D_{ij}}q_{ij}^2 - {C_{ij}}{c_f}q_{ij}^2. $ |
式中:
| $ \xi = 1 - {V^2}/\left( {RT} \right), $ |
| $ {A_{ij}} = \frac{{{p_i} + {p_j}}}{{R\left( {{T_i} + {T_j}} \right)}}\frac{{\left( {r_j^2 - r_i^2} \right)}}{2}{\omega ^2}, $ |
| $ {B_{ij}} = \frac{{8R\left( {{T_i} + {T_j}} \right)\left( {{A_j} - {A_i}} \right)}}{{\left( {{p_i} + {p_j}} \right){{\left( {{A_j} + {A_i}} \right)}^3}}}, $ |
| $ {C_{ij}} = {m_i}\frac{{2R{L_{\rm{n}}}}}{{{D_{\rm{h}}}}}\frac{{{T_i} + {T_j}}}{{\left( {{p_i} + {p_j}} \right){{\left( {{A_j} + {A_i}} \right)}^2}}}, $ |
| $ {D_{ij}} = \frac{{8R\left( {{T_j} - {T_i}} \right)}}{{\left( {{p_i} + {p_j}} \right){{\left( {{A_j} + {A_i}} \right)}^2}}}, $ |
其中Cij中mi=qij/|qij|表征流量的正负.
单元体的能量方程
| $ {q_{ij}}\left( {h_j^ * - h_i^ * } \right) = {q_{ij}}{\omega ^2}\left( {r_j^2 - r_i^2} \right)/2 + Q. $ |
式中滞止焓h*=cpT*,T*=Tc+v2/2cp,Tc=(Tc1+Tc2)/2.热量Q只包含导热传热和对流换热,由于冷却通道有不同的类别,Q分3类讨论:
1) 如果只计算内冷通道的流动和换热,Q=Ua(Tw-Tc),Tw是内壁温度,Tc是冷却空气温度. Ua=hcAc为当量换热系数,Ac是冷气侧换热面积;
2) 如果计算单腔通道两侧的叶片外壁温,Q=Ua1(Tg1-Tc)+Ua2(Tg2-Tc), 下标g表示燃气侧,1和2分别表示叶片吸力侧和压力侧;
3) 对于双壁冷却结构,一边通过固壁与外流场燃气交换热量,一边与内腔流体通过隔板等固体进行换热.以燃气侧为吸力侧,Q=Ua1(Tg1-Tc)+Uac(Tcmi-Tc). Uac是冷气侧当量换热系数,Tcmi是中间腔室的空气温度,可由前两种情况求出.
在2) 中
| $ {U_{{\rm{a1}}}} = {\left[ {\frac{1}{{{h_{{\rm{g1}}}}{A_{{\rm{g1}}}}}} + \frac{{2{\delta _1}}}{{\lambda \left( {{A_{{\rm{g1}}}} + {A_{{\rm{c1}}}}} \right)}} + \frac{1}{{{h_{\rm{c}}}{A_{{\rm{c1}}}}}}} \right]^{ - 1}}, $ |
| $ {U_{{\rm{a2}}}} = {\left[ {\frac{1}{{{h_{{\rm{g2}}}}{A_{{\rm{g2}}}}}} + \frac{{2{\delta _2}}}{{\lambda \left( {{A_{{\rm{g2}}}} + {A_{{\rm{c2}}}}} \right)}} + \frac{1}{{{h_{\rm{c}}}{A_{{\rm{c2}}}}}}} \right]^{ - 1}}. $ |
在3) 中
| $ {U_{{\rm{a1}}}} = {\left[ {\frac{1}{{{h_{{\rm{g1}}}}{A_{{\rm{g1}}}}}} + \frac{{2{\delta _1}}}{{\lambda \left( {{A_{{\rm{g1}}}} + {A_{{\rm{ce}}}}} \right)}} + \frac{1}{{{h_{\rm{c}}}{A_{{\rm{ce}}}}}}} \right]^{ - 1}}, $ |
| $ {U_{{\rm{ac}}}} = {\left[ {\frac{1}{{{h_{{\rm{ci}}}}{A_{{\rm{ci}}}}}} + \frac{{2{\delta _{{\rm{t1}}}}}}{{\lambda \left( {{A_{{\rm{ci}}}} + {A_{{\rm{ce}}}}} \right)}} + \frac{1}{{{h_{\rm{c}}}{A_{{\rm{ce}}}}}}} \right]^{ - 1}}. $ |
式中:δ1和δ2分别是通道两侧的壁厚,δt1是吸力侧双壁窄腔与主腔间固体厚度. hg是燃气侧换热系数,开始计算时给定初值,之后则提取外场计算结果. λ为叶片材质平均导热系数. hci、Aci分别为中部腔壁的对流换热系数和换热面积,Ace为贴壁窄腔里侧的换热面积,当δt1较小时,Aci≈Ace.由Q的表达式,可以将单元体的能量方程变换成3类便于温度求解的形式:
| $ {T_{cj}} = \frac{{2{U_{\rm{a}}}}}{{2{c_p}{q_{ij}} + {U_{\rm{a}}}}}{T_{\rm{w}}} + \frac{{2{c_p}{q_{ij}} - {U_{\rm{a}}}}}{{2{c_p}{q_{ij}} + {U_{\rm{a}}}}}{T_{{\rm{ci}}}} + \frac{{{q_{ij}}{\omega ^2}\left( {r_j^2 - r_i^2} \right)}}{{2{c_p}{q_{ij}} + {U_{\rm{a}}}}}, $ |
| $ \begin{array}{l} {T_{cj}} = \frac{{2{U_{{\rm{a1}}}}}}{{2{c_p}{q_{ij}} + {U_{\rm{a}}}}}{T_{{\rm{g1}}}} + \frac{{2{U_{{\rm{a2}}}}}}{{2{c_p}{q_{ij}} + {U_{\rm{a}}}}}{T_{{\rm{g2}}}} + \frac{{2{c_p}{q_{ij}} - {U_{\rm{a}}}}}{{2{c_p}{q_{ij}} + {U_{\rm{a}}}}}{T_{{\rm{ci}}}} + \\ \;\;\;\;\;\;\;\frac{{{q_{ij}}{\omega ^2}\left( {r_j^2 - r_i^2} \right)}}{{2{c_p}{q_{ij}} + {U_{\rm{a}}}}}, \end{array} $ |
| $ \begin{array}{l} {T_{cj}} = \frac{{2\left( {{U_{{\rm{ac}}}}{T_{{\rm{cmi}}}} + {U_{{\rm{a1}}}}{T_{{\rm{g1}}}}} \right)}}{{{c_p}{q_{ij}} + {U_{{\rm{ac}}}} + {U_{{\rm{a1}}}}}} + \frac{{2{c_p}{q_{ij}}\left( {{U_{{\rm{ac}}}} + {U_{{\rm{a1}}}}} \right)}}{{2{c_p}{q_{ij}} + {U_{{\rm{ac}}}} + {U_{{\rm{a1}}}}}}{T_{{\rm{ci}}}} + \\ \;\;\;\;\;\;\;\frac{{{q_{ij}}{\omega ^2}\left( {r_j^2 - r_i^2} \right)}}{{2{c_p}{q_{ij}} + {U_{{\rm{ac}}}} + {U_{{\rm{a1}}}}}}. \end{array} $ |
依据Re > 4 000湍流阶段光滑管的布拉休斯公式[11]计算孔结构(包括冲击孔、气膜孔和除尘孔等)流阻(式(2)).考虑出流结构的局部流阻损失,加入出流系数CD. CD表示实际流率与理想流率的比值.理想流率由静压Ps到总压Pt的一维等熵扩张计算.
| $ {c_f} = \frac{1}{{{{\left( {1.8\lg \mathit{Re} - 1.64} \right)}^2}}}. $ | (2) |
对于上述光滑管,用104 < Re < 1.2×105,0.7 < Pr < 100湍流充分发展段的迪图斯-贝尔特准则式[12]Nu=0.023Re0.8Pr0.4Cr来计算内壁换热.
双壁结构贴壁通道截面狭窄,黏性底层未充分发展,因此按照粗糙管处理.应用相同当量直径的尼古拉斯试验关联式cf=0.003 2+0.221Re-0.237计算流阻[11].此关联式可在105 < Re < 3×106,相对粗糙度以10%管宽计的条件下使用.使用尼林斯基(Gnielinski)公式[12]计算贴壁窄腔的内壁换热
| $ Nu = \left( {\frac{{\left( {f/8} \right)\left( {\mathit{Re} - 1000} \right)\mathit{Pr}}}{{1 + 12.7\sqrt {f/8} \left( {\mathit{P}{\mathit{r}^{2/3}} - 1} \right)}}} \right)\left( {1 + {{\left( {\frac{{{d_{\rm{h}}}}}{{{l_{\rm{s}}}}}} \right)}^{2/3}}} \right){c_{\rm{t}}}. $ | (3) |
式(3) 考虑入口效应和温差效应,估算准确度较高, 适用于流体温度和固壁温度比值0.5 < Tf/Tw < 1.5的范围. f为流阻系数,ct=(Tf/Tw)0.45,ls为通道长度,dh为当量直径.
对于叶身中段冲击孔,采用Florschuetz[13]等提出的带横向流的冲击射流冷却试验关联式:
| $ \begin{array}{l} N{u_1} = 0.363{\left( {{x_i}/{d_{\rm{m}}}} \right)^{ - 0.554}}{\left( {{y_i}/{d_{\rm{m}}}} \right)^{ - 0.422}} \cdot \\ \;\;\;\;\;\;\;\;\;{\left( {{z_i}/{d_{\rm{m}}}} \right)^{0.068}}\mathit{Re}_{\rm{D}}^{0.727}\mathit{P}{\mathit{r}^{0.333}}. \end{array} $ |
式中xi、yi、zi表示第i排冲击孔沿主流流向、展向的间距以及冲击距离,dm为冲击孔径.
气膜冷却涉及内部流体和外部流体.由式(2) 计算流阻力时,前缘、叶背和叶腹两侧的换热需进行修正:每个气膜孔的出流覆膜区域对应一个叶片壁面单元,在管网程序温度平衡计算中,根据托求得的孔出口流量和压力,对壁面单元中掺混的燃气组分进行综合,按区域取换热系数和温度的均值.
1.3 管网耦合计算方法叶片内外流体流动影响着固体域的对流传热,叶片壁面温度同时影响近壁外流场[14].气膜孔等外防护措施使内外流体又有了直接相互作用.为动态反映实际情况,需要耦合计算来模拟相互作用的叶片外部和内部流场.通常方法是借助商用CFD软件的直接耦合模拟.但在冷却方案设计过程中,常需多次改型再计算,每次都需重新划分网格,再将网格导入求解器迭代较长时间至收敛.目前, 很多涡轮叶片都具有复杂精细的冷却结构,其内部流域和叶片固体域常依赖非结构网格,致使离散过程非常耗时.管网算法能快速地确定内部流域的流动参数,省略了冷却方案初设阶段网格的划分.本文以内部流动参数为耦合条件,编写插值程序实现在交接面上与外部叶栅流道计算程序传递信息.外部程序选择哈尔滨工业大学开发的HIT-3D程序[15],其核心算法为求解TVD中心差分格式N-S方程,并提供多种黏涡模型和转捩模型,输出结果包括S1-S2流面网格点上的速度分量,以及压力、温度等. HIT-3D计算的叶栅流道采用HOH型分块结构化网格.
依据交界面上的温度连续和热流量连续条件, 编写耦合计算的插值程序:
| $ {T_{{\rm{fluid}}}} = {T_{{\rm{solid}}}},{\kappa _{{\rm{solid}}}}\frac{{\partial T}}{{\partial n}}\left| {_{{\rm{fluid}}}} \right. = {\kappa _{{\rm{fluid}}}}\frac{{\partial T}}{{\partial n}}\left| {_{{\rm{solid}}}} \right.. $ |
网格点到单元面插值.经节点坐标和相同换热边界面积判断单元面对应网格区域的横纵网格数l、m.假设网格中心点角标为ce,令ζ=[l/2],η=[m/2]([]表示取整运算),则变量v的面平均为
| $ \frac{{\sum\limits_{j = e - \eta }^{e + \eta } {\sum\limits_{i = c - \zeta }^{c + \zeta } {{v_{ij}}\Delta {x_i}\Delta {y_i}} } }}{{\sum\limits_{j = e - \eta }^{e + \eta } {\sum\limits_{i = c - \zeta }^{c + \zeta } {\Delta {x_i}\Delta {y_i}} } }} = {V_{{\rm{gc}}}}. $ |
式中Δxi、Δyi分别是网格元素横向和纵向的长度.
单元面到网格点的二维线性插值.假定网格点均布,由节点I到节点I+1,参数V变为VI,由节点I到节点J,参数V变为VJ,到节点J+1,参数V变为VJ+1.令网格中心点为
| $ \begin{array}{l} {V_A} = \left( {V + {V_J}} \right)/2,\;\;\;\;{V_B} = \left( {{V_I} + {V_{J + 1}}} \right)/2,\\ {V_C} = \left( {V + {V_I}} \right)/2,\;\;\;\;{V_D} = \left( {{V_J} + {V_{J + 1}}} \right)/2. \end{array} $ |
插值过程中网格中心点之间横向纵向网格点数是l′、m′.中心点角标为st,令ζ′=[l′/2],η′=[m′/2].则横向第i层网格中第j个网格点的参数值为
| $ {v_{ij}} = {v_i}\left( {\frac{{{V_D} - {V_C}}}{{m'}}\left( {j - t + \eta '} \right) + {V_C}} \right)/\frac{{{V_C} + {V_D}}}{2}. $ |
联系与每个单元壁厚wt相关的导热定律表达式qc=-λsΔT/wt,忽略相邻叶壁单元之间壁面切向固体导热,孔结构侧壁按照绝热处理,气膜孔出流对主流的影响按气膜修正方法处理, 建立起管网计算程序Cool_g和与HIT-3D联合运行的耦合程序HIT3D-Coolnet.参数传递包括燃气侧向固壁传递温度Tg和换热系数hf,经导热过程给管网计算提供第3类换热条件, 冷气侧提供给燃气侧壁温和流量边界条件(包括气膜出流等,属于第1类边界条件).
1.4 耦合计算验证Hylton等[16]进行的C3X叶片换热试验,测试条件与实际燃气涡轮运行工况非常相近.本文验证计算参照其4 521工况. C3X叶片流动网络的划分相对简单. 10根独立管道,从入口到出口节点划分10个单元.按从右至左从小到大的顺序给每个节点编号.叶片外壁也划分出流向和展向单元与通道位置对应,划分结果见图 1.

|
图 1 C3X叶片内部网络和壁面单元划分 Figure 1 The internal network of C3X blade and the blade wall units division |
用自编的预处理程序,读取几何文件信息,然后计算出各单元的长度、当量直径、截面面积和传热侧面积,加上冷气入口和出口的边界条件,编入管网程序的输入文件.
外流场程序使用k-ω SST湍流模型和间歇因子转捩模型.每5次外流场计算,执行一次Cool_g子程序.迭代至两边温度都达到稳定,且温度变化<0.5 K,压力变化<2 Pa时认为计算收敛.
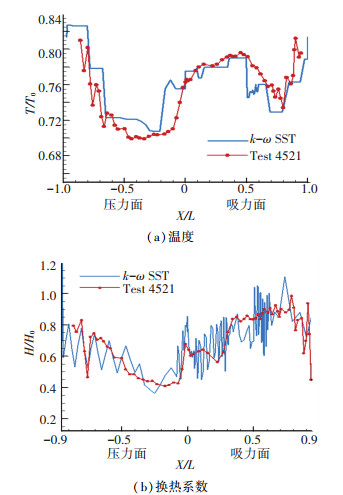
取叶片中径处耦合计算温度、换热系数与试验值相比较. 图 2横坐标0表示前缘点,负值表示吸力面,正值表示压力面,1和-1表示两侧尾缘点.
|
图 2 叶片中径壁面温度、换热系数分布曲线对比 Figure 2 The comparison of temperature and heat transfer coefficient distribution curves of blade middle radical section |
HIT3D-Coolnet所得叶片两侧壁温分布云图如图 3所示.

|
图 3 C3X叶片表面的温度分布 Figure 3 Temperature contours of C3X blade surface |
比较图 2曲线可知,HIT3D-Coolnet耦合计算能较为准确地模拟C3X叶片的内外传热过程.无论是计算值还是试验值都显示出两侧壁面温度分布中段低,前缘和尾缘高的趋势.在叶片两侧HIT3D-Coolnet所得最低温度接近试验数据最低温度.前缘点附近温度的计算结果略高于试验值,没能反映局部轻微上升的趋势.在靠近尾缘位置, 管网耦合的温度达到最高值,与实验测值相符,但变化相对较为平坦.压力面换热系数的计算值在弦向呈波浪状变化,峰值和谷值位置与冷却通道相关.从前缘点到压力面尾缘总体的上升趋势与试验值相符,在x/L=-0.76处也显示出跌入极小值并迅速回升的态势.在吸力面中部,网络耦合计算的传热系数有较大的波动范围,但平均值较接近试验值.转捩位置处换热系数走高的态势与试验值一致,但在x/L=0.4有小段下降,偏差较明显.
通过验证可知,用HIT3D-Coolnet可以较为可靠地获知气冷叶片的冷却效果.最高、最低温度的位置可得到较准确的预测.作为一种快速预测工具,管网耦合算法可用来评估冷却结构方案的优劣.
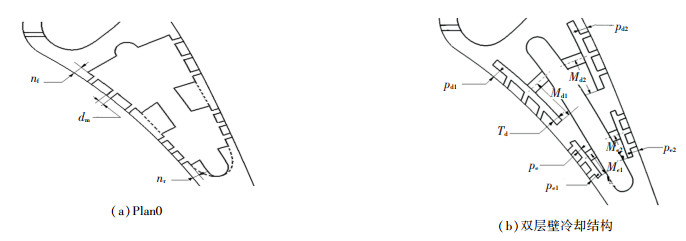
2 双层壁冷却结构建模和冷却方案设计Hylton等[16]还在C3X基础上做了前缘气膜喷淋冷却的改型设计,说明该叶型对薄腔气膜出流结构具有一定的适应性.管网方法重视的是相对通用性,可将描述多种换热元件的流阻特性和换热特性的试验关联式包含在管网程序的模型库里. 1.4节的原型算例验证了基于交接面插值过程的耦合算法的可行性.对于以C3X叶型坐标数据为基准所设计的双层壁冷却结构,主要的变化是调整了内部流路.叶盆和叶背内侧壁设置窄通道,并以可控样条绘制腔型曲线.在两侧壁面开设气膜孔,构造出冲击-双层壁-气膜复合结构,其主体为前中后3个主腔.贴壁窄腔与中腔以冲击孔连接,叶片中上部开设的气膜孔连通窄腔.管网程序获取内流场信息,继续作为外场程序的换热内边界.为证实双层壁冷却结构相比单纯气膜外防护的优势.还设计了单纯气膜外防护方案Plan0.两类结构的截面见图 4.
|
图 4 Plan0中腔截面和双层壁通道截面 Figure 4 The cross sections of Plan0 middle chamber and double-wall channel |
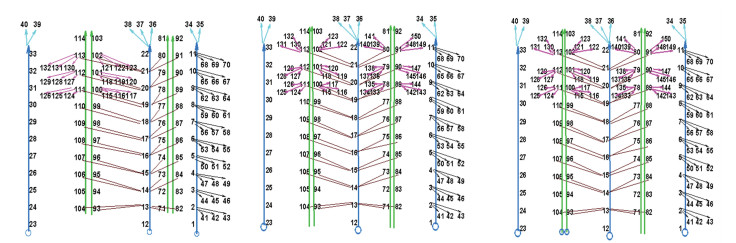
依据不同进气和出流模式,在参数化模块化建模基础上,设计3种双层壁冷却结构方案A、B、C(见图 5).
|
图 5 A、B、C方案的内部冷却通道管网计算拓扑连接图 Figure 5 The topology connection diagrams for inner cooling channel network calculation of Plan A, B, C |
图 5中41~70为前缘气膜孔. 71~81、82~92是叶腹侧两组贴壁窄通道. 93~103、104~114是叶背侧两组贴壁窄通道.圆圈表示冷气流进,箭头表示冷气流出.同样以4521工况为设计工况,分内外流场给定边界条件(见表 1、2).
| 表 1 叶栅进口 Table 1 Cascade inlet |
| 表 2 叶栅出口 Table 2 Cascade outlet |
保持原工况总的冷气流量0.170 4 kg/s不变,3种方案的冷气分配见表 3.
| 表 3 3种方案冷气入口流量 Table 3 The inlet cooling air flow of three schemes |
采用同一外流场网格下充分发展的原型流场作为初场,对每个方案运行HIT3D-Coolnet程序.平均迭代20 h后都达到收敛(叶片壁面两侧温度差别<0.5 K,外场残差<10-5).耦合计算收敛后,3种方案的叶片外壁温度结果见表 4.
| 表 4 设计工况3种方案温度计算结果 Table 4 The temperature results of three schemes in design condition |
从表 4可知,A方案最高温度最低温度都是最低的,可见受端壁加热效应较弱;B方案平均温度最低,吸力面中段低温区范围最大,由于后腔流量最少,压力面后部高温严重;C方案最高温度比原型还要高.参照C3X原型,结合云图分析,可知在设计工况下,B方案冷却效果相对最好,尤其是吸力面中上部位降温效果显著,因此作为初选方案.
3 全三维数值分析和改型设计为获取详细流动特性,对初选的方案B和参照方案Plan0建立全三维计算模型进行模拟.两者计算域都用高质量的网格来离散划分,总网格数都接近1 000万.设计工况和边界条件相同,且都采用k-ω SST湍流模型.在商用软件CFX14.0上运行7核处理器并行计算至收敛.总的仿真时间有10天(加上前处理),耗时比HIT3D-Coolnet长很多,两者所得叶壁温度见图 6.

|
图 6 Plan0和方案B的叶片壁面温度分布 Figure 6 The blade wall temperature distributions of Plan 0 and Plan B |
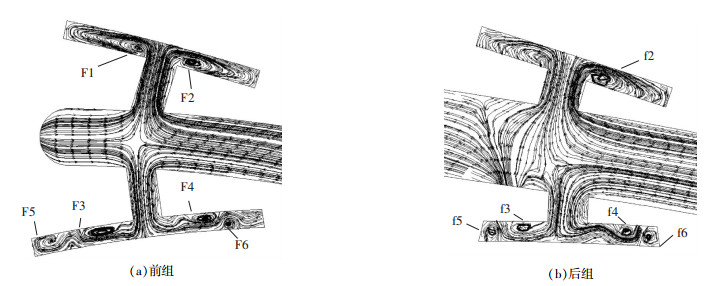
方案B的CFX模拟结果与管网耦合所得温度分布相似,吸力面中上部低温区和根顶的端部局部高温区都有反映. CFX呈现多层次的温度变化,等值线包含更多细节.方案B吸力侧中上部气膜孔附近温度比Plan0同一区域低20 K以上,而且前后两组气膜孔出流域低温区连成一块. Plan0前缘靠近压力侧的气膜孔列左边域温度较高.方案B压力侧中段气膜孔上方和下方对应贴壁窄腔的叶片表面温度低于Plan0,但是后段上部聚集最高温度,易产生热蚀.以冲击孔或气膜孔中剖面截面的速度矢量线图分析两者内流场,结果见图 7和图 8.
|
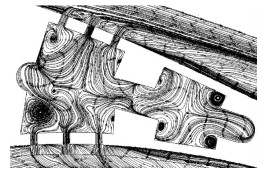
图 7 冲击孔中剖面位置的中腔和两侧窄腔内的速度矢量线 Figure 7 The velocity vector line of middle chamber and narrow cavities on two sides in impingement hole middle section |
|
图 8 Plan0中腔截面速度矢量线图 Figure 8 The velocity vector line of middle chamber section of Plan 0 |
由图 7可以看出,冲击射流在扩散过程中产生很多涡结构.上方的吸力侧冲击孔,从撞击靶面后的贴壁横流回到孔肩部,剧烈的流线卷绕产生对称于孔轴线的涡对(F1和F2,f2).红色箭头指示旋涡旋向.受到上行流影响,涡结构在窄腔空间内发展,低温冷却空气环绕侧壁伴随强烈的扰动,带走内壁热量.在压力侧窄腔每边有两个旋向相反的旋涡结构,一个是靠近里壁,大约在中间位置(F3和F4,f3和f4),另一个相对接近壁角或在对壁边缘(F5和F6,f5和f6).
Plan0中腔流道截面积的扩增使得内部流场更为混乱.最左边和最右边壁角的大旋涡是造成局部流动损失的来源.左下角旋涡的卷绕范围直径比底部中腔的宽度都要大.相比而言,方案B主要的涡结构都出现在窄腔内,流线回旋更贴近叶片外壁面,换热作用显著.
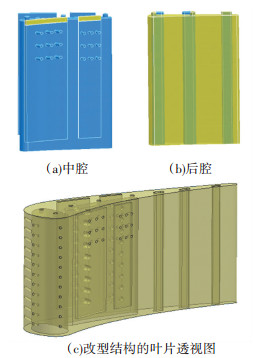
方案B压力侧冷却空气供压不足,气膜孔出流受阻.与C3X原型一样, 压力侧后部仍有相当大范围的高温区.鉴于此,改型设计采取以下措施:(1) 用扁平长圆截面直通道代替整个后腔(图 9(b)),加快冷却空气流速;(2) 为保证出流压力,压力侧贴壁窄腔的冷却空气不再从叶顶而通过气膜孔排出(图 9(a));(3) 压力侧气膜孔孔轴方向更倾向于叶片表面.
|
图 9 改型措施 Figure 9 Retrofit measures |
由图 9(a)上方可见压力侧窄腔顶部被封堵.用HIT3D-Coolnet耦合程序计算改型设计冷却结构,所得壁温分布见图 10.

|
图 10 HIT3D-Coolnet计算改型设计的壁温云图 Figure 10 Blade wall temperature contours of retrofit design calculated by HIT3D-Coolnet |
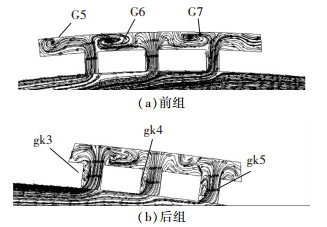
采用CFX全三维模拟改型结果(图 11),可见两种方法在大多数区域壁温分布状况相近.由于气膜孔的倾斜角度,压力侧排出的冷气很快转为主流方向且无逆流倒灌.在贴壁腔内没有明显的成核涡结构(如G5~G7),而在后组孔的孔壁左侧,也没有出现阻滞逆流的附着涡(gk3~gk5).防护膜层隔离了燃气的直接侵蚀,及时带走了固体表面上的热量,其流经表面的温度低于其上、下区域.以往的大面积集中的高温区已消失.可见在后部窄腔从整体1块变为分立的3个扁平通道使得换热效率得到改善.改型前后压力面气膜出流情况见图 12和图 13.

|
图 11 改型设计CFX模拟结果的壁温云图 Figure 11 Blade wall temperature contours of retrofit design by CFX simulation |
|
图 12 改型前压力侧窄腔和气膜孔速度矢量线图 Figure 12 The velocity vector lines in pressure side narrow cavity and film holes before retrofit |

|
图 13 改型后压力侧窄腔和气膜孔速度矢量线图 Figure 13 The velocity vector lines in pressure side narrow cavity and film holes after retrofit |
1) 试验算例验证了基于交接面插值过程的管网耦合程序的可行性.由于计算便捷且对叶片换热具有一定的模拟准确度,该程序可用于双层壁冷却方案的初步设计.
2) 双层壁复合冷却结构的窄腔具有较大换热面积,缩短了冷却侧到燃气侧的热传导距离.冷却空气从冲击孔射入撞击腔壁,形成特定的涡结构在腔内空间发展,卷绕和内部湍动促进传质与叶片的金属材料的热交换.与单纯气膜外防护相比,流阻损失较小,提高了冷却空气的利用率.
3) 改型措施弥补了初选方案中存在的不足.消除了压力侧气膜孔内逆流现象,气膜覆盖对后叶片壁起到保护作用,扁平直通道改善了叶片后部的冷却效率,局部高温得到很大程度的缓解.
| [1] |
沈国华. 火焰筒双层壁冷却的数值计算[D]. 南京: 南京航空航天大学, 2008.
SHEN Guohua. Numerical research on combustor flame tube double-walled cooling structure[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008. |
| [2] | FUNAZAKI K, TARUKAWA Y, KUDO T. Heat transfer characteristics of an integrated cooling configuration for ultra-high temperature turbine blades[C]//Experimental and Numerical Investigations: ASME Turbo Expo, 2001-GT-0148. New Orleans: International Gas Turbine Institute, 2001. |
| [3] |
苏云亮. 双层壳型涡轮导向叶片冷却设计与研究[D]. 成都: 电子科技大学, 2009.
SU Yunliang. Cooling structure design and research of double shell turbine guide vane[D]. Chengdu: University of Electronic Science and technology of China, 2009. |
| [4] | RHEE D H. Flow and heat(Mass) transfer characteristics in an impingement/effusion cooling system with crossflow[J]. Journal of Turbomachinery, 2003, 125(1): 74-82. DOI: 10.1115/1.1519835 |
| [5] | CHO H H, RHEE D H. Effects of hole arrangements on local heat/mass transfer for impingement/effusion cooling with small hole spacing[J]. Journal of Turbomachinery, 2008, 130(4): 1-11. DOI: 10.1115/1.2812325 |
| [6] | IERONYMIDIS I, GILLESPIE D R H, IRELAND P T, et al. Experimental and computational flow field studies of an integrally cast cooling manifold with and without rotation[C]//ASME Turbo Expo, GT2006-91245. Barcelona: International Gas Turbine Institute, 2006. |
| [7] | STOAKES P, EKKAD S. Optimized impingement configurations for double wall cooling applications[C]//ASME turbo expo. GT2011-46143. British Columbia: International Gas Turbine Institute, 2011. |
| [8] |
王松, 王新军, 俞茂铮. 燃气轮机空气冷却系统建模及计算分析[J].
燃气轮机技术, 2010, 12, 23(4): 33-37.
WANG Song, WANG Xinjun, YU Maozheng. Calculations and analysis of a gas turbine air cooling system[J]. GAS Turbine Technology, 2010, 12, 23(4): 33-37. DOI: 10.3969/j.issn.1009-2889.2010.04.007 |
| [9] | BONINI A, ANDREINI A, CARCASCI C, et al. Conjugate heat transfer calculations on GT rotor blade for industrial applications. Part Ⅰ-Equivalent Internal Fluid Network Setup and Procedure Description[C]// ASME Turbo Expo, GT2012-69846. Copenhagen: International Gas Turbine Institute, 2012. |
| [10] | RAMAKUMAR V N B, PRASAD S S. A combined CFD and network approach for a simulated turbine blade cooling system[J]. Indian Journal of Engineering & Materials Sciences, 2006, 13(3): 195-201. |
| [11] |
陈卓如.
工程流体力学[M]. 2版. 北京: 高等教育出版社, 2004: 261-267.
CHEN Zhuoru. Engineering fluid mechanics[M]. 2nd ed. Beijing: China Higher Education Press, 2004: 261-267. |
| [12] |
杨世铭, 陶文铨.
传热学[M]. 4版. 北京: 高等教育出版社, 2006: 246-268.
YANG Shiming, TAO Wenshuan. Heat transfer[M]. 4th ed. Beijing: China Higher Education Press, 2006: 246-268. |
| [13] | FLORSCHUETZ L W, TRUMAN C R, METZGER D E.Streamwise flow and heat transfer distributions for jet array impingent with crossflow[C]//ASME 1981 International Gas Turbine Conference and Products Show, 81-GT-77. Houston: International Gas Turbine Institute, 198l. |
| [14] | PECHIULLI A, COUTANDIN D, CIOPPO M D, et al. Development of a numerical procedure for integrated multidisciplinary thermal-fluid-structural analisys of an aeroengine turbine[C]// ASME Turbo Expo, GT2009-59875. Orlando: International Gas Turbine Institute, 2009. |
| [15] | YAN Peigang, CUI Ying, SHI Liang, et al. Modification design of turbine blade with integrated cooling structures by conjugate heat transfer and fluid network analysis[J]. Journal of Aerospace Engineering, 2014, 228(12): 2286-2299. |
| [16] | HYLTON L D, MIHELC M S, TURNER E R, et al. Analytical and experimental evaluation of the heat transfer distribution over the surfaces of turbine vanes[R]. Indianapolis:NASA, 1983: NASA-CR-168015. |
 2017, Vol. 49
2017, Vol. 49


