数控车床在机械装备中占据重要地位，其可靠性设计在很大程度上决定了加工制造的成本以及运行过程中的平均无故障工作时间(MTBF)^[1-3].可靠性分配是可靠性设计的初始阶段任务，能否合理有效地将可靠性指标分配给各子系统至关重要^[4-5].数控车床在传统意义上被视为串联系统，且各子系统的运行状态相互独立.然而，大量研究数据表明，故障独立假设不能够十分准确地描述数控车床的实际运行状态^[6-7]，建立的可靠性分配模型及得到的分配结果都具有一定偏差.因此，需要提出一种充分考虑故障相关性的可靠性分配方法.近年来，国内外学者对于可靠性分配的研究不断取得进展. Wang等^[8]提出了考虑7种不同因素的分配方法. Yadav等^[9]在Itabishi等^[10]将危害度引入可靠性分配的基础上，考虑子系统可靠性提升潜能，修正了危害度的计算公式，并提出了一种三维分析法.张义民等^[11]利用模糊数学理论，提出了一种基于数控车床故障信息的可靠性分配法. Kim等^[12]提出了严重度非线性指数化的分析方法. Mou等^[13]和张英芝等^[14]分别建立了基于Copula函数的机械系统可靠度模型，但具体形式存在差别. Chen等^[15]和唐家银等^[16]应用Copula函数，分别以子系统失效率和不可靠度比值为基础，提出了可靠性分配方法.现有分配方法对于客观故障信息的利用不够完善，且对于子系统之间的关联性考虑不够充分，对于Copula函数应用形式也不尽相同，导致可靠度模型的不统一.

本文结合数控车床故障模式、影响及危害分析(FMECA)，确定子系统严重度等级，结合三阶转换函数及观测失效率计算各子系统修正的危害度取值，并将其作为可靠性分配因素之一.分析了故障次数比重比、故障停时比重比、可靠性影响度和子系统复杂度4种分配因素.将Copula理论运用到可靠性分配中，提出一种考虑故障相关性的多因素综合分配法.通过实例及对比分析说明了分配方法的优越性.

设p维随机变量X₁, X₂, …, X_p的边缘分布函数分别为F₁(X₁), F₂(X₂), …, F_p(X_p)，且均服从[0, 1]均匀分布.称C(F₁(X₁), F₂(X₂), …, F_p(X_p))为描述p维变量的Copula函数^[17]. p维Copula函数具有如下性质和特点^[17-18]：

1) C(F₁(X₁), F₂(X₂), …, F_p(X_p))的定义域为[0, 1]^p= I^p；

2) 对于任意的F₁(X₁), F₂(X₂), …, F_p(X_p)∈I^p，C(F₁(X₁), F₂(X₂), …, F_p(X_p))对于每个F_i(X_i)都是增函数；

3) 对于任意的F₁(X₁), F₂(X₂), …, F_p(X_p)∈I^p，若存在F_α(X_α)=0，则C(F₁(X₁), F₂(X₂), …, F_p(X_p))=0；

(4) 对于任意的F₁(X₁), F₂(X₂), …, F_p(X_p)∈I^p，若除了F_α(X_α)外, 其余均为1，则C(F₁(X₁), F₂(X₂), …, F_p(X_p))= F_α(X_α).

Sklar定理^[19]指出，设p维随机变量的联合分布函数为F(X₁, X₂, …, X_p)，则存在一个Copula函数，使得

式中:若F₁(X₁), F₂(X₂), …, F_p(X_p)连续，则C(F₁(X₁), F₂(X₂), …, F_p(X_p))唯一.记u_α= F_α(X_α)，其中α=1, 2, …, p，则式(1) 可以改写为

式中F_α^-1(X_α)为F_α (X_α)的逆函数.

根据Sklar定理，F(X₁, X₂, …, X_p)的密度函数为

式中，c(.)为Copula函数的密度函数，f_α(X_α)为F_α(X_α)的密度函数.

Archimedean Copula函数是Copula函数中最为常用的一种，其表达式为

式中: 0≤u_α≤1，φ是一个非增且连续的函数，称为Copula生成元.当φ(u_α)=(－ln u_α)^1/θ时，得到的Copula即为Gumbel Copula，其表达式为

式中: θ为描述变量之间相关性的相关参数，其取值为(0, 1]. θ越接近于0，变量之间相关程度越强，当θ=1时，变量完全独立. θ的估计值可以通过极大似然估计法得到.

对于数控车床，因其结构相对复杂，整机的某个功能需要多个子系统的共同配合才能完成.某个子系统发生故障不仅与其自身材料、使用情况等因素有关，还会受到其他子系统故障的影响，这就是所谓的故障相关性^[14].对于任何两个或多个子系统，若其在结构上或功能上有重叠部分或一致性，则认为具有故障相关性. Gumbel Copula函数能够较好地描述机械系统的相关性问题^[15-16]，因此本文选取其作为连接函数.

FMECA^[20-21]是数控车床故障分析常用的方法，包括故障模式影响分析(FMEA)和危害性分析(CA). FMEA能够针对整机和子系统进行拆分，得到整机可靠性框图，并分析每个最底层零部件可能出现的故障模式及其对上一层次的影响. CA是FMECA中定量化的分析方法，其是在FMEA基础上进行的.

记第i(i=1, 2, …, N)个子系统在第j(j=1, 2, …, M)种故障模式下的严重度和发生度分别为S_ij和O_ij，其均分为10个等级，1级程度最轻，之后依次递增.传统意义上，将S_ij和O_ij的乘积作为第i个子系统在第j种故障模式下的危害度C_ij取值，则第i个子系统的危害度为

根据文献[12]，传统的严重度分级显然存在不足之处，而等级之间对应乘积对于可靠性分析意义不大，即不能简单地认为6级严重度对应造成的危害程度是3级严重度的2倍.因此，Kim等^[12]提出了一种将严重度取值进行指数化的转换，其表达式为

式中: S_ij^*为经指数转换后的严重度取值，α为转换系数，其值一般在(0, 1) 之间.取M种故障模式的最大值作为第i个子系统的严重度取值S_i^*，即S_i^*=Max(S_ij^*).

杨周等^[22]进一步分析了指数转换对于严重度取值于中低区间(1~7级)的不适用性，提出一种严重度三阶转换函数.定义FMEA严重度水平为E，则转换函数的表达式为

式中，a₀、c₀、c₁均为待定系数, 可以通过将式(3) 带入式(2) 获得；ξ为失效严重度集中水平，且$ \xi=\frac{1}{N}\sum\limits_{i = 1}^N {{S_i}} $.

式(3) 称为条件方程.其中，Λ_S可以人为确定，本文取和文献[22]相同值50.因此得到子系统的转换严重度取值$ \mathop {{S_i}}\limits^ \wedge $.根据文献[9]，将其中指数化的严重度转换值用三阶转换函数计算得到的取值代替，得到修正的危害度表达式为

式中，$ \mathop \wedge \limits_{{S_i}} $和t_i分别为归一化的三阶转换严重度和成本取值，即

式(5) 中，T_i称为降低失效率所需成本，其计算方法为

式(6) 中，λ_i为第i个子系统的观测失效率；K为成本梯度，本文取K=100.

文献[8]综合考虑了失效频率、危害度、维修性、子系统复杂度、制造工艺、工作环境和成本7个因素进行可靠性分配.本文首先将第2节论述的子系统修正的危害度作为分配因素之一.然后，基于数控机床定期监测反馈数据，忽略制造工艺和工作环境等不能从故障数据获得的因素及需要采取专家评分的主观因素，结合文献[11]，考虑故障次数、故障平均停时、可靠性影响度和子系统复杂度作为接下来可靠性分配的部分影响因素.本节主要说明除修正的危害度以外的其他4个基于故障数据及结构分析的分配因素.

故障次数比重比c_i为子系统故障次数占整机故障总次数的比例.根据收集整理到的有效故障信息，可以统计出各子系统故障次数，进而计算得到相应的故障次数比重比数值.

若第i个子系统的c_i值较大，说明该子系统出现故障的次数较多，在可靠性分配过程中应分配较高的故障率.

故障停时比重比d_i为某子系统因故障造成的平均维修时间与整机因故障造成的平均维修时间的比值.这里的平均维修时间是指除去停机时等待维修人员到来、意外因素造成维修时间浪费等因素的单纯维修时间，其能够较为全面地反应各子系统在经历故障时通过维修恢复正常工作的能力.

第i个子系统的平均维修时间越长，说明其维修性越差，应分配较低的故障率.

可靠性影响度是识别关键子系统可靠性对整机可靠性影响的一个重要指标.影响度相对较高的子系统，在整个故障周期内，对于整机失效率的贡献度就越高，因此应分配相对较低的故障率.

子系统可靠性影响度为

在求解子系统可靠性影响度时，仍将数控车床视为传统串联系统，不考虑故障相关性模型.因此，式(7) 可以改写为

子系统复杂度CM_i定义为其所含重要零部件的数目与数控机床整机所含重要零部件的比值.若第i个子系统复杂度越高，说明其包含的重要零部件的数量越多，因而出现故障的可能性就越大，在分配过程中应给予较高的故障率，且

式中: n_i即为第i个子系统所含重要零部件的数目.

以上提到的前3种分配因素都可以根据数控机床现场监测及客户反馈数据整理获得，而子系统复杂度可根据FMEA对于子系统的结构分析获得.所有的4种分配因素均是根据最真实的现场数据以及对于数控机床结构的深入了解获得，充分体现了分配的客观性和真实性.

首先建立针对各分配因素的比例矩阵B^k:

式中，β_ij^k为第k个分配因素下子系统i和j的相对值.本文考虑5个分配因素，即修正的危害度(k=1)，故障次数比重比(k=2)，故障停时比重比(k=3)，可靠性影响度(k=4) 和子系统复杂度(k=5)，β_ij^k的计算方法如式(8) 所示.

式中: ξ_i^k和ξ_j^k分别表示第i和第j个子系统在第k个分配因素下的取值.对于第k个分配因素，取比例矩阵每行的平均数

因此，针对每个分配因素可得到N个γ_ki的值，将其作为一个新矩阵Γ的第k行.这里，Γ称为综合分配矩阵，形式为

根据现有文献，权重向量W一般通过专家打分或熵权法得到.根据综合分配矩阵和权重向量得到分配向量的表达式

假设失效率分配目标值为λ_obj，若基于独立假设，将λ_obj按分配向量中的比例分配给各子系统.现考虑具有故障相关性的n个子系统，应用Copula理论建立这n个子系统的可靠度函数，如式(9) 所示:

式中，F_i(t)为第i个子系统的不可靠度，且F_i(t)=1-R_i(t). Δ为差分符号，且Δ_a^bg(x)=g(b)－g(a)，g(.)为任意函数.

数控车床共有N个子系统，若其中n个子系统具有故障相关性，则其余m=N-n个子系统相互独立.整机可靠度可以表示为

若在N个子系统中，其中n₁个子系统具有相关性，另n₂个子系统具有相关性，依此类推，得到数控车床整机可靠度为

式中: N₁, N₂, …, N_σ分别为具有故障相关性的子系统数，其和为N-m.

用$ {{\tilde{\lambda }}_{i}} $表示第i个子系统的失效率分配值，根据分配向量有

根据现有文献，选取初始阶段t=1进行分配.将λ_obj转换成可靠度指标R_obj，通常认为数控车床故障规律服从指数分布，即

以第一个子系统的失效率$ {{\tilde{\lambda }}_{1}} $为基准，其他子系统失效率根据式(11) 用$ {{\tilde{\lambda }}_{1}} $表示.当t=1时，令式(10)=R_obj= e^－λ_obj，从而解得$ {{\tilde{\lambda }}_{1}} $的值，进而得到各子系统在考虑故障相关性条件下的分配失效率值.

针对第4节提出的分配方法，本节通过数控车床实例进行分析说明.结合FMECA，将数控车床分为8个关键子系统，各子系统的观测失效率及传统严重度等级如表 1所示.

表 1

表 1 数控车床子系统严重度取值及观测失效率 Table 1 Severity values and observed failure rates of all the subsystems 子系统名称 子系统符号 Si λi/10－4 主传动系统 M 7 0.32 进给系统 F 5 0.48 冷却系统 B 4 0.64 转塔刀架 T 10 1.76 装夹附件 C 9 0.96 液压系统 H 3 0.48 电气系统 E 8 4.64 防护系统 P 1 0.16

表 1 数控车床子系统严重度取值及观测失效率 Table 1 Severity values and observed failure rates of all the subsystems

下面计算严重度三阶转换函数的表达式.前文提到，取Λ_S=50.式(2) 中，失效严重度集中水平$ \xi = \frac{1}{8}\sum\limits_{i = 1}^8 {{S_i} = 5.875} $.将式(3) 代入式(2) 得到待定系数取值分别为a₀=0.322 6, c₀=2.680 4, c₁=50.因此，对于本例，三阶转换函数的表达式为

将子系统S_i取值代入式(12) 即求得转换严重度取值，结合式(4)~(6) 得到各子系统修正的危害度取值如表 2所示.

表 2

表 2 数控车床子系统转换严重度、成本及修正的危害度取值 Table 2 Transformed severity values, costs and modified criticality values of all the subsystems 子系统符号 $ \overset{\wedge }{\mathop{{{S}_{i}}}}\, $ Ti Ci* M 34.392 6 0.103 5 1.204 0 F 19.282 6 0.099 4 0.702 8 B 12.251 9 0.096 6 0.459 2 T 50.000 0 0.086 5 2.093 7 C 46.598 9 0.092 5 1.825 5 H 6.431 0 0.099 4 0.234 8 E 41.181 3 0.076 8 1.942 2 P 1.000 0 0.110 4 0.032 6

表 2 数控车床子系统转换严重度、成本及修正的危害度取值 Table 2 Transformed severity values, costs and modified criticality values of all the subsystems

将修正的危害度作为分配的第1个因素，根据数控车床故障信息及结构信息，第3节提到的4个因素取值如表 3所示.

表 3

表 3 故障次数比重比等4种分配因素取值 Table 3 Values of four allocation factors 子系统符号 ci di Ii CMi M 0.104 1 0.069 2 0.254 6 0.104 2 F 0.115 1 0.128 9 0.260 8 0.197 9 B 0.227 4 0.062 9 0.267 1 0.046 9 T 0.164 4 0.421 4 0.316 0 0.322 9 C 0.156 2 0.069 2 0.280 3 0.145 8 H 0.158 9 0.088 1 0.260 8 0.062 5 E 0.030 1 0.094 3 0.486 8 0.072 9 P 0.043 8 0.066 0 0.248 6 0.046 9

表 3 故障次数比重比等4种分配因素取值 Table 3 Values of four allocation factors

根据表 2和表 3中的数据，计算比例矩阵B^k，进而得到综合分配矩阵

根据专家打分得到分配权重向量

进而得到分配向量

本文用t_MTBF表示整机平均无故障工作时间.要求整机MTBF达到1 500 h，即t_MTBF=1 500 h，根据指数分布的性质得到失效率分配目标值λ_obj=1/t_MTBF≈ 0.000 666 7.若基于独立假设，将λ_obj按分配向量中的比值分配给各子系统，分配结果如表 4所示.

表 4

表 4 基于独立假设的失效率分配结果 Table 4 Allocation results based on independence hypothesis 子系统符号 M F B T C H E P 失效率分配值/10-5 8.14 8.79 9.00 7.53 8.13 9.37 6.03 9.67

表 4 基于独立假设的失效率分配结果 Table 4 Allocation results based on independence hypothesis

下面考虑子系统故障相关性进行可靠性分配.首先考虑进给系统(F)和装夹附件(C)的故障相关性，其余子系统之间视为独立.得到整机可靠度为

仍取失效率分配目标值为λ_obj=0.000 666 7.记主传动系统(M)的失效率分配值为$ {{\tilde{\lambda }}_{1}} $，将其作为基准，其他子系统的失效率分配值按照分配向量中的比值用$ {{\tilde{\lambda }}_{1}} $表示，则式(13) 中各项可以表示为

取t=1及Gumbel Copula相关系数θ=0.3，并令式(13)=R_obj=e^－λ_obj，解得$ {{\tilde{\lambda }}_{1}} $并根据失效率比值得到分配结果如表 5所示.

表 5

表 5 考虑两个子系统相关性的失效率分配结果 Table 5 Allocation results when considering failure correlation between two subsystems 子系统符号 M F B T C H E P 失效率分配值/10-5 8.31 8.97 9.19 7.69 8.30 9.57 6.16 9.87

表 5 考虑两个子系统相关性的失效率分配结果 Table 5 Allocation results when considering failure correlation between two subsystems

进一步考虑所有子系统的相关性，得到分配结果如表 6所示.

表 6

表 6 考虑所有子系统相关性的失效率分配结果 Table 6 Allocation results when considering failure correlation among all the subsystems 子系统符号 M F B T C H E P 失效率分配值/10-5 10.19 11.00 11.26 9.43 10.17 11.73 7.55 12.10

表 6 考虑所有子系统相关性的失效率分配结果 Table 6 Allocation results when considering failure correlation among all the subsystems

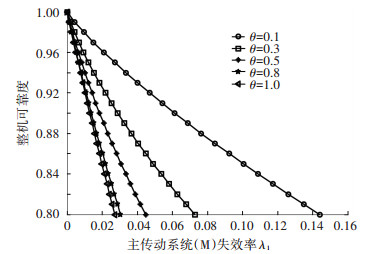
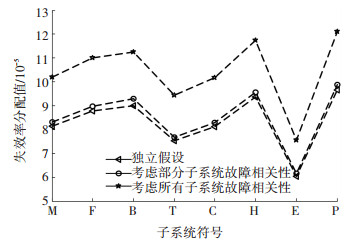
图 1是在所有子系统故障关联的情况下，当相关参数取不同值时，主传动系统(M)的分配失效率与整机可靠度之间的关系. 图 2为在独立假设、考虑两系统故障相关性和考虑所有子系统故障相关性的情况下，各子系统失效率的分配值.可以看出，在保证整机失效率分配目标值不变的情况下，考虑子系统故障相关性的可靠性分配能够使子系统得到较高的失效率，这意味着在子系统的可靠性设计上所需要的成本得以降低，对于数控机床的设计制造具有重要意义.另外，相关参数θ越小，说明子系统间相关性越强，因此在整机失效率目标值一定时，子系统分配的失效率越高.当θ=1时，子系统之间完全独立，若要达到相同的可靠性指标，分配的失效率最低.

Figure 1

图 1 主传动系统失效率与整机可靠度的关系曲线 Figure 1 Relationship between failure rate of main driving system and reliability of the lathe

Figure 2

图 2 考虑子系统不同相关性情况时失效率分配值 Figure 2 Allocation results when considering different situations of failure correlation

1) 基于数控车床FMECA，考虑子系统严重度的三阶转换函数及降低子系统失效率所需成本，建立修正的危害度表达式，充分体现了故障分析对于可靠性分配的重要作用.

2) 考虑子系统故障相关性，利用Copula函数建立整机可靠度模型，进而提出一种针对5种分配因素的可靠性分配法.选取的分配因素客观性较强，且整机可靠度模型充分研究了子系统之间的故障相关性，更加符合数控车床运行的实际状态.

3) 通过数控车床实例论证说明了本文分配方法能够充分考虑数控车床故障信息及结构信息，且考虑故障相关性的分配结果能够使得子系统在设计、生产制造中的成本得以降低，有利于数控车床的改进设计.