2. 车辆传动国家重点实验室(北京理工大学),北京 100081
2. State Key Laboratory of Vehicle Transmission(Beijing Institute of Technology), Beijing 100081, China
混合动力驱动系统具有串联式、并联式和混联式3种布置形式.功率分流混合驱动系统是混联混合动力驱动系统的一个分支,其显著特点是利用行星齿轮机构进行功率的分流与汇流[1],其转矩和转速特性互相耦合,对动力性的发挥和燃油经济性的提高提供了更大的优化空间;但系统连接方式复杂并需要多个电机协调工作,对系统参数匹配和控制提出了更多挑战[2-5].电机参数的匹配直接影响到整个功率分流式混合动力驱动系统能否正常工作,是保证混合驱动系统性能发挥的前提.电机的额定转速和峰值转矩对电机的设计和使用非常重要,影响电机的功率密度及工作性能发挥,对系统的动力性能也有重要影响.
文献[6-9]研究了串联方案中电机的功率匹配与汽车加速爬坡等性能要求的关系,没有对电机转速转矩匹配进行深入研究.文献[10-11]研究了并联方案中发动机和电机功率的匹配原则,即由发动机提供汽车平均行驶功率,由电动机提供峰值功率.关于功率分流式混合驱动方案参数匹配的研究,文献[12]提出了发电机的匹配应基于循环工况,电动机的匹配应基于加速需求的匹配原则.文献[13]提出了基于驱动电机高效区的电机额定转速匹配原则.文献[14]考虑了速比对电机功率匹配的影响,但未提出具体的匹配公式.文献[15]提出了基于优化的系统参数匹配流程,对系统的动力输出特性进行了优化,但未考虑各动力元件工作点协调问题.目前, 针对功率分流式混合驱动系统电机参数匹配的研究, 基本上是从满足驱动功率的角度对电机进行功率匹配,根据车速要求对电机进行最高转速匹配,没有考虑到发动机与电机工作点的关系,造成了发动机与电机的工作点相互制约,系统无法输出最大的动力特性.
本文介绍了双模式混合动力驱动系统的特性关系,以发挥发动机和电机最大转矩和满足系统动力性需求为匹配原则,对电机参数进行了匹配,研究了电机额定转速对发动机和两电机工作点的影响,得到了电机参数匹配公式.结合匹配实例,验证了匹配公式的正确性,为混联式混合动力汽车的性能匹配提供参考依据.
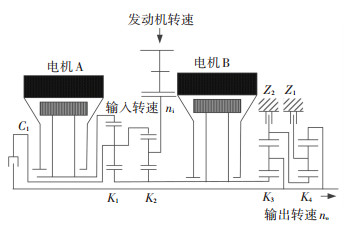
1 双模式混合动力驱动系统图 1所示为双模式混合动力驱动系统传动简图,它由4个行星排(K1、K2、K3、K4)、两个电机(A、B)以及3个操纵元件(C1、Z1、Z2)组成.其中K1和K2排起功率耦合作用,K3和K4排起变速变矩作用.采用功率分流耦合机构最突出的优点是通过两自由度行星机构的转速调节实现无级变速,所以又称为电力机械无级变速器(EVT).
|
图 1 双模式混合动力驱动系统传动简图 Figure 1 Dual-mode hybrid transmission scheme |
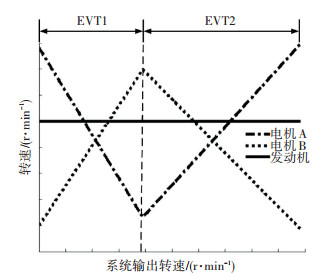
这里的模式主要是针对电机的转速变化,假定发动机输入到系统的转速不变,要使输出转速不断升高,两个电机的转速相应发生线性变化,如图 2所示.传动系统方案中共有两种驱动模式:EVT1模式和EVT2模式. EVT1模式为分速汇矩模式,电机A起到分流的作用,它抵抗发动机传到K1排太阳轮的转矩;电机B的转矩通过K3排减速增扭传递到输出轴,电机B的输出转矩越大,系统输出转矩也越大,整车动力性也越好.其中EVT1模式分为两种动力驱动工况,即EVT1L和EVT1H.
|
图 2 双模式混合动力驱动系统转速关系 Figure 2 Speed relation chat of dual-mode hybrid transmission |
EVT1模式工作时,制动器结合,离合器分离;EVT2模式工作时,离合器接合,制动器分离. 表 1为双模式混合动力驱动系统操纵逻辑表.
| 表 1 操纵逻辑表 Table 1 Maneuver logic of the system |
EVT1L一般用于爬坡工况和困难路面,能够输出较大转矩;EVT1H用于正常行驶工况中起步与加速,适用于中低速工况. EVT2模式用于中高速工况,发动机功率由K2排分流成3股:其中1股经电机B以电功率形式流向电机A,由电机A输出的机械功率与另外两股机械功率在K1排行星架汇流,经离合器C1传递到输出轴,为系统EVT2模式输出功率.
混合驱动模式下的无级调速特性通过电机A、B配合来改变系统机电功率流的功率分流比例来实现.首先对两种模式下电机A和电机B与行星排间的转速、转矩关系进行分析,得到电机A、B的转速、转矩与输入输出转速、转矩的关系,进一步分析电功率分流特性,得到分流电功率与输入功率的关系.
1.1 转速转矩关系EVT1L工况:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{n_{\rm{a}}}}\\ {{n_{\rm{b}}}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {\frac{{\left( {1 + {k_1}} \right)\left( {1 + {k_2}} \right)}}{{{k_1}{k_2}}}}&{ - \frac{{\left( {1 + {k_1} + {k_2}} \right)\left( {1 + {k_3} + {k_3}{k_4}} \right)}}{{{k_1}{k_2}}}}\\ 0&{1 + {k_3} + {k_3}{k_4}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{n_{\rm{i}}}}\\ {{n_{\rm{o}}}} \end{array}} \right],\\ \left[ {\begin{array}{*{20}{c}} {{T_{\rm{a}}}}\\ {{T_{\rm{b}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{{{k_1}{k_2}}}{{\left( {1 + {k_1}} \right)\left( {1 + {k_2}} \right)}}}&0\\ { - \frac{{1 + {k_1} + {k_2}}}{{\left( {1 + {k_1}} \right)\left( {1 + {k_2}} \right)}}}&{\frac{1}{{1 + {k_3} + {k_3}{k_4}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{T_{\rm{i}}}}\\ {{T_{\rm{o}}}} \end{array}} \right]; \end{array} $ |
EVT1H工况:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{n_{\rm{a}}}}\\ {{n_{\rm{b}}}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {\frac{{\left( {1 + {k_1}} \right)\left( {1 + {k_2}} \right)}}{{{k_1}{k_2}}}}&{ - \frac{{\left( {1 + {k_1} + {k_2}} \right)\left( {1 + {k_3}} \right)}}{{{k_1}{k_2}}}}\\ 0&{1 + {k_3}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{n_{\rm{i}}}}\\ {{n_{\rm{o}}}} \end{array}} \right],\\ \left[ {\begin{array}{*{20}{c}} {{T_{\rm{a}}}}\\ {{T_{\rm{b}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{{{k_1}{k_2}}}{{\left( {1 + {k_1}} \right)\left( {1 + {k_2}} \right)}}}&0\\ { - \frac{{1 + {k_1} + {k_2}}}{{\left( {1 + {k_1}} \right)\left( {1 + {k_2}} \right)}}}&{\frac{1}{{1 + {k_3}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{T_{\rm{i}}}}\\ {{T_{\rm{o}}}} \end{array}} \right]; \end{array} $ |
EVT2工况:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{n_{\rm{a}}}}\\ {{n_{\rm{b}}}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} { - \frac{{1 + {k_2}}}{{{k_1}}}}&{ - \frac{{1 + {k_1} + {k_2}}}{{{k_1}}}}\\ {1 + {k_2}}&{ - {k_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{n_{\rm{i}}}}\\ {{n_{\rm{o}}}} \end{array}} \right],\\ \left[ {\begin{array}{*{20}{c}} {{T_{\rm{a}}}}\\ {{T_{\rm{b}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{{{k_1}{k_2}}}{{\left( {1 + {k_1}} \right)\left( {1 + {k_2}} \right)}}}&{\frac{{{k_1}}}{{1 + {k_1}}}}\\ { - \frac{{1 + {k_1} + {k_2}}}{{\left( {1 + {k_1}} \right)\left( {1 + {k_2}} \right)}}}&{\frac{1}{{1 + {k_1}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{T_{\rm{i}}}}\\ {{T_{\rm{o}}}} \end{array}} \right]. \end{array} $ |
式中:na、nb分别为电机A、B转速,ni、no分别为系统输入转速与输出转速;Ta、Tb分别为电机A、B转矩,Ti、To分别为系统输入与输出转矩;k1、k2、k3、k4为行星排参数.
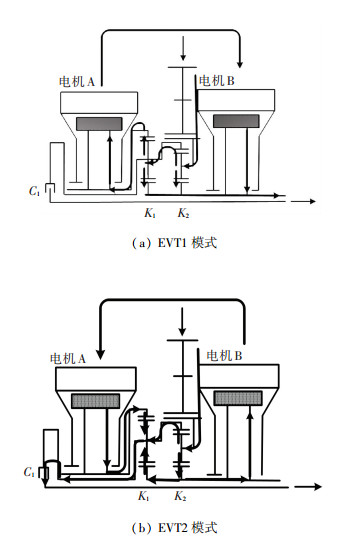
1.2 功率分流特性根据转速、转矩的大小和方向,对系统功率耦合机构的功率流进行了分析,如图 3所示.在EVT1模式下,电机A工作在发电工况,电机B处于电动工况,电机B的驱动转矩可以直接作用到输出轴,提高混合驱动系统的输出转矩.在EVT2模式下,电机B工作在发电工况,电机A处于电动工况.
|
图 3 双模式混合动力驱动系统功率流 Figure 3 Power flow of the dual-mode hybrid transmission |
设系统功率耦合部分转速与输入输出转速关系矩阵为M,且有
| $ \left[ {\begin{array}{*{20}{c}} {{n_{\rm{a}}}}\\ {{n_{\rm{b}}}} \end{array}} \right] = \mathit{\boldsymbol{M}}\left[ {\begin{array}{*{20}{c}} {{n_{\rm{i}}}}\\ {{n_{\rm{o}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} A&B\\ C&D \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{n_{\rm{i}}}}\\ {{n_{\rm{o}}}} \end{array}} \right], $ |
可推得EVT1模式下M1和电动率分流比例系数β1的表达式为
| $ \begin{array}{l} {\mathit{\boldsymbol{M}}_1}=\left[ {\begin{array}{*{20}{c}} {{A_1}}&{{B_1}}\\ {{C_1}}&{{D_1}} \end{array}} \right] = \\ \;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {\frac{{\left( {1 + {k_1}} \right)\left( {1 + {k_2}} \right)}}{{{k_1}{k_2}}}}&{ - \frac{{1 + {k_1} + {k_2}}}{{{k_1}{k_2}}}}\\ 0&1 \end{array}} \right], \end{array} $ |
| $ {\beta _1} = \frac{{{n_{\rm{a}}}{T_{\rm{a}}}}}{{{n_{\rm{i}}}{T_{\rm{i}}}}} = \frac{{{A_1} - 1}}{{{A_1}}}I - 1. $ |
EVT2模式下,M2和电动率分流比例系数β2的表达式为
| $ {\mathit{\boldsymbol{M}}_2}=\left[ {\begin{array}{*{20}{c}} {{A_2}}&{{B_2}}\\ {{C_2}}&{{D_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{{1 + {k_2}}}{{{k_1}}}}&{\frac{{1 + {k_1} + {k_2}}}{{{k_1}}}}\\ {1 + {k_2}}&{ - {k_2}} \end{array}} \right], $ |
| $ \begin{array}{l} {\beta _2} = \frac{{{n_{\rm{b}}}{T_{\rm{b}}}}}{{{n_{\rm{i}}}{T_{\rm{i}}}}} = \frac{{\left( {1 - {A_2}} \right)\left( {1 - {C_2}} \right)}}{{{C_2} - {A_2}}}I + \frac{{{A_2}{C_2}}}{{{C_2} - {A_2}}}.\\ \;\;\;\;\;\;\;\frac{1}{I} + \frac{{{A_2} + {C_2} - 2{A_2}{C_2}}}{{{C_2} - {A_2}}}. \end{array} $ |
式中:I为系统功率耦合部分速比, I=nb/ni.
2 电机参数匹配流程系统参数匹配的目的是如何匹配各部件参数,使系统能够协调工作,并发挥出最好的驱动性能,满足汽车性能的设计要求.由于双模式混合动力驱动系统中,两电机与功率耦合机构的特性关系相对复杂,本文的研究重点是对电机A和电机B的参数匹配.电机参数匹配的原则是使系统在动力工况中能够完全发挥发动机和电机的最大转矩特性,实现发动机与电机之间最佳工作点的匹配.双模式混合驱动系统电机参数匹配流程如图 4所示.

|
图 4 双模式混合驱动系统电机参数匹配流程 Figure 4 Flow chart for the motors matching of the dual-mode hybrid transmission |
由图 2可知, 混合动力驱动系统在EVT2模式下达到最大输出转速,电机A达到最高转速.此时输入转速也达到最高,整车处于最高车速工况,可求得电机A的最高转速需求为
| $ {n_{{\rm{a}}\_\max }} = \frac{{\left( {1 + {k_1} + {k_2}} \right)}}{{{k_1}}}{n_{{\rm{o}}\_\max }} - \frac{{\left( {1 + {k_2}} \right)}}{{{k_1}{i_{\rm{q}}}}}{n_{\rm{e}}}. $ |
式中:ne为发动机的额定转速,iq为系统前传动比.
从EVT1模式向EVT2模式切换时,电机B达到最高转速.根据模式切换前后电机B转速相等可得电机B的最高转速需求为
| $ {n_{{\rm{b}}\_\max }} = \frac{{\left( {1 + {k_3}} \right)\left( {1 + {k_2}} \right)}}{{\left( {1 + {k_2} + {k_3}} \right){i_{\rm{q}}}}}{n_{\rm{e}}}. $ |
整车起步加速以及爬坡等动力工况中,均允许电机短时间内使用峰值转矩.当发动机工作在最大转矩点时,可求得所需电机A峰值转矩为
| $ {T_{{\rm{a}}\_\max }} = \left| { - \frac{{{k_1}{k_2}}}{{\left( {1 + {k_1}} \right)\left( {1 + {k_2}} \right)}}{T_{{\rm{e}}\_\max }}{i_{\rm{q}}}{\eta _{\rm{q}}}{\eta _{\rm{e}}}} \right|. $ | (1) |
式中:Te_max为发动机最大转矩,ηq为系统前传动效率,ηe为发动机效率.
在EVT1L工况下,若整车起步爬坡过程中系统最大转矩需求为Tgm,即可求得电机B的峰值转矩需求为
| $ \begin{array}{l} {T_{{\rm{b}}\_\max }} = \left[ {\left[ {{T_{{\rm{gm}}}} - \left( {1 + {k_1} + {k_2}} \right)\left( {1 + {k_3} + } \right.} \right.} \right.\\ \left. {\left. {\left. {{k_3}{k_4}} \right)/\left( {{k_1}{k_2}} \right)} \right]\left| {{T_{{\rm{a}}\_\max }}} \right|} \right]/\left( {1 + {k_3} + {k_3}{k_4}} \right). \end{array} $ | (2) |
系统在EVT1H工况下的输出转矩为
| $ \begin{array}{l} {T_{\rm{o}}} = \left( {1 + {k_3}} \right)\left[ {{T_{\rm{b}}} + \left( {1 + {k_1} + {k_2}} \right)/} \right.\\ \;\;\;\;\;\;\;\left. {\left. {\left( {1 + {k_1}} \right)\left( {1 + {k_2}} \right)} \right){T_{\rm{e}}}{i_{\rm{q}}}{\eta _{\rm{q}}}{\eta _{\rm{e}}}} \right]. \end{array} $ | (3) |
根据式(3) 可知,系统输出转矩来源于两部分:第一部分是发动机转矩,第二部分是电机B转矩.将式(1) 和(2) 代入到式(3) 中,整理得到系统的最大输出转矩为
| $ \begin{array}{l} {T_{{\rm{o}}\_\max }} = \left( {1 + {k_1} + {k_2}} \right)\left( {1 + {k_3}} \right)/\left( {{k_1}{k_2}} \right){T_{{\rm{a}}\_\max }} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\left( {1 + {k_3}} \right){T_{{\rm{b}}\_\max }}. \end{array} $ | (4) |
根据式(4),即可将系统能否输出最大转矩的问题转化为能否使电机A与电机B同时输出最大转矩的问题.
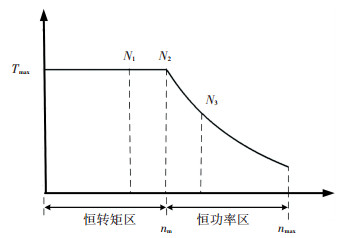
图 5为电机峰值转矩外特性曲线.在EVT1模式下, 随着车速的升高,电机A降速,电机B升速.若当发动机调速至最大转矩点转速时,两电机均工作在图 5中的恒转矩区(如N1点),则系统能够输出最大转矩特性.若此时电机A或电机B工作在N3点附近,那么受电机A的转矩限制,发动机的输出转矩受限;受电机B的转矩限制,系统输出转矩受限.所以,除了匹配电机转矩,还要匹配电机的额定转速nm,以确保当发动机调速至最大转矩点转速时,电机A和电机B至少可工作在N2点,能够发挥出最大匹配转矩.
|
图 5 电机峰值转矩外特性曲线 Figure 5 The external characteristic curve of the motor peak torque |
设电机A额定转速为nam,电机B的额定转速为nbm.已经求得EVT1模式下,电机A的电功率分流比例系数为β1.当发动机工作在最大转矩点时,发动机输入到电机A的功率为
| $ {P_{{\rm{A}}\_{\rm{i}}}} = {\beta _1}{P_{T\_\max }}{\eta _{\rm{q}}}{\eta _{\rm{e}}}. $ |
式中PT_max为当发动机工作在最大转矩点时发动机的功率.
EVT1模式下电机A处于发电状态,电机B处于电动状态.当不考虑动力电池组的功率时,系统通过电机A可向电机B提供的电功率为
| $ {P_{{\rm{B}}\_{\rm{o}}}} = {P_{{\rm{A}}\_{\rm{i}}}}{\eta _{\rm{g}}}{\eta _{\rm{m}}} = {\beta _1}{P_{T\_\max }}{\eta _{\rm{q}}}{\eta _{\rm{e}}}{\eta _{\rm{g}}}. $ |
式中:ηg为电机发电效率,ηm为电机电动效率.
若电机A能够为电机B提供足够电功率,则在车速较低时电机B会始终输出最大转矩,此时电机B功率需求为
| $ {P_{{\rm{B}}\_{\rm{c}}}} = {n_{\rm{b}}}{T_{{\rm{b}}\_\max }}/9549. $ |
所以若要电机A与电机B同时输出最大转矩,需要满足
| $ {P_{{\rm{B}}\_{\rm{o}}}}{\eta _{\rm{m}}} \ge {P_{{\rm{B}}\_{\rm{c}}}}. $ |
式中ηm为电机电动效率.
可求得电机B额定转速nbx应满足
| $ {n_{{\rm{bx}}}} \ge \frac{{{P_{T\_\max }}{\eta _{\rm{q}}}{\eta _{\rm{e}}}{\eta _{\rm{g}}}{\eta _{\rm{m}}}}}{{\frac{{{P_{T\_\max }}{\eta _{\rm{q}}}{\eta _{\rm{e}}}{\eta _{\rm{g}}}{\eta _{\rm{m}}}\left( {{A_1} - 1} \right)}}{{{A_1}{n_{\rm{i}}}}} + \frac{{{T_{{\rm{b}}\_\max }}}}{{9549}}}}. $ | (5) |
从而得到电机A额定转速nax应满足
| $ {n_{{\rm{ax}}}} \ge {A_1}{n_{T\_\max }}/{i_{\rm{q}}} + {B_1}{n_{{\rm{bx}}}}. $ | (6) |
式中nT_max为当发动机工作在最大转矩点时发动机的转速.
根据式(5) 和式(6) 可知,电机额定转速选择的约束是充分发挥发动机和电机转矩匹配的最优值,要根据工程实现进行最终确定;另外,根据这一组临界电机参数计算所得的系统加速时间未必能够满足系统对加速特性的要求,所以需要根据满足加速时间的要求对电机额定转速进行适当的调整.
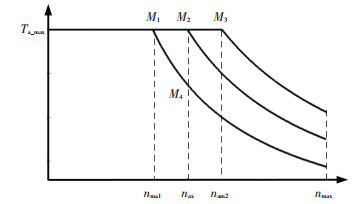
以电机A为例对额定转速匹配结果进行说明. 图 6为峰值转矩与最高转速相同,额定转速不同的三组电机A峰值转矩外特性曲线.图中Ta_max是根据式(1) 匹配的电机A峰值转矩;nax是为保证发动机和电机B输出最大转矩,电机A额定转速的临界最小值.
|
图 6 不同额定转速下电机A转矩外特性曲线 Figure 6 External characteristic curves of motor A for different rated speed |
若匹配电机A额定转速为nam1,当发动机调速到最大转矩点转速nT_max时,电机A受转速约束只能工作在M4点,发动机转矩受电机A转矩限制,系统无法发挥发动机最大转矩.若匹配电机A额定转速为nam2,当发动机调速到nT_max时,电机A如果工作在M3点,系统可发挥出发动机最大转矩;随着车速的增加,电机A工作点沿外特性从M3到M2迁移的过程中,发动机会一直工作在最大转矩点直到电机A降速至临界额定转速nax.
4 电机参数匹配实例某双模式混合动力重型车辆设计指标为最高车速不低于100 km/h,最大爬坡度大于31°,0~60 km/h加速时间<20 s;车体参数取整备质量21 t,滚动阻力系数0.013,风阻系数0.6,迎风面积5.5 m2,车轮半径0.59 m;发动机参数为额定功率300 kW,额定转速2 100 r/min,最大转矩1 732 N·m,最大转矩点转速1 400 r/min;电池充放电功率为100 kW.另外,混合驱动系统结构参数如表 2所示.
| 表 2 系统结构参数 Table 2 System structural parameters |
按照所述流程进行电机参数匹配, 计算结果如表 3中的计算值所示.本文利用MATLAB中的优化程序,以系统输出最大转矩为优化目标,计算整车牵引特性;在整车加速时间的校核过程中考虑了电池放电影响,最终得到电机参数如表 3中匹配值所示.
| 表 3 电机参数匹配结果 Table 3 Results of the motors' parameters matching |
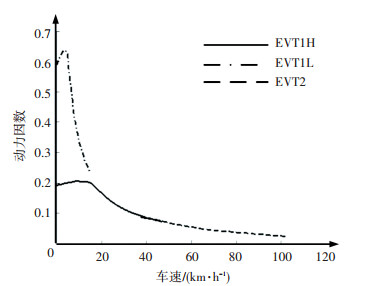
图 7为整车牵引特性曲线,满足最高车速100 km/h和31°爬坡度(需求动力因数为0.54) 的要求.
|
图 7 整车牵引特性曲线 Figure 7 The vehicle tractive characteristics |
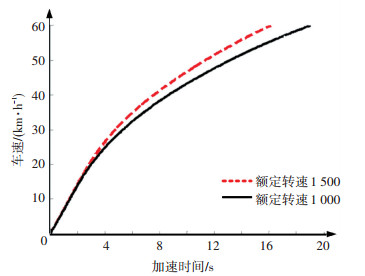
为了验证本文提出的电机参数匹配方法,采用额定转速分别为1 000和1 500 r/min,最高转速和峰值转矩均相同的两组电机参数进行加速特性对比, 结果如图 8所示.采用1 500 r/min计算得到整车0~60 km/h加速时间为16.2 s(不考虑换挡时间),比采用1 000 r/min计算得到整车0~60 km/h加速时间减少了2.9 s.
|
图 8 整车加速特性曲线对比 Figure 8 The vehicle accelerating characteristics comparison |
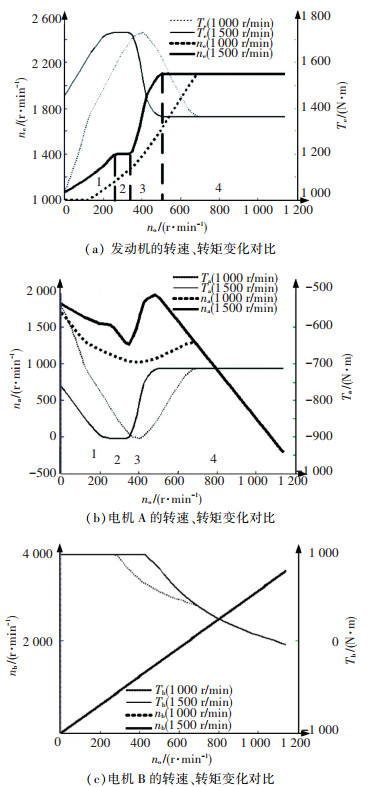
在EVT1模式下,对1 000、1 500 r/min两组电机参数得到的整车动力工况中发动机和电机的转速、转矩随系统输出转速的变化进行分析对比,结果如图 9所示.
|
图 9 EVT1模式下各动力元件转速、转矩变化对比 Figure 9 Speed & torque comparison of power components in EVT1 |
通过对比表明,采用1 500 r/min计算得到的系统输出转速在270~330 r/min时,发动机可与两电机一起为系统提供最大的转矩输出.而1 000 r/min则不能在同一系统输出转速下,使发动机和两电机共同输出最大转矩.
根据采用1 500 r/min分析得到的发动机转速变化,将系统在EVT1模式下的工作状态分为4个阶段:
1) 发动机启动升速,电机A降速,电机B升速.由于电机A转速较高,电机A的工作点位于恒功率区的外特性曲线上;电机B转速较低,电机B的工作点位于恒转矩区的外特性曲线上.
2) 发动机升速到最大转矩点转速1 400 r/min,电机A转速降至额定转速1 500 r/min附近.此时,发动机稳定工作在最大转矩点,电机A和电机B均工作在恒转矩区的外特性曲线上,即发动机与两电机在此阶段共同输出最大转矩,因而系统开始输出最大转矩.
3) 电机A转速降至1 230 r/min附近时,发动机工作点从最大转矩点向最大功率点迁移,发动机开始升速.电机A的工作点从恒转矩区的外特性曲线向输出大功率的工作点迁移,电机B的工作点受电机A的输出功率影响.
4) 发动机稳定工作在额定功率点,电机A继续降速,电机B继续升速.电机A的输出转矩保持恒定,电机B的输出转矩降低.
综合以上分析可知,采用本文提出的基于系统最大动力特性的电机参数匹配方法,可使发动机和两电机同时为系统提供最大转矩输出,使系统获得最佳的动力特性;通过对两电机额定转速的匹配,可控制系统最大转矩输出时系统输出转速的范围.
5 结论1) 介绍了双模式混合动力驱动系统的特性关系,以完全发挥发动机和两电机的最大转矩为目标,研究了双模式混合动力驱动系统电机参数匹配的原则和方法,提出了电机额定转速、峰值转矩等电机参数匹配解析表达式.
2) 通过合理匹配电机额定转速可使发动机和电机同时在最大转矩点工作,并可对此时系统的输出转速范围进行控制,实现了发动机参数与电机参数之间最优工作点的匹配.
3) 结合参数匹配实例,详细分析了双模式系统在两种模式下发动机和电机的工作状态,验证了电机匹配原则的正确性.本文研究对于混联式混合动力汽车性能分析和系统参数匹配具有实际应用价值.
| [1] |
韩立金. 功率分流混合驱动车辆性能匹配与控制策略研究[D]. 北京: 北京理工大学, 2010.
HAN Lijin. A study on performance matching and control strategy for power-split hybrid electric vehicles[D]. Beijing: Beijing Institute of Technology, 2010. |
| [2] | CIPEK M, PAVKOVIÉ D, PETRIÉJ. A control-oriented simulation model of a power-split hybrid electric vehicle[J]. Applied Energy, 2013, 101(1): 121-133. DOI: 10.1016/j.apenergy.2012.07.006 |
| [3] | WANG Y, SUN D Y. Powertrain matching and optimization of dual-motor hybrid driving system for electric vehicle based on quantum genetic intelligent algorithm[J]. Discrete Dynamics in Nature & Society, 2014, 2014(5): 10-14. DOI: 10.1155/2014/956521 |
| [4] | HALVAI Niasar A, MOGHBELLI H, VAHEDI A. Design metho-dology of drive train for a series-parallel hybrid electric vehicle (SP-HEV) and its power flow control strategy[C]//2005 IEEE International Conference on Machines and drives. SanAntonio: Institute of Electrical and Electronics Engineerings Computer Society, 2005: 1549-1553. DOI: 10.1109/IEMDC.2005.195926. |
| [5] | KANG J, CHOI W, HONG S, et al. Control strategy for dual-mode power split HEV considering transmission efficiency[C]//2011 IEEE Vehicle Power and Propulsion Conference, VPPC 2011. Chicago: IEEE Power Electronics and Vechicular Tecnology Societies, 2011:1-6. DOI: 10.1109/VPPC.2011.6043008. |
| [6] |
张志超. 串联式混合动力汽车动力系统参数匹配及性能仿真研究[D]. 西安: 长安大学, 2014.
ZHANG Zhichao. The parameters matching and performance simulation of series hybrid electric vehicle powertrain[D]. Xian: Chang'an University, 2014. |
| [7] | GAO Yimin, MEHRDAD E. Parametric design of the traction motor and energy storage for series hybrid off-road and military vehicles[J]. IEEE Transaction on Power Electronics, 2006, 21(3): 749-755. DOI: 10.1109/TPEL.2006.872374 |
| [8] |
邱利宏, 钱立军, 程伟, 等. 插电式串联混合动力汽车参数匹配及控制策略研究[J].
汽车工程学报, 2014, 4(4): 297-303.
QIU Lihong, QIAN Lijun, CHENG Wei, et al. Parameters match-ing and control strategy of plug-in series hybrid electric vehicles[J]. Chinese Journal of Automotive Engineering, 2014, 4(4): 297-303. DOI: 10.3969/j.issn.2095-1469.2014.04.10 |
| [9] |
孙永正, 李献菁, 邓俊, 等. 插电式串联混合动力轿车的选型匹配与仿真[J].
汽车工程, 2010, 32(12): 1015-1020, 1025.
SUN Yongzheng, LI Xianjing, DENG Jun, et al. Type selection, matching and simulation of plug-in series hybrid electric car[J]. Automotive Engineering, 2010, 32(12): 1015-1020, 1025. |
| [10] |
舒红, 彭大, 袁月会, 等. 插电式并联混合动力汽车动力传动系统与控制参数匹配设计[J].
汽车工程学报, 2012, 2(2): 105-112.
SHU Hong, PENG Da, YUAN Yuehui, et al. Matching design of power train and control parameters for a plug-in parallel hybrid electric vehicle[J]. Chinese Journal of Automotive Engineering, 2012, 2(2): 105-112. DOI: 10.3969/j.issn.2095-1469.2012.02.004 |
| [11] |
高爱云, 王邦军, 郭志军, 等. 并联混合动力系统参数匹配优化研究[J].
机械设计与制造, 2014(11): 235-238, 242.
GAO Aiyun, WANG Bangjun, GUO Zhijun, et al. Study on optimization for parameters of powertrain system of parallel hybrid electric vehicle[J]. Machinery Design & Manufacture, 2014(11): 235-238, 242. DOI: 10.3969/j.issn.1001-3997.2014.11.066 |
| [12] | BEHROOZ M, EMADI S A M. Dual-mode power-split transmission for hybrid electric vehicles[J]. IEEE Transactions on Vehicular Technology, 2010, 59(7): 3223-3232. DOI: 10.1109/TVT.2010.2049870 |
| [13] | LU B, CHEN H, HE H, et al. The dynamic matching calculation and simulation for dual-motor driven electric vehicle[C]//IEEE Transportation Electrification conference and EXPO, ITEC, Asia-Pacific 2014-Conference Proceeding. Beijing: Institute of Electrical and Electronics Engineers Inc, 2014:1-5. DOI: 10.1109/ITEC-AP.2014.6941122. |
| [14] |
韩立金, 项昌乐, 刘辉, 等. 双模式混合驱动装置电机参数匹配[J].
吉林大学学报(工学版), 2011, 41(6): 1527-1531.
HAN Lijin, XIANG Changle, LIU Hui, et al. Motors matching of the dual-mode hybrid transmission[J]. Journal of Jilin University Engineering and Technology Edition, 2011, 41(6): 1527-1531. |
| [15] |
韩立金, 刘辉, 王伟达, 等. 功率分流混合动力汽车参数匹配与优化研究[J].
汽车工程, 2014(8): 904-910.
HAN Lijin, LIU Hui, WANG Weida, et al. A study on the parameter matching and optimization of a power split HEV[J]. Automotive Engineering, 2014(8): 904-910. |
 2017, Vol. 49
2017, Vol. 49


