加热炉是连接连铸和轧线的关键中间设备，起到加热板坯，使之达到轧制温度的作用.因此，为了获得好的加热质量，减少氧化烧损，节能降耗，需要针对不同钢种、规格的板坯，优化其升温曲线，并据此对加热炉每个控制段设定相应的炉温. Fujii等^[1]建立基于混合逻辑动态模型表示的控制模型，解决了温度控制问题；Steinboeck等^[2]用准牛顿方法求解非线性无约束的动态优化问题；Han等^[3]对加热炉进行了三维非定常数值模拟，对板坯最佳停留时间进行了优化；Steinboeck等^[4]以加热炉温度的计划参考轨迹优化实现板坯热量的增加；杨业建等^[5]通过优化计算得到板坯的理想升温曲线和相应的炉温制度；孟祥^[6]提出了基于内点法的加热炉炉温优化模型的求解算法，得到稳态条件下的炉温设定值；景会成等^[7]以最小化燃料消耗为目标函数，利用可变容差法求得炉温的最优分布.在权值分配问题中，Duan等^[8]用出版数，影响因子和引用率等评价指标，采用熵权-TOPSIS法对期刊进行评价；虽然Thakur等^[9]和Deere等^[10]分别将TOPSIS法应用于工程领域，但对于加热炉控制领域却鲜有人涉及.

在实际生产中，每个控制段内会同时加热多块板坯，各个板坯所处的状态不同，其对当前控制段的炉温要求也不尽相同，因此需要根据当前控制段内所有板坯的需求调节当前控制段的炉温设定.

本文首先通过传热模型和炉温优化模型，得出针对单块板坯的最佳加热策略；然后引入在线变权重方法——熵权-TOPSIS法(entropy weight-technique for order preference by similarity to ideal solution, EW-TOPSIS)对每块板坯对应的炉温设定不同的权值，从而加权得到本控制段内的综合炉温设定值.

考虑到在线应用和模型的精度，本文采用二维非稳态方程进行板坯温度的求解.加热炉横断面方向上的炉温是近似相等的，可以认为板坯长度方向的温度也相等.建立板坯二维导热模型：

式中：c为板坯的比热容，J·(kg·K)^-1；λ为板坯的导热系数，W·(m·K)^-1；T为单元温度，K；ρ为板坯的密度，kg·m^-3；x和y为板坯宽度和厚度方向的长度，m；τ为时间，s.

采用总括热吸收率法计算板坯边界条件，并认为板坯边界的热流密度是相同的，总括热吸收率法表示的热流密度为

式中：q为热流密度，J/(m²·s)；σ为Stefan-Boltzmann常数，σ=5.67 W/(m²·K⁴)；Φ_CF为总括热吸收率；T_f和T_s分别为炉温和板坯表面温度，K.根据板坯内部传热模型和边界条件，本文建立二维交替隐式差分模型：在t~t+1/2时刻，y方向隐式，x方向显式；在t+1/2~t+1时刻：x方向隐式，y方向显式.采用追赶法求解方程组，即可求得每个时间步长内所有单元的温度，以此作为炉温优化和设定模型的基础.

炉温优化是在板坯传热数学模型基础上，通过考虑板坯加热温度的要求，优化计算得到板坯在加热过程中的炉温制度及当前加热条件下的理想升温曲线，进而实现加热炉的热工优化控制^[11].文献[12-13]分别建立了基于炉温的目标函数, 并采用不同的优化方法对单块板坯所对应的炉温进行了计算.本文将加热炉模型分为热回收段、预热段、加热一段、加热二段、均热段，这5个控制段的炉温即为优化的目标温度.把5个控制段的炉温拟合即可得到理想的炉温曲线.由1.1节中的传热模型，可得到板坯的理想升温曲线和相应的炉温设定.根据加热炉生产的工艺要求，如果板坯表面温度对炉长的积分值最小，则加热过程的能耗最小，建立如下目标函数：

式中：T_s为加热过程中板坯表面温度的平均值，K；L为炉长，m.求得目标炉温使得J的值最小，即min J.根据断面温差、表面温差、升温速度等工艺要求，建立如下约束条件：

式中：Δt为时间步长，s；ΔT_s(max)^v为最大升温速率，K/s；T^*为目标出炉温度，K；ΔT为出炉目标最大温差，K；T_c为板坯中心温度，K；ΔT_s(max)为出炉最大断面温差，K；T_f为炉温，K；T_{f min}和T_{f max}分别为炉温上下限，K；i为炉段.根据以上目标函数和约束条件，采用遗传算法得到针对某块板坯的最优加热策略和升温曲线.炉温优化流程图如图 1所示.

Figure 1

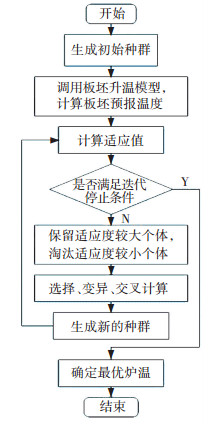
图 1 炉温优化程序框图 Figure 1 The diagram of temperature optimization program

以上的炉温优化过程是针对单块板坯的，即每块板坯对应一个最优升温曲线和炉温设定值.还需要综合考虑当前控制段内所有板坯的不同状态对炉温进行综合设定.

在一般的多目标决策问题中，无论是评价指标还是待评项目往往是固定的，只需要根据固定值进行离线优化计算即可.但是在加热炉生产中，由于板坯的移动和温度的变化，其评价指标和待评项目(板坯的属性和板坯)是不断变化的，且这种变化会有成千上万种，如果对每一种情况进行专家判定，工作量巨大.而主观赋权评价法是根据决策者对各项评价指标的主观重视程度来赋值的一种方法^[14]，所以其不可能应用在在线炉温设定上.

在客观赋权评价法中，熵权法操作性和客观性强.其基本原理是某指标的数值差异越大，则信息熵越小，该指标提供的信息量越大，其权重便越大^[15].但是熵权表示的是各指标竞争的激烈程度，而不是各指标的实际重要程度.当所有熵值都趋近于1时，即使微小的差距都会引起熵权成倍数地变化，导致部分指标被赋予了与其重要性不符合的权重^[16]. TOPSIS法是一种逼近理想解法的排序方法，该方法反映了备选方案和理想方案位置上的一致性，是由HWANG等^[17]首先提出的. TOPSIS模型是一种距离综合评价法，通过在目标空间中定义一个测度，以此测量目标靠近正理想解和远离负理想解的程度来评估方案的权重.但是TOPSIS法在构造加权规范化矩阵的过程中需要用到主观权重，因此本文用熵权代替此权重.

1) 设有m个待评项目，也就是板坯数；n个评价指标，也就是板坯当前属性，即温差、位置、厚度、钢种；形成原始数据矩阵X=(x_ij)_m×n，并对其进行标准化得到矩阵R=(r_ij)_m×n：

2) 计算第j个属性下第i个板坯指标值的比重p_ij：

3) 计算第j个属性的熵值e_j：

4) 计算第j个属性的熵权w_j：

5) 将熵权w_j与目标矩阵R=(r_ij)_m×n中对应的指标相乘，得到规范化矩阵V=(v_ij)_m×n：

6) 确定理想解和负理想解：

7) 计算对象到理想解和负理想解的距离：

8) 计算相对贴近度：

9) 把相对贴近度归一化得到每块板坯的权值：

板坯实时温度是炉温设定必须考虑的因素，板坯温度的高低直接影响当前炉温的设定值.在板坯前进的过程中，距离出炉门越近的板坯，其温度影响更大，所以板坯在控制段内的位置也会影响炉温设定值.不同的钢种，对于其温度要求的严格性也不相同，部分钢种对温度要求较为严格，必须保证其出炉温度达到目标值.因此，本文引入特殊钢种等级的概念，对不同的钢种，根据其温度严格性的要求不同划分不同的等级.此外，由于板坯厚度不同，其加热时间也不同，所以还必须考虑板坯厚度的影响.

根据以上几点，本文选取的评价指标为板坯当前温度与理想温度的差值、板坯在当前控制段的位置、板坯厚度和特殊钢种等级.待评方案为每个板坯对应的炉温设定值.本文提出的炉温综合设定程序的框图如图 2所示.

Figure 2

图 2 炉温综合设定程序框图 Figure 2 The diagram of temperature comprehensive setting program

根据某热轧厂的实际情况，以加热二段为当前控制段，其长度为13.2 m.根据布料中对板坯间隙的要求，控制段内最大的板坯数量为8，以1.45 m宽的板坯为例.设板坯以54 mm/s的速度匀速前进.为了使仿真实验更符合生产实际，随着板坯向前运动，首先依次装入8块按照理想加热曲线加热的板坯(Ⅰ1组板坯)，即板坯无温度偏差，再依次装入有温度偏差的16块板坯(S组板坯)，最后再装入8块无温度偏差的板坯(Ⅰ2组板坯).

16块板坯均为实际生产数据，其中钢种等级越大代表板坯对温度的要求越严格.以Q235B、SPHC、Q345B、W600等4个钢种为例，计算出升温曲线和加热二段的炉温设定值.其初始基本数据如表 1所示，为使数据信息更符合工程实际，现将温度单位转换为℃.

表 1

表 1 模拟实验板坯初始参数 Table 1 Simulated experimental initial parameters of slab 板坯编号 钢种 钢种等级 厚度/mm 当前理想板温/℃ 温度偏差/℃ 加热二段优化炉温/℃ S1 W600 1 230 1 020 20 1 226 S2 W600 1 230 1 020 23 1 233 S3 SPHC 2 230 1 030 33 1 238 S4 W600 1 230 1 020 19 1 226 S5 Q345B 3 250 1 068 29 1 273 S6 Q345B 3 250 1 068 41 1 273 S7 Q345B 3 250 1 068 38 1 273 S8 Q235B 4 250 1 080 43 1 285 S9 SPHC 2 240 1 050 35 1 233 S10 SPHC 2 240 1 050 30 1 235 S11 SPHC 2 240 1 050 28 1 233 S12 SPHC 2 240 1 050 34 1 246 S13 W600 1 230 1 048 27 1 263 S14 Q235B 4 230 1 077 24 1 285 S15 Q235B 4 230 1 077 20 1 285 S16 Q235B 4 230 1 077 18 1 285

表 1 模拟实验板坯初始参数 Table 1 Simulated experimental initial parameters of slab

在开始阶段，首先对炉温进行一次加权计算并设定计算炉温.每当控制段内有新的板坯进入后，重新进行计算.根据图 2程序框图，建立综合炉温设定模型，对16块板坯进行仿真计算，结果见表 2.

表 2

表 2 实验前后温差对比 Table 2 Comparison of temperature difference before and after experiment 板坯编号 初始温度差/℃ 实验后温度差/℃ S1 20 3.19 S2 23 4.89 S3 33 8.41 S4 19 1.48 S5 29 5.65 S6 41 11.42 S7 38 10.19 S8 43 13.58 S9 35 8.53 S10 30 9.26 S11 28 7.25 S12 34 8.63 S13 27 9.81 S14 24 3.49 S15 20 1.62 S16 18 -0.11

表 2 实验前后温差对比 Table 2 Comparison of temperature difference before and after experiment

由表 2可知，在当前控制段使用综合炉温设定值后，板坯实际温度与理想温度的温差实现较大程度的下降.各板坯在炉内的温差变化见图 3.由图 3可以看出，无论板坯的初始温差为多少，在经过当前加热段后，板坯温差均有下降且基本没有超调即高于理想板温的情况出现.

Figure 3

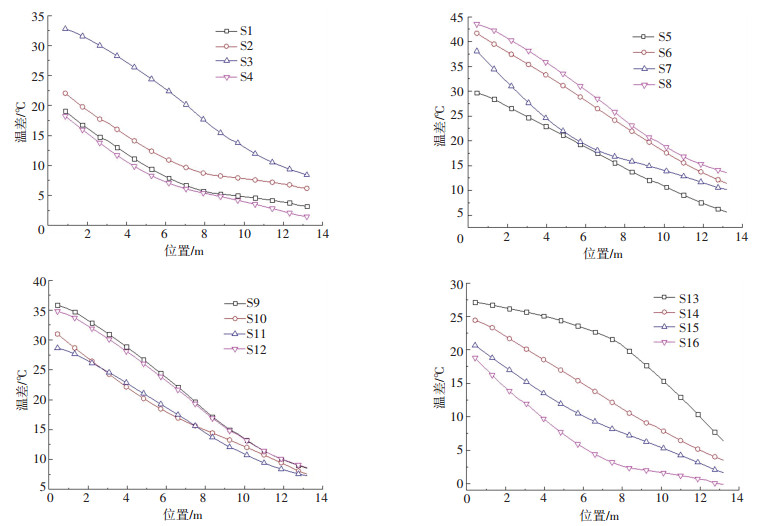
图 3 S组板坯的温差变化 Figure 3 Temperature difference of slab in S group

为了体现模型在综合炉温设定方面的优势，选取工业生产中常用的炉温权值设定方法与本文的模型进行比较.工业生产中常用的方法为固定权值模型，此模型只考虑板坯位置，即本段中距离出炉门最近的板坯的设定炉温即为本控制段的炉温.此外，本文还选取了原始的熵权模型来进行对比，对比结果如表 3所示.

表 3

表 3 3种模型实验数据对比 Table 3 Experimental data comparison of three models ℃ 模型 平均温差 最大温差 实验前 实验后 实验后 熵权-TOPSIS法 28.86 6.51 13.58 熵权法 28.86 10.22 18.73 固定权值法 28.86 11.56 21.35

表 3 3种模型实验数据对比 Table 3 Experimental data comparison of three models

从表 3可看出，在相同初始温差情况下，与另外两个模型相比，采用熵权-TOPSIS模型后，板坯平均温差分别多下降了3.71℃和5.05℃.在规格发生变化时，这种现象更为明显(见图 4).

Figure 4

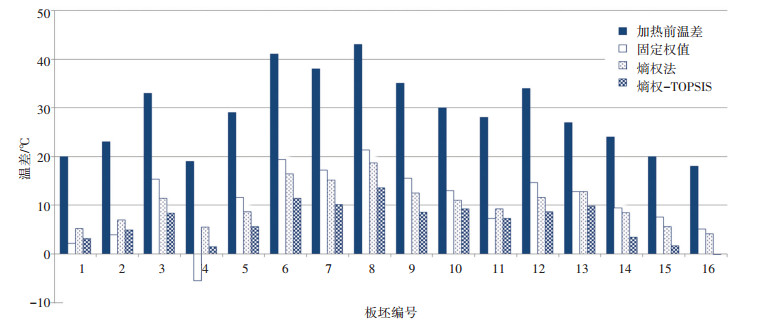
图 4 S组板坯的温差变化 Figure 4 Temperature difference of slabs in the three models

相较其他两种模型，应用本文提出的方法，规格变化时板坯温度受到的影响最小. S5、S9和S13分别为换规格后的第一块板坯：S5温差比熵权法小3.65 ℃，比固定权值法小6.18 ℃；S9温差比熵权法小4.08 ℃，比固定权值法小7.24 ℃；S13温差比熵权法小3.33 ℃，比固定权值法小3.83 ℃.

由图 4可知，板坯温差在每个模型的设定炉温下均有所下降.对于固定权值模型，由于距离出炉门最近的板坯的权值为1，所以S1和S2的温差相对较小，甚至低于熵权-TOPSIS模型; 但是随着S组板坯陆续进入控制段，对于相邻两块温度相差较大的板坯，炉温设定会产生较大的波动，从而导致升温较慢或过烧现象.对于原始熵权法模型，板坯的炉温减小量比固定权值模型要大，但是如第2节所说，熵权表示的是各指标竞争的激烈程度，而不是各指标的实际重要程度，温度和板坯位置的微小变化会导致设定值出现较大偏差，体现了此模型的不稳定性.

图 5为两种模型下的炉温设定变化情况，固定权值的模型设定值始终与距离出炉门最近的板坯所对应的炉温相同；熵权-TOPSIS法则综合了所有在控制段内的板坯数据，因此其炉温变化相对较小，其中平均炉温波动值为13.02 ℃，最大炉温波动值为51 ℃.而采用固定权值的模型平均炉温波动值为22 ℃，最大炉温波动值为59 ℃.

Figure 5

图 5 两种模型下的炉温设定值变化情况 Figure 5 The temperature setting value changes of furnace in the two models

1) 引入特殊钢种等级概念，根据板坯出炉温度要求严格性的差异，将不同钢种分成不同等级，并确定其权重, 大大增强了模型的灵活性和全面性.在炉区中板坯发生更迭时，模型进行一次计算，避免了多次计算而造成的频繁改变炉温的情况.

2) 本文模型针对单个控制段内的板坯进行计算，避免了针对所有在炉板坯进行计算时数据量过大的问题，且炉温变化较为平缓.平均炉温波动值为13.02 ℃，最大炉温波动值为51 ℃，大大低于固定权值方法所设定的炉温，也避免了固定权值模型中炉温变化量过大而影响板坯加热的效果.

3) 采用改进型熵权-TOPSIS法的在线炉温设定模型，反映了一个控制段内所有板坯的当前属性，通过对待评因素的分析确定出当前的综合炉温设定值.与固定权值模型和原始熵权模型相比，本文模型更全面地考虑加热段内的所有板坯，大幅度降低了所有板坯的温差，与固定权值法相比，其平均温差下降5.05 ℃，最大温差下降7.77 ℃.