管液压成形(tube hydroforming, THF)又叫内高压成形,是一种利用高压液体做成形介质,同时配合轴向进给使管材塑性变形成形出与模具形状相适应零件的工艺方法. THF具有强度高、零件数量少、成形精度高等一系列优点[1-2].然而,THF与传统冲压焊接工艺不一致,相应的成形工艺理论较缺乏.上世纪70年代后期,THF成形技术开始用于汽车零部件成形,此后,逐步被用于汽车及其它工业领域.
THF成形质量受管材材料参数、零件几何形状以及加载路径的影响,其中加载路径的影响最大,不恰当的工艺参数将导致零件液压成形中起皱、屈曲及破裂等缺陷. THF加载路径的优化算法主要包括基于梯度算法、进化算法等的传统方法及基于代理模型的近似优化算法.由于采用代理模型能够克服传统优化方法容易陷入局部最优以及迭代次数过大的缺陷,近年来被学者们广泛采用.所用的代理模型[3]主要有响应面法(response surface method, RSM)模型、径向基函数(radial basis function, RBF)模型、克里金(Kriging, KG)模型、人工神经网络(artificial neural network, ANN)模型及最小二乘支持向量回归机(least square support vector regression, LSSVR)模型.
Brooghani等[4]基于多级RSM进行管液压成形优化研究,将厚度方差作为优化目标,突起高度作为约束,研究结果表明厚度变化值大大改善. Abdessalem等[5]基于RSM和LSSVR进行THF多目标优化和全局灵敏度分析研究,结果表明LSSVR对于RSM在处理实际的非线性工业问题有更好的优势. Huang等[6]提出一种基于KG的非概率区间优化设计方法用于THF加载路径的优化设计,结果表明区间优化的结果更为稳健可靠. Ingarao等[7]比较了古典多项式回归方法(classical polynomial regression approach, PR),移动最小二乘近似法(moving least squares approximation, MLS)和KG方法应于THF的成形效率, 结果表明,MLS和KG可大幅度减少液压成形优化中计算工作量. Zhang等[8]提出了一种混合的方法来优化THF加载路径, 基于ANN构建代理模型, 并在专用液压成形机上进行了实验验证.
尽管基于代理模型的优化可大大减少采用梯度算法或者进化算法的优化计算求解时间,但目前绝大多数的基于代理模型的THF加载路径优化都基于静态模型.采用静态代理模型进行THF这样的高度非线性问题的加载路径最优化问题求解时,要构造整个设计域的高精度代理模型需要大量的计算样本,这势必引起计算效率降低.为了避免静态代理模型进行全局优化计算效率低的问题,学者们引入自适应优化算法,进行THF加载路径的优化设计[9-10],通过逐步缩小设计空间或者向样本库中逐步添加样本点的方法,提高关键区域的局部计算精度,进而提高所求问题的全局计算精度.该方法能在保证求解精度的前提下,提高多目标优化问题的计算效率.此外,在实际工程中,很多问题都是多目标的,因此,开展多目标代理模型优化研究与实际工程问题更一致.
本文基于LSSVR模型,进行T型THF自适应多目标优化研究.首先通过算例说明本文方法的有效性,而后将该方法用于T型THF加载路径的多目标优化设计,并将优化结果与文献[11]中的实验结果进行了对比.
1 自适应迭代LSSVR模型的多目标优化 1.1 多目标优化问题一般的多目标优化问题可以表述为
| $ \begin{array}{*{20}{c}} {\min \left\{ {{f_1}\left( x \right),{f_2}\left( x \right), \cdots ,{f_k}\left( x \right)} \right\},}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;{g_i}\left( x \right) \le 0\left( {i = 1,2, \cdots ,l} \right),}\\ {{x_{\rm{l}}} \le x \le {x_{\rm{u}}}.} \end{array} $ | (1) |
式中:f为目标函数,k为目标函数数目,gi为第i个约束函数,l约束函数数目,xl与xu分别为设计变量的下限和上限.
1.2 LSSVR模型LSSVR是一种修正的SVR模型[5],其基本表达式如下:
| $ \tilde y\left( x \right) = {\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}\left( x \right) + b. $ | (2) |
式中:φ为输入的映射函数,w与b为未知系数.通过最小二乘法与lagrangian乘数法求解,则式(2) 可以表示为式(3):
| $ \begin{array}{l} \tilde y\left( x \right) = \sum\limits_{k = 1}^N {{\alpha _k}K\left( {{x_k},x} \right) + b} ,\\ \left[ {\begin{array}{*{20}{c}} 0&{{{\vec I}^{\rm{T}}}}\\ {\vec I}&{\mathit{\Omega + }{\gamma ^{ - 1}}I} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} b\\ \mathit{\boldsymbol{\alpha }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ \mathit{\boldsymbol{y}} \end{array}} \right]. \end{array} $ | (3) |
其中y =[y1, y2, …, yn]T,α =[α1, α2, …α3]T, I为单位矩阵,γ为正则化系数,
| $ {\mathit{\Omega }_{kl}} = \mathit{\boldsymbol{\varphi }}{\left( {{x_k}} \right)^{\rm{T}}}\mathit{\boldsymbol{\varphi }}\left( {{x_{\rm{l}}}} \right) = K\left( {{x_k},{x_{\rm{l}}}} \right), $ |
K为核函数,在本文中使用RBF核函数模型
| $ K\left( {{x_k},{x_{\rm{l}}}} \right) = \exp \left( { - \frac{{{{\left\| {{x_k} - {x_{\rm{l}}}} \right\|}^2}}}{{{\sigma ^2}}}} \right). $ |
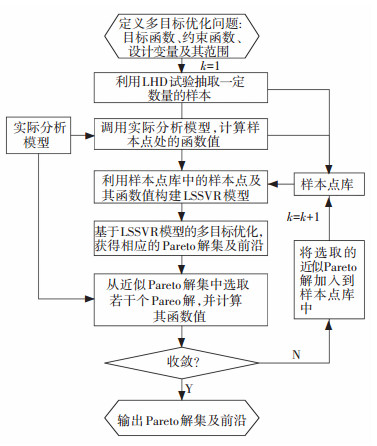
自适应迭代LSSVR多目标优化策略流程如图 1所示.
|
图 1 自适应迭代LSSVR多目标优化流程 Figure 1 The flowchart for multi-objective optimization using adaptive iteration LSSVR |
自适应迭代LSSVR多目标优化步骤:
步骤1 设置多目标优化问题,定义自变量、目标函数和约束函数,设容差ε=2%, 迭代步k=1;
步骤2 用拉丁超立方体设计(Latin Hypercube Design, LHD)获得初始采样点,调用实际模型评估的目标和约束函数值.在样本点库中保留采样点和相应的函数值;
步骤3 使用样本点库中的采样点根据式(1) 与式(2) 构建LSSVR,并应用LSSVR进行多目标优化设计.获得近似Pareto解集和Pareto前沿[12];
步骤4 从近似Pareto解集中选取若干Pareto解,并计算其函数值[13];
步骤5 当设定容差满足
| $ \begin{array}{*{20}{c}} {\varepsilon < \max \left\{ {\left| {\frac{{{f_1} - {{\tilde f}_1}}}{{{f_1}}}} \right|, \cdots ,\left| {\frac{{{f_k} - {{\tilde f}_k}}}{{{f_k}}}} \right|,} \right.}\\ {\left. {\left| {\frac{{{g_1} - {{\tilde g}_1}}}{{{g_1}}}} \right|, \cdots ,\left| {\frac{{{g_l} - {{\tilde g}_l}}}{{{g_l}}}} \right|} \right\}} \end{array} $ | (4) |
时,优化问题收敛则输出Pareto解集及前沿,否则在样本库中保留近似Pareto解及相应的函数值并转至步骤3.式(4) 中,
为了验证本文自适应迭代模型多目标优化的有效性, 选取数值算例测试函数[14]对其进行测试,函数表达式如下:
| $ \left\{ \begin{array}{l} {f_1} = 1 + \left( {{A_1} - {B_1}} \right) + {\left( {{A_2} - {B_2}} \right)^2},\\ {f_2} = \left( {{x_1} + 3} \right)2 + {\left( {{x_2} + 1} \right)^2},\\ {A_1} = 0.5\sin 1 - 2\cos 1 + \sin 2 - 1.5\cos 2,\\ {A_2} = 1.5\sin 1 - \cos 1 + 2\sin 2 - 0.5\cos 2,\\ {B_1} = 0.5\sin {x_1} - 2\cos {x_1} + \sin {x_2} - 1.5\cos {x_2},\\ {B_2} = 1.5\sin {x_1} - \cos {x_1} + 2\sin {x_2} - 0.5\cos {x_2},\\ - pi \le {x_1},{x_2} \le pi. \end{array} \right. $ | (5) |
利用遗传算法NSGA-Ⅱ[15]求解测试函数的Pareto前沿,作为测试函数的“真实解”,所选的种群数目为100,最大迭代次数200,交叉概率和变异率分别为0.8和0.2,Pareto入口比例0.4.
用LHD获得15个初始采样点,构建调用实际模型评估的目标和约束函数值.在样本点库中保留采样点和相应的函数值;
利用LHD获得15个初始采样点构建自适应LSSVR模型,利用遗传算法NSGA-Ⅱ获得代理模型的Pareto解集及前沿作为函数值的近似Pareto解及前沿,从近似解中选取3个Pareto解计算测试函数(5) 的值,经过4个迭代步获得最终的近似Pareto最优解.
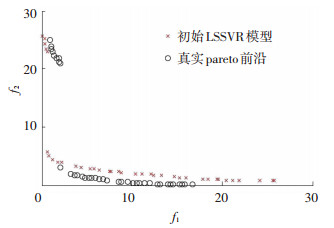
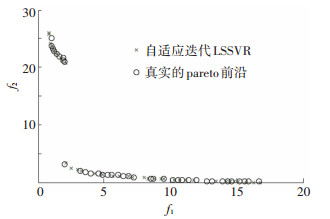
图 2为初始LSSVR模型与采用遗传算法求解的数值算例真实Pareto前沿的对比,由对比可以看出,两者存在较大的误差. 图 3为经过4个迭代步,27个样本点的自适应迭代LSSVR模型的Pareto前沿与采用遗传算法直接求解的数值算例真实Pareto前沿的对比.由对比可以看出,两者吻合得很好.对比图 2和图 3的结果可知,采用自适应LSSVR模型所获得的测试函数的Pareto前沿与采用遗传算法直接求解得到的真实Pareto前沿有较好的一致性,说明了本文方法的有效性.
|
图 2 初始LSSVR模型与函数真实Pareto前沿 Figure 2 The Pareto front obtained from initial LSSVR |
|
图 3 自适应迭代LSSVR模型与真实函数的Pareto前沿 Figure 3 The Pareto front obtained from adaptive iteration LSSVR and actual Pareto front |
假定数值算例为大型非线性工程问题,完成单次求解都要花费较长的时间.如果直接利用NSGA-Ⅱ算法进行最优化问题求解,种群数目和最大迭代次数分别100与200时,要进行100×200=20 000次耗时的工程计算,优化问题因过长的计算时间而失去意义.而采用自适应迭代LSSVR模型时,优化问题求解只需要进行27次求解就可以得到最优解,相对于直接使用NSGA-Ⅱ算法,其函数调用次数减少了99.99%,计算效率大大提高.
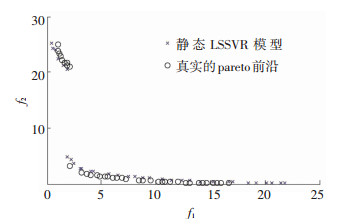
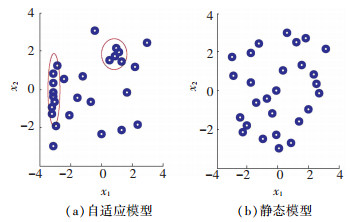
静态LSSVR模型的Pareto前沿与真实函数的Pareto前沿对比如图 4所示.由图 4可知,静态LSSVR模型没能很好地捕捉到真实函数的Pareto前沿. 图 5给出了自适应LSSVR模型与静态LSSVR模型的对比,图中红圈内给出了测试函数的真实Pareto解集的区域,对比图 5(a)与图 5(b)可知,自适应LSSVR模型在红圈内的具有更密集样本点,能够更好地捕捉到函数的真实Pareto前沿.
|
图 4 静态LSSVR模型与真实函数的Pareto前沿 Figure 4 The Pareto front obtained from one time LSSVR and actual Pareto front |
|
图 5 自适应LSSVR模型与静态LSSVR模型的样本分布 Figure 5 The distribution of sampling points of adaptive iteration LSSVR and one-time LSSVR |
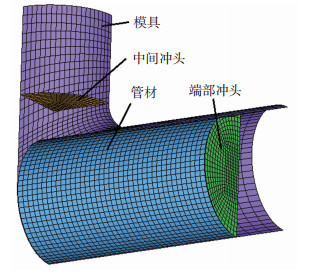
根据对称性,建立1/4 T型THF有限元模型,在对称面上施加限制其在对阵面内相对移动及转动的对称约束,使1/4模型具有与使用完整模型一致的力学特性,所建模型如图 6所示.
|
图 6 T型THF有限元模型 Figure 6 A quarter of the finite element model used for numerical simulation |
该模型包含4个部件,分别为模具、管材、端部冲头及中部背压冲头.管材单元类型为4800BT单元,模具、端部冲头及中间背压冲头为刚性单元,模型共包含5 328个节点,5 124个四边形单元.模型几何尺寸如表 1所示.管材与模具、端部冲头以及中部背压冲头之间采用单向成形面-面接触算法,摩擦因数设为0.05.
| 表 1 管材以及模具的主要参数 Table 1 The geometrical size of the tube and abrasive |
管材材料为1Cr18Ni9Ti,有效应力与有效应变之间的Swift幂指数模型[11]为
| $ \bar \sigma = K{{\bar \varepsilon }^n}. $ |
式中:K与n分别为强化系数与硬化指数,σ与ε分别为材料的有效应力与有效应变.材料用三参数塑性Barlat’s(Barlat’s 3-Parameter Plastic Model)屈服准则
| $ \begin{array}{l} f\left( \sigma \right) = a{\left| {{K_1} + {K_2}} \right|^m} + a{\left| {{K_1} - {K_2}} \right|^m} + \\ \;\;\;\;\;\;\;\;\;\;\;\;c{\left| {{K_2}} \right|^m} = 2\sigma _y^m. \end{array} $ |
| $ \begin{array}{*{20}{c}} {{K_1} = \left( {{\sigma _{11}} + h{\sigma _{22}}} \right)/2,}\\ {{K_2} = \sqrt {{{\left( {\left( {{\sigma _{11}} - h{\sigma _{22}}} \right)/2} \right)}^2} + {p^2}\sigma _{12}^2} .} \end{array} $ |
式中:σ11、σ22与σy分别为材料主平面内的主应力、切应力及初始屈服极限,a、c、h与p分别为各项异性系数R0、R45与R90所确定的参数,m的值取6.管材材料参数如表 2所示.
| 表 2 1Cr18Ni9Ti管材材料参数 Table 2 1Cr18Ni9Ti material properties |
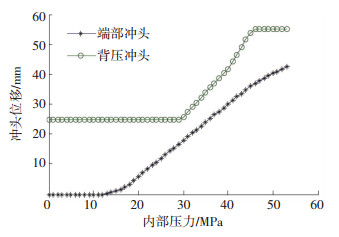
为了与试验结果对比,T型THF仿真分析的初始加载路径与文献[11]中的实验所描述的加载路径一致,加载曲线如图 7所示,内压最大值为55.00 MPa,最大轴向进给量为55.00 mm.
|
图 7 T型THF仿真与试验加载曲线 Figure 7 The loading path used for the FE simulation and experiment |
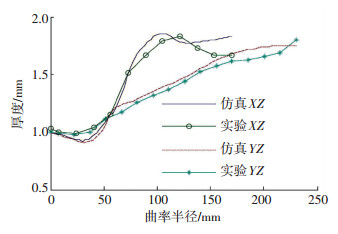
进行有限元仿真分析,有限元仿真的厚度分布与实验结果[11]在Oxz与Oyz平面的厚度分布情况如图 8所示.由图 8可知,虽然Oxz平面内管材端部厚度的有限元仿真结果与实验结果差异相对较大,但所有点的误差均在±10%以内,该有限元模型可以用于后续的加载路径的优化设计.以T型管与中央背压冲头接触面积最大及零件最大减薄率最小为优化目标,以T型管的成形高度大于实验值(55.00 mm)为约束条件进行T型THF的优化分析.
|
图 8 实验与仿真的厚度分布 Figure 8 Thickness distribution along curvilinear distance, from the tube center to tube end along x-z and y-z planes |
采用Taguchi方法[16]对屈服压力py、成形过程中的膨胀压力pe、整形压力pc、起皱开始时刻t1、突起与背压冲头接触时刻t2、轴向进给开始减少时的值D1、轴向进给停止时的值D2、轴向进给开始减少时刻t3、背压冲头初始位置S1、背压冲头最终位置S2、突起与背压冲头接触时刻t4、背压冲头停止运动时刻t5这12个设计参数进行筛选.采用L27(313)正交实验表[17]进行12个因素试验优化设计,每个因素设置为3水平,如表 3所示.
| 表 3 设计变量各参数的变化范围 Table 3 The initial ranges of the variables |
为了进一步筛选设计变量,先计算参数信噪比. Taguchi方法中使用信噪比来衡量质量偏离期望值的程度. T型THF中,管材与中央背压冲头接触面积、支管高度及最大减薄率指标可以用越大越好与越小越好指标S/N计算,如式(6) 与式(7) 所示:
| $ S/N = - 10\log \left( {y_i^2/n} \right), $ | (6) |
| $ S/N = - 10\log \left( {1/\left( {ny_i^2} \right)} \right). $ | (7) |
式中:yi为成形指标,n为单一水平下重复实验次数.信噪比均值可表示为
| $ \overline {S/N} = \frac{1}{k}\sum\limits_{i = 1}^k {{{\left( {S/N} \right)}_i}} . $ |
式中: i表示第i次实验,k为总实验次数.整体的离差表示为
| $ SS = \sum\limits_{i = 1}^k {{{\left( {\left( {\overline {S/N} } \right) - {{\left( {S/N} \right)}_i}} \right)}^2}} , $ |
第i个因素的离差平方和SSi为
| $ S{S_i} = \sum\limits_{i = 1}^k {{{\left( {{{\left( {\overline {S/N} } \right)}_{ij}} - \frac{1}{k}\sum\limits_{i = 1}^k {{{\left( {S/N} \right)}_i}} } \right)}^2}} . $ |
式中:
| $ {P_i} = S{S_i}/\left( {SS} \right) \times 100\% . $ | (8) |
根据公式(8) 计算出各参数对成形质量百分贡献比的大小, 作为筛选参数的依据,如表 4所示.根据百分贡献比选出贡献最大的参数,12个设计参数缩减为5个设计参数x =(pe, t2, t3, S2, D1)T.其他非显著性参数的取值如表 5所示.
| 表 4 各设计变量对成形质量的百分贡献比 Table 4 Analysis of variance for forming quality |
| 表 5 非显著性参数的取值 Table 5 Values of the insignificant loading parameters |
T型管的多目标优化问题的构造如下:
| $ \begin{array}{l} \min \left\{ { - f\left( x \right),{g_1}\left( x \right)} \right\},\\ {\rm{s}}{\rm{.t}}\;f\left( x \right) \ge 4014.997,\\ {g_1}\left( x \right) \le 35\% ,{g_2}\left( x \right) \ge 55,\\ {x_1} \le x \le {x_{\rm{u}}}. \end{array} $ |
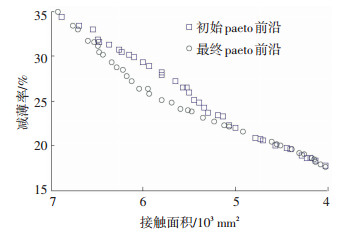
式中:f、g1与g2分别为接触面积、最大减薄率与成形高度. xl与xu的取值见表 3.依照图 1的优化流程图,设定容差ε=0.02;采用LHD获得20个初始采样点,调用有限元模型计算样本点的目标函数和约束函数值,并在样本点库中保留采样点和相应的函数值;使用样本点库中的采样点构建LSSVR模型,并应用LSSVR模型进行多目标优化设计.经过4个迭代步共32次有限元分析,迭代过程达到收敛,所得的初始Pareto前沿与最终Pareto前沿如图 9所示.
|
图 9 最终与初始Pareto前沿 Figure 9 The final and initial Pareto front |
由图 9可知,基于自适应LSSVR模型的初始Pareto前沿迭代终了的Pareto前沿在接触面大于5 500.00 mm2时与初始Pareto前沿差异较大, 说明了初始的Pareto前沿可能没有真正地捕获到实际的Pareto前沿.为了从多目标优化的多个最优点中选取合适的参考点,本文采用理想点法[12]对参考点进行筛选,数学表达式如式(9) 所示:
| $ \min D = \sqrt {\sum\limits_{i = 1}^M {{{\left( {{f_i} - {f_{i{\rm{best}}}}} \right)}^2}} } . $ | (9) |
式中:fi与fibest分别为第i个目标函数值及第i个目标函数的最优值.
利用理想点法选取获得最优妥协解时的参数值如表 6所示,此时接触面积、最大减薄率与成形高度的相对误差如表 7所示,其厚度分布云图如图 10所示.由表 7可知,自适应LSSVR模型预测结果与有限元分析结果的相对误差较小,只有最大减薄率相对误差稍大(2.58%),表明自适应LSSVR模型预测结果基本接近了实际的Pareto前沿.

|
图 10 最优妥协解的厚度分布云图 Figure 10 The thickness distribution of the most satisfactory solution |
| 表 6 最优妥协解的参数值 Table 6 Values of the most satisfactory solution |
| 表 7 最优妥协解的计算结果 Table 7 Results of the most satisfactory solution |
自适应LSSVR模型的最优妥协解与文献[11]实验结果的比较如表 8所示,在保持成形高度不变差的前提下,接触面积提高32.42%,最小厚度增加14.29%.
| 表 8 最优妥协解与实验结果对比 Table 8 Results of the most satisfactory solution and experimental result |
1) 采用自适应迭代LSSVR模型,通过逐步向样本空间增加样本点的方式提升关键区域的近似精度,显著提高多目标优化问题的全局求解精度.
2) 针对于数值算例的测试函数,采用自适应迭代LSSVR模型与直接使用NSGA-Ⅱ算法相比,函数调用次数减少了99.99%,计算效率显著提高.
3) 将自适应迭代LSSVR模型应用于T型THF加载路径的多目标优化设计,通过理想点法选择的最优妥协解与文献[11]实验值相比,在保持成形高度不变差的前提下,接触面积提高32.42%,最小厚度增加14.29%.
| [1] | AHMETOGLU M, ALTAN T. Tube hydroforming:state-of-the-art and future trends[J]. Mater Process Technol, 2000, 98(1): 25-33. DOI: 10.1016/S0924-0136(99)00302-7 |
| [2] | DOHMANN F, HARTL C H. Hydroforming: a method to manufacture lightweight parts[J]. Mater Process Technol, 1996, 60: 669-676. DOI: 10.1016/0924-0136(96)02403-X |
| [3] |
黄天仑. T型管液压成形加载路径的稳健性优化设计[D]. 长春: 吉林大学, 2016.
Huang Tianlun.The robust optimization of the loading path for t-shape Tube Hydroforming[D].Changchun: Jilin University, 2016. |
| [4] | BROOGHANI S Y A, KHALILI K, SHAHRI S E E, et al. Loading path optimization of a hydroformed part using multilevel response surface method[J]. The International Journal of Advanced Manufacturing Technology, 2014, 70(5/6/7/8): 1523-1531. |
| [5] | ABDESSALEM A B, EL-HAMI A. Global sensitivity analysis and multi-objective optimization of loading path in tube hydroforming process based on metamodeling techniques[J]. The International Journal of Advanced Manufacturing Technology, 2014, 71(5/6/7/8): 753-773. |
| [6] | HUANG T, SONG X, LIU M. A Kriging-based non-probability interval optimization of loading path in T-shape tube hydroforming[J]. The International Journal of Advanced Manufacturing Techno-logy, 2016, 85(5): 1615-1631. DOI: 10.1007/s00170-015-8034-x |
| [7] | INGARAO G, MARRETTA L, LORENZO R D. A comparison between three meta-modeling optimization approaches to design a tube hydroforming process[J]. Key Engineering Materials, 2012, 504-506: 607-612. DOI: 10.4028/www.scientific.net/KEM.504-506 |
| [8] | ZHANG Y, CHAN L, CHUN W, et al. Optimization for loading paths of tube hydroforming using a hybrid method[J]. Materials and Manufacturing processes, 2009, 24(6): 700-708. DOI: 10.1080/10426910902769392 |
| [9] | WANG G, DONG Z, AITCHISON P. Adaptive response surface method: a global optimization scheme for approximation-based design problems[J]. Engineering Optimization, 2001, 33(6): 707-734. DOI: 10.1080/03052150108940940 |
| [10] | WANG G. Adaptive response surface method using inherited latin hypercube design points[J]. Journal of Mechanical Design, 2003, 125(2): 210-220. DOI: 10.1115/1.1561044 |
| [11] |
李凯. T型三通管液压成形加载路径优化[D]. 哈尔滨: 哈尔滨工业大学, 2010.
LI Kai. T-shape tube hydroforming optimal design of loading pass[D].Harbin: Harbin Institute of Technology, 2010. |
| [12] |
孙靖明, 梁迎春.
机械优化设计[M]. 北京: 机械工业出版社, 2012.
SUN Jingming, LIANG Yingchun. Optimal Design of Machine[M]. Beijing: China Machine Press, 2012. |
| [13] |
韩岩, 李晓. 加速大数据聚类K-means算法的改进[J].
计算机工程与设计, 2015, 36(5): 1317-1320.
HAN Yan, LI Xiao. Improved accelerating large data K-means clustering algorithm[J]. Beijing: Compute Engineering and Design, 2015, 36(5): 1317-1320. |
| [14] | DEB K. Multi-objective optimization using evolution aryalgorithms[M]. Hoboken: John Wiley & Sons, 2001. |
| [15] | DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. DOI: 10.1109/4235.996017 |
| [16] |
李忠范, 高文森.
数理统计与随机过程[M]. 北京: 高等教育出版社, 2000.
LI Zhongfan, GAO Wensen. Mathematical statistics and stochastic process[M]. Beijing: Higher Education Press, 2000. |
| [17] |
任露泉.
试验优化设计与分析[M]. 长春: 吉林科学技术出版社, 2001.
REN Luquan. Optimum design and analysis of experiments[M]. Changchun: Jilin Science and Technology Press, 2001. |
 2017, Vol. 49
2017, Vol. 49


