一次二阶矩法、二次可靠性方法、Monte Carlo方法^[1]等广泛应用于可靠性分析中.但是, 一次二阶矩方法、二次可靠性方法等只适用于显式功能函数，而对于工程问题，大多数情况下功能函数是隐式函数，这时可以应用数值模拟的方法进行分析.基于数值模拟的可靠性分析方法如Monte Carlo方法是求解失效概率直观、精确的一种方法，但是它需要大量的随机样本，无法在短时间内进行可靠性评估.代理模型的方法在一定程度上解决了这类隐式可靠性分析问题，如响应面法^[2-6]、人工神经网络方法^[6-7]、支持向量机、Kriging方法等^[8-12]. Kriging模型作为一种新的代理模型，最初应用于地质统计学中，现在，它被应用在可靠性评估中. Kriging方法最大的特点是不需要建立一个特定的数学模型，即是一种包含了多项式和变差函数的模型，避免了只有多项式模型对结构可靠度计算精度的影响.近十几年，Kriging方法在工程领域得到了广泛应用^[13].

由于Kriging模型采用Gaussian随机过程模拟，样本集Ω在构造Kriging预测模型过程中发挥重要作用，Ω的构成对$\hat G(x)$精度有很大影响.通常情况下，增加Ω中样本点数有益于降低代理模型误差，改善${\hat P_{\rm{f}}}$准确性；然而，样本点数过多会同时增加有限元数值仿真及Monte Carlo方法近似计算P_f的计算量.因此，需要一种高效抽取样本点的方法，在控制Ω样本点数情况下得到足够精度的代理模型及${\hat P_{\rm{f}}}$.为此，学者提出学习函数帮助提高抽取样本的效率.

基于Kriging模型的学习函数中，应用最广泛的是Bichon等^[14]提出的EFF(Expected Feasibility Function)函数及Echard等^[15-16]提出的U函数. EFF函数能够用来度量点x落在真实极限状态函数G(x)=0附近的期望，而U函数是点x系统响应被错误分类可能性的度量. EFF和U在输入变量X维数不高情况下效率很高，随着维数的增加效率会逐渐降低，因此，不适合用于多维情况的可靠性分析中.

本文基于Kriging模型，根据现有模型的不足，考虑联合概率密度函数对失效概率预测准确性的影响，提出了一种新的学习函数及相应的学习停止条件，将学习函数和学习停止方法与Monte Carlo方法相结合, 提出一种新学习方法，并通过两个例子对几种学习方法进行比较.

Kriging模型是一种高效的插值方法，包含确定性和随机两个部分，确定性部分一般采用最小二乘多项式拟合，随机部分为高斯过程.以最小方差无偏估计保证差值精度，通过最大似然法或交叉验证法确定高斯过程相关性参数.

Kriging模型假设功能函数G(x)可表示为

式中: g(x)=[g₁(x), …, g_p(x)]^T是定义在输入变量X空间内的基函数，β =[β₁, …, β_p]^T为与g (x)对应的回归系数.本文中暂定g (x)为一次多项式.式(1) 中z(x)为零均值同方差高斯过程，z(x_i)、z(x_j)的协方差为

式中：σ²是高斯过程的方差. R(x_i, x_j; θ)表示z(x_i)和z(x_j)的相关系数，θ是相关函数R(x_i, x_j; θ)的参数.目前应用最广泛的是高斯相关函数:

其中，x_i^m表示向量x_i的第m个元素.

若已知样本集

式(1)~(3) 中未知参数β、σ²、θ可通过极大似然法估计得到，

式中：

分别用$\boldsymbol{\hat \theta }, \boldsymbol{\hat \beta }, {\hat \sigma ^2}$表示θ、β、σ²的极大似然估计值.点x的Kriging预测值可表示为Y的线性组合形式，

结合式(1)、(4) 的估计误差为

式中：Z =(z₁, z₂, …, z_N)^T.要实现$\hat G(\boldsymbol{x})$的最小方差无偏性^[11]，则c (x)需满足，

求式(5) 的最优解可得$\hat G(\boldsymbol{x})$的Kriging表达式为

式中:

X的联合概率密度函数为f(x)，不失一般性，本文中假设X服从M维正态分布.功能函数G(x)将X空间分为两部分，即安全域S_s={x | G(x)>0, x∈R^M}和失效域S_f={ x | G(x)≤0, x∈R^M}.则失效概率为

由样本集Ω得到的Kriging预测模型$\hat G(\boldsymbol{x})$估计失效概率P_f值为

Monte Carlo方法，以大数定律为理论基础，通过随机抽样以随机样本失效频率估计失效概率，当随机样本N_MC足够大时，能够得到足够精度的${\hat P_{\rm{f}}}$值.在计算量处于可以接受情况下，Monte Carlo方法是鲁棒性最强随机抽样方法.因此本文中采用Monte Carlo方法近似计算${\hat P_{\rm{f}}}$:

式中:I_f(·)是失效域指示函数，通常表示为

${\hat P_{\rm{f}}}$的变异系数表示为

目前，确定样本集Ω的方法可分为两类：

1) 随机抽样法.该方法主要是首先给定Ω中样本量N₀，采用Monte Carlo、拉丁超立方等随机抽样方法确定Ω.此类方法简单易懂，操作方便，但效率低，容易造成样本点浪费.特别是输入变量数维数较大时无法保证Ω中各点均匀分布在变量空间内.

2) 连续抽样法.此类方法首先通过随机抽样确定初始样本Ω₀，根据Ω₀构造初始代理模型；再根据初始模型提供的统计信息构造“学习函数”，在输入变量空间或给定样本中寻找学习函数的最大值点或最小值点，将其加入Ω₀中，重新构造代理模型.重复以上过程，直至代理模型或${\hat P_{\rm{f}}}$满足一定条件.该类方法中，构造恰当的学习函数能够明显加快算法的收敛速度.本文基于第2种方法，提出一种新的学习函数.

由式${P_{\rm{f}}}{\rm{ = }}\int_{G(\boldsymbol{x}) \le 0} {f(\boldsymbol{x}){\rm{d}}\boldsymbol{x}} $可知，结构失效概率估计值${\hat P_{\rm{f}}}$的精度取决于$\hat G(\boldsymbol{x}) = 0$与G(x)=0间的“距离”，在$G(\boldsymbol{x}) \ne 0$的区域，只要\[\hat G(\boldsymbol{x})\]与G(x)的符号相同，就不会对${\hat P_{\rm{f}}}$的精度产生影响，当$\hat G(\boldsymbol{x}) = 0$与G(x)=0完全重合时，${\hat P_{\rm{f}}}$=P_f.因此，本文中提出在$\hat G(\boldsymbol{x}) = 0$上选取具有“代表性的”点，计算这些点的结构相应值，更新$\hat G(\boldsymbol{x}) = 0$，在迭代过程中使$\hat G(\boldsymbol{x}) = 0$逐渐接近G(x)=0直至满足收敛条件.

Echard B提出如下U函数：

U的值越小，点x符号预测错误的概率越大，如果点x在Kriging预测的曲线$\hat G(\boldsymbol{x}) = 0$上，则该点符号预测错误的概率最大(为50%).这时，|μ_G(x)|=0，则σ_G(x)越大，点x符号预测错误的概率越大. G(x)的概率密度函数f_G(x)是x点对失效概率影响的大小的重要判断依据. f_G(x)越大，点x对失效概率的影响越大.因此，本文中将这两个指标相结合，提出一种新的学习函数VF，且

其中f_G(x)是概率密度函数.

根据文献[12, 15]，用P_R=Φ(U)表示点x符号预测正确的概率，则P_W=Φ(-U)表示该点符号预测错误的概率. AK-MCS/AK-IS的学习停止条件是U_min>U_T，其中，Φ(U_T)=0.997，U_T=2.

但是这种学习停止条件过于严格，增加不必要的迭代次数.然而，一次计算中，样本点中符号预测的不确定性与${\hat P_{\rm{f}}}$的许用误差有关，因此提出一种新的学习停止条件，表达式为

式中:用N_{U < P}表明点x的符号的错误概率高，这样的点作为抽样中一定失效的点. N_P≤U≤Q表明点x的符号的错误概率较高，这样的点可用N_P≤U≤Q·Φ(-U)表明其失效的可能性. α是${\hat P_{\rm{f}}}$的许用误差，在一次抽样中，失效概率的计算方法为

如果符号的错误点与失效点相比非常少，就可以确定失效概率的计算是准确的.

本文中，P=1，Q=2，α=0.03.

提出的选取样本点方法的主要步骤为：

步骤1 应用拉丁超立方抽样方法随机产生初始样本点X_DoE=[x¹, x², …, x^N].

步骤2 用真实的G(x)计算Y_DoE.

步骤3 用X_DoE和Y_DoE建立Kriging预测模型，这里用到的工具是MATLAB中的DACE工具箱.

步骤4 用Monte Carlo方法生成样本空间X =[x¹, x², …, x^MC]，计算失效概率${\hat P_{\rm{f}}}$和变异系数, 变异系数的计算方法为式(6).如果变异系数δ_pf < [δ]，转到下一步，否则扩大样本空间X继续计算.

步骤5 在变异系数满足条件时计算N_u/N_f.

步骤6 如果N_u/N_f的值满足学习停止条件见式(7)，结束学习过程，否则转到下一步.

步骤7 通过Monte Carlo方法在$\hat G(\boldsymbol{x}) = 0$上抽取K个点.由于这样实现非常困难，给定U < 0.03, 计算点x的U值，当点满足U < 0.03，即认为点在$\hat G(\boldsymbol{x}) = 0$上.计算K个点的VF值，取得到最大值的点加入到样本空间X_DoE中，更新样本空间，转到步骤3建立新的Kriging预测模型.

这是一个2维随机变量小失效概率的例子, 选自文献[17]，功能函数如下：

其中:x₁、x₂服从正态分布，且相互独立. μ_x1=38，σ_x1=3.8，μ_x2=54，σ_x2=2.7.算例结果见表 1.

表 1

表 1 二维模型算例结果 Table 1 Results of example with 2-dimension 方法 Ncall ${\hat P_{\rm{f}}}$/10-3 δPf /% εPf /% MCS 3×105 6.303 2.29 - ABC-Kriging 36 6.500 2.43 3.13 AK-SSIS 9 6.303 2.29 < 0.1 4+4 6.3 0.42 < 0.1 Proposed method 4+6 6.3 0.43 < 0.1 4+4 6.3 0.43 < 0.1 4+6 6.3 0.43 < 0.1

表 1 二维模型算例结果 Table 1 Results of example with 2-dimension

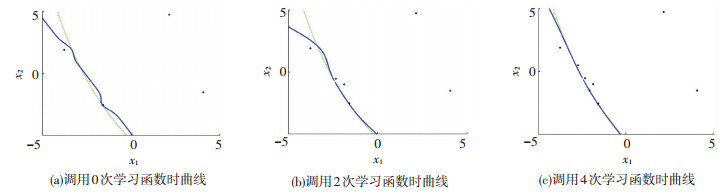
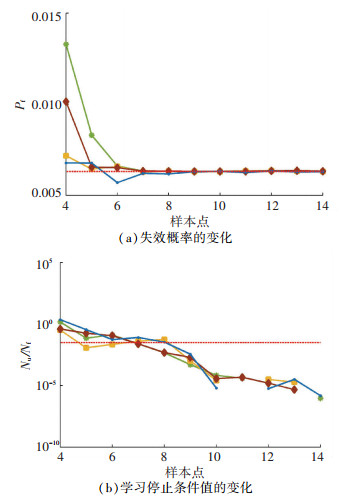
根据本文算法流程编制MATLAB程序，首先用拉丁超立方的方法选择4个初始样本点，建立Kriging模型，通过主动学习，更新初始的样本空间，重新建立了新的Kriging模型.本算例在调用学习函数4次时，到达学习停止条件.由于本算法使用较少的样本空间，因此有较好的效率，在进行4次运算时，样本空间数量少且稳定，得到的失效概率也非常一致，从而证明了本文提出的算法有较高的稳定性. 图 1描述了不同的调用次数时Kriging拟合的功能函数与真实的功能函数的匹配情况，如图 1(c)所示在调用学习函数4次时，两条曲线基本重合. 图 2(a)描述了在调用学习函数过程中失效概率的变化. 图 2(b)描述了在调用学习函数过程中学习停止条件值的变化.从图 2中可以看出, 学习停止条件到达时，失效概率刚好收敛，可见本文提出的学习停止条件是实用的.

Figure 1

图 1 预测极限状态的收敛情况 Figure 1 The convergence procedure of predicted limit state

Figure 2

图 2 初始样本点为4时失效概率和学习停止条件折线图 Figure 2 Broken line graph of ${\hat P_{\rm{f}}}$ and Nu/Nf with initial DoE=4

6维随机变量非线性系统例子见文献[2-3, 7-8, 15]，系统如图 3所示，功能函数如下：

Figure 3

图 3 非线性系统 Figure 3 Nonlinear system

式中${\omega _0} = \sqrt {({C_1} + {C_2})/M} $.各变量的分布参数见表 2.

表 2

表 2 变量分布信息 Table 2 Information of random variables 变量 分布 均值 标准差 C1 正常 1.0 0.1 C2 正常 0.10 0.01 M 正常 1.00 0.05 R 正常 0.50 0.05 T1 正常 1.0 0.2 F1 正常 0.450 0.075

表 2 变量分布信息 Table 2 Information of random variables

首先, 用拉丁超立方的方法选择15个初始样本点，建立Kriging模型，通过主动学习，更新初始的样本空间，重新建立了新的Kriging模型.本算例进行4次计算，结果列于表 3和图 4.与其他方法相比，本文提出的方法需要更少的迭代步骤，且具有较高的稳定性.

Figure 4

图 4 初始样本点=15时失效概率和学习停止条件折线图 Figure 4 Broken line graph of ${\hat P_{\rm{f}}}$ and Nu/Nf with initial DoE=15

表 3

表 3 六维模型算例结果 Table 3 Results of example with 6-dimension 方法 Ncall ${\hat P_{\rm{f}}}$/10-2 δPf/% εPf/% MCS 7×104 2.834 2.20 - AK-MCS+U 58 2.834 2.20 < 0.10 AK-IS+U 29+38 1.530 2.70 -46.01 AK-SSIS+U 29+27 1.540 2.59 -45.60 AK-MCS+EFF 56 2.850 2.20 0.16 10+38 2.860 0.59 0.92 15+37 2.830 0.59 -0.14 15+30 2.840 0.59 0.21 Proposed method 15+32 2.900 0.59 2.33 15+34 2.850 0.59 0.56 20+31 2.870 0.59 1.27

表 3 六维模型算例结果 Table 3 Results of example with 6-dimension

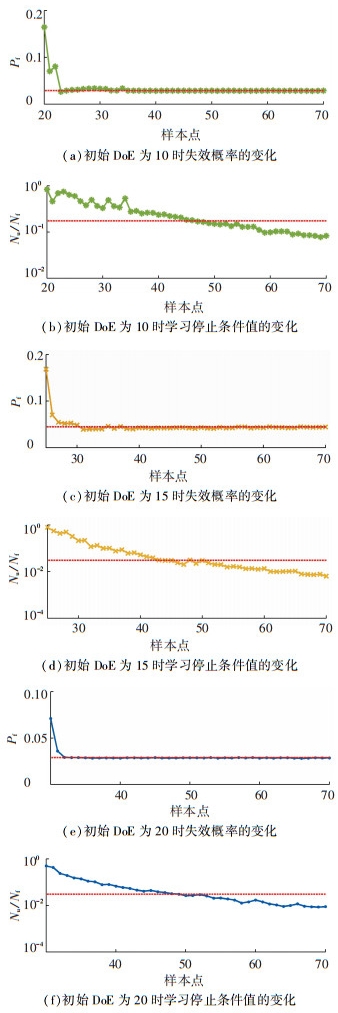
然后, 分别用用拉丁超立方的方法选择10和20个初始样本点，计算结果列于表 3和图 5. 图 5描述了在不同数量的初始样本空间时，函数的收敛情况.由图 5可见, 初始样本空间的数量对收敛数度有一定的影响，但是影响不大，且都在样本数为50左右收敛.

Figure 5

图 5 不同初始样本点时失效概率和学习停止条件折线图 Figure 5 Broken line graph of ${\hat P_{\rm{f}}}$ and Nu/Nf with different initial DoE

1) 本文利用Kriging随机特性，结合现有学习函数的不足，提出了一种新的学习函数VF，该方法将方差与联合概率密度函数相结合，提高选点的效率和稳定性.

2) 提出一种学习停止条件，既能保证失效概率计算的准确性，又不至于过于严格而造成不必要的迭代.并结合学习函数VF提出一种学习选点方法.

3) 数值算例计算结果表明，本文提出的学习方法具有较高的效率，稳定性和精度.

4) 本文方法在建模迭代过程中没有对结构功能函数线性、非线性形式，及隐式、显式情况做特定假设，因此，理论上该方法能够应用于工程中隐式且非线性程度较高情况.