产品质量是关系到企业市场竞争能力的重要指标.在生产加工技术飞速发展的今天, 质量问题依然是企业不可忽视的重要部分.在生产过程中为及时准确定位问题所在, 采取适当措施恢复生产, 不少学者利用数学模型结合领域知识展开研究，尤其针对信息完备情况下的质量特性识别^[1]、工序质量诊断^[2]以及误差控制^[3]等.由于生产过程中工艺的复杂性和小批量生产模式的使用，导致无法搜集到足够的信息建立质量问题发生的机理数学模型或借助统计方法描述演变路径, 只能通过专业人员根据以往类似问题的处理经验提出解决方案.这种过程缺乏系统性且过重依赖于人的头脑，一旦人员流失，积累的经验知识便再无法有效地继承和重用.因此，需要一种方法对过去的经验知识进行系统的梳理和储存，以便遇到类似问题时及时有效地进行知识重用和共享. Roger Schank于1982年提出了基于知识的问题学习和求解方法——案例推理(case-based reasoning，CBR).该方法将过去积累的经验以案例的形式储存在案例库中，根据索引策略、匹配算法以及相似度计算，从案例库中检索相似案例，经由适配策略修正，获得适合当前问题的解决方案.文献[4]将CBR应用于面向服务的价值链设计，文献[5]则结合CBR对竖炉的状态进行了相对准确的持续预测；在机械领域方面，文献[6]进行了面向夹具设计的实例检索研究，文献[7]采用模糊相似优先比算法进行卧式数控机床相似实例的检索.目前，尚鲜有关于质量问题诊断方面的研究，究其原因主要有以下两个方面：1) 缺乏定性与定量相结合的问题描述与知识表达方法；2) 缺乏高效的实例检索方法，尤其对案例库达到一定规模时的复杂问题推理.

本文引入可拓学理论中的物元模型进行实例知识表达，在领域知识索引下构建分层案例库，通过可拓推理实现案例的检索、重用、修正以及存储.

可拓学^[8]基本思想为：变矛盾问题为相容问题, 使目标问题得到解决.物元是可拓理论的基本逻辑单元，由有序三元组R=(N, c, v)表示，其中N为描述对象，c和v分别为特征项和对应的特征量值. n维物元可表示为

在案例推理中利用物元进行知识表达，可以把实例、相应特征项以及特征值集中在知识物元中统一表达，形成定性与定量相结合的表示方式.一般案例知识的构成A={IP, J, S, F }，其中IP为源案例的标识符；J为检索信息；S与F分别为解决方案与实施结果.物元知识表示中，以N作为案例标识符，特征项c = J ∪ S ∪ F，结合文献[9]所提出的特征元M =(c, v)，案例知识库可表示如下：

目标案例模型

式中G为目标案例的可拓描述，L为源案例N与目标案例N_G的相似性衡量，ρ为相似量值.

可拓学对问题的分析^[10]一般首先根据领域知识确定问题物元模型；然后根据上下文信息推导出尚未被发现的事实.在推理过程中，首先结合可拓知识对目标案例进行描述，然后利用其特征元检索源案例库，获得解决方案.用产生式规则If-Then结构可描述如下：若N_i∈CASE，N_j为目标案例,

其中S_1-k和S_(k+1)-h分别为特征项c_J和c_S的判断域.如果If为真，Then对目标案例N_j成立.

定义1 若设R为目标物元，r为条件物元，给定问题P= R * r.如果在条件r下，目标物元R不能实现，则成P为不相容问题，记为P= R ↑ r，否则为相容问题，记为P= R ↓ r.

定义2 如果某种操作可以使物元变换，则称该操作为可拓算子, 即若存在T₁X₁=Y₁，T₂Y₁=Y₂，…，T_nY_n-1=Y_n，则称T₁, T₂, …T_n为可拓算子；同时，若TX₁=Y_n成立，则可拓算子$T = \prod\limits_{i = 1}^n {{T_i}} $.

当上下文信息或现实条件r无法使目标物元R实现时，可通过可拓算子将矛盾问题调整为相容问题，途经有以下3种：1) 调整目标问题：P=(T_R: C_J)↓ r；2) 改变条件属性P= R ↓(T_r: r)；3) 前两者结合P=(T_R: C_J)↓(T_r: r).

如图 1所示，案例推理分为案例检索(Retrieve，R)、重用(Ruse，R)、修正(Revise，R)以及存储(Retain，R)4个环节，也称为4^R模型^[11].

Figure 1

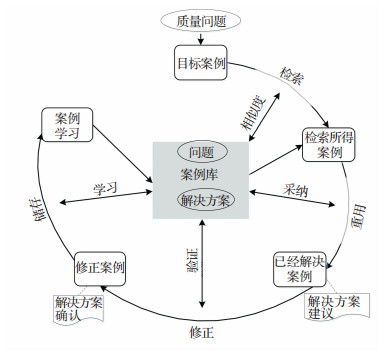
图 1 案例推理的4R模型型[11] Figure 1 4R model of case-based reasoning

1) 案例检索.从案例库中检索与目标案例相似的源案例.检索的主要步骤：

Step 1 目标案例描述.由于描述的精确程度直接影响检索结果的成败，需要通过可拓变换P= R ↑ r ⇒P=(T:c_J)↑r⇒P= R^′↓ r不断地对目标案例的特征描述进行调整，其中可拓算子T={T₁, T₂, T₃, T₄}={置换，增删，分解，扩缩}.

Step 2 根据目标案例特征元检索相似源案例.鉴于各检索特征项对最终相似度影响程度的不同，首先确立其影响权值w，然后进行目标案例与源案例的相似性衡量.

Step 3 根据判断阈值δ确定检索结果.检索终止于如下3种情况：(1) 检索到ρ_i≥δ，(i=1, 2, …, n)的若干源案例，得到相似案例解集，此为理想情况；(2) 遍历案例库后，∀ρ_i＜δ(i=1, 2, …, n)，则返回Step 1；(3) 若仍无法检索得到相似源案例，则根据专家意见对目标案例进行人为诊断，并对不断试错所得最终解决方案，以新案例的形式补充到案例库中.

2) 案例重用.将检索所得源案例的解集特征元映射至目标案例，即通过可拓传导变换T(M_N)⇒M_G实现案例重用.

3) 案例修正.对由重用案例集得到的解集特征元，根据目标案例的领域知识和相关具体工况记录进行可拓调整，优化解决方案.

4) 案例存储.目标问题得到解决后，若形成了一个可用于将来与之相似问题参考解决的源案例，则需将其存储进案例库中.

根据产品工艺结构自顶向下展开：产品物元R_d= (d, c_d, v_d)、组件物元R_e=(e, c_e, v_e)、零件物元R_q=(q, c_q, v_q)，其中：1) d=e₁⊕e₂⊕…⊕e_i, 2) e=q₁⊕q₂⊕…⊕q_j, 过程作为生产的基本单元，若过程物元R_b=(b, c_b, v_b)，则3) q=b₁⊕b₂⊕…⊕b_k.

由1)~3) 得质量问题P= R_b↓(T_r: r)，其中条件物元r = < m₁, m₂, m₃, m₄, m₅, e>，m_1-5与e分别为过程影响因素(人、机、料、法、环、测，即5M1E).结合文献[12]可得

式中R_d为产品物元，r为映射输入域，T为可拓算子.

假设工艺目标为${\boldsymbol{\tilde R}_{\rm{g}}}$，则矛盾问题为$\Delta \boldsymbol{R} = {\boldsymbol{\tilde R}_{\rm{g}}}-\boldsymbol{R}$.此时需要调整条件物元r使Δ_minR.因此根据极值定理对案例推理所得解进行评估, 得到目标案例物元模型的M_F

可拓理论提供了分析和解决矛盾问题的思维机制，通过可拓知识表达以及可拓变换推理虽已揭示了问题的本质及解决的思路，但尚缺乏解决工程技术领域问题的具体运算方法^[13].

以产品工艺结构为载体，以质量特征为核心，以工序活动衔接演化为线索对CBR要素组织的结果见图 2.

Figure 2

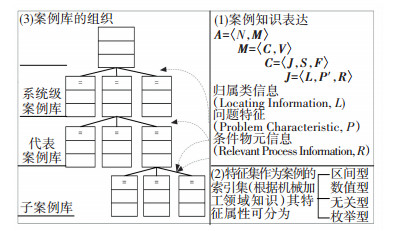
图 2 案例推理组织示意 Figure 2 Case-based reasoning organization diagram

检索特征项：c_J={ c_L, c_P′, c_R}//归属类信息，问题特征描述，相关工况条件信息//.

其中：归属类包括发现工序、产品结构子系统归属、该子系统各相关工序或活动；问题特征信息主要指问题特性和具体特征属性描述；工况类信息主要指各相关工序编号、定位基准、加工参数、加工结果等.

质量问题案例库主要源于生产过程中已解决问题的收集、整理和知识存储.随着时间的积累和加工工艺的日渐复杂，案例库的规模迅速膨胀.若检索过程采用并行处理方式直接遍历，会影响检索的效率和效果.在故障诊断的相关应用研究中，一般采用确立优先规则的方法提高检索效率.例如文献[14]以故障征兆权值和历史成功检索次数为依据进行检索优先级的确定.由于质量问题诊断的参考依据是领域知识和具体工况信息，但不同品种间历史成功检索次数的可借鉴性不高.为此，根据文献[15]提出的知识库结构有助于案例检索的观点，本文结合基于领域知识的分层案例组织形式, 将原始案例库分为系统案例库、代表案例库和子案例库3层，如图 2所示.其中代表案例库为抽象层，子案例库属于具体层.检索时，首先, 通过归属类特征元定位质量问题的系统级归属; 然后, 根据问题描述特征元检索最相似的代表案例; 最后, 在与代表案例相关的子案例库中通过问题描述和相关工况条件信息特征元进行进一步的检索.

根据同一聚类中的对象具有较高的相似度，而不同聚类中的对象差别较大的原则，把源案例库划分成一组聚类

其中t为代表案例目标聚类数.设聚类的目标函数为

式中: n为案例库中的案例总数目，z_p为第p(p=1, 2, …, t, t < n)个聚类的中心，d(x_i, z_p)为x_i到z_p的加权欧氏距离. U =[u_ip]_n×t为隶属矩阵，通过数次迭代得到一组聚类中心{z_p|1≤p≤t, p∈n}和隶属矩阵U，使得目标函数f_t最小.对于每条案例：

1)u_ip∈[0, 1], 即属于或不属于某一个聚类，二者必居其一；

2)$\sum\limits_{p = 1}^t {{u_{ip}} = 1} $，即每条案例只属于一个聚类；

3)$\sum\limits_{i = 1}^n {{u_{ip}} > 0} $, 即每个聚类都是非空的.

由于质量问题发生机理的模糊性以及相关指标的不确定性，加上处理人员领域知识和经验的局限性，难以对每个指标给出确定性的判断，故在此引入三角模糊数a_ij=(a_ij^l, a_ij^m, a_ij^u)表达判断信息，a_ij^l、a_ij^m、a_ij^u分别表示质量问题相关人员给出的目标物元特征项i与j比较后的保守、最可能以及乐观评价结果.

A =(a_ij)_m×m为形成的三角模糊判断矩阵.将A的行进行归一化得到排序权向量

其中：

由w_i=(w_i^l, w_i^m, w_i^u)，w_j=(w_j^l, w_j^m, w_j^u)为任意两个三角模糊权向量，则w_i≥ w_j的可能度为

对于w =(w₁, w₂, …, w_i, …, w_m)，任一w_i≥ w_j(i≠j)的可能度：

则排序权向量

经归一化处理,

基于上述分析，结合表 1不同数据类型特征项的局部相似度, 可得目标案例与各源案例的相似度为

表 1

表 1 局部相似度 Table 1 Local similarity 特征项类型 特征量 局部相似度 cA、cB为区间类[16] vA=[a1, a2] vB=[b1, b2] 若区间长度用L|·|表示，则 $si{m_i}({c_A}, {c_B}) = {\left[ {\frac{{{{\left| {L({v_A} \cap {v_B})} \right|}^2}}}{{\left| {L({v_A})} \right|\left| {L({v_B})} \right|}}} \right]^{1/2}}$ cA、cB为数值类 目标域[max(vi), min(vi)], i=1, 2, …, k vA∈[max(vi), min(vi)] vB∈[max(vi), min(vi)] $si{m_i}({c_A}, {c_B}) = 1 -\frac{{\left| {{v_A} -{v_B}} \right|}}{{\max ({v_i}) -min({v_i})}}$ cA、cB为无关类 vA=vB或vA≠vB $si{m_i}({c_A}, {c_B}) = \left\{ \begin{array}{l} 1, {v_A} = {v_B}时\\ 0, {v_A} \ne {v_B}时\end{array} \right.$ cA、cB为枚举类 若枚举类特征的最大赋值用K表示，则 vA或vB取值为[1, K]内整数 $si{m_i}({c_A}, {c_B}) = 1 -\frac{{\left| {{v_A} -{v_B}} \right|}}{K}$

表 1 局部相似度 Table 1 Local similarity

以某批次608-2RS球轴承在成品抽样时检测出的振动问题为例，结合2004年以来累积的深沟球轴承类的78例质量问题(信息文档记录)形成源案例库，具体检索步骤如下：

Step 1 识别目标案例. 1) 振动问题(P)=轴承(R)↑工艺条件(r); 2) 映射R_d=T(r)=T(m₁, m₂, …, m₅, e, ); 3) 寻求使P= R ↓ r的可拓算子T.

Step 2 根据归属类特征元检索系统层案例库.

1) 以初始归属类物元M_L进行检索

定位结论为内、外圈以及装配工艺，显然范围太广；

2) 对目标问题归属类特征项c_L进行增补可拓变换P= R ↑ r ⇒P=(T: c_L)↑ r ⇒P= R^′↓ r，调整c_L^′= c_L∪ c_内圈工艺∪ c_外圈工艺∪ c_装配工艺；

3) 检索，定位结论为内圈.

Step 3 问题特征物元M_P′与内圈-磨削案例库中的各代表案例进行匹配，定位为内圈圆度超差问题；其中问题特征物元M_P′为

检索过程中，根据阈值和人为判断检索结果未达到满意之前，需要不断地对检索特征元利用可拓算子进行置换、增删以及分解等调整.

Step 4 根据内圈磨削相关工艺和问题特征信息特征元对所有深沟球轴承圆度超差问题进行案例检索，得608-2RS球轴承振动问题检索的近似案例结果L= < (N, ρ)>；其中内圈磨削相关工艺信息特征元为

以上各物元特征项的权重评估源自品管和生产部门相关人员结合实际给出的保守、最可能以及乐观判断.

Step 5 根据领域知识和相关具体执行情况记录对所得解决措施进行调整.

取阈值δ=90%，得表 2所示可重用案例集.

表 2

表 2 可重用案例集 Table 2 Reusable case set 序号 节点 型号 相似度/% 1 20071001229 608Z深沟球轴承 96.25 2 20060203526 6305Z深沟球轴承 92.35 3 20060105385 6305Z深沟球轴承 90.12

表 2 可重用案例集 Table 2 Reusable case set

根据可重用案例的解决方案，通过可拓调整得到目标案例解决措施特征元，如表 3所示.

表 3

表 3 目标案例解决措施特征元 Table 3 Solution for target case Ms 措施 内容 临时措施 ① 缩短砂轮修整间隔； ② 延长超精工序时长. 长期措施 ① 临时措施作为日常辅备；② 加强套圈材料检测；③ 加强供应商管理.

表 3 目标案例解决措施特征元 Table 3 Solution for target case

由于轴承工艺结构相对简单，内圈方面的质量问题类型较为集中，在该案例推理过程中遍历检索与分层检索区别不是很显著.为进一步说明基于可拓知识的不同特征项表达与分层检索研究的意义，将其与传统案例检索做了如表 4所示的对比分析.

表 4

表 4 对比分析 Table 4 Comparative analysis 类型 检索方式 检索时间复杂度 适用范围 限制 基于可拓知识表达的分层检索 不同物元特征项分层检索 $O(\sum\limits_{j = 1}^{{n_1}} L + \sum\limits_{j = 1}^t {P'} + \sum\limits_{j = 1}^{{n_2}} R)$ 其中: k=L+P′+R; n1为各系统级案例库定位特征项数量；t为代表案例聚类数目；n2为具体案例库案例数量值. ① 特征项明确、清晰，引导动态和有方向地检索；② 适用于工艺结构繁杂且案例库规模较大. ① 归纳分析时间复杂度高； ② 对综合性、整体性问题检索效果不佳. 传统案例检索 整体特征项全局遍历 $O(\sum\limits_{j = 1}^n k)$ 其中n为案例库案例数值. ① 目标案例特征界定模糊； ② 适用于案例库规模小. ① 遍历时间复杂度高； ② 整体特征项检索，结果显著度不高.

表 4 对比分析 Table 4 Comparative analysis

1) 针对质量问题案例的形式化表示存在的局限性，本文将可拓理论与案例推理相结合，给出了基于物元模型的知识表达结构；

2) 通过可拓算子实现了对质量问题特征项在多级索引结构上的相容性求解；

3) 结合基于领域知识的分层案例组织形式与最近邻检索策略实现了608-2RS深沟球轴承振动问题的求解.