目前，已经有很多学者对单一产品、不考虑换模时间等因素的单机单作业多订单(multi-order-per-job，MOPJ)问题提出了多种调度方法.文献[1]对单一产品且不考虑其他因素的理想化单机MOPJ调度模型采用禁忌搜索算法进行了简单的研究.文献[2]对理想化单机MOPJ问题，提出了分组遗传算法.文献[3]在理想化单机MOPJ调度模型的基础上, 增加了订单准备时间因素，提出了列生成启发式算法并对其进行有效求解.文献[4]针对理想化的单机MOPJ调度模型提出了启发式算法, 可以求解超大规模订单的调度问题.在单机MOPJ调度研究领域，文献[5]和^[6]在批调度(batch scheduling)模型中考虑了多个品种.但批调度的研究重点是对批次的调度，与本文研究的调度问题有较大区别.文献[7]对多品种、考虑换模时间以及衰退效应约束的单机MOPJ调度问题进行了研究，但每个品种所使用的晶舟数量是确定的.优化晶舟在每个品种间的分配可以明显提高MOPJ调度的效率，具有实用性和研究价值，目前鲜有文献对其进行研究.

参数调整是为保证某产品的加工质量，若设备连续加工其他产品超过一定阈值，则加工该产品前需要调整参数.晶圆制造系统中，已不乏研究引入参数调整约束后的调度.文献[8]在多作业族的单机调度模型中考虑了参数调整约束，提出了简单启发式算法.文献[9]在多目标的并行机批调度问题中考虑了参数调整，并提出了蚁群优化算法.在MOPJ调度问题中考虑参数调整以保证加工过程中的质量，具有实用性和普遍性，而目前鲜有文献探讨参数调整背景下的MOPJ调度问题.

本文研究的单机MOPJ调度问题以总加权完成时间最小为目标函数，同时考虑换模时间、参数调整、订单品种多样性等约束，优化订单的分配，晶舟的加工顺序以及晶舟在品种间的分配.

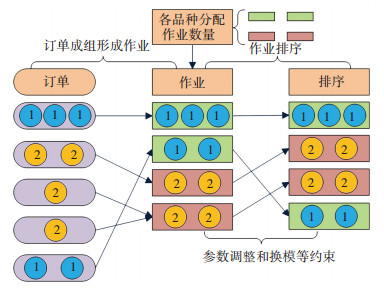
以往研究单机MOPJ调度问题，主要包含订单成组形成作业和作业排序两个子问题.如图 1所示，本文所研究的问题还需确定如何在每个品种间分配晶舟(为与调度术语一致，本文将用作业指代晶舟)，同时在作业排序时，考虑了参数调整.

Figure 1

图 1 单机MOPJ调度问题实例 Figure 1 The instance of a single machine MOPJ scheduling problem

为有效地描述调度问题，在文献[7]的基础上，做如下假设：1) 订单需保持完整性；2) 每个订单只含有一种产品，不同订单的产品种类可以不同；3) 每个作业只含有同个品种的多个订单；4) 每一个作业中载有的晶圆数不能超过其承载上限；5) 作业的数量能够满足调度要求；6) 不同品种的订单形成的作业，属于不同的作业族，即一个品种对应一个作业族；7) 设备连续加工不同作业族的两个作业时考虑换模时间；8) 设备若超过一定次数未加工过某作业族，当加工该作业族的作业时需考虑参数调整时间；9) 设备一旦开始工作，除换模外，不会中断工作；10) 同一个作业中的所有订单有相同的完工时间；11) 订单大小为0的订单，称为虚拟订单，虚拟订单在实际中不参与调度.

为方便描述，现定义符号如下：I为订单数；I_f为订单数最多的品种的订单数量；i_f为订单索引，表示品种f的第i个订单；F为总的品种数量；f为品种索引，表示第f个品种；J为总作业数；j_f为作业族f的作业数量；j为作业索引，表示第j个作业；N为总的作业数量；Q为晶舟承载的上限；C^f_if为品种f的第i_f个订单的完成时间；C_j为作业j的完成时间；p_f为品种f单位晶圆的加工时间；s_f为品种f的换模时间；q_f为品种f的参数调整时间；n_f为品种f的参数调整的阈值；σ^f_if为品种f的第i_f个订单的大小；Y^f_if为品种f的第i_f个订单，若不为虚拟订单，则其值为1，反之为0.

决策变量：X^f_ifj为若品种f的第i_f个订单被分配到j上，则其值为1，反之为0；Z_j^f为若第j个作业属于作业族f，则其值为1，反之为0；U_j为若第j个作业需要换模，则其值为1，反之为0；V_j为若第j个作业需要参数调整，则其值为1，反之为0.

由假设1) 和11) 可知，一个客户订单只能分配到一个作业中，虚拟订单不对应任何作业，即需满足

由假设2)~4) 可知，一个作业至少包含一个订单，且作业的大小不得超出上限Q，即需同时满足

由假设2)、3) 和6) 可知，一个作业只能属于一个作业族，订单的品种与作业族相对应，即满足

由假设5) 可知，所有的订单都应该被分配到作业中，当作业总数为一定值时，各个品种的作业的数量需满足调度要求，且参与调度的作业能被有效利用，即不同品种订单形成的作业的数量需满足

式中:M为一正实数，$M = \sum\limits_{{i_f} = 1}^{{I_f}} {Y_{{i_f}}^f\sigma _{{i_f}}^f/Q}, \left\lfloor M \right\rfloor $表示不大于M的最大整数.

在假设7) 和文献[8]的基础上可知，设备前后连续加工不同作业族的两个作业时需考虑换模，即需满足

在假设8) 和文献[8]的基础上可知，设备若超过一定次数未加工过某作业族，当加工该作业族的作业时, 需考虑参数调整时间，即需满足

由假设9) 可知，只有当前一个作业完成加工后，后一个作业才能进行加工，即需满足

由假设10) 可知，每一个订单的完成时间与其所分配作业的完成时间相等，即需满足

根据文献[4]，调度目标为最小化每个订单的完成时间之和，即最小化订单的总完成时间

为了进一步深入分析问题，针对构建的模型，给出了相关的引理、定理.

定理1 若有m个从小到大排序的相同品种的订单需要分配到连续两个作业j和j-1中，x表示m中的第x个订单，σ_i表示第i个订单的大小，若x及之前的订单中最大订单小于x之后所有订单大小的1/(x-1)，且x之后的订单不满足上述关系，同时$\sum\nolimits_{i = x + 1}^m {{\sigma _i} < Q, \sum\nolimits_{i = 1}^x {{\sigma _i} < Q} } $，此时将x及之前的订单分配到j-1作业，x之后的订单分配到j作业中，所获得的方案具有较优的解.

证明 假设调度S₁为将x订单及其之前的订单分配到作业j-1中，之后的订单分配到作业j中; 调度S₂为将x订单之前的订单分配到j-1中，x订单及之后的订单分配到j中; 调度S₃为将x+1订单及其之前的订单分配到j-1中，之后的订单分配到j中. 3种调度的总完成时间分别为TC(S₁)、TC(S₂)、TC(S₃), 且

则$TC({S_2})-TC({S_1}) = \sum\nolimits_{i = x + 1}^m {{\sigma _i}-} (x-1){\sigma _x}$.

从条件可知，${\sigma _x} \le \sum\nolimits_{i = x + 1}^m {{\sigma _i}/(x-1)} $，因此TC(S₂)-TC(S₁)≥0.

同理可证$TC({S_3})-TC({S_1}) = x{\sigma _{x + 1}}-\sum\nolimits_{i = x + 2}^m {{\sigma _i}} $，且其值不为负.上述定理得证.

引理1 若一个作业安排在j位置进行加工，可获得较优的解，不影响参数调整和换模的条件下，具有相同订单的作业安排的位置应与其相邻.

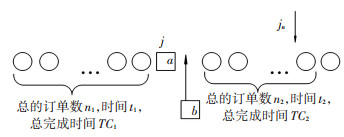
证明 如图 2所示，假设位置j之前的所有作业包含的订单数为n₁，时间为t₁，完成时间为TC₁，j_n为j位置后任意一个位置，位置j及j_n间所有作业包含的订单数为n₂，时间为t₂，总完成时间为TC₂，作业a及作业b包含的订单数量都为n，作业的处理时间为p.

Figure 2

图 2 作业位置的确定 Figure 2 Location of jobs

若作业a在j位置上获得的解较优，则满足关系

同样作业b在作业j+1位置上较其他位置亦满足关系

此时的解较优.

定理2 参考文献[4]，若作业a与作业b为相同作业族f中的作业，且满足

将作业a的位置安排在作业b的位置前，即j_a < j_b，此时获得的方案较优.

证明 令调度S₁为作业a在作业b之前，调度S₂为作业b在作业a之前.假设作业a和作业b相邻，且已经加工的时间为t, 令

则

那么, TC(S₂)-TC(S₁)=p_f(k_al_b-k_bl_a)，由条件可知, k_al_b>k_bl_a，且p_f为品种f单位晶圆的加工时间，p_f>0，因此, TC(S₂)-TC(S₁)>0.

假设作业a和作业b不相邻，上述条件相同，则将作业a及作业b分别拆分成l_a和l_b个大小为1的作业，并结合引理1，可证得，作业a位置较作业b位置靠前的方案较优.

文中将所要解决的问题分为3个层级，分别为1) 作业在品种间的分配；2) 订单成组形成作业；3) 作业的排序.虽然不少文献提供了解决包含2)、3) 子问题的MOPJ调度问题的方法，但依然缺少解决3个层级结构问题的理论方法，原有的方法也很难扩展解决类似的问题.同时由于考虑了参数调整，因此文中2)、3) 子问题涉及了订单、作业以及作业族3个层次的调度，与传统的订单、作业两个层次的调度不同.因此在上述模型和定理的基础上，提出了订单成组算法以及混合差分进化的入侵杂草算法.

订单成组算法以定理1、2为基础，可以在极短时间内解决子问题2).假设品种f的订单数量为m，大小分别为σ₁, σ₂, …, σ_m，分配的作业数量为n.定义作业容量为作业中所包含的订单的数量.

其具体步骤如下：

步骤1 将订单按照从大到小的顺序排列，即σ₁≥σ₂≥σ₃…≥σ_m.

步骤2 计算$a = \left\lfloor {m/n} \right\rfloor, b = m-an$.

式中$\left\lfloor {m/n} \right\rfloor $表示不大于m/n的最大整数.

若b≥1，则作业1至作业b的作业容量为a+1，作业b+1至作业n的作业容量为a;

若b=0，则所有作业的作业容量为a.

步骤3 从最后一个作业开始将订单按照顺序分配到作业中，每一次分配先检查当前订单是否可以分配到已分配订单的作业中，且保证作业容量不超过上述分配的容量，否则分配到最新的作业中.越靠后的作业优先分配.

步骤4 若步骤3中没有作业可以分配，且已无未分配订单的作业.根据剩余订单的数量m_r，将作业1至作业m_r的作业容量加1.

步骤5 根据定理2，将所有作业进行排序.

混合差分进化的入侵杂草算法(hybrid invasive weed optimization-differential evolution, HIWO-DE)以双层嵌套的编码机制为基础，将差分进化及订单成组算法融合到入侵杂草算法的每一次迭代中.同时在变异操作中，提出了具有学习机制(learning mechanism)的算子，学习作业在前几代中的排序，调节变异算子的大小，以使作业向理想的排序靠近.在变异操作和邻域操作算子中插入了自适应算子，使得算法在前期具有较大的搜索空间，后期具有较强的局部搜索能力.

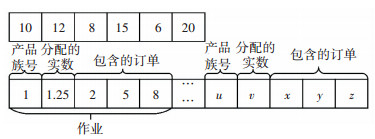
步骤1 编码.采用双层嵌套的编码方式，如图 3所示.第一层采用正整数编码，表示为杂草个体，每一个正整数表示每一个品种分配的作业数量.第二层采用的编码中，每一个作业的第一个位置为作业族编号；第二个位置为随机实数，所有作业的第二个位置的随机实数组成目标向量，随机实数从小到大排序，决定了作业的加工顺序；其他位置表示该作业所包含的订单.第二层编码中每一个作业族作业数对应第一层编码中的正整数.

Figure 3

图 3 编码方式 Figure 3 Encoding presentation

步骤2 初始化.

1) 初始化杂草个体.利用约束(6~8) 为每一品种限定作业数量的范围，采用随机生成的方法，为每一品种产生正整数，即为一个杂草个体，正整数表示作业数量. λ个杂草个体构成一个分散性较好的初始群体.

2) 初始化目标向量.为每一个作业族中的作业产生一个随机数，并从小到大排序.所有作业族中的随机数都从小到大进行排序，产生一个初始化目标向量.每一个杂草个体产生μ个目标向量，组成次群体.

步骤3 每一个杂草个体进行订单成组(2.1订单成组算法).将成组排序后的作业与步骤2.2产生的随机数对应.

步骤4 变异.以当前次种群中目标函数值最优的个体作为扰动向量，再从次种群中随机选择两个不同个体作为差分向量，通过下面公式得到变异向量:

式中：p、p₁、p₂、best∈{1, 2, …, μ}，且p₁≠p₂，best表示次群体中目标函数值最优的个体；x_{p, rf, G}、x_{p1, rf, G}、x_{p2, rf, G}、x_{best, rf, G}分别表示为第G代的p、p₁、p₂、best个体中的f品种的第r_f个作业的向量；F₁为自适应缩放算子，F₂为学习算子.

F₁较大时，变异的随机性较大，不利于找到精确的最优解；F₁较小时，收敛速度较快，且易收敛于非最优解.为避免早熟，F₁值在算法初期应较大，保持个体的多样性，易找到全局的最优解；在算法后期，F₁的值应较小，易于最优解的搜索和稳定. F₂则根据历代的状态调节数值大小，若向量有增大的趋势，则取正值；若向量有减小的趋势，则取负值.根据文献[10-13]的设计规则，得

式中：F₀为缩放因子，G_m为最大内层进化代数，G为当前内层代数，Δk_rf表示作业r_f在G代与G-1代中的位置差，ΔK^max_ff表示历代中作业r_f的最大位置差.

步骤5 交叉.交叉操作是在变异产生的第p个个体v_{p, G}和种群中的第p个体x_{p, G}之间进行，交叉得到试验向量

式中：CR为交叉因子，rand(r_f)为评价作业r_f时产生均匀分布的随机数，rnb(r_f)为随机选择的整数.

每一作业族中，将交叉后得到的数从小到大重新对应到每个作业中.

步骤6 目标向量选择.选择操作是在试验向量u_{p, G+1}与原种群的个体x_{p, G}之间进行，选择的原则是目标函数值更优的个体进入到下一代，用公式表示为

式中f为目标函数.

步骤7 种子数量确定.在文献[14-15]的基础上，采用基于个体目标函数值产生种子，种子数量计算方式为

式中：φ_min和φ_max分别为最小和最大的种子数量，f_min和f_max分别为最小和最大的目标函数值，φ_λ表示λ个体的种子数量，f_λ表示λ个体的目标函数值.

步骤8 邻域操作算子.针对每个作业族的作业，设计两种操作算子，±1变异和自适应随机变异.

±1变异，随机选择两个作业族，对其中一个作业族的作业数量+1，另一个作业族的作业数量-1.

自适应随机变异采用如下公式确定变异的最大范围值

式中：rang_max和rang_min分别为最大和最小允许变异的值，g_m为最大外层进化代数，g为当前外层代数.

在[1, c]中随机确定一个值d，选择两个作业族，其中一个作业族加上d，另一个作业族减去d.

步骤9 产生种子.随机选择一种邻域操作算子，对杂草个体执行操作，新个体即为当前个体的种子.

步骤10 竞争排除.将种群中的父代个体及子代个体按照目标函数值排序，选择较好且互不相同的λ个个体作为下一代的种群.

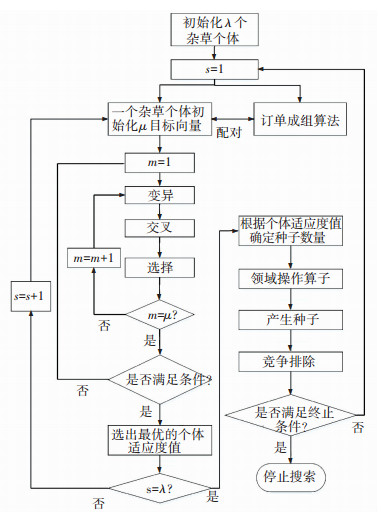
算法的总体流程图如图 4所示.

Figure 4

图 4 算法总体流程 Figure 4 Framework of the algorithm

为有效评价算法的性能，本文以求解时间和文献[16]中提出的解的优度PR作为算法评价指标, PR=V(H, T, Y)/Best(Y)，其中V(H, T, Y)表示算法H在迭代次数为T时对实例Y的求解结果，Best(Y)表示对实例Y求解所能得到的最优值.解的优度能够较好地反映算法的收敛性能，其值越小，表明算法的收敛性能越好.

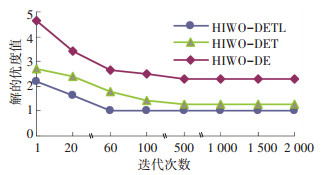
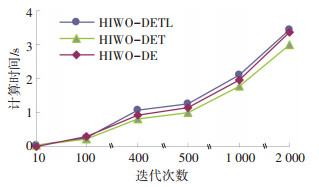
实验参数参照文献[2, 16]中的参数设计规则设定.为确定较佳的内层迭代次数，根据约束(6~8) 的作业分配约束，产生10个实例作为杂草个体进行实验，并与未使用定理2(Theorem2)、未使用学习算子的差分进化进行对比，得到迭代次数对解的优度值和求解时间的影响, 结果分别见图 5和图 6.

Figure 5

图 5 迭代次数对解的优度值的影响 Figure 5 Impact on the performance ratio by the iteration times

Figure 6

图 6 迭代次数对计算时间的影响 Figure 6 Impact on computation time by the iteration times

由图 5可知，结合了学习算子和定理2的算法在对作业进行排序时明显优于其他两种算法的收敛性，且可以看出当迭代次数为300~2 000时，3种算法的解都趋于稳定.同时可以看出结合了学习算子以及定理2后，算法的收敛速度更快，当迭代次数为60时已经找到了较稳定的解.综合考虑时间成本和解的优度，本文认为后续实验中，HIWO-DETL(HIWO-DE-Theorem2-Learning)算法的内层迭代次数定为100，HIWO-DET(HIWO-DE-Theorem2) 算法的内层迭代次数定为250，HIWO-DE算法的内层迭代次数定为300是合理的.

用类似的方法，按照不同的参数组合，进行大量实验.通过分析实验结果得到:将算法的外层初始种群λ设为10，内层初始种群μ设为20，缩放因子F₀设为0.6，交叉因子CR设为0.5，最大与最小允许变异的值rang_max、rang_min分别设为5和1，最大与最小种子数量φ_max、φ_min设为6和1，外层迭代次数g_m定为10，可以以较高的效率对问题进行求解.

利用2.1所提出的订单成组算法(记H1) 对单品种背景下的单机MOPJ调度问题进行订单成组和作业排序，对比文献[4]所提出的启发式算法(记H2)，为说明H1优于H2，以解的比值及时间作为评价指标，如表 1所示.

表 1

表 1 H1与H2的对比 Table 1 Comparison between H1 and H2 N H1 H2 比值 时间/ms 比值 时间/ms 100 0.83 10 1 16 500 0.79 12 1 25 1 000 0.78 16 1 31 5 000 0.77 281 1 374 10 000 0.78 983 1 1 139

表 1 H1与H2的对比 Table 1 Comparison between H1 and H2

从表 1可知, H1算法所求的解显著优于H2所求的解，且时间较H2更短.可见本文提出的方法在解决单品种问题上具有明显的优势.由于本算法的优势，也使得本文在解决多品种问题及品种间的晶舟分配问题具有良好的性能.

对比4种算法在不同的作业数量及订单数量的情况下解的优度值，实验结果如表 2所示.

表 2

表 2 相关解的优度值 Table 2 Performance ratio of the related solutions I J m f HIWO-DETL HIWO-DET HIWO-DE DE 50 30 [3, 18] 7 1.013 3 1.363 6 1.589 0 1.613 6 20 [3, 8] 7 1.067 5 1.110 4 1.274 4 1.755 8 50 35 [3, 18] 7 1.011 2 1.154 6 1.387 2 1.474 6 25 [3, 8] 7 1.077 4 1.084 5 1.121 3 1.666 9 50 40 [3, 18] 7 1.002 0 1.207 2 1.298 8 1.367 9 30 [3, 8] 7 1.002 2 1.107 5 1.159 9 1.479 9 100 60 [3, 18] 7 1.017 9 1.229 9 1.378 3 1.368 5 30 [3, 8] 7 1.060 6 1.391 1 1.636 6 3.459 1 100 70 [3, 18] 7 1.008 8 1.054 2 1.141 0 1.228 5 35 [3, 8] 7 1.064 7 1.292 6 1.382 0 1.334 0 100 80 [3, 18] 7 1.024 6 1.033 8 1.173 7 1.152 8 40 [3, 8] 7 1.092 7 1.356 6 1.469 8 1.561 3

表 2 相关解的优度值 Table 2 Performance ratio of the related solutions

从表 2可以看出，HIWO-DETL算法的优度值明显优于其他3种算法.由于DE算法在对问题进行求解时，无法合理分配各个品种的作业数量，因此在求解开始随机给定了每个品种的作业数量，只能求解在该作业分配的情况下较优的调度方案，而无法解决作业在各个品种间的分配问题.因此其他几个算法所求得的解要优于DE算法.故本文所提的算法可以在解决单机MOPJ问题的同时，有效解决晶舟在品种间的分配，优化调度方案.

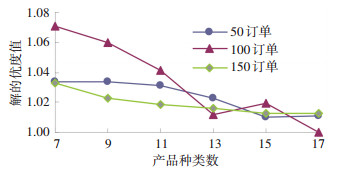
对产品种类数为7、9、11、13、15、17, 对应的订单数为50、100、150的调度问题进行仿真实验，实验结果见图 7.

Figure 7

图 7 产品种类数对解优度值的影响 Figure 7 Impact on the performance ratio by the number of product types

OS表示优化空间(optimization space)，且

式中：V(IWO-DE)表示优化了作业分配的求解结果，V(DE)表示未优化作业分配的求解结果.

由图 7易知，当订单数相同时，随着产品种类数的增加，解的优度值有下降的趋势，这与当种类数增加时，订单及作业分配的限制增加，调度组合减少，算法更容易求得较优调度结果相符.从对不同种类与订单下OS值测算的实验中发现，优化作业在品种间分配的调度较未优化的调度的性能至少提高了10%，从而说明优化作业分配在MOPJ调度中的重要性.

1) 采用双层嵌套的编码机制，以晶舟的数量为纽带将上、下层间的编码映射统一，为解决在传统单机MOPJ问题上增加晶舟分配问题的调度提供了研究思路.

2) 将差分进化融合到自适应入侵杂草算法的迭代中，同时构造具有学习机制的算子，根据历代位置，调整参数大小，改善了算法的性能，丰富了解决此类调度问题的理论方法.

3) 仿真实验表明，HIWO-DETL具有较好的求解性能，在MOPJ调度问题中考虑晶舟的优化具有一定的意义.