由于增压锅炉装置相对于常压锅炉有着体积小、效率高等优势,在能源动力领域的运用越来越广泛[1].与常压锅炉相比,增压锅炉装置各组成设备间具有更强的耦合性,为保证增压锅炉装置运行的安全性、稳定性和经济性,对增压锅炉装置动态匹配关系的研究很有必要,特别是在锅炉降负荷过程中的匹配关系[2].增压锅炉装置在降负荷过程中,由于机组转子的机械惯性,难以精确把握该在何时对相应的控制部位进行调节,以及怎么调节(以多大的速度、多大的幅度).一般做法是以保证锅炉降负荷过程中的安全、稳定为原则,在厂家给出的安全范围内进行操作,通常厂家在设定安全范围时会留有较大的裕度,因此在实际操作中往往无法发挥其最大的降负荷能力,面对紧急时刻(例如紧急刹车、紧急倒车)难免会因为来不及反应而造成损失.
近年来,一些专家学者在增压锅炉装置建模及其匹配运行等领域做了相关研究并取得相关成果[3-14].朱泳等[15]建立锅炉燃烧及蒸发系统的动态数学模型并进行仿真实验,得到了增压锅炉汽包压力、水位及过热蒸汽温度在不同负荷突降扰动下的动态响应特性;赵冬来[16]基于涡轮增压机组模型以及改进的压气机特性计算方法,建立了精度较高的涡轮增压机组稳态和动态仿真模型,对增压锅炉从低工况30%到高工况100%的加速过程进行了仿真分析;房桐毅[17]基于流体网络对涡轮增压机组在增减速过程中的流量特性,分析了不同大气温度下的功率平衡点以及过量空气系数变化对涡轮增压机组的影响.这些研究主要集中在增压锅炉及涡轮增压机组的特性分析,没有更进一步对增压锅炉的控制策略进行系统分析和研究.
本文以某型船用增压锅炉装置为对象,在分析其降负荷特性的基础上,对其进行建模,并在仿真平台上进行仿真实验,对降负荷过程的炉膛空气过余系数进行研究,通过调节锅炉降负荷速度或幅度,使空气过余系数保持在炉膛稳定燃烧允许的范围内波动,进而得到不同初始状态下的最小降负荷时间,实验结果可以指导实际监控系统的参数设定,为该型增压锅炉装置的安全运行提供支持.
1 增压锅炉装置降负荷特性分析增压锅炉装置由增压锅炉本体和涡轮增压机组组成,由于锅炉排放的烟气仍具有较高的能量,经净化处理后可以进入烟气涡轮,带动压气机为锅炉提供具有一定压力和温度的助燃空气.锅炉的热负荷主要由喷油量来决定,当锅炉降负荷(即喷油量减少时),由于涡轮增压机组转子具有一定的机械惯性,响应锅炉的降负荷需要一定时间,如果喷油量的减少速度大大超过了机组响应速度(特别是在紧急刹车、紧急倒车等喷油量减少速度比较快的情况),很容易出现炉膛内空气过余系数骤升导致熄火的情况.
空气过余系数是锅炉燃烧状态的一个重要影响因素,如果空气过余系数太小,燃料不能完全燃烧,出现冒黑烟的现象;空气过余系数也不宜过大,较大的空气过余系数会增加空气带走的热量,使得锅炉的排烟损失增加,降低锅炉热效率,当空气过余系数足够大(即进入炉膛的空气量过大)可能会造成锅炉熄火.一般船用增压锅炉的最佳空气过余系数为1.10~1.20,既可保证燃料的完全燃烧,又可以使得锅炉的排烟损失在可接受的范围内.
2 增压锅炉装置机理模型本文研究对象为某型船用增压锅炉装置.根据该型增压锅炉装置的设备组成以及工质流向,采用模块化建模方法将其划分为锅炉炉膛、涡轮增压机组、风道系统、空气夹层和烟道系统共5个模块.
2.1 锅炉炉膛炉膛是燃料和空气混合燃烧的场所,由于增压锅炉结构较为紧凑,燃烧时炉膛可作为集总参数处理,其能量守恒方程为
| $ \begin{array}{l} 0.5{m_{\rm{y}}}{c_{p{\rm{y}}}}{\rm{d}}{{\bar T}_{\rm{y}}}/{\rm{d}}t = {W_{\rm{r}}}{H_{\rm{r}}}\left( {1 - {k_{\rm{b}}}} \right) - \left( {{W_{\rm{r}}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{W_{\rm{k}}}} \right)\left( {{{\bar T}_{\rm{y}}} - {T_0}} \right) - {Q_{\rm{F}}}. \end{array} $ |
式中:my为炉膛内烟气的质量,cpy为烟气的定压比热容,Ty为烟气平均温度,Wr和Wk为喷油量和炉膛送风量,Hr为燃料的化学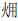
炉膛内烟气质量的计算公式为
| $ {m_{\rm{y}}} = {p_{\rm{b}}}{V_{\rm{b}}}/{R_{\rm{g}}}\bar T. $ |
式中:pb为炉膛压力,由烟道系统的流体网络模型得到,Vb为炉膛容积,Rg为理想气体状态参数.
辐射换热量QF的计算公式为
| $ {Q_{\rm{F}}} = \sigma {A_{{\rm{sl}}}}\left( {\bar T_{\rm{y}}^4 - {\varepsilon _{{\rm{sl}}}}T_{{\rm{sl}}}^4} \right). $ |
式中:σ为波尔兹曼常数,Asl和Tsl为水冷壁有效辐射面积和壁面平均温度,εsl=0.9为水冷壁灰度.
炉膛空气过余系数α的计算公式为
| $ \alpha = {W_{\rm{k}}}/\left( {13.865{W_{\rm{r}}}} \right). $ |
涡轮增压机组可以根据其设备组成再次进行模块化分解,划分为压气机、烟气涡轮、辅助汽轮机、机组转子4个模块.
2.2.1 压气机压气机主要利用烟气涡轮和辅助汽轮机提供能量,将空气压缩到一定压力和温度送入炉膛助燃.空气可视为理想气体,根据理想气体状态方程,可得压气机功率为
| $ {N_{\rm{c}}} = {G_{\rm{k}}}{c_{p{\rm{k}}}}{T_{{\rm{k0}}}}\left[ {\pi _{\rm{c}}^{\left( {{K_{\rm{k}}} - 1} \right)/{K_{\rm{k}}}} - 1} \right]/{\eta _{\rm{c}}}. $ |
式中:Gk为压气机的空气质量流量,cpk和Tk0为空气的定压比热容和进口温度,πc为压气机压比,Kk为空气绝热系数,ηc为压气机内效率.
压气机压比πc的计算公式为
| $ {\pi _{\rm{c}}} = {p_{{\rm{c}}2}}/{p_{{\rm{c}}1}}. $ |
式中pc1和pc2为压气机的进、出口压力,由风道系统的流体网络模型计算得到.
压气机流量Gk与压气机进口压力pc1、进口温度Tc1和压比πc有关,且
| $ {G_{\rm{k}}} = {f_{{\rm{cg}}}}\left( {{p_{{\rm{cl}}}},{T_{{\rm{cl}}}},{\pi _{\rm{c}}}} \right). $ |
压气机在工作过程中的能量损失包括:叶轮摩擦损失ηf、扇形损失ηθ、级间漏气损失ηy和鼓风损失ηw等,各项损失的计算公式为:
| $ \begin{array}{l} {\eta _f} = {K_{\rm{f}}}D_{\rm{c}}^5n_{\rm{c}}^3{\rho _{{\rm{k0}}}},\\ {\eta _\theta } = 0.7{\left( {{L_{\rm{c}}}/{D_{\rm{c}}}} \right)^2},\\ {\eta _{\rm{y}}} = 3.1{b_{\rm{c}}}/{h_{\rm{c}}},\\ {\eta _{\rm{w}}} = {K_{\rm{w}}}\left( {1 - {\zeta _{{\rm{wi}}}}} \right){D_{\rm{c}}}L_{\rm{c}}^{1.5}n_{\rm{c}}^3{\rho _{{\rm{k0}}}}. \end{array} $ |
式中:ρk0为压气机进口空气密度,DC、LC、bC和hC为压气机平均直径、静叶栅轴向长度、叶片顶部径向间隙和叶片平均高度,Kf、Kw和ζwi为压气机摩擦损失系数、鼓风损失系数和局部进气系数,nc为压气机转速.
综合考虑这些损失后,压气机内效率ηc可表示为
| $ {\eta _{\rm{c}}} = 1 - \left( {{\eta _f} + {\eta _\theta } + {\eta _{\rm{y}}} + {\eta _{\rm{w}}}} \right). $ |
烟气涡轮是压气机的主要功率来源,由于高温气体也可以当作理想气体处理,故烟气涡轮的输出功率为
| $ {N_{{\rm{gt}}}} = {G_{\rm{y}}}{c_{P{\rm{y}}}}{T_{{\rm{y0}}}}\left[ {1 - \varepsilon _{{\rm{gt}}}^{\left( {{k_{\rm{g}}} - 1} \right)/{k_{\rm{g}}}}} \right]{\eta _{{\rm{gt}}}}. $ |
式中:Ty0为烟气的进口温度,Gy和cPy为烟气质量流量和定压比热容,εgt为烟气膨胀比,Kg=1.35为烟气绝热系数,ηgt为烟气涡轮内效率.
烟气膨胀比εgt的计算公式为
| $ {\varepsilon _{{\rm{gt}}}} = {p_{{\rm{gt1}}}}/{p_{{\rm{gt2}}}}. $ |
式中pgt1和pgt2为烟气涡轮的进、出口压力,由烟道系统的流体网络模型计算得到.
因为烟气涡轮采用固定叶栅和冲动式叶片,故内效率可表示为膨胀比εgt的函数
| $ {\eta _{{\rm{gt}}}} = {f_{g\eta }}\left( {{\varepsilon _{{\rm{gt}}}}} \right). $ |
辅汽轮机用于当烟气涡轮功率不足或者在机组启动、加速时驱动压气机,本机组的辅汽轮机采用双列调节级,其进汽流量为
| $ {G_{{\rm{st}}}} = {G_{{\rm{st0}}}}\beta \sum\limits_{k = 0}^n {{a_k}{\theta ^k}\frac{{\left( {{p_{{\rm{gt1}}}}/{p_{{\rm{gt10}}}}} \right)}}{{\sqrt {{T_{{\rm{gt1}}}}/{T_{{\rm{gt10}}}}} }}} . $ |
式中:Gst0、pst10和Tst10为额定工况的进汽流量、压力和温度,pst1和Tst1为当前进汽压力和温度,β为流量修正系数,θ为调节阀阀位,a0~n为各阶流量拟合因子.
其中流量修正系数β的计算公式为
| $ \beta = \left\{ \begin{array}{l} 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{p_{{\rm{gt2}}}}/{p_{{\rm{gt1}}}} \le {\varepsilon _{{\rm{cr}}}};\\ \sqrt {1 - {{\left[ {\left( {\varepsilon - {\varepsilon _{{\rm{cr}}}}} \right)/\left( {1 - {\varepsilon _{{\rm{cr}}}}} \right)} \right]}^{1/2}}} ,{p_{{\rm{gt2}}}}/{p_{{\rm{gt1}}}} > {\varepsilon _{{\rm{cr}}}}. \end{array} \right. $ |
式中Pst2为汽轮机背压,εcr=0.546为过热蒸汽的临界压比.
汽轮机的输出功率在等熵膨胀时最大,且
| $ {S_{{\rm{st1}}}} = {f_S}\left( {{p_{{\rm{gt1}}}},{H_{{\rm{st1}}}}} \right);{H_{{\rm{st2}}S}} = {f_H}\left( {{p_{{\rm{gt2}}}},{S_{{\rm{st1}}}}} \right). $ |
汽轮机的实际输出功率为
| $ {N_{{\rm{st}}}} = {G_{{\rm{st}}}}{\eta _{{\rm{st}}}}\left( {{H_{{\rm{st1}}}},{H_{{\rm{st2}}S}}} \right). $ |
式中Hst2S为理想排汽焓,Sst1为进口蒸汽熵,ηst=0.87为辅助汽轮机的内效率.
2.2.4 机组转子作用在机组转子上的功率包括烟气涡轮输出功率Nst、辅助汽轮机输出功率Ngt、压气机耗功Nc和转子损失功率Nloss.
由能量守恒列出转子动力学方程为
| $ {a_{\rm{a}}} = 30\left( {{N_{{\rm{st}}}} + {N_{{\rm{gt}}}} - {N_{\rm{c}}} - {N_{{\rm{loss}}}}} \right)/\left( {{\rm{\pi }}{J_{\rm{a}}}{n_{\rm{a}}}} \right). $ |
转子损失功率的计算公式为
| $ {N_{{\rm{loss}}}} = 0.01\left( {{N_{{\rm{st}}}} + {N_{{\rm{gt}}}}} \right) + 500. $ |
根据牛顿第二定律有
| $ {a_{{\rm{gt}}}} = {a_{\rm{c}}} = {a_{\rm{a}}},{a_{{\rm{st}}}} = {K_{{\rm{gear}}}}{a_{\rm{a}}}, $ |
根据涡轮增压机组的结构(压气机和烟气涡轮共轴,而辅助汽轮机通过减速器带动压气机)有
| $ {n_{{\rm{gt}}}} = {n_{\rm{c}}} = {n_{\rm{a}}},{n_{{\rm{st}}}} = {n_{\rm{a}}}/{K_{{\rm{gear}}}}. $ |
式中:ngt、nst和nc为烟气涡轮、辅助汽轮机和压气机的转速,agt、ast和ac为烟气涡轮、辅助汽轮机和压气机的角加速度,Kgear为减速器的减速比.
2.3 空气夹层进出空气夹层的流量主要有空气夹层进风量Gjca1、炉膛进风量Gbk和空气泄漏量Gjcl,由质量守恒方程可得
| $ {K_{{\rm{NPk}}}}{V_{{\rm{jc}}}}{\rm{d}}{p_{{\rm{jc}}}}/{\rm{d}}t = {G_{{\rm{jcal}}}} - {G_{{\rm{bk}}}} - {G_{{\rm{jcl}}}}, $ |
式中pjc为空气夹层风压,KNPk为空气压缩系数,Vjc为空气夹层容积.
空气压缩系数KNPk的计算公式为
| $ {K_{{\rm{NPk}}}} = \partial {\rho _k}/\partial {p_k}. $ |
空气夹层进风量和炉膛进风量可由空气在湍流状态下的一维流动方程计算得到:
| $ \begin{array}{l} {G_{{\rm{jcal}}}} = {\xi _{{\rm{c2jc}}}}\sqrt {{p_{{\rm{c2}}}} - {p_{{\rm{jc}}}}} ,\\ {G_{{\rm{bk}}}} = {\xi _{{\rm{jc2b}}}}\sqrt {{p_{{\rm{jc}}}} - {p_{\rm{b}}}} . \end{array} $ |
式中ξc2jc和ξjc2b分别为空气夹层进风道和锅炉配风器的阻力系数.
2.4 风道系统风道系统由大气、压气机入口、压气机出口3个压力节点和大气到压气机入口、压气机出口到空气夹层两条流量支路组成.其中,大气节点的参数为给定值,压气机入口和压气机出口需要通过流体网络模型迭代计算得到.
| $ \begin{array}{l} {p_{{\rm{cl}}}} = {p_0} - {\left( {{G_{\rm{k}}}/{\xi _{{\rm{a2c}}}}} \right)^2}\\ {K_{{\rm{NPa}}}}{V_{{\rm{cpn}}}}{\rm{d}}{p_{{\rm{c2}}}}/{\rm{d}}t = {G_{\rm{k}}} - {\xi _{{\rm{c2jc}}}}\sqrt {{p_{{\rm{c2}}}} - {p_{{\rm{jc}}}}} . \end{array} $ |
式中:ξa2c和ξc2jc为大气到压气机入口和压气机出口到空气夹层的风道阻力系数,Vcpn为压气机出口风道的容积,KNPa为空气压缩系数.
2.5 烟道系统烟道系统由对流蒸发管束出口、过热器出口、经济器出口、烟气涡轮入口、烟气涡轮出口、大气6个压力节点和炉膛出口到对流蒸发管束出口、对流蒸发管束出口到过热器出口、过热器出口到经济器出口、经济器出口到烟气净化装置出口、烟气净化装置出口到烟气涡轮入口、烟气涡轮出口到烟囱出口6条流量支路组成.与风道系统类似,除大气节点外,其他几个节点压力随相应各支路的流量变化而变化,需通过流体网络模型迭代计算得到.
| $ \begin{array}{l} {p_{{\rm{gt2}}}} = {p_0} + {\left( {{G_{\rm{y}}}/{\xi _{{\rm{g2a}}}}} \right)^2},\\ {p_{{\rm{gt1}}}} = {p_{jj}} - {\left( {{G_{{\rm{geg}}}}/{\xi _{{\rm{ge}}}}} \right)^2},\\ {p_{jj}} = {p_{{\rm{gr}}}} - {\left( {{G_{{\rm{jjg}}}}/{\xi _{{\rm{jj}}}}} \right)^2},\\ {p_{{\rm{gr}}}} = {p_{{\rm{dl}}}} - {\left( {{G_{{\rm{grg}}}}/{\xi _{{\rm{gr}}}}} \right)^2},\\ {p_{{\rm{dl}}}} = {p_{\rm{b}}} - {\left( {{G_{{\rm{dlg}}}}/{x_{{\rm{dl}}}}} \right)^2}, \end{array} $ |
| $ \begin{array}{l} {K_{{\rm{NPy}}}}{V_{{\rm{ge}}}}{\rm{d}}{p_{{\rm{gt1}}}}/{\rm{d}}t = {G_{{\rm{geg}}}} - {\xi _{{\rm{g2a}}}}\sqrt {{p_{{\rm{gt2}}}} - {p_0}} ,\\ {K_{{\rm{NPy}}}}{V_{{\rm{jj}}}}{\rm{d}}{p_{{\rm{jj}}}}/{\rm{d}}t = {G_{{\rm{jjg}}}} - {G_{{\rm{geg}}}},\\ {K_{{\rm{NPy}}}}{V_{{\rm{gr}}}}{\rm{d}}{p_{{\rm{gr}}}}/{\rm{d}}t = {G_{{\rm{grg}}}} - {G_{{\rm{jjg}}}},\\ {K_{{\rm{NPy}}}}{V_{{\rm{dl}}}}{\rm{d}}{p_{{\rm{dl}}}}/{\rm{d}}t = {G_{{\rm{dlg}}}} - {G_{{\rm{grg}}}},\\ {K_{{\rm{NPy}}}}{V_{\rm{b}}}{\rm{d}}{p_{\rm{b}}}/{\rm{d}}t = {G_{{\rm{jca2}}}} + {G_{{\rm{boil}}}} - {G_{{\rm{dlg}}}}. \end{array} $ |
式中:ξg2a、ξge、ξjj、ξgr和ξdl为烟囱、烟气净化装置、经济器、过热器和对流蒸发管束的阻力系数,pgt2、pgt1、pjj、pgr和pdl为烟气涡轮出口、烟气涡轮入口、经济器出口、过热器出口和对流蒸发管束出口的烟气压力,Ggeg、Gjjg、Ggrg、Gdlg、Gjca2和Gboil为烟气净化装置烟气流量、经济器烟气流量、过热器烟气流量、对流蒸发管束烟气流量、炉膛进风量和炉膛喷油量,Vge、Vjj、Vgr、Vdl和Vb为烟气净化装置、经济器、过热器、对流蒸发管束和炉膛内烟气流通部分的容积,KNPy为烟气压缩系数.
利用上述模型和已有研究成果[3-4, 7-8],在SimuWorks仿真支撑平台上搭建某型船用增压锅炉装置的全系统模型,其拓扑结构如图 1所示.

|
图 1 某型增压锅炉装置模型的拓扑结构图 Figure 1 Topological structure diagram of supercharged boiler model |
由于空气过余系数过大或者过小都会造成锅炉熄火,为了直观地从实验结果得到分析结论,在仿真实验中设置了空气过余系数边界值.上、下边界值分别反映了在保证锅炉燃烧稳定(不熄火)的条件下,能够允许的最大和最小进风量.由于空气过余系数边界值与锅炉结构有关,本实验根据实际锅炉的运行数据,将空气过余系数上边界取为2.3,空气过余系数下边界取为0.8,也即当空气过余系数在0.8~2.3时,认为锅炉燃烧稳定.
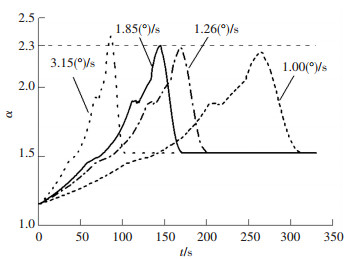
3.1 匀速降负荷仿真实验与结果分析假设当前锅炉处于全负荷稳定运行状态(燃油流量调节阀角度315 °).记初始状态的时刻为t=0 s,在t=2 s时,以不同速度均匀关小燃油流量调节阀减少喷油量,使锅炉从全负荷逐步降低至最小负荷(燃油流量调节阀角度0°),实验结果如图 2所示,各曲线表示不同关阀速度下空气过余系数的变化曲线(关阀速度从左往右分别为3.15、1.85、1.26、1.00(°)/s).
|
图 2 不同关阀速度下空气过余系数的变化曲线 Figure 2 Changing curve of excess air coefficient when valve closed with different speeds |
由图 2可见,由于喷油量下降,烟气流量和参数降低,但是涡轮增压机组的机械惯性使机组转速不会立即响应烟气流量和参数的变化,锅炉的进风量不会马上下降,空气过余系数将上升,而且上升速度与燃油流量调节阀的关阀速度成正比,达到最高点的时间与关阀速度成反比.当燃油流量调节阀的关阀速度为1.85(°)/s时,空气过余系数最大值为2.3,过渡过程时间为172 s.由此可见,该型增压锅炉在匀速降负荷时,燃油流量调节阀的关闭速度不能超过1.85 (°)/s.所得关阀速度略大于船上的实际操作速度,考虑到实际操作留有的安全裕度,这个极限速度是合理的,由此可以看出仿真结果的逼真度,同时通过对仿真模型与实船试验在不同工况基本参数的对比,误差控制在0.3%以内,进一步说明仿真模型的正确性,即可以认为仿真模型达到了仿真试验的要求.
3.2 快速降负荷真实验与结果分析如何使锅炉在保证安全运行的前提下,在最短时间内降至目标负荷非常重要.本节在匀速降负荷仿真实验的基础上,进一步研究增压锅炉的快速降负荷控制策略.
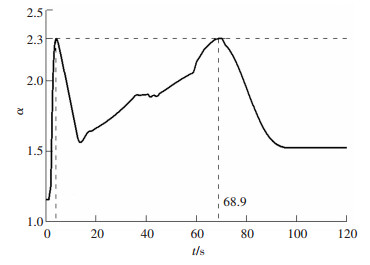
初始状态仍取全负荷稳定运行状态,但采取两段式降负荷控制策略,在t=2 s时第1次降负荷,待空气过余系数下降到1.6左右时再进行第2次降负荷.第1次降负荷采用突降方式,而第2次降负荷采用匀速降负荷方式.通过多次仿真实验得到一种可行的快速降负荷策略,如图 3所示.
|
图 3 两段式降负荷时空气过余系数的变化曲线 Figure 3 Changing curve of excess air coefficient during the process of two-stage load down |
由图 3可见,第1次降负荷可以不考虑人的操作速度和调节阀的开关速度,直接突降至全负荷的47.27%,此时空气过余系数可以控制在稳定燃烧的范围内,并在t=4.1 s时达到最大边界值2.3;在t=13.7 s,空气过余系数下降至1.61,此时以1.85(°)/s的关阀速度进行第2次降负荷,锅炉依然能够正常燃烧,并在t=96.7 s时重新稳定.
对比图 2、3可见,两段式降负荷的过渡过程时间(96.7 s)只是全程匀速降负荷(172 s)的56.22%,这主要是因为第一段突降负荷过程节省了大量时间.
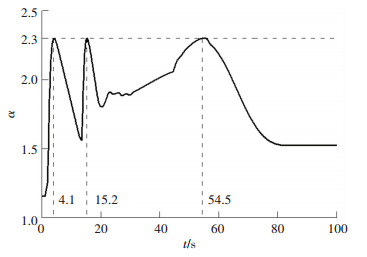
那么是否分段越多,降负荷时间越短?通过三段降负荷实验进行验证,前两段采用突降方式,分别在t=2 s和13.7 s时突降至全负荷的47.27%和30%;第三段采用1.85(°)/s匀速降负荷,结果如图 4所示.
|
图 4 3段式降负荷时空气过余系数的变化曲线 Figure 4 Changing curve of excess air coefficient during the process of three-stage load down |
对比图 2~4可见,3段式降负荷的过渡过程时间更短,在t=82.3 s时锅炉即可重新稳定.
通过快速降负荷仿真实验可见,分段降负荷的控制策略优于全程匀速降负荷.但是在本文研究中,每次降负荷都是在空气过余系数稳定后再进行的,因此得到的结论可能不是最优结果,下一步工作可以更进一步地研究各分段之间的最优匹配关系,确定各分段的开始与结束时间,在保证锅炉燃烧稳定的前提下,使降负荷的过渡过程时间最短.
4 结论本文对增压锅炉装置降负荷特性进行了分析,并采用模块化建模方法对某型船用增压锅炉装置进行了机理建模,最后通过仿真实验对该型增压锅炉的降负荷控制策略进行研究:
1) 该型增压锅炉全程匀速降负荷时的燃油流量调节阀最大关阀速度为1.85(°)/s,过渡过程时间为172 s.
2) 分段降负荷策略优于全程匀速降负荷,从降负荷到稳定的时间短,而且分段数越多,时间越短.
以上结论可以为实际监控系统设计和调节阀的参数设定提供参考,同时也可以为调节、控制与保护逻辑和算法研究提供支持.
| [1] | 李章, 张宁, 刘翔源, 等. 船用增压锅炉装置[M]. 北京: 海潮出版社, 2009. |
| [2] | HARYANTO A, HONG K S. Modelling and simulation of an oxy-fuel combustion boiler system with flue gas recirculation[J]. Computers and Chemical Engineering, 2011, 35(1): 25-40. DOI: 10.1016/j.compchemeng.2010.05.001 |
| [3] |
陈坚红, 乔庆, 张宝, 等. 汽轮机调节级临界压比特性[J].
浙江大学学报(工学版), 2014, 48(11): 2072-2079.
CHEN Jianhong, QIAO Qing, ZHANG Bao, et al. Critical pressure ratio characteristics of steam turbine governing stage[J]. Journal of Zhejiang University(Engineering Science), 2014, 48(11): 2072-2079. |
| [4] |
胡继敏, 金家善. 船用增压锅炉系统动态数学模型的建立[J].
计算机与数字工程, 2012, 34(1): 50-54.
HU Jimin, JIN Jiashan. Dynamic mahematical model of marine supercharged boiler system[J]. Computer and Digital Engineering, 2012, 34(1): 50-54. |
| [5] | ZHANG Hongyan, XIE Haitao, JIN Xiangdong. The simulation of heat transfer and flow performance for supercharged boiler superhea-ter[J]. Advanced Materials Research, 2014, 936: 2103-2108. DOI: 10.4028/www.scientific.net/AMR.936.2103 |
| [6] | HIDEAKI T, TOMOKI K. A novel experimental method to evaluate the impact of volute's asymmetry on the performance of a high pressure ratio turbocharge compressor[J]. Science China Technological Sciences, 2012, 55(6): 1695-1700. DOI: 10.1007/s11431-012-4822-9 |
| [7] | WANG Peng, ZHU Qidan, XIE Haitao, et al. The study of level control strategy for supercharged boiler drum based on fuzzy control[J]. Applied Mechanics & Materials, 2014, 687-691: 216-219. DOI: 10.4028/www.scientific.net/AMM.687-691.216 |
| [8] | ZHANG Yangjun, CHEN Tao, ZHUGE Weilin, et al. An integrated turbocharger design approach to improve engine performance[J]. Science China Technological Sciences, 2010, 53(1): 69-74. DOI: 10.1007/s11431-009-0421-9 |
| [9] |
倪何, 肖航, 曾凡明, 等. 基于残差修正的涡轮增压机组差异演化建模与降负荷特性分析[J].
上海交通大学学报, 2015, 49(5): 620-625.
NI He, XIAO Hang, ZENG Fanming, et al. Differential evolutionary modeling with residual correction and down-load characteristic analysis for marine turbocharged unit[J]. Journal of Shanghai Jiaotong University, 2015, 49(5): 620-625. DOI: 10.16183/j.cnki.jsjtu.2015.05.008 |
| [10] | ZHANG Hongyan, JIN Xiangdong, XIE Haitao. The study of water level fuzzy control for supercharged boiler drum[J]. Advanced Materials Research, 2014, 936: 2165-2170. DOI: 10.4028/www.scientific.net/AMR.936.2165 |
| [11] | ZHAO Jiafeng, MA Xiuzhen, ZHAO Shizhou, et al. Hammerstein identification of supercharged boiler superheated steam pressure using Laguerre-Fuzzy model[J]. International Journal of Heat & Mass Transfer, 2014, 70(2): 33-39. DOI: 10.1016/j.ijheatmasstransfer.2013.10.056 |
| [12] | ZHENG Xinwei, HU Xuecong, WANG Zhiyu, et al. Research on the connection type between evaporating tube bundle and a steam drum shell on a natural circulation marine supercharged boiler[J]. Applied Mechanics & Materials, 2014, 618: 448-452. DOI: 10.4028/www.Scientific.net/AMM.618.448 |
| [13] | SONG Fei, CHENG Gang, SUN Fengrui, et al. Reconstruction of key parameters of marine supercharged boiler based on PLS-SVM[J]. Advanced Materials Research, 2013, 859: 19-22. DOI: 10.4028/www.scientific.net/AMR.859.19 |
| [14] | HU Jimin, JIN Jiashan, YAN Zhiteng. Fluid-solid coupling numerical simulation of charge process in variable-mass thermodynamic system[J]. Journal of Central South University, 2012, 19(4): 1063-1072. DOI: 10.1007/s11771-012-1110-6 |
| [15] |
朱泳, 金家善, 严志腾, 等. 船用增压锅炉响应负荷突降的特性仿真分析[J].
中南大学学报(自然科学版), 2013, 44(9): 3678-3686.
ZHU Yong, JIN Jiashan, YAN Zhiteng, et al. Simulation analysis of responding characteristics on abrupt load dropping for marine supercharged boilers[J]. Journal of Central South University (Science and Technology), 2013, 44(9): 3678-3686. |
| [16] |
赵冬来. 基于Simulink的涡轮增压机组匹配特性仿真研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
ZHAO Donglai. The simulation of matching characteristics of turbocharger unit based on simulink[D]. Harbin: Harbin Engineering University, 2012. |
| [17] |
房桐毅. 基于流体网络的涡轮增压机组匹配特性仿真研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
FANG Tongyi. Simulation research on match characteristics of turbocharger unit by flow net[D]. Harbin: Harbin Engineering University, 2012. |
 2017, Vol. 49
2017, Vol. 49


