微气泡减阻具有较好的减阻效果和较弱的环境响应[1],其被认为是最有效的减阻方式之一. McCormick等[2]利用电解产生氢气泡的方法实现了减阻;Madvan等[3]采用多普勒测速仪研究了微气泡对湍流边界层的表面摩擦阻力的影响;Jinho等[4]采用平板表面注气的方法实现减阻;Yoshiaki等[5]在循环水槽中针对不同平板进行了微气泡减阻实验;Kato等[6-7]进行了平板微气泡减阻实验,研究了气孔直径对减阻效果的影响特性,结果表明气孔直径对减阻效果影响极大;Sheng等[8]通过田口分析法研究了通气量、通气面积、气泡尺寸及来流速度对平板微气泡减阻效果的影响,结果表明通气量是主要影响因素;Deutsch等[9-10]采用通气缝出流方式,针对回转体模型研究了轴向压力梯度及气体成分对减阻效果的影响;Sanders等[11]提出了通过多孔质板向平板边界层内注入微气泡的方式,研究了不同速度下减阻效果随通气量的变化特性;Elbing等[12]改进了通气缝式出流方式,并对比了不同出流方式下的减阻效果.董文才等[13]通过在回转体模型首部及中部开孔的方式,研究了不同区域组合通气对气泡减阻效果的影响;傅慧萍[14]研究了重力对平板气泡减阻的影响特性,认为重力对气泡减阻效率影响较大;李杰等[15]探索了尺寸效应及雷诺数对气泡减阻的影响特性.由于通气两相流非定常过程的影响,模型阻力曲线会出现脉动现象,继而影响水中航行体的稳定性.而目前针对气泡减阻的研究都是以阻力为研究对象进行的,并未对阻力时域曲线进行脉动分析.
本文针对微孔阵列式绕回转体模型,在封闭循环水洞中进行了通气两相流非定常特性实验研究,讨论了雷诺数Re及通气率Qv对流动非定常特性及模型水阻力脉动特性的影响.
1 实验设备实验在循环水洞中进行,水洞具体参数参见文献[16].研究中采用六分力天平、水下绝压传感器、数据采集系统和高速摄像观察系统,分别对实验过程中的模型水阻力、通气量、流速、流场等进行记录.
实验模型如图 1所示,六分力天平安装于实验模型尾部,并与水洞尾支撑段固定连接.天平测得的模型阻力数据通过动态测试分析系统进行采集,采集频率为1 024 Hz,采集时间为8 s,测量误差±0.1 N.模型尾部距轴线16 mm处安装水下绝压传感器,压力传感器量程为0~100 kPa,线性精度为0.2%FS,采集频率为1 024 Hz,采集时间为8 s.回转体模型长250 mm、直径40 mm,采用流线型头型以降低流场扰流对气泡减阻实验的影响.模型表面微孔孔径为0.8 mm,沿轴向等距交错分布,共4排,排间距12 mm,首排孔距头部40 mm;每排共8个,且沿圆周方向均匀布置.

|
图 1 实验模型 Figure 1 The experimental model |
本研究定义雷诺数Re、通气率Qv、压力系数Cp、阻力系数CD作为量纲一参数,且
| $ \begin{array}{l} Re = VL/\upsilon, {\rm{ }}{Q_v} = {Q_{in}}/\left( {VS} \right), \\ {C_p} = p/(0.5\rho {V^2}), {\rm{ }}{C_{\rm{D}}} = R/(0.5\rho {V^2}S). \end{array} $ |
式中:V为水洞工作段流速,L为实验模型长度,υ为水的动力黏度,Qin为通气量,S为回转体截面积,p为模型尾部压力,R为模型阻力.
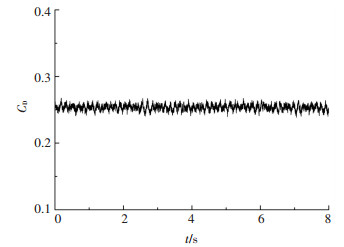
2.1 典型工况下的非定常特性分析本节通过分析模型水动力时域、频域曲线及流场形态,研究典型工况下的绕流线型回转体通气两相流动的非定常特性. 图 2为雷诺数Re=2.03×106、通气率Qv=0.014下模型阻力系数的时域曲线.由图 2可知,测量时间内阻力系数平均值基本不变,且阻力系数存在周期性脉动现象.
|
图 2 阻力系数时域曲线(Re=2.03×106,Qv =0.014) Figure 2 Drag coefficient versus time(Re=2.03×106, Qv=0.014) |
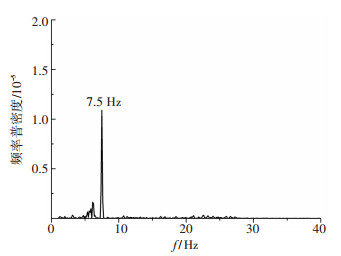
为了更好地研究典型工况下的实验模型阻力系数的脉动特性,分析脉动频率,采用FFT变换将实验模型阻力系数信号的时域特性转换为频域特性进行分析. 图 3为雷诺数Re=2.03×106、通气率Qv=0.014下模型阻力系数的频域曲线.
|
图 3 阻力系数频域曲线(Re=2.03×106,Qv =0.014) Figure 3 Frequency domain curve of drag coefficient(Re=2.03×106, Qv=0.014) |
由图 3可知,模型阻力系数变化的周期性较为明显,从功率谱密度较大可以看出,阻力系数变化的频率基本上为7.5 Hz.
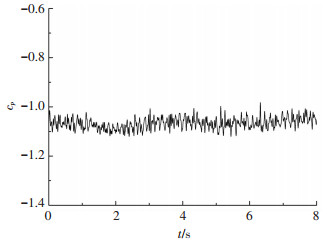
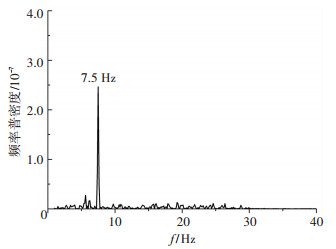
图 4、5分别给出了雷诺数Re=2.03×106、通气率Qv=0.014下尾部压力系数的时域及频域曲线.由图 4、5可知,测量时间内尾部压力系数均值基本不变,同样存在周期性脉动现象,脉动频率与模型阻力系数脉动频率相同,为7.5 Hz.模型阻力由压差阻力及摩擦阻力两部分组成,尾部压力的变化将引起模型阻力的变化,因此可认为尾部压力的周期性脉动是引起模型阻力周期性脉动的主要原因.
|
图 4 压力系数时域曲线(Re=2.03×106,Qv=0.014) Figure 4 Pressure coefficient versus time(Re=2.03×106, Qv=0.014) |
|
图 5 压力系数频域曲线(Re=2.03×106,Qv=0.014) Figure 5 Frequency domain curve of pressure coefficient(Re=2.03×106, Qv=0.014) |
图 6为Re=2.03×106,Qv=0.014时通气两相流动形态随时间变化过程,图 7为通气两相流形态图.分析可知,气体经微孔喷出,在液相剪切流速的作用下形成气液两相流动,并沿下游发展.在微孔近后方气泡表面光滑,紧贴壁面,呈细长透明形态;

|
图 6 通气两相流的非定常过程(Re=2.03×106,Qv=0.014) Figure 6 Unsteady ventilated two-phase flow(Re=2.03×106, Qv=0.014) |

|
图 7 通气两相流形态 Figure 7 Aspect graph of ventilated two-phase flow |
继续沿弹体表面向下游发展,细长透明气泡逐渐分裂成大量细碎气泡,流动区域内气泡与液相相互掺混,最终呈现均匀分布的水气两相混合状态.各时刻弹身区域气液两相流流动较为稳定,非定常特性不明显.进入尾部区域,气泡在尾部低压作用下形成回流,与液相相互掺混最终形成水气剧烈交换的云雾状模糊形态.回流区流场较为紊乱,水气混合边界呈收缩椭圆形,流动非定常特性明显,并伴有大尺度的云雾状空泡涡的断裂脱落现象,而且空泡涡的断裂脱落过程有明显的周期性.在t时刻空泡涡开始形成,并开始逐渐脱离尾部主流场的作用;在t+100 ms时刻,空泡涡完全脱落离尾部主流场,并开始沿来流方向运动.尾部流场非定常变化的过程为空泡涡脱落的准周期运动过程,脱落周期约为100 ms.
进一步分析发现,尾部涡的脱落周期与尾部压力系数脉动频率相近,因此可认为,尾部涡的周期性脱落引起尾部压力系数产生周期性脉动现象,继而导致模型阻力系数出现周期性脉动.
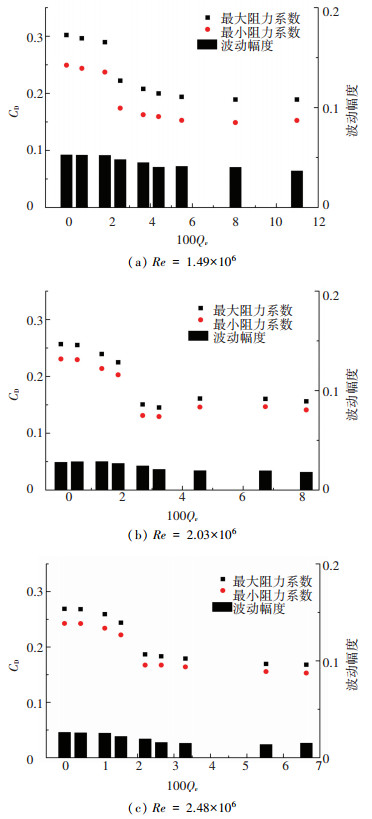
2.2 流动参数对水动力脉动特性影响图 8给出了Re=1.49×106、2.03×106、2.48×106下,模型阻力系数的波动范围随通气率的变化过程.
|
图 8 阻力系数波动范围 Figure 8 Fluctuating scale of drag coefficient |
图中波动幅度为最大阻力系数及最小阻力系数之差.由图 8可知,3种雷诺数下阻力系数脉动变化规律一致,存在饱和通气率;随着通气率的增加,模型阻力系数平均值下降,波动范围减小,直至饱和通气率;此后,继续增加通气率,阻力系数均值及其波动范围变化不明显.进一步分析发现,Re=1.49×106时,未通气下的阻力系数波动幅度及饱和通气率下的阻力系数波动幅度分别为0.053及0.040,Re=2.03×106时分别为0.028及0.019,Re=2.48×106时分别为0.026及0.016,由此可知雷诺数的增加将使阻力系数波动幅度降低.综上分析,通气率及雷诺数的增加都将降低模型阻力系数的波动幅度.进一步分析认为,通气率及雷诺数的增加使得两相流的不稳定性增加,模型尾部湍流掺混增强,从而引起尾部绕流分离点向下游移动,使得尾部回流区减弱,继而降低了阻力系数的脉动幅度,这与经典的流动分离理论相似.
图 9给出了Re=1.49×106、2.03×106、2.48×106下,模型阻力系数脉动频率随通气率的变化特性.

|
图 9 阻力系数脉动频率随通气率变化的曲线 Figure 9 Drag-fluctuating frequency versus air entrainment coefficient at Re=1.49×106, 2.03×106, 2.48×106 |
从图 9(a)可知,当Re=1.49×106时,各通气率下的阻力系数脉动的周期性较为明显,这从功率谱密度较大可以看出,随着通气率的增加,阻力系数脉动频率恒定保持为5.5 Hz.由图 9(b)、(c)可知,随着雷诺数的增加,阻力系数脉动的周期性有所减弱,而其脉动频率随通气率的变化始终保持为恒定值,Re=2.03×106及2.48×106下的脉动频率分别为7.5及10.0 Hz.因此认为,通气率的改变对模型阻力系数的脉动频率无明显影响,而雷诺数的增加将使阻力系数脉动频率增加.分析认为尾部空泡涡的形成、脱落是由于尾部出现间断面,引起气液两相流动在尾部分离而出现回流区,继而形成起始空泡漩涡;流体的不断补充使得起始漩涡逐渐变大,并在主流作用下开始脱落,同时在分离点又形成新的空泡漩涡.由于阻力系数的脉动是涡的周期性脱落引起的,故可认为通气率对涡的脱落周期无明显影响,涡的脱落频率随雷诺数的增加而增加,这与经典的圆柱涡脱落理论相符.
3 结论1) 描述了典型工况下通气两相流的流动过程,弹身区域流场呈均匀分布的水气两相混合状态,流动稳定,非定常特性不明显;尾部区域流场较为紊乱,非定常特性明显,尾部空泡涡的周期性脱落引起模型阻力系数出现周期性脉动现象.
2) 绕流线型回转体通气两相流动的非定常特性与雷诺数及通气率有关.通气率的增加可降低由于尾部涡的脱落而引起的阻力系数的波动幅度,而对尾部涡的脱落频率无明显影响;随着雷诺数的增加,由于尾部涡的脱落而引起的阻力系数的波动幅度减小,尾部涡的脱落频率增加.
| [1] | WU S J, OUYANG K, SHIAH S W. Robust design of microbubble reduction in a channel flow using the Taguchi method[J]. Ocean Engineering, 2008, 35(8): 856-863. DOI: 10.1016/j.oceaneng.2008.01.022 |
| [2] | MCCORMICK M E, BHATTACHARYA R. Drag reduction of a submersible hull by electrolysis[J]. Naval Engineers Journal, 1973, 85(2): 11-16. DOI: 10.1111/j.1559-3584.1973.tb04788.x |
| [3] | MAVAN N K, DEUTSCH S, MERKLE C L. Reduction of turbulent skin friction by microbubble[J]. Physics of Fluids, 1984, 27(2): 356-368. DOI: 10.1063/1.864620 |
| [4] | JINHO J, CHOI S H, KIM B, et al. Experiment investigation of frictional resistance reduction with air layer on the hull bottom of a ship[J]. Ocean Engineering, 2014, 6(2): 363-379. DOI: 10.2478/IJNAOE-2013-0185 |
| [5] | YOSHIAKI K, TAKAHITO T. Experimental study on microbubbles and their applicability to ships for skin friction reduction[J]. International Journal of Heat and Fluid Flow, 2000, 21(5): 582-588. DOI: 10.1016/S0142-727X(00)00048-5 |
| [6] | KATO H. Experimental study on microbubble injection method for frictional drag reduction[J]. Journal of Marine Science and Technology, 1998, 3(3): 122-129. DOI: 10.1007/BF02492919 |
| [7] | KATO H, MIYANAGA M, HARAMOTO Y, et al. Frictional drag reduction by injecting bubbly water into turbulence boundary layer [C]//ASME Fluids Engineering Division summer meeting. New York: ASME, 1994 : 185-194. |
| [8] | OUYANG K, WU S J, HUANG H H. Optimum parameter design of microbubble drag reduction in a turbulent flow by the Taguchi me-thod combined with artificial neural networks[J]. Journal of Fluids Engineering, 2013, 135(11): 1-11. DOI: 10.1115/1.4024930 |
| [9] | DEUTSCH S, CASTANO J. Microbubble skin reduction on an axisymmetric body[J]. Physics of Fluids, 1986, 29(11): 3590-3597. DOI: 10.1063/1.865786 |
| [10] | CLARK H, DEUTSCH S. Microbubble skin reduction on an axisymmetric body under the influence of applied axial pressure gradients[J]. Physics of Fluids A, 1991, 3(12): 2948-2954. DOI: 10.1063/1.857837 |
| [11] | SANDERS W C, WINKEL E S, DOWLING D R, et al. Bubble friction drag reduction in a high-Reynolds-number flat-plate turbulent boundary layer[J]. Journal of Fluid Mechanics, 2006, 552: 353-380. DOI: 10.1017/S0022112006008688 |
| [12] | ELBINGL B R, WINKEL E S, LAY K S, et al. Bubble-induced skin-friction drag reduction and the abrupt transition to air-layer drag reduction[J]. Journal of Fluid Mechanics, 2008, 612: 201-236. DOI: 10.1017/S0022112008003029 |
| [13] |
董文才, 周晨, 张军. 回转体气层减阻降噪模型试验研究[J].
海军工程大学学报, 2011, 23(3): 5-9.
DONG Wencai, ZHOU Chen, ZHANG Jun. Gyrodidal model experiment on resistance and noise reduction by bubble layer[J]. Journal of Naval University of Engineering, 2011, 23(3): 5-9. DOI: 10.3969/j.issn.1009-3486.2011.03.002 |
| [14] |
傅慧萍. 平板微气泡减阻数值模拟及影响因素分析[J].
哈尔滨工程大学学报, 2015, 36(10): 1297-1302.
FU Huiping. Numerical simulation of microbubble drag reduction in a plate and factors in fluencing its practicality process[J]. Journal of Harbin Engineering University, 2015, 36(10): 1297-1302. DOI: 10.11990/jheu.201407002 |
| [15] |
傅慧萍, 李杰. 微气泡减阻的数值模拟方法及尺寸效应[J].
上海交通大学学报, 2016, 50(2): 278-282.
FU Huiping, LI Jie. Numerical simulation of micro-bubbles drag reduction and scale effect[J]. Journal of Shanghai Jiao Tong University, 2016, 50(2): 278-282. DOI: 10.16183/j.cnki.jsjtu.2016.02.020 |
| [16] |
王威. 通气参数对水下航行体流体动力影响[D]. 哈尔滨: 哈尔滨工业大学, 2013.
WANG Wei. Experimental research on effect of ventilation parameters on hydrodynamic characteristic of under water vehicle [D]. Harbin: Harbin Institute of Technology, 2013. |
 2017, Vol. 49
2017, Vol. 49


