中国大部分城市供水管网漏失率居高不下,许多供水单位为满足管网末端最不利点的用水压力需求直接对管网进行加压,并未对沿途管网采取有效的降压及保护措施,导致陈旧的管网不堪重负,爆管现象频发,漏损现象严重,水质易受到污染,导致饮用水卫生安全隐患.而采取智能减压阀是当今减缓漏损情况的有力手段,如何在铺设减压阀前根据不同的位置及开度对减压效益进行评估,从而确定最优决策一直是需要解决的问题.
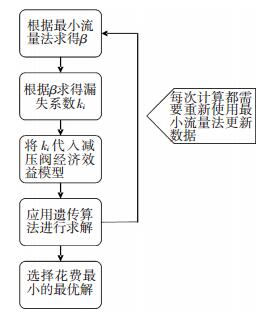
本文提出的减压阀经济效益模型如图 1所示.
|
图 1 减压阀经济效益模型求解流程 Figure 1 Flow chart for economic benefit model of reducing valves |
传统压力驱动节点流量模型[1]中节点流量为节点实际用水量与节点漏失量之和,需分别计算二者再叠加,可以更精确地反映管网实际运行工况,但存在复杂度太大的问题,增加了计算时间.在节点用水量受压力影响较小的情况下,本文假定用水量与压力无关,从而获得更加简洁实用的改进压力驱动漏失水力模型.
对于压力优化控制分析,需要建立一个包含压力相关漏失量的改进水力模型.漏失量通常分为背景漏失和爆管两类.其中背景漏失代表管段、接头和连接件等处产生的渗漏,取决于管道的服务压力,因此,压力控制的目的就是要减少这一部分的漏失.近年来,国内外学者通过大量的实验数据,得出了许多漏失量与管网服务压力间的数学模型[2-5].在估计出管网背景漏失总量的大概值后,为了确保模型的准确性需要将其按照比例分配至管网水力模型的每个节点上.根据实际工程经验,在接头和连接件处最容易发生漏失,故背景漏失量分配标准按照各节点流量(或用户连接数)比例制定.
节点漏失与压力间的经验关系式如式(1) 所示.该式将被添加到标准的管网水力平衡方程式中,以形成一个适于压力控制和漏失分析的拓展水力模型
| $ l\left( t \right) = k \cdot p{\left( t \right)^\alpha } = k \cdot {\left( {h\left( t \right)-H} \right)^\alpha }. $ | (1) |
式中:l(t)为t时刻的节点漏失量, p(t)为节点压力, h(t)为总水头, k为漏失系数, α为漏失指数, H为节点高程.
假定漏失只在有流量的节点上产生,将这些节点记作Id.经大量实验证明,漏失指数α的影响因素包括管材、漏失类型和土质等,其取值一般在0.5~2.5[6-8].
结合HJ分区实际情况,根据文献中的建议,本文取α为常数1.18[9],而漏失系数ki取决于各节点的流量,可通过夜间最小流量法[1, 10]得出.
夜间最小流量法一般取凌晨2~4点的夜间流量,由于此时用户用水量处于全天最低点,漏损量所占比例最大,因此,根据夜间最小流量计算出来的漏失系数较为准确.
根据英国水道协会(WRC)长期研究结果,夜间居民的平均用水量为1.7 L/(户·h),则可得夜间最小流量时刻的管网漏失量计算公式为
| $ q\left( {{t_{\min }}} \right) = Q\left( {{t_{\min }}} \right)-0.0017 \times 用户数. $ | (2) |
式中:q(tmin)为夜间最小流量时刻的漏失量,m3/h;Q(tmin)为夜间最小流量,m3/h.
夜间最小流量时刻的漏失量等于各节点漏失量之和, 即
| $ q\left( {{t_{\min }}} \right) = \sum\limits_{i \in {I_d}} {{l_i}\left( {{t_{\min }}} \right)} = \sum\limits_{i \in {I_d}} {{k_i} \cdot {p_i}{{\left( {{t_{\min }}} \right)}^{1.18}}} . $ | (3) |
式中pi(tmin)为夜间最小流量时刻的节点压力,m.
假定漏失量与节点流量成正比[11],引入比例因子β,各节点的漏失系数ki计算如下:
| $ {k_i} = \beta \cdot {d_i}\left( {{t_{\min }}} \right), $ | (4) |
式中di(tmin)为夜间最小流量时刻的节点流量,m3/h.
综合式(3)、(4) 得
| $ q\left( {{t_{\min }}} \right) = \sum\limits_{i \in {I_d}} {{l_i}\left( {{t_{\min }}} \right)} = \sum\limits_{i \in {I_d}} {\beta \cdot {d_i}\left( {{t_{\min }}} \right) \cdot {p_i}{{\left( {{t_{\min }}} \right)}^{1.18}}} . $ | (5) |
由于在该模型中,夜间最小流量时刻的节点流量和压力均已知,该比例因子β可由式(6) 估计得到:
| $ \beta = \frac{{q\left( {{t_{\min }}} \right)}}{{\sum\limits_{i \in {I_d}} {{d_i}\left( {{t_{\min }}} \right) \cdot {p_i}{{\left( {{t_{\min }}} \right)}^{1.18}}} }}. $ | (6) |
求得β后,分区内每条管段的漏失系数ki即可求得.
以EPANET 2.0平台进行微观水力模拟,算得各节点的漏失系数后,通过MATLAB软件编写程序将这些漏失系数值导入EPANET中,即可得到拓展的压力驱动漏失水力模型.
2 减压阀经济效益模型减压阀[12]控制方式一般有固定出口压力控制、基于时间调节出口压力控制、基于流量调节出口压力控制以及基于最不利点的出口压力闭环控制,考虑到DMA分区属于三级分区,本文采用固定出口压力控制,即将阀门开度设置为固定值,运行维护方便且十分低廉.
一般减压阀的服役寿命为15 a,优化的目标是在给定投资费用收回年限和给定最大允许漏损量以及保证管网最不利点满足最小压力需求的前提下,寻找减压阀的最优安装位置、开度及安装数量.
2.1 目标函数该模型目标函数是安装减压阀后年平均利润最大,即
| $ \max f = \frac{{15 \times 365c\left( {{q_{{\rm{leak}}}}-{f_1}} \right)-{f_2}}}{{15}}. $ | (7) |
式中:f为15 a内年平均利润;c为单位水价,取0.6元/m3;qleak为未安装减压阀前分区的总漏损量,m3/d;f1为安装减压阀后分区的总漏损量,m3/d;f2为减压阀投资成本,元.
| $ {f_1} = \sum\limits_{i \in {I_b}} {{l_i}\left( t \right)} = \sum\limits_{i \in {I_b}} {{k_i}{p_i}{{\left( t \right)}^{1.18}}}, t \in T. $ | (8) |
式中:li(t)为t时刻分区入口节点i的漏失量,m3/h;Ib为入口节点集合;T为时间段序列.
| $ {f_2} = \sum\limits_{j = 1}^n {{c_j}} . $ | (9) |
式中cj为第j个减压站的投资费用,元.
国产200X减压阀具体投资费用见表 1.
| 表 1 国产200X减压阀具体投资费用 Table 1 Investment cost of 200X pressure reducing valve from China |
此外,安装费、现场测试费、减压阀维护费用等其他费用为8 000元/个.
2.2 约束条件 2.2.1 最大允许漏失量率约束| $ \frac{{{l_i}}}{Q} < {R_{{\rm{AL}}}}. $ | (10) |
式中:li为所有节点全天(24 h)漏失总流量,m3/h;Q为总流量,m3/h;RAL为最大允许漏失率.
2.2.2 水力平衡约束管网水力平衡约束包括管段压力损失方程(闭合环路水头损失为0) 和节点流量连续方程,如式(11)、(13) 所示:
| $ \sum\limits_{i \in {\rm{loop}}} {\Delta {h_i} = 0} . $ | (11) |
式中Δhi为环路中管段水头损失.
| $ {h_{ij}} = 10.667C_{ij}^{-1.852}{\left( {{k_{ij}}{d_{ij}}} \right)^{-4.871}}{L_{ij}}Q_{ij}^{1.852}. $ | (12) |
式中:hij为节点i和j之间的管道水头损失,m;Cij为管道粗糙系数;kij为节点i和j之间管道的减压阀开度,取值为0~1;dij为节点i和j之间的管道直径,m;Lij为节点i和j之间的管道长度,m;Qij为节点i和j之间的管道流量,m3/h.
| $ \sum\limits_{\begin{array}{*{20}{c}} {j = 1}\\ {j \ne i} \end{array}}^n {{q_{ij}}-{d_i}-{l_i}} = 0. $ | (13) |
式中:qij为节点i相连管道的流量,m3/h;di为节点i用水量,m3/h;li为节点i漏失量,m3/h.
2.2.3 节点压力约束各节点供水压力既要满足最小服务水头,又不能过高造成不必要的能源浪费,即
| $ {h_{i, \min }} \le {h_i} \le {h_{i, \max }}. $ | (14) |
式中节点压力的上下限hi, min和hi, max依据节点类型和实际情况具体定值,必须保证最不利点压力的最小服务水头,其他节点可相对宽松.
2.2.4 减压阀数量约束| $ n \le {N_v}, $ | (15) |
式中Nv为减压阀最大安装数量.
2.2.5 投资费用回收年限约束| $ y \le 2, 即2 \times 365c\left( {{q_{{\rm{leak}}}}-{f_1}} \right) \ge {f_2}, $ | (16) |
式中y为费用回收年限,a.
则管网减压阀优化控制问题具体表示为
| $ \max f = \frac{{5475c\left( {{q_{{\rm{leak}}}}-{f_1}} \right)-{f_2}}}{{15}}. $ |
其中
| $ \begin{array}{*{20}{c}} {{f_1} = \sum\limits_{i \in {I_b}} {{l_i}\left( t \right)} = \sum\limits_{i \in {I_b}} {{k_i}{p_i}{{\left( t \right)}^{1.18}}}, t \in T, }\\ {{f_2} = \sum\limits_{j = 1}^n {{c_j}} .} \end{array} $ |
subject to:
| $ \begin{array}{*{20}{c}} {\sum\limits_{\begin{array}{*{20}{c}} {j = 1}\\ {j \ne i} \end{array}}^n {{q_{ij}}-{d_i}-{l_i}} = 0, }\\ {\sum\limits_{i \in {\rm{loop}}} {\Delta {h_i} = 0}, } \end{array} $ |
| $ \begin{array}{*{20}{c}} {{h_{ij}} = 10.667C_{ij}^{-1.852}{{\left( {{k_{ij}}{d_{ij}}} \right)}^{-4.871}}{L_{ij}}Q_{ij}^{1.852}, }\\ {\frac{{{l_i}}}{Q} < {R_{{\rm{AL}}}}, }\\ {{h_{i, \min }} \le {h_i} \le {h_{i, \max }}, }\\ {n \le {N_v}, }\\ {2 \times 365c\left( {{q_{{\rm{leak}}}}-{f_1}} \right) \ge {f_2}.} \end{array} $ |
为了求解该减压阀优化控制模型,采用遗传算法[13].遗传算法主要包括染色体编码、适应度选择、交叉、变异.
3.1 染色体编码该模型决策变量为减压阀位置(位于哪个管道ID上)以及开启状态下每个时间段下的开度,浮点数编码.值得注意的是,如果减压阀开度为1,表明该管道未安装减压阀.每条染色体包括所有管道减压阀铺设位置以及开度信息.
3.2 适应度选择为了减少运算量,适应度函数取
个体能否被保留复制至下一代采用轮盘赌方式进行随机选择,即
| $ 1-{P_i} = \frac{{{f_i}}}{{\sum\limits_{i = 1}^n {{f_i}} }}. $ | (17) |
式中:Pi为该染色体被保留的概率;fi为该染色体的目标函数值,即漏失量,m3/h;
从而,每条染色体被选择的方式得以建立.
3.3 交叉一组染色体(浮点数)交叉的规则是构造0~1之间的随机数α和β,对于一对染色体ch1和ch2,通过交叉后得到ch1′和ch2′,满足以下关系:
| $ \left\{ \begin{array}{l} {\rm{ch1' = }}\left( {1-\alpha } \right){\rm{ch1 + }}\beta {\rm{ch2, }}\\ {\rm{ch2' = }}\left( {1-\beta } \right){\rm{ch1 + }}\alpha {\rm{ch2, }}\\ {\rm{ch2' = }}L\left( {{\rm{If}}\;{\rm{ch2'}} \le L} \right), \\ {\rm{ch1' = }}L\left( {{\rm{If}}\;{\rm{ch1'}} \le L} \right), \\ {\rm{ch2' = }}R\left( {{\rm{If}}\;{\rm{ch2'}} \ge R} \right), \\ {\rm{ch1' = }}R\left( {{\rm{If}}\;{\rm{ch1'}} \ge R} \right). \end{array} \right. $ |
式中L、R分别代表定义区间的上下确界.
3.4 变异变异是针对开度非1的减压阀(即管道存在减压阀),将原有开度随机变成(0~1) 的任意开度.
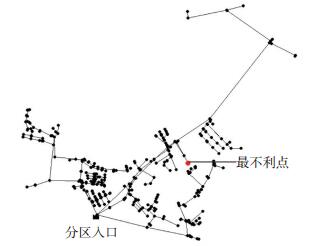
4 算例模拟算例取自文献[1]中的HJ分区模型,具体参数可参考原文,管网拓扑如图 2所示,部分参数见表 2.
|
图 2 HJ分区管网拓扑结构 Figure 2 HJ Partition network topology structure |
| 表 2 HJ分区管网参数 Table 2 HJ Partition network parameters |
该分区共有623个节点,其中329个节点有流量,每次使用遗传算法模拟减压阀位置及开度时,均需要重新使用夜间最小流量法计算β和ki,即将夜间最小流量法内置于遗传算法内.管段管径均位于300 mm之下,且存在大量管径小于100 mm的管段,管段具体管径参考文献[13].迭代次数取100次.
4.1 编码为了减少计算量,对算法进行优化,假定减压阀仅设在管径较大的100条管段上,其他小管径或者枝状管网末端不考虑安装减压阀,则染色体长度为100位,分别代表100个管段ID对应的减压阀开度,样本个数取200个,每个样本有且仅有一个单位非1,且每个管段ID所对应的同一阀门(非1) 位置只有两条染色体表示(代表200种情况,每种情况有且只有一个减压阀安装在对应的管道ID上,同时可以保证每个管段上安装阀门有不同的开度情况,方便交叉变异时进行保留),所安装的减压阀开度随机在(0~1) 取值.这200个个体作为初始种群P0.
4.2 选择将100个个体代入目标函数,由于全天各时段的每个节点压力和管道流量已知,可以求得各自的漏损量及漏损率.如果此时有满足漏损率 < 7%的情况出现,将其输出至资源库.如果有压力不满足18 m最小水头,或阀门个数超过2个的情况,直接将其从资源库剔除.使用轮盘赌方法选择100条染色体,构成种群Ri(i为代数).
4.3 交叉变异对种群Ri的染色体进行交叉变异操作.交叉是将100条染色体随机分成50对,每对进行交叉,如果是同一位置的减压阀进行交叉,该染色仍然只有一个减压阀,减压阀位于不同位置的染色体交叉,则会产生两个减压阀.为满足减压阀最大个数为2的要求,设定当染色体非1位置为2时,只能与同一位置的染色体交叉.交叉概率取80%.
变异则是随即改变非1位置的数字,范围为(0~1),0和1不能取,变异概率取5%.
通过交叉变异后得到100条新的染色体Qi,与Ri合并,得到种群Pi+1.
再进行4.2的选择操作,循环至100次的迭代次数为止.
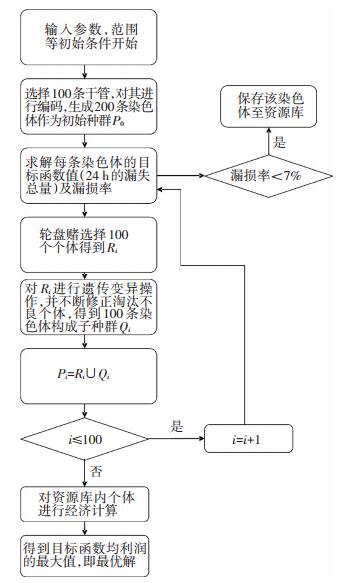
最后对资源库的染色体进行筛选,年均利润最大的染色体就是所需的最优解.流程图如图 3所示.
|
图 3 求解HJ分区遗传算法流程 Figure 3 Genetic algorithm flow chart for HJ partition solution |
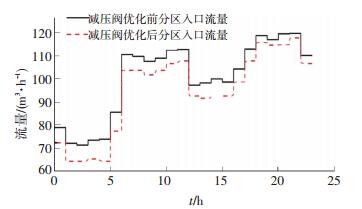
在满足漏损率低于7%及投资费用两年回收的前提下,应用减压阀经济效益模型对HJ分区管网进行求解,最终最优解为在管段分区入口处设置一个减压阀,开度0.2为该算例的最优解.优化前后分区入口流量变化见图 4.
|
图 4 HJ分区减压阀优化控制前后入口流量 Figure 4 Partition pressure reducing valve inlet flow before and after optimization control |
该管网在正常工况下总流量为496.75 L/s,未设置减压阀时的管网漏失量为60.11 L/s,经减压阀优化控制后的漏失量为32.78 L/s,漏失率由12.1%最多可下降至6.6%,满足了漏损率低于7%的要求;减压阀投资费用为40 465元,每年可节约因漏损造成的水费517 127元,3个月即可回收成本;安装减压阀带来的年平均利润为514 430元.
5 结论1) 本文根据压力驱动漏失水力模型结合夜间最小流量法,确定管网节点的漏失系数,代入遗传算法内,从而建立考虑压力引起漏失量的改良水力模型.
2) 传统遗传算法对全管网进行减压阀位置和开度的优化时,得到的结果往往因设置阀门数量过多而缺乏实际意义,本文中经济效益模型则以经济实用性对实际进行衡量.
3) 将减压阀优化控制模型应用到算例管网中,证明了该模型理论的可行性和实用性.
4) 由于算例中最大安装减压阀个数较少,本文中算法比较适用于DMA分区中确定减压阀相关信息.
| [1] |
乔怡超. 供水管网减压阀优化控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.
QIAO Yichao.Research on leakage control of water distribution system by on presure reducing valves[D]. Harbin: Harbin Institute of Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10213-1014083246.htm |
| [2] |
董深, 吕谋, 盛泽斌, 等. 基于遗传算法的供水管网反问题流失定位[J].
哈尔滨工业大学学报, 2013, 45(2): 106-128.
DONG Shen, LV Mou, SHENG Zebin, et al. Inverse transient leakage location of water supply network based on genetic algorithm[J]. Journal of Harbin Institute of Technology, 2013, 45(2): 106-128. DOI: 10.11918/j.issn.0367-6234.2013.02.019 |
| [3] |
GIUSTOLISI O, SAVIC D, KAPELAN Z. Pressure-driven demand and leakage simulation for water distribution networks[J].
Journal of Hydraulic Engineering, 2008, 134(5): 626-635.
DOI: 10.1061/(ASCE)0733-9429(2008)134:5(626) |
| [4] |
SHAMMAS N K, KHALED H. Effect of pressure on leakage rate in water distribution networks[J].
Methods, 1993.
|
| [5] |
NOACK C, ULANICKI B. Modeling of soil defensibility on leakage characteristics of buried pipes[C]//8th Annual Water Distribution Systems Analysis Symposium. Cincinnati, Ohio, USA, 2006.
https://www.researchgate.net/publication/268601954_Modelling_of_Soil_Diffusibility_on_Leakage_Characteristics_of_Buried_Pipes
|
| [6] |
THORNTON J, LAMBERT A. Progress in practical prediction of pressure: Leakage, pressure: Burst frequency and pressure: Consumption relationships[C]//Proceedings of IWA Special Conference 'Leakage 2005'. Halifax, Nova Scotia, Canada, 2005.
https://www.researchgate.net/publication/228362731_Progress_in_practical_prediction_of_pressure_leakage_pressure_burst_frequency_and_pressure_consumption_relationships
|
| [7] |
ULANICKI B, PRESCOTT S L. Anatomy of leakage[C]//Unpublished Notes Available from Process Control-Water Software Systems. The Gateway, Leicester, LE1 9BH, UK: De Montfort University, 2006.
|
| [8] |
WU Z Y, SAGE P, TURTLE D. Pressure-dependent leak detection model and its application to a district water system[J].
Journal of Water Resources Planning & Management, 2010, 136(1): 116-128.
|
| [9] |
高金良, 李娟娟, 郑成志, 等. 区域供水管网盲源分离漏失量研究[J].
哈尔滨工业大学学报, 2015, 47(6): 33-37.
GAO Jinliang, LI Juanjuan, ZHENG Chengzhi, et al. Study on leakage of regional distribution network using blind source separation[J]. Journal of Harbin Institute of Technology, 2015, 47(6): 33-37. DOI: 10.11918/j.issn.0367-6234.2015.06.006 |
| [10] |
陈迪超, 奚卫红, 江标初. 供水管网主动漏损控制方法与管理流程[J].
中国给水排水, 2015, 31(18): 11-13.
CHEN Dichao, XI Weihong, JIANG Biaochu. Study on active control and management for water supply networks[J]. China Water & Wastewater, 2015, 31(18): 11-13. |
| [11] |
马悦, 高金良. 管网供水压力与漏失量关系研究[J].
供水技术, 2013, 7(5): 15-18.
MA Yue, GAO Jinliang. Study on the relations of water supply pressure and leakage[J]. Water Technology, 2013, 7(5): 15-18. |
| [12] |
黄钢, 金涛, 周泽渊. 协同进化遗传算法在减压阀优化配置中的应用[J].
计算机与数字工程, 2014, 42(1): 36-40.
HUANG Gang, JIN Tao, ZHOU Zeyuan. Application of co-evolutionary genetic algorithm in optimal pressure reducing valve placement[J]. Computer & Digital Engineering, 2014, 42(1): 36-40. |
| [13] |
LING S H, LEUNG F H F. An improved genetic algorithm with average-bound crossover and wavelet mutation operations[J].
Soft Computing, 2007, 11(11): 7-31.
|
 2017, Vol. 49
2017, Vol. 49


