2. 华侨大学 土木工程学院, 福建 厦门 361021
2. College of Civil Engineering, Huaqiao University, Xiamen 361021, Fujian, China
城市供水管网漏失不仅会造成宝贵水资源的浪费和严重的经济损失,还会引发严重的社会问题,如道路、地基下沉[1]等,潜在危害极大.因此,研究供水管网漏失问题并最终找到控制解决办法是极其重要且迫切的任务.管网漏失控制的一个重要前提是较准确地计算出管网漏失量[2].当前国际上常用的计算漏失量的方法包括夜间最小流量法、水平衡分析法和基于管网漏失量水力模型的分析法.夜间最小流量法[3]简单易行,但是该方法过分依赖主观经验而缺乏理论支撑,导致判断结果的精确度与可信度不高.水平衡分析法[4]通常包括依赖统计数据推算而得的表观漏失水量和免费供水量,数据的准确性不足.基于管网漏失量水力模型的分析法,具有较强的漏失辨识能力,但是模型中参数的确定多是依赖经验取值,导致模型内核存在一定缺陷.此外,李文博[5]将灰色关联动态分析理论应用于供水管网的漏失量化研究中,该研究侧重于管网漏失控制工作方面,并未提出量化漏失量的具体方法.高金良等[6]尝试用盲源分离理论来研究管网漏失量,具有一定创新性,但也难以摆脱幅值不确定性的问题.
本研究利用Kalman滤波算法,构建并求解供水管网系统漏失数学模型,并在实验室漏失模拟平台上进行实验,对比分析模型模拟计算的漏失量和实测的真实漏失量数据,验证了该模型算法的可行性与可靠性,为控制漏失工作做好了准备.
1 Kalman滤波算法简介Kalman滤波[7]由匈牙利数学家卡尔曼(R.E.Kalman)于1960年正式提出,随后被广泛应用于各个领域,这是因为它具有其他滤波无法比拟的优势:采用的算法具有实时递推性,即最优化自回归数据处理算法[8];在分析随机过程估计问题时,卡尔曼将状态空间方法灵活地融入进时域中,提高了解决问题的效率.
Kalman滤波处理的对象是随机信号[9].首先利用一定的先验信息,以系统的观测信号为输入,以所求信号的估计值为输出,将基本问题描述为一个函数,即观测方程
| $ x = f\left( {s, v} \right). $ | (1) |
式中:x表示观测信号向量;s表示源信号向量,也是拟估计的状态参数;v表示系统过程噪声.
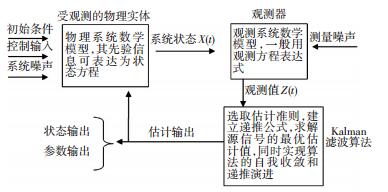
然后以观测方程为约束,以合适的估计准则为目标函数,求出待求状态参数的最优值[10],这就是Kalman滤波算法的应用思路.通常来讲,我们所了解的先验信息,是系统的内部特性和系统状态量的变化规律,一般表达为系统的状态方程.所以,建立合理的状态方程和观测方程是正确应用Kalman滤波算法的前提.Kalman滤波算法的工作原理如图 1所示.
|
图 1 Kalman滤波算法工作原理 Figure 1 Kalman filtering system schematic diagram |
在管网总供水量和用户总用水量均已知时,两者之差即为所求的管网漏失量.管网总供水量一般较容易计算,本研究利用Kalman滤波算法计算实际操作中难以准确测定的用户总用水量.供水管网系统实际上是一个连续的随机动态系统,必须先将其离散化才能使用Kalman滤波算法,本研究以稳定的运行状态为判断依据按照时间段将其分割离散.然后建立关于所求状态参数的状态方程与观测方程,最后依据估计准则建立关于最优解的递推公式,从而求出待求状态参数的最优估计值,同时实现算法的递推运算和自我收敛.
2.1 建立状态方程在供水管网系统中提取关于所求状态参数的先验信息,建立状态方程:以所求的状态量即当前时刻的用户用水量估计值为因变量,以前一时刻的用户用水量估计值为自变量,并引入系统的控制输入量以及系统过程噪声,建立系统的状态方程
| $ X\left( k \right) = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}X\left( {k-1} \right) + \mathit{\boldsymbol{B}}U\left( k \right) + W\left( k \right). $ | (2) |
式中:X(k)表示k时刻管网中的用水量;U(k)表示k时刻对管网的控制输入;Φ为状态转移矩阵,反映管网运行状态的变化情况;B表示与控制输入相关的矩阵;W(k)表示过程噪声.
2.2 建立观测方程确定Kalman滤波算法的约束条件:以与用户用水量相关的观测信号为输入,以所求用户用水量的估计值为输出,建立供水管网系统的观测方程
| $ Z\left( k \right) = \mathit{\boldsymbol{H}}X\left( k \right) + V\left( k \right). $ | (3) |
式中:Z(k)表示k时刻与用户用水量相关的观测信号;X(k)表示k时刻管网中的用水量;H为测量矩阵,表示用户用水量与观测信号的内在关系;V(k)表示测量噪声.
2.3 目标函数及最优解的计算本研究拟采用管网用户用水量的线性最小方差估计为估计准则,也是求解最优解的目标函数,确定Kalman滤波算法的求解过程如下
1) 在管网上一运行状态K-1的基础上,结合管网系统的过程模型,对管网下一状态K的用水量进行预测,计算公式为
| $ \hat X\left( {k\left| {k-1} \right.} \right) = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\hat X\left( {k-1\left| {k-1} \right.} \right) + \mathit{\boldsymbol{B}}U\left( k \right). $ | (4) |
式中:
2) 同时,需更新对应于
| $ \mathit{\boldsymbol{P}}\left( {k\left| {k-1} \right.} \right) = \mathit{\boldsymbol{ \boldsymbol{\varPhi} P}}\left( {k-1\left| {k-1} \right.} \right){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}} + {Q_{k - 1}}. $ | (5) |
式中:P(k|k-1) 表示状态X(k|k-1) 所对应的误差方差阵,P(k-1|k-1) 表示状态X(k-1|k-1) 所对应的误差方差阵,ΦT表示状态转移矩阵的转置矩阵, Qk表示系统过程噪音.式(4) 和(5) 即为对供水管网系统的预测.
3) 为了将管网系统在状态K下的预测用水量最优化,需要结合用水量预测值
| $ \hat X\left( {k\left| k \right.} \right) = \hat X\left( {k\left| {k-1} \right.} \right) + {K_k}\left( {Z\left( k \right)-X\left( {k\left| {k-1} \right.} \right)} \right). $ | (6) |
式中:Z(k)表示k时刻与管网用水量相关的测量值,Kk为卡尔曼最优滤波增益.
4) 估计准则为用户用水量满足线性最小方差估计,卡尔曼最优滤波增益计算公式如下
| $ {K_k}\mathit{\boldsymbol{ = P}}\left( {k\left| {k- 1} \right.} \right)\mathit{\boldsymbol{H}}_k^{\rm{T}}{\left[{{\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{P}}\left( {k\left| {k-1} \right.} \right)\mathit{\boldsymbol{H}}_k^{\rm{T}} + {\mathit{\boldsymbol{R}}_k}} \right]^{ -1}}. $ | (7) |
式中:Rk表示V(k)的正定方差矩阵,Hk表示k时刻的测量矩阵,HkT表示测量矩阵的转置矩阵.
5) 通过上述运算,可得到管网系统在状态K下用水量的最优估计结果,为了使Kalman滤波算法能够实时递推,持续进行,需要同时更新K状态时
| $ \mathit{\boldsymbol{P}}\left( {k\left| k \right.} \right) = \left( {\mathit{\boldsymbol{I}}-K_k{\mathit{\boldsymbol{H}}_k}} \right)\mathit{\boldsymbol{P}}\left( {k\left| {k-1} \right.} \right). $ | (8) |
其中I为1的矩阵,只有当模型为单模型且只有唯一状态量时,I=1.系统进入K+1状态时P(k|k)即为式(4) 的P(k-1|k-1).如此,算法便能实现自回归运算.
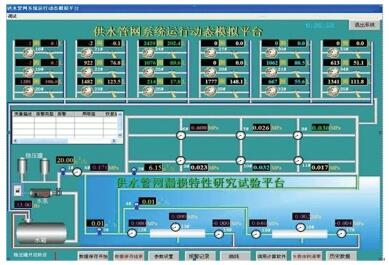
3 管网漏失模拟实验验证Kalman滤波算法由于在现场难以准确测定不同工况下的用户用水量和管网漏失量,采用在实验室中进行模拟实验,用不同的阀门开启度和水表计量的方法来模拟管网用户用水量和管网漏失量.通过水表计量的方式进行模拟,一部分水表模拟管网中用户用水量,另一部分水表模拟管网中的漏失量.用人工调节水泵运行频率的方法模拟管网的不同运行工况.在管网系统某一稳定运行的工况下,实验模拟管网发生漏失时的情况,记录各项参数,包括水泵出口流量、管网入口流量、管网总供水量、用户总用水量、管网漏失量等,然后改变运行工况与实验条件,记录参数的变化情况,建立管网系统的状态方程与参数方程,采用Kalman滤波算法并结合相关实验数据,计算出管网中用户用水量的变化情况,最后利用差值法求出管网漏失量.实验平台如图 2所示.
|
图 2 管网漏失模拟系统 Figure 2 Pipeline leakage simulation system diagram |
在建立准确的管网系统漏失数学模型的过程中,对于管网系统过程噪声和观测噪声相关统计特性的收集往往存在较大困难,故需作如下假设:供水管网系统中的过程噪声序列W(k)和观测噪声序列V(k)均为高斯白噪声随机序列,且均值为零;Qk为非负定方差矩阵;Rk为正定方差矩阵;W(k)和V(k)二者相互独立,且均与管网初始运行状态无关.
3.1.2 状态方程的建立状态量为每一稳定工况下模拟的管网中用户用水量及其随时间变化的变化量,即
| $ {X_k}\left( {\begin{array}{*{20}{c}} {{Q_k}}\\ {{a_{{Q_k}}}} \end{array}} \right), k = 0, 1, 2, 3, \cdots, n. $ | (9) |
式中:Qk表示k时刻管网中用户用水量,L/s;aQk表示管网中用水量随时间的变化率,L/s2;n表示不同工况的数目.
| $ \begin{array}{*{20}{c}} {{a_{{Q_1}}} = \frac{{{Q_1}-{Q_0}}}{{{t_1}-{t_0}}}, {a_{{Q_2}}} = \frac{{{Q_2}-{Q_1}}}{{{t_2} - {t_1}}}, }\\ {{a_{{Q_3}}} = \frac{{{Q_3} - {Q_2}}}{{{t_3} - {t_2}}}, \cdots, {a_{{Q_k}}} = \frac{{{Q_k} - {Q_{k - 1}}}}{{{t_k} - {t_{k - 1}}}}.} \end{array} $ | (10) |
若aQk为正值,表示管网中用水量增加;若aQk为负值,表示管网中用水量减少.在本研究中,管网系统没有其他控制输入量,即U(k)为零,则供水管网的状态方程为
| $ {X_k} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{X_{k-1}} + \mathit{\boldsymbol{T}}{a_{{{\dot Q}_{k-1}}}} = \left( {\begin{array}{*{20}{c}} 1&{\Delta t}\\ 0&1 \end{array}} \right){X_{k-1}} + \left( {\begin{array}{*{20}{c}} 0\\ {\Delta t} \end{array}} \right){a_{{{\dot Q}_{k - 1}}}}. $ | (11) |
式中:Φ表示供水管网状态转移矩阵;T表示噪声输入矩阵;Δt表示下工况持续运行时间,s;
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \left( {\begin{array}{*{20}{c}} 1&{\Delta t}\\ 0&1 \end{array}} \right), \mathit{\boldsymbol{T}} = \left( {\begin{array}{*{20}{c}} 0\\ {\Delta t} \end{array}} \right), }\\ {{a_{{{\dot Q}_k}}} = \frac{{{a_{{Q_k}}}- {a_{{Q_{k- 1}}}}}}{{{t_k}- {t_{k - 1}}}}, k = 0, 1, 2, 3, \cdots, n, }\\ {E\left( {{a_{{{\dot Q}_k}}}} \right) = 0,E\left[ {{a_{{{\dot Q}_k}}}{{\dot a}_{{Q_j}}}^{\rm{T}}} \right] = Q{\delta _{kj}}.} \end{array} $ | (12) |
式中δkj为Kronecker-δ函数.
综上知
| $ \begin{array}{l} {X_k} = \left( {\begin{array}{*{20}{c}} {{Q_k}}\\ {{a_{{Q_k}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1&{\Delta t}\\ 0&1 \end{array}} \right){X_{k-1}} + \left( {\begin{array}{*{20}{c}} 0\\ {\Delta t} \end{array}} \right){a_{{{\dot Q}_{k-1}}}} = \\ \;\;\;\;\;\;\;\;\left( {\begin{array}{*{20}{c}} 1&{\Delta t}\\ 0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{Q_{k-1}}}\\ {{a_{{Q_{k - 1}}}}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0\\ {\Delta t} \end{array}} \right)\frac{{{a_{{Q_k}}} - {a_{{Q_{k - 1}}}}}}{{{t_k} - {t_{k - 1}}}}, \\ \;\;\;\;\;\;\;\;k = 0, 1, 2, 3, \cdots, n. \end{array} $ | (13) |
供水管网系统的观测信号Zk=(Q1, Q2, Q3, …, Qk),其中Qi(i=1, 2, …, k)表示每一运行工况下的用水总量,计算公式为
| $ {Q_i} = {Q_{zi}}-{\alpha _0}H_i^{{\beta _0}}, i = 1, 2, 3, \cdots, n. $ | (14) |
式中:Qzi表示i工况时的管网总水量(L/s),可在实验中测算出;Hi表示i工况时的管网供水压力(m),可用水泵出口压力、最不利控制点压力和管网中间某节点压力三者的平均值进行计算;α0表示漏损系数;β0表示漏损指数;利用管网供水压力最高值和最低值两组数据,可计算出漏损系数α0和漏损指数β0, 计算公式为
| $ {Q_z} = {Q_k}-{\alpha _0}H_k^{{\beta _0}}, k = 1, 2, 3, \cdots, n. $ | (15) |
式中:Qz表示k时刻管网总水量(L/s), Qk表示k时刻管网总用水量(L/s), Hk表示k时刻管网供水压力(m), α0表示漏损系数, β0表示漏损指数.
则管网系统的观测方程为
| $ \begin{array}{l} {Z_k} = {Q_k} + {V_k} = \mathit{\boldsymbol{H}}{X_k} + {V_k} = \left( {\begin{array}{*{20}{c}} 1&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{Q_k}}\\ {{a_{{Q_k}}}} \end{array}} \right) + {V_k}, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k = 1, 2, 3, \cdots, n. \end{array} $ | (16) |
式中:Zk表示与管网用水量相关的观测值;H表示观测矩阵;Vk表示k时刻的测量噪声,为高斯白噪声,且与
依据上述建立的状态方程和观测方程,利用Kalman滤波算法计算出最终的管网用水量Q′i,管网漏失量由管网总供水量与用户用水量之差求出.状态量的初值X0和误差方差矩阵的初值P0通常难以确定,但是因为该初值对最终滤波分析的结果影响并不显著,且状态量Xk是逐渐收敛的,可将P0取为0,管网中第一个观测值作为初始值X0.
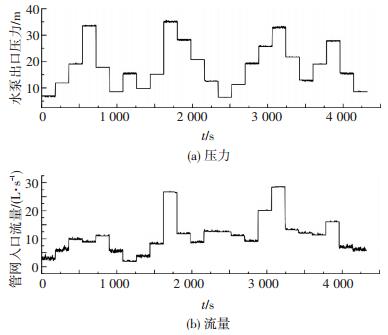
3.3 实验数据分析整理以单水源单漏点环状管网为例,进行24种不同运行工况的模拟,利用SCADA在线数据监测设备记录实验数据(实际应用中也可以使用相同测量方法),实测得到管网中6 426组流量与压力观测信号,并对其进行了预处理,结果如图 3、4所示.
|
图 3 预处理后压力与流量观测信号 Figure 3 Flow and pressure observation signal after pretreatment |

|
图 4 每一工况下压力与流量变化 Figure 4 Flow and pressure change trend chart under each working condition |
从上述数据中分别选取管网供水压力最大值和最小值两组数据,由式(15) 计算出漏损系数α0和漏损指数β0,得α0=0.416 7,β0=0.556 8,可初步计算出每一运行工况下的用水总量Qi,然后在模型中加入系统观测噪声作为观测信号,并采用Kalman滤波算法估算出最终的用水总量Q′i,最后利用差值法求得管网漏失量.将实验中实测的管网漏失量与算法计算出的管网漏失量进行比较,用相对误差表示计算出的管网漏失量偏离实际漏失量的相对大小.一般来说,相对误差更能反映数据的可信程度.计算结果见表 1.
| 表 1 基于Kalman滤波算法计算的漏失量与实验测得漏失量对比 Table 1 Measured water leakage contrast to the estimate with Kalman filter algorithm |
由实验结果可知,基于Kalman滤波分析模型算法模拟计算出的管网漏失量相对于实测的真实漏失量的误差范围为0.12%~9.36%,采用相关系数作为结果可靠性程度的评价指标,相关系数是衡量研究变量之间线性相关程度的量.两个变量越满足线性相关关系,相关系数越接近1.计算得出模拟计算的漏失量与实测的真实漏失量二者的相关系数为0.985,这表明模拟计算的漏失量与实测的漏失量具有非常好的线性相关关系,同时考虑到两者之间的相对误差范围,说明利用Kalman滤波算法模型计算管网系统漏失量是可行且可靠的.
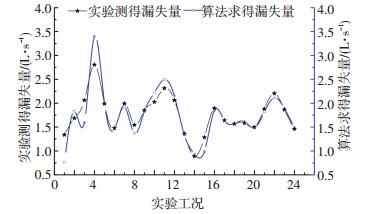
分析图 5可知,在管网系统实验模拟的前几个运行工况中,模拟计算的漏失量与实测漏失量二者的数据拟合程度较差,以前5个工况为例,模拟计算的漏失量与实测的真实漏失量相关系数仅为0.968,原因是在建立数学模型时,将管网中第一个观测信号设定为管网的状态随机变量Xk的初值,但由于Kalman滤波具有实时递推、自我收敛的特性,随着算法的递推进行,状态量会逐渐收敛到最优值,并保持稳定状态.以后10个工况为例,模拟计算的漏失量与实测的真实漏失量相关系数为0.995.这体现了Kalman滤波算法的实时递推性和自回归最优化的特点,也是Kalman滤波算法能够用来计算供水管网漏失量的关键因素.
|
图 5 Kalman滤波算法计算的漏失量与实验测得漏失量对比 Figure 5 Estimate water leakage with Kalman filter algorithm contrast to the measured water leakage |
本研究建立了以Kalman滤波算法为基础的供水管网系统漏失数学模型,充分发挥Kalman滤波算法自身的优势,成功模拟计算出管网漏失量,并采用相对误差和相关系数两个指标来分析模拟计算出的数据和实测数据的吻合程度,结果证明,模拟计算出的数据与实测数据的吻合程度较高.这也证明了利用Kalman滤波算法研究计算管网漏失水量是完全可行可靠的,为下阶段开展降漏工作提供了有力的数据支撑.
| [1] |
董深, 吕谋, 盛泽斌, 等. 基于遗传算法的供水管网反问题流失定位[J].
哈尔滨工业大学学报, 2013, 45(2): 106-128.
DONG S, LU M, SHENG Z B, et al. Inverse transient leakage location of water supply network based on genetic algorithm[J]. Journal of Harbin Institute of Technology, 2013, 45(2): 106-128. DOI: 10.11918/j.issn.0367-6234.2013.02.019 |
| [2] |
伍悦滨, 刘天顺. 基于瞬变反问题分析的给水管网漏失数值模拟[J].
哈尔滨工业大学学报, 2005, 37(11): 1483-1485.
WU Y B, LIU T X. Inverse transient analysis based numerical simulation of leakage in water distribution system[J]. Journal of Harbin Institute of Technology, 2005, 37(11): 1483-1485. DOI: 10.3321/j.issn:0367-6234.2005.11.008 |
| [3] |
GARCÍA V J, CABRERA E. The minimum night flow method revisited[C]// Eighth Annual Water Distribution Systems Analysis Symposium, 2008.DOI:10.1061/40941(247)35.
https://www.researchgate.net/publication/268602124_The_Minimum_Night_Flow_Method_Revisited
|
| [4] |
ALMANDOZ J. Leakage assessment through water distribution network simulation[J].
Journal of Water Resources Planning and Management, 2005, 131(6): 458-466.
DOI: 10.1061/(ASCE)0733-9496(2005)131:6(458) |
| [5] |
李文博. 城市供水管网漏损率量化及控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.
LI W B. Study on quantifying leakage percentage and controlling of urban water supply distributionsystem[D]. Harbin:Harbin Institute of Technology, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10213-1011261703.htm |
| [6] |
高金良, 李娟娟. 区域供水管网盲源分离漏失量研究[J].
哈尔滨工业大学学报, 2015, 47(6): 33-37.
GAO J L, LI J J. Study on leakage of regional distribution network using blind source seperation[J]. Journal of Harbin Institute of Technology, 2015, 47(6): 33-37. DOI: 10.11918/j.issn.0367-6234.2015.06.006 |
| [7] |
KALMAN R E. A new approach to linear filtering and prediction problems[J].
Journal of basic Engineering, 1960, 82(1): 35-45.
DOI: 10.1115/1.3662552 |
| [8] |
KEPPENNE C L. An ensemble recentering Kalman filter with an application to Argo temperature data assimilation into the NASA GEOS-5 coupled model[J].
Ocean Modelling, 2014, 77: 50-55.
DOI: 10.1016/j.ocemod.2014.03.001 |
| [9] |
DI L, KAR S, ALSAADI F E, et al. Distributed Kalman filtering with quantized sensing state, signal processing[J].
IEEE Transactions on, 2015, 63(19): 5180-5193.
DOI: 10.1109/TSP.2015.2450200 |
| [10] |
KULIKOVA M V. Square-root adaptive wave filtering for marine vessels[C]//Control Conference (ECC). European, 2015: 3143-3148
http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7331017
|
 2017, Vol. 49
2017, Vol. 49


