2. 水质科学与水环境恢复工程北京市重点实验室(北京工业大学), 北京 100124
2. Key Laboratory of Beijing for Water Quality Science and Water Environment Recovery Engineering(Beijing University of Technology), Beijing 100124, China
在城市排水系统中,雨水泵站的水泵机组在运行过程中经常会出现频繁启停现象,这一现象往往是由于启泵水位设置不当造成的.若水泵频繁启停,则会对其自身造成严重损害,减少使用寿命[1-3].解决该问题的关键在于如何准确、合理地设置启泵水位,使得机组在运行过程中启停次数最少,将损害降至最低.对此,相关学者做了一定研究.郭磊等[4]采用人工经验调试和水力模型相结合的方法,首先对泵站设计参数进行分析并拟定每个泵的启泵水位,然后运用水力模型进行模拟得到水泵启停次数.反复经历这一调试过程,最终通过比较获得启停次数最少的启泵水位组合,作为水泵机组的最优启泵水位.该方法也是目前较常用的方法,但其人工调试过程较繁琐,同时存在无法确定的人为因素,较难得到理想的启停效果.
暴雨洪水管理模型(storm water management model,SWMM)是一款较为成熟、应用广泛的城市排水系统模拟软件,其对雨水泵站运行的模拟同样得到了广泛应用[5].为解决以上问题,本文通过分析雨水泵站设计参数,建立启泵水位优化模型,并将SWMM模型与优化算法相结合对目标函数进行求解,确定机组的最优启泵水位组合,使得启停次数最少,进而解决水泵频繁启停问题.
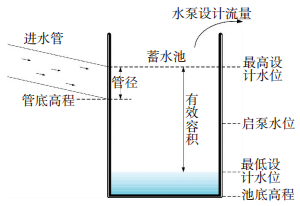
1 启泵水位优化原理设计雨水泵站时需要对蓄水池的有效容积、底面积、最高设计水位和最低设计水位,以及水泵的流量、台数、启泵水位和停泵水位进行设计.《室外排水规范》中规定:蓄水池有效容积依据上游设计流量和下游设计流量进行计算;水泵机组总流量依据下游设计流量而定,水泵宜选用同一型号且数量在2~8台之间;水池的最低设计水位(通常作为停泵水位)根据所选水泵吸水头的要求而定,最高设计水位一般与进水管的管顶相平;有效容积为最高、最低设计水位之间的体积;池底面积依据有效容积和最高、最低设计水位计算;以上设计参数确定后,要设置启泵水位使其满足当水泵机组为自动控制时每小时开泵次数不得超过6次[6].蓄水池设计参数如图 1所示.当遭遇一场降雨事件时,雨水进入管网并汇流至蓄水池上游进水管,通过进水管流入水池.若降雨过程和水池上游管网系统不变,则管网的汇流过程就不变,流入蓄水池的水量也确定不变.因此, 当其他设计参数确定后,对于同一场降雨,影响水泵启停次数的因素仅有启泵水位.
|
图 1 蓄水池设计参数示意 Figure 1 Schematic diagram of storage design parameters |
雨水泵站的水泵数量要在2台以上.在设置每台泵的启泵水位时要按照由低到高合理设置,使得当降雨较小时只有一个泵工作,随着降雨增大,再依次开启其他泵.只有这样设置才可保证水泵启停次数较少.启泵水位设置的过高或过低都会增大启停次数,容易造成频繁启停现象,很难满足规范要求[7-9].最佳启泵水位可利用水力模型经过反复调试来获得.本文选用SWMM模型进行优化研究.SWMM能够模拟降雨、地表径流和管网汇流的过程,其中也包含了通过设置启泵水位来模拟水泵的启停过程.将上游排水管网、下游水池、水泵的设计数据以及当地重现期的设计降雨作为输入,构建SWMM模型,然后在模型中设置启泵水位进行模拟, 并通过模型结果中的水泵流量过程获得启停次数(泵流量从0变为大于0再变回0为一次启停).经过反复调试并对比每次调试的启停次数,即可得到较合适的启泵水位.但此方法的调试过程较繁琐,耗费大量精力.
为避免此问题,可通过构建优化模型来优化启泵水位.雨水泵站通常选取单频泵并联工作,因此, 本文主要针对由单频泵组成的水泵机组进行优化研究.将降雨、管网、水池、水泵等数据输入SWMM中构建SWMM基础模型.在基础模型之上以机组所有水泵的总启停次数为优化目标,以每个水泵的启泵水位为优化变量建立优化目标函数,即
| $ {N_{\min }} = \min F\left( {{h_1},{h_2}, \cdots ,{h_n}} \right). $ | (1) |
式中:Nmin为所有水泵的总启停次数,h1, h2…hn为每台水泵的启泵水位.在SWMM基础模型中设置不同的启泵水位组合便可模拟并获取相应组合的启停次数,进而求解目标函数.
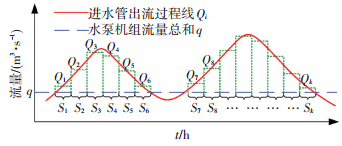
建立目标函数后还需确定自变量h1~hn的约束范围.每台水泵启泵水位的设置均要小于最高限值Hmax,并保证在SWMM模拟计算过程中水池的水位不会超过最高设计水位.同时Hmax也要小于最高设计水位.在机组工作过程中,当池内水位达Hmax时,所有水泵均为开启状态.假设在进水管流量大于各水泵流量总和的这些时间段内,进水管入流体积之和为V1,如图 2、式(2) 和(3) 所示.
|
图 2 流量截取示意 Figure 2 Schematic diagram of flow interception |
| $ {V_1} = \sum\limits_{i = 1}^k {{Q_i} \times {S_i} - q} \times \sum\limits_{i = 1}^k {{S_i}} , $ | (2) |
| $ q = \sum\limits_{i = 1}^n {{q_i}} . $ | (3) |
式中:Si为进水管出流量大于水泵总流量的时段(时段间隔,即SWMM的模拟步长,设置为1 s为宜),Qi为Si时段所对应的进水管出流量,q为所有泵的流量总和,qi为泵i的流量.只要保证Hmax与最高设计水位之间的体积V2不小于V1,即可确保水池的水位不会超过最高设计水位,即
| $ {V_2} = \left( {{H_{\rm{D}}} - {H_{\max }}} \right) \times A \ge {V_1}. $ | (4) |
式中HD为最高设计水位.结合式(2) 和(4) 整理得
| $ {H_{\max }} \le {H_{\rm{D}}} - \left( {\sum\limits_{i = 1}^k {{Q_i} \times {S_i} - q} \times \sum\limits_{i = 1}^k {{S_i}} } \right)/A. $ | (5) |
由式(5) 可以看出,要计算Hmax,就要已知Qi,即要预先获得进水管出流过程线,然而其出流过程线往往是未知的.进水管的出流状态分为自由出流和淹没出流,当水池水位低于进水管管底时为自由出流状态,当高于管底时为淹没出流.在SWMM中可以通过将进水管处的水池替换为出水口并设置出水口为自由出流,来模拟出进水管一直处于自由出流状态的出流过程Qifree,而此状态下的进水管出流量是最大的,既有Qifree≥Qi,进而实现Qi的简化计算.因此可得
| $ \begin{array}{l} {H_{\max }} \le {H_{\rm{D}}} - \left( {\sum\limits_{i = 1}^k {Q_i^{{\rm{free}}} \times {S_i} - q} \times \sum\limits_{i = 1}^k {{S_i}} } \right)/A \le \\ \;\;\;\;\;\;\;\;\;\;{H_{\rm{D}}} - \left( {\sum\limits_{i = 1}^k {{Q_i} \times {S_i} - q} \times \sum\limits_{i = 1}^k {{S_i}} } \right)/A. \end{array} $ | (6) |
最终确定Hmax的计算方法为
| $ {H_{\max }} = {H_{\rm{D}}} - \left( {\sum\limits_{i = 1}^k {Q_i^{{\rm{free}}} \times {S_i} - q} \times \sum\limits_{i = 1}^k {{S_i}} } \right)/A. $ | (7) |
式中:Qifree为SWMM中将水池替换为出水口模拟得到的Si时段对应的进水管出流量.以上Hmax的计算是针对进水管出流峰值大于水泵机组总流量q讨论的,即时段Si是存在的.若q大于出流峰值,则Hmax无限接近HD,保证Hmax < HD即可.此外,启泵水位的最低值要大于停泵水位(即最低设计水位).因此,自变量h1~hn的约束范围
| $ {H_{\min }} < {h_1} \le {h_2} \le \cdots \le {h_n} < {H_{\max }}. $ | (8) |
采用粒子群优化算法对目标函数进行优化计算.粒子群优化算法是较成熟的群体搜索优化算法,并已广泛应用.该算法以粒子为单位,每个粒子具有多维度搜索空间,根据优化问题的评估方法来评价粒子适应度,进行粒子择优.择优后,所有粒子均朝向最优粒子的位置进行速度和位置更新,进而得到下一代群体.如此反复迭代计算,群体逐渐接近最优解,直到满足终止条件为止[10-12].
依据算法原理,在迭代计算之前首先要依据粒子维度,即需要优化的未知变量个数(本文为机组水泵总数),对粒子进行初始化.结合启泵水位优化原理得粒子初始化公式为
| $ h_i^0 = {H_{\min }} + r \times \left( {{H_{\max }} - {H_{\min }}} \right), $ | (9) |
| $ v_i^0 = {v_{\max }} - 2 \times r \times {v_{\max }}. $ | (10) |
式中:hi0为粒子的初始位置,即泵i的启泵水位,Hmax为最高启泵水位,Hmin为最低设计水位,vi0为粒子的初始速度,vmax为粒子速度变化的限值,r为(0, 1) 之间的随机数.群体从初代开始,依据迭代计算过程中得到的历史最优位置和全局最优位置来更新每个粒子的位置和速度[13-16],更新公式为
| $ v_i^{t + 1} = {w^t} \times v_i^t + {c_1} \times r \times \left( {B_i^t - h_i^t} \right) + {c_2} \times r \times \left( {{G^t} - h_i^t} \right), $ | (11) |
| $ h_i^{t + 1} = h_i^t + v_i^t. $ | (12) |
式中:vit为粒子i在第t次迭代中的速度,xit为粒子的位置(启泵水位),c1和c2为学习因子,通常c1=c2=2,r为(0, 1) 之间的随机数,Bit为历史最优位置,Git为全局最优位置,w为惯性系数.本文采用非线性递减策略[17],计算公式如下
| $ {w^t} = {w_{\rm{e}}}{\left( {{w_{\rm{s}}}/{w_{\rm{e}}}} \right)^{1/\left( {1 + {c_{\rm{N}}}t/T} \right)}}. $ | (13) |
式中:ws和we分别为起始和终止时刻惯性系数,通常取ws=0.95和we=0.4,t为当前迭代次数,T为总迭代次数,cN为指数因子,通常取10.本文基于SWMM二次开发技术进行优化计算,步骤如下:
1) 输入降雨、管网、水池和水泵数据,建立SWMM基础模型.
2) 确定最大启泵水位Hmax.将SWMM基础模型中的水池替换为排水口得到改进模型,模拟并得到进水管出流过程线,依据式(7) 计算Hmax.
3) 初始化粒子群体.设置群体规模并根据机组水泵个数确定粒子维度.依据最低设计水位和步骤2) 中获得的Hmax, 结合式(8)、(9) 和(10) 初始化所有粒子的速度和位置,生成初代群体.
4) 计算适应度.将粒子的启泵水位输入到步骤1) 的SWMM基础模型中,调用SWMM计算引擎进行模拟计算.通过读取模型结果计算式(1),得到粒子适应度.
5) 计算历史和全局最优位置.将粒子当前适应度与历史最优解进行比较,得到该粒子的历史最优位置.将所有粒子的历史最优位置进行比较,得到群体的全局最优位置.
6) 更新粒子群体.根据式(13) 计算惯性系数.根据式(11) 和(12) 更新粒子的位置和速度,并判断是否超出约束范围.若超出,则重置到范围内.
7) 判断是否满足终止条件.若满足,则终止计算,返回群体的全局最优位置;若不满足,则返回步骤4).
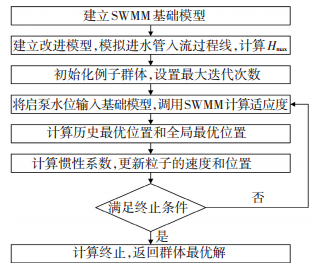
算法的优化流程如图 3所示.
|
图 3 启泵水位优化流程 Figure 3 Optimization procedure of pump start water level |
采用人工调试方法对机组的启泵水位进行人工调试优化.人工调试首先要确定调试参数的合理取值范围,然后对参数进行灵敏度分析,明确参数调整方向及大小.
以某雨水泵站为例,该泵站建有一个调蓄池和一套水泵机组用于减少上游雨水管网的排水压力.水池和水泵机组的设计参数如表 1所示.
| 表 1 水池和水泵设计参数 Table 1 Design parameters of storage and pumps |
首先计算最高启泵水位Hmax.当地设计重现期为10年一遇,因此依据以上设计参数和当地10年一遇的24 h设计降雨过程线,建立SWMM模型.设置模拟步长为1 s并模拟进水管为自由出流状态下的出流过程线,如图 4所示.

|
图 4 进水管流量过程线 Figure 4 Flow curve of water inlet |
图 4中进水管出流量Qifree大于水泵机组总设计流量的时段为16:59:36—17:10:34,根据式(7) 计算Hmax为4.84 m,并依据最低设计水位Hmin=1 m确定启泵水位取值范围为1 m < h1≤h2≤h3≤h4 < 4.84 m.
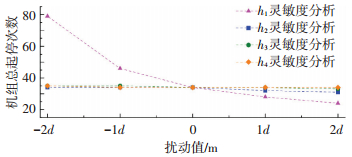
采用扰动法对启泵水位进行灵敏度分析.将4台泵的启泵水位在Hmin和Hmax之间按照由低到高等间距分布,作为启泵水位的4个基准值.在某一基准值附近给定扰动值(本实例采用泵之间的间距除以3,记为d,将基准值-2d、-d、+d、+2d作为扰动值),而保持其他启泵水位不变,计算水泵机组总启停次数.灵敏度分析结果如图 5所示.
|
图 5 启泵水位灵敏度分析 Figure 5 Sensitivity analysis of pump start level |
以启泵水位为横坐标,机组总启停次数为纵坐标,进行线性回归曲线拟合,各泵的启泵水位拟合曲线斜率如表 2所示.斜率的大小反应了参数的灵敏度,斜率的正负反应了总启停次数变化方向.根据斜率值可以看出h1~h4的灵敏度逐渐减小,因此, 在人工调试时应按照h1~h4的顺序进行调试.以启泵水位的基准值为初始值进行人工调试,其调试过程如表 3所示.
| 表 2 启泵水位变化值的拟合斜率 Table 2 Fitting slope of pump level changing |
| 表 3 启泵水位的人工调试过程 Table 3 Artificial debugging process of pump level |
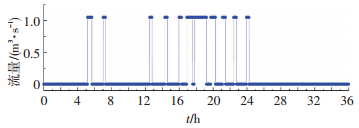
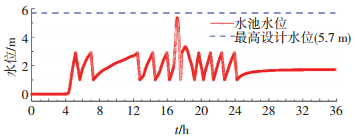
经过人工调试获得最优启泵水位如表 3中的调试3.其中泵1~泵4的启停次数分别为11次、1次、1次、1次.检验优化结果是否合理不仅要保证机组总启停次数最少,还要将得到的启泵水位输入SWMM中模拟,保证满足《室外排水规范》中提出的单个泵每小时启停次数不超过6次以及水池的水位要始终低于最高设计水位.在4台泵中只有泵1的启停次数累计超过6次,因此, 将人工调试结果输入SWMM中模拟(考虑到管网汇流的滞后性,设置总模拟时长为36 h),并获得泵1的流量过程和水池的水位过程如图 6和7所示.从图 6和7可以看出, 泵1每小时启停次数均在6次以内,水池的水位低于最高设计水位,满足要求.可见,采用人工调试的方法将启泵水位在合理的范围内进行调整可以使启停次数逐渐减少并最终得到一个较为理想的启泵水位组合.
|
图 6 人工调试结果中泵1流量过程线 Figure 6 Flow curve of pump 1 in artificial debugging result |
|
图 7 人工调试结果中水池水位过程线 Figure 7 Water level curve of storage in artificial debugging result |
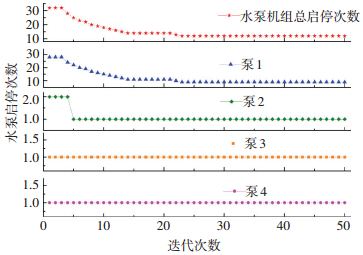
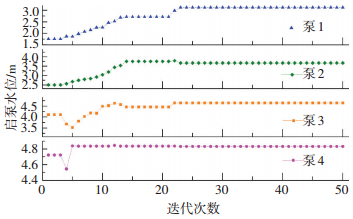
运用本文优化算法对启泵水位进行优化.各项设计参数、最高启泵水位Hmax等输入条件与实例一相同.设置粒子群体规模为20,优化迭代次数为50次.粒子速度的约束条件见式(14),根据式(9) 和(10) 始化粒子群体.进行迭代计算,得到水泵启停次数和启泵水位的优化计算过程如图 8和9所示.
| $ \left\{ \begin{array}{l} \left| {{v_1}} \right| \le {h_2} - {H_{\min }},\\ \left| {{v_i}} \right| \le {h_{i + 1}} - {h_{i - 1}},\left( {i = 2,3} \right)\\ \left| {{v_4}} \right| < {H_{\max }} - {h_3}. \end{array} \right. $ | (14) |
|
图 8 水泵启停次数优化过程 Figure 8 Optimization procedure of pump start-stop times |
|
图 9 启泵水位优化过程 Figure 9 Optimization procedure of pump start level |
由图 8可以看出, 随着迭代次数增加,粒子适应度(水泵机组总启停次数)不断减小,在第23次迭代之后达到稳定.由图 9可以看出,泵1和泵2的启泵水位不断趋近于最优解,而泵3和泵4的启泵水位在一定的波动之后达到稳定值.最终得到最优启泵水位如表 4所示.
| 表 4 水泵机组运行参数优化结果 Table 4 Optimization result of pump operating parameters |
由表 4可看出,只有泵1启停次数累计超过6次.与实例一相同,将最优启泵水位输入SWMM进行模拟来验证泵1每小时内的启停次数和水池水位变化.泵1的流量过程线和水池的水位过程线如图 10和11.

|
图 10 泵1流量过程线 Figure 10 Flow curve of pump 1 |

|
图 11 水池水位过程线 Figure 11 Water level curve of storage |
由图 10可以看出,泵1每小时的启停次数均小于6次,图 11中水池的水位最高达到5.54 m,小于最高设计水位5.7 m.因此,运用优化算法得到的启泵水位满足要求,可以作为该泵站的启泵水位进行设置.
对比实例一和实例二的优化过程,采用优化算法进行优化计算,无需工作人员有较多的调试经验即可获得较为合适的启泵水位,并且在优化过程中避免了较多工作量的投入和对参数影响进行大量分析.
4 结论1) 雨水泵站的启泵水位如果设置不合理,会造成水泵启停频繁.通过人工调试的方法运用水力模型对启泵水位进行反复调试,能够获得最佳启泵水位使得水泵启停次数满足规范要求.
2) 本文提出一种将优化算法与水力模型相结合的方法来优化启泵水位.该方法通过构建启泵水位优化模型,用SWMM对目标函数求解,进而得到最佳启泵水位并使得启停次数最少且满足规范要求.优化得到的启泵水位可以应用于雨水泵站,通过实例对此进行了验证.
3) 与人工调试方法相比,本文方法可以通过计算机自行优化计算,无需复杂的人工调试过程并且能够获得较好的启停效果,可以指导启泵水位的选取.
| [1] |
张建新, 吕锐, 贺田富. 下穿式道路立交雨水泵站排水设计参数探讨[J].
给水排水, 2012, 38(1): 30-35.
ZHANG Jianxin, LV Rui, HE Tianfu. Probe into design parameters of undercrossing grade separation drainage system for rainwater pump station[J]. Water & Wastewater Engineering, 2012, 38(1): 30-35. DOI: 10.13789/j.cnki.wwe1964.2012.01.019 |
| [2] |
刘澜, 王峰, 李杨秋, 等. 厦门机场路雨水泵站调蓄优化设计[J].
给水排水, 2009, 35(5): 50-52.
LIU Lan, WANG Feng, LI Yangqiu, et al. Optimization design of water pump station in Xiamen Airport Road[J]. Water & Wastewater Engineering, 2009, 35(5): 50-52. |
| [3] |
孙艳涛. 下穿铁路立交桥排水泵站设计及安全防护[J].
给水排水, 2015, 41(4): 45-47.
SUN Yantao. Design and safety protection of drainage pumping station under interchange[J]. Water & Wastewater Engineering, 2015, 41(4): 45-47. DOI: 10.13789/j.cnki.wwe1964.2015.0123 |
| [4] |
郭磊, 姚双龙, 李玢, 等. 基于水力模型的下凹式立交桥桥区雨水泵站运行优化[J].
给水排水, 2014, 40(3): 102-104.
GUO Lei, YAO Shuanglong, LI Bin, et al. Concave-down overpass rainwater pump station operation optimization based on hydraulic model[J]. Water & Wastewater Engineering, 2014, 40(3): 102-104. DOI: 10.13789/j.cnki.wwe1964.2014.0025 |
| [5] |
王彤, 刘志强, 李晓娜, 等. 城市雨水泵站运行效果模拟及优化调控分析[J].
水电能源科学, 2016, 34(3): 181-184.
WANG Tong, LIU Zhiqiang, LI Xiaona, et al. Simulation and optimization analysis of urban storm water pump station operation[J]. Water Resources and Power, 2016, 34(3): 181-184. |
| [6] |
中华人民共和国建设部. 室外排水设计规范: GB 50014—2006[S]. 北京: 中国计划出版社, 2014: 45-50.
Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for design outdoor wastewater engineering: GB 50014—2006[S]. Beijing: China Planning Press, 2014: 45-50. |
| [7] |
俞锋. 城镇排水泵站集水池设计水位的确定[J].
浙江建筑, 2011, 28(6): 54-56.
YU Feng. Determination of the collection basin design water level of drainage pumping station[J]. Zhejiang Construction, 2011, 28(6): 54-56. DOI: 10.15874/j.cnki.cn33-1102/tu.2011.06.016 |
| [8] |
刘猛, 陶月赞, 郭增辉. 下穿既有铁路线立交桥雨水泵站设计[J].
工程建设与设计, 2011(3): 111-114.
LIU Meng, TAO Yuezan, GUO Zenghui. Design of overpass rainwater pump station in crossing existing railway[J]. Construction & Design for Project, 2011(3): 111-114. |
| [9] |
刘欣. 城市排水泵站的优化运行管理[D]. 天津: 天津大学环境学院, 2011: 21-36.
LIU Xin. Optimization of operation and regulation of urban drainage pump station[D]. Tianjin: TianjinUniversity, College of the Environment, 2011: 21-36. http://cdmd.cnki.com.cn/Article/CDMD-10056-1012008165.htm |
| [10] |
LI Yuhua, ZHAN Zhihui, LIN Shujin, et al. Competitive and cooperative particle swarm optimization with information sharing mechanism for global optimization problems[J].
Information Sciences, 2015, 293: 370-382.
DOI: 10.1016/j.ins.2014.09.030 |
| [11] |
ASHTIANI E F, NIKSOKHAN M H, ARDESTANI M. Multi-objective waste load allocation in river system by MOPSO algorithm[J].
International Journal of Environmental Research, 2015, 9(1): 69-76.
|
| [12] |
GHOSHAL S P. Optimizations of PID gains by particle swarm optimizations in fuzzy based automatic generation control[J].
Electric Power Systems Research, 2004, 72(3): 203-212.
DOI: 10.1016/j.epsr.2004.04.004 |
| [13] |
MENDONCA I M, SILVA I C, MARCATO A L M. Static planning of the expansion of electrical energy transmission systems using particle swarm optimization[J].
International Journal of Electrical Power & Energy Systems, 2014, 60: 234-244.
|
| [14] |
JIANG Yan, LI Xuyong, HUANG Chongchao. Automatic calibration a hydrological model using a master-slave swarms shuffling evolution algorithm based on self-adaptive particle swarm optimization[J].
Expert Systems with Applications, 2013, 40(2): 752-757.
DOI: 10.1016/j.eswa.2012.08.006 |
| [15] |
YANG Wen'an, ZHOU Wei, LIAO Wenhe, et al. Prediction of drill flank wear using ensemble of co-evolutionary particle swarm optimization based-selective neural network ensembles[J].
Journal of Intelligent Manufacturing, 2016, 27(2): 343-361.
DOI: 10.1007/s10845-013-0867-2 |
| [16] |
JIANG Yan, LIU Changmin, HUANG Chongchao, et al. Improved particle swarm algorithm for hydrological parameter optimization[J].
Applied Mathematics and Computation, 2010, 217(7): 3207-3215.
DOI: 10.1016/j.amc.2010.08.053 |
| [17] |
SHI Y, EBERHART R. Empirical study of particle swarm optimization[C] // Proceeding of the 1999 Congress on Evolutionary Computation. Washington: IEEE, 1999: 1945-1950
|
 2017, Vol. 49
2017, Vol. 49


