市政有限空间不同于地面设施,其长期处于封闭或半封闭状态,自然通风不良,在热膨胀、重气积聚等物理作用,金属腐蚀、物质氧化等化学反应,以及微生物耗氧等的作用下,极易出现氧气缺乏、有毒有害气体积聚等问题,对其内部作业人员的安全构成了严重威胁[1-3].国外较早关注有限空间作业安全问题.文献[4-5]的研究表明,在有限空间致死原因中,中毒和窒息占62%,远高于淹溺、坠落等其它致死因素.美国职业安全与卫生研究所(NIOSH)在有限空间事故方面做了大量研究工作,出版了一系列研究成果[6-8],对有限空间事故预防起了积极作用.近年来,中国也高度重视有限空间作业安全,文献[9-12]也从有限空间危害因素辨识、事故预防控制措施及监督管理方面开展了研究工作.
为保证作业人员的安全,国家安监总局在2013年发布《工贸企业有限空间作业安全管理与监督暂行规定》,提出有限空间作业应严格遵守“先通风、再检测、后作业”的原则,在2014年发布的《有限空间安全作业五条规定》中,再次强调有限空间作业必须“先通风、再检测、后作业”,严禁通风、检测不合格的情况下进行作业.因此,在进入有限空间作业前进行强制通风是保障作业人员安全的必不可少的重要步骤.目前,在供热有限空间的通风过程中,通风方式、通风时间等都是根据经验确定,缺少理论依据,不仅影响工作效率,也不能充分保障作业人员的安全.本文采用计算机数值模拟的方法,对供热有限空间强制通风过程进行数值模拟,得出不同通风状态下小室内温度、氧气体积分数、二氧化碳体积分数的恢复规律,从而为作业前强制通风提供理论依据和技术支撑.
1 数值模拟基本方程供热有限空间在通风换气过程中,最大风速远小于声速340 m·s-1,因此,空气可以看作不可压缩流体.通风过程是无化学反应的非稳态单相多组分扩散问题,计算流体动力学中,主要根据质量守恒、动量守恒、能量守恒和组分传输守恒4项定律,建立用于描述多组分三维非定常湍流流动的控制方程组[13-15].
1) 质量守恒方程(也称连续性方程)
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}} \right) = 0. $ |
2) 动量方程
| $ \frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}} + \rho {g_i} + {F_i}. $ |
3) 能量方程
| $ \begin{array}{c} \frac{\partial }{{\partial t}}\left( {\rho E} \right) + \frac{\partial }{{\partial {x_i}}}\left[ {{u_i}\left( {\rho E + p} \right)} \right] = \\ \frac{\partial }{{\partial {x_i}}}\left( {{k_{{\rm{eff}}}}\frac{{\partial T}}{{\partial {x_i}}} - \sum {{J_c}} \int_{{T_{{\rm{ref}}}}}^T {{c_{{\rm{pc}}}}{\rm{d}}T} + {u_i}{{\left( {{\tau _{ij}}} \right)}_{{\rm{eff}}}}} \right) + {S_{\rm{h}}}.\\ E = \sum {{\omega _{\rm{c}}}} \int_{{T_{{\rm{ref}}}}}^T {{c_{{\rm{pc}}}}{\rm{d}}T} + \frac{{{v^2}}}{2}. \end{array} $ |
4) 组分传输守恒方程
| $ \frac{\partial }{{\partial t}}\left( {\rho {\omega _{\rm{c}}}} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}{\omega _{\rm{c}}}} \right) = \frac{\partial }{{\partial {x_i}}}\left( {\rho {D_{\rm{c}}}\frac{{\partial {\omega _{\rm{c}}}}}{{\partial {x_i}}}} \right). $ |
5)k-ε湍流方程
k方程
| $ \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}k} \right) = \frac{\partial }{{\partial {x_i}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _{\rm{k}}}}}} \right)\frac{{\partial k}}{{\partial {x_i}}}} \right] + {G_{\rm{k}}} - \rho \varepsilon . $ |
ε方程
| $ \begin{array}{c} \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}\varepsilon } \right) = \frac{\partial }{{\partial {x_i}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial k}}{{\partial {x_i}}}} \right] + \frac{{{C_{\varepsilon 1}}}}{k}{G_{\rm{k}}} - {C_{\varepsilon 2}}\rho \frac{{{\varepsilon ^2}}}{k}.\\ {\mu _{\rm{t}}} = {C_{\rm{ \mathsf{ μ} }}}\rho \frac{{{k^2}}}{\varepsilon },{G_{\rm{k}}} = {\mu _{\rm{t}}}\frac{{\partial {u_j}}}{{\partial {x_i}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right). \end{array} $ |
式中:ρ为气体密度,kg·m-3;v为流体速度,m·s-1;ui为流体在x、y、z方向上的速度,m·s-1;xi为x、y、z方向上的坐标,m;p为流体压力,Pa;τij为应力张量,N·m-2;gi为i方向上的重力体积力,N·kg-1;Fi为i方向上外部体积力,N;E为流体能量,J;keff为有效导热率;Jc为组分c的扩散通量;Sh为体积热源;ωc为组分c的质量分数;Dc为组分c的扩散系数;cpc为组分c的比热容,J·(kg·K)-1;k为湍动能,m2·s-2;ε为湍动能耗散率,m2·s-3;Gk为湍动能变化率; μ为层流黏性系数; μt为湍流黏性系数,Pa·s;Cε1、Cε2、Cμ、σε、σk、Tref为常数,分别取1.44、1.92、0.09、1.3、1.0、298.15 K.
2 数值模拟模型建立 2.1 几何模型的建立选取现场调研中某供热有限空间为研究对象.供热小室长6 m,宽5 m,高6 m,小室顶部距地面(即井筒深)4 m,两个入口井在小室对角,且井口下方有金属平台和金属阶梯.在小室两侧分别有宽3 m,高2.5 m的拱形管沟,管沟内距小室100 m处设有直径0.7 m的通风井.两根直径0.8 m(包括保温层)的供热管道沿着管沟走向布置,供热管道在小室内分支出两条直径0.6 m的管道从小室侧面穿出,在接口处设有阀门.由于平台和阶梯的扶栏以及管道的阀门结构较小,对小室内流场分布的影响也较小,从简化模型降低计算量的角度考虑,在此忽略不计.根据现场实际,采用GAMBIT建立三维几何模型(如图 1所示).采用三维Tet /Hybrid网格单元、TGrid网格类型对模型进行网格划分,网格基本尺寸为0.2 m,网格总数为240 611个.
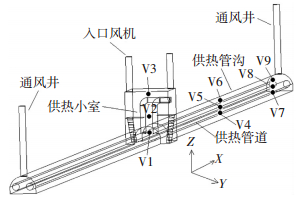
|
图 1 供热管沟几何模型 Figure 1 Geometric model of heating pipe tunnel |
几何模型原点(0, 0, 0) 设在供热小室底部中心,沿管沟走向为X轴,垂直管沟走向的水平方向为Y轴,竖直向上为Z轴.为观测通风过程中关键点的参数值,共设置9个观测点,坐标分别为V1(0, 0, 1)、V2(0, 0, 3)、V3(0, 0, 5.9)、V4(50, 0, 0.5)、V5(50, 0, 1)、V6(50, 0, 1.9)、V7(99, 0, 0.5)、V8(99, 0, 1)、V9(99, 0, 1.9).
2.2 模拟参数的设置及求解边界条件设置中,通风风量分别设置为6 000、8 000、10 000、12 000、14 000 m3·h-1,并根据入口大小,转换为速度入口,相应入口风速分别为4.33、5.77、7.22、8.66、10.1 m·s-1.出口设为自由流出,供热管道表面设为热源壁面,温度为60 ℃恒温.小室内原始气体成分体积分数和内部温度,以及其他数值模拟参数根据现场实际调研结果设置,如表 1所示[16-17].
| 表 1 数值模拟参数设置 Table 1 Simulation parameters settings |
将划分好网格的几何模型导入到Fluent软件,按照表 1设置好相应参数,采用32核工作站进行并行计算.计算结果中连续性残差值、速度残差值、能量残差值、k残差值、ε残差值及气体各组分残差值均<0.001,计算结果满足收敛性要求.
3 数值模拟结果及分析 3.1 流场分布规律通风换气过程中,流场分布情况直接影响通风换气的效果.在通风初期,管沟内气体从几乎静止开始流动,气体的原始状态对风流场的影响较大,为避免这一影响,选取通风10 min后的流场进行分析(根据模拟结果,10 min时管沟内流场已不再受流场原始状态的影响).在此以通风量6 000 m3·h-1为例,风流速度矢量图和X截面风速云图如图 2、3所示.
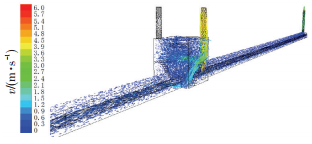
|
图 2 管沟内风流速度矢量图 Figure 2 Velocity vector of airflow in tunnel |
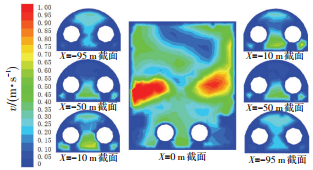
|
图 3 沿管沟走向不同横截面风速分布云图 Figure 3 Airflow velocity contours of different cross sections along the pipe tunnel |
由图 2、3可以看出:1) 新鲜风流从井口送入后,以较大速度竖直向下注入小室,在小室内部由于受到平台的阻碍作用,风流向小室中央扩散.风流在小室内形成了较大涡流,且风速分布极不均匀,小室中部风速较大,达1 m·s-1以上,而在小室的顶部和底部供热管道两侧风速较小,仅为0.1 m·s-1.2) 风流从小室进入管沟,方向发生急剧偏转,在管沟顶部形成涡流,因此,在距小室10 m以内的管沟顶部出现部分气流逆流现象.3) 在10 m以后管沟内风流较为稳定,风流主要是沿管沟底部流向两侧通风井,管沟顶部区域风速较小,不足0.1 m·s-1.根据对温度场的分析可知,热空气上升在顶部积聚,造成了管沟底部风流速度大,顶部速度小.4) 风流速度场的分布直接影响着氧气体积分数的恢复速率,因此,在研究氧气体积分数变化时应重点关注小室顶部和底部角落、管沟顶部的氧气体积分数.
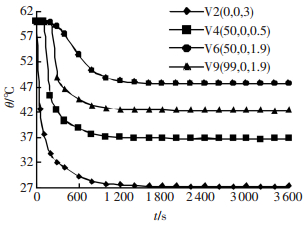
3.2 温度场分布规律供热管道内热水或热气温度高达140 ℃以上,在采取保温隔热措施后,仍有部分热量散入管沟空间,保温层表面温度为60 ℃左右.以通风风量6 000 m3·h-1为例,通风10 min后管沟和小室不同截面温度分布云图如图 4所示,通风过程中不同观测点温度变化如图 5所示.
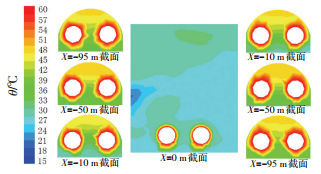
|
图 4 沿管沟走向不同横断面温度分布云图 Figure 4 Temperature contours of different sections along the pipe tunnel |
|
图 5 观测点温度随通风时间变化曲线 Figure 5 Temperature of different observation points as a function of time |
由图 4、5可知:1) 通风过程中小室内温度降低较快,小室内温度场分布呈现中间低、顶部和底部高的趋势.主要是由于小室顶部存在局部湍流区域,风速较小,温度降低较慢;而在小室底部供热管道不断散发热量,因此,管道周围温度较高,但高温区域相对较小.2) 管沟内温度场分布呈现明显的顶部高、底部低的趋势,即供热管道以上区域温度高,供热管道以下区域温度低,上下温差约为11 ℃,供热管道周围高温区域范围较大.主要是由于在热升力的作用下,热空气上浮,在顶部集聚,此外温度场的分布也影响了风流场的分布,管沟底部风流速度大于顶部,也进一步加剧了温度场的分布不均.3) 通风量为6 000 m3·h-1时,通风25 min后各观测点的温度均降低至一稳定值,此后空间内温度场达到稳定状态,温度稳定时观测点中管沟中段顶部点(50,0,1.9) 的温度最高,约为49 ℃,小室内温度较低,观测点(0,0,3) 温度约为27 ℃.
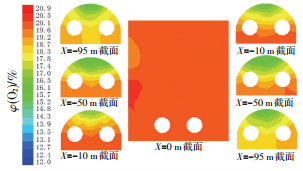
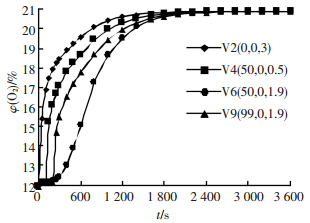
3.3 氧气体积分数分布规律以风机风量6 000 m3·h-1为例,通风10 min时,管沟和小室不同截面氧气体积分数分布如图 6所示.沿管沟走向,不同高度氧气体积分数沿程分布如图 7所示.通风过程中不同观测点处的氧气体积分数恢复曲线如图 8所示.
|
图 6 不同截面氧气体积分数分布云图 Figure 6 Oxygen content contours of different cross sections along the tunnel |

|
图 7 管沟内氧气体积分数沿程变化曲线 Figure 7 Oxygen content curves along x-direction line at different height from the tunnel floor |
|
图 8 不同观测点氧气体积分数恢复曲线 Figure 8 Oxygen content histories of different observation points as a function of time |
由6~8可以看出:1) 在通风过程中氧气体积分数分布与风速分布基本一致,在小室内氧气体积分数恢复较快且分布均匀,在管沟内氧气体积分数呈明显底部高顶部低的分层现象.2) 沿着管沟走向,z=0.5 m高度氧气体积分数呈现逐渐线性减小,随着离底面高度增加,氧气体积分数呈现先减小后增大的趋势,特别是z=1.9 m高度的沿线,在距小室65 m处,氧气体积分数最低,为15.2%.氧气体积分数的沿程分布说明,管沟内原始热空气的热升力影响了风流场的分布,进而影响了氧气体积分数的恢复.3) 各观测点的氧气体积分数开始恢复较快,随后上升速率逐渐减缓,直至氧气体积分数恢复至20.9%.其中小室内观测点(0, 0, 5.9) 处氧气体积分数在10 min时达到19.5%(低于该值即为缺氧),40 min时恢复到正常值20.9%;管沟中部观测点(50, 0, 1.9) 处氧气体积分数恢复最慢,20 min时达19.5%,40 min时恢复到正常值20.9%.可以看出小室和管沟内氧气体积分数恢复速率不同,但氧气体积分数恢复至正常值的时间基本一致.
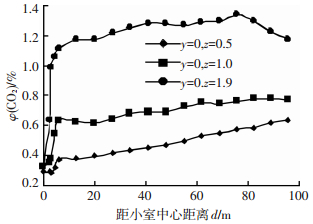
3.4 二氧化碳体积分数分布规律以风机风量6 000 m3·h-1为例,通风10 min时,管沟和小室不同截面二氧化碳体积分数分布如图 9所示,沿管沟走向,不同高度二氧化碳体积分数沿程分布如图 10所示,不同观测点处的二氧化碳体积分数恢复曲线如图 11所示.

|
图 9 不同截面二氧化碳分布云图 Figure 9 Carbon dioxide content contours of different cross sections along the tunnel |
|
图 10 管沟内二氧化碳体积分数沿程变化曲线 Figure 10 Carbon dioxide content curves along x-direction line at different height from the tunnel floor |

|
图 11 不同观测点二氧化碳体积分数恢复曲线 Figure 11 Carbon dioxide content histories of different observation points as a function of time |
由图 9~11可以看出:1) 通风过程中二氧化碳体积分数分布与氧气体积分数分布正好相反,沿着管沟走向,二氧化碳体积分数呈现底部低顶部高的分布规律.2) 沿着管沟走向,离底面0.5 m高度二氧化碳体积分数呈现逐渐线性增大,随着离底面高度的增加,二氧化碳体积分数沿程呈现明显的先增大后减小的趋势.3) 小室和管沟内各观测点的二氧化碳体积分数降低速率不同,但各点二氧化碳体积分数恢复到正常值的时间基本一致,且与氧气体积分数恢复到正常值相同.
3.5 风机风量对换气效果的影响为研究不同的风量下供热有限空间内温度、氧气体积分数、二氧化碳体积分数随时间的变化,分别模拟风量为6 000、8 000、10 000、12 000、14 000 m3·h-1时的通风过程.根据前文分析,选取管沟内温度降低较慢、氧气体积分数和二氧化碳体积分数恢复较慢的观测点V6(50, 0, 1.9) 为分析点,其温度、氧气体积分数、二氧化碳体积分数随时间变化曲线如图 12~14所示.
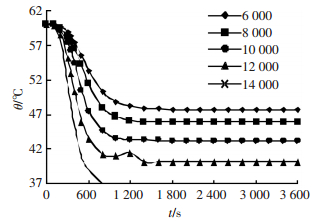
|
图 12 不同通风量下温度恢复曲线 Figure 12 Temperature histories of different ventilation flow rate as a function of time |
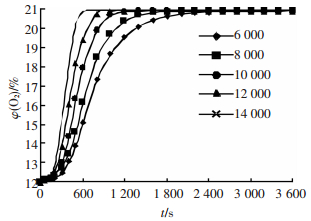
|
图 13 不同通风量下氧气体积分数恢复曲线 Figure 13 Oxygen content histories of different ventilation flow rate as a function of time |
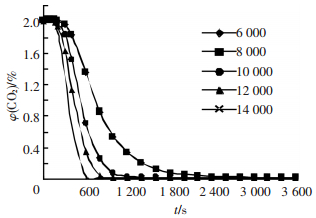
|
图 14 不同通风量下二氧化碳体积分数恢复曲线 Figure 14 Carbon dioxide content histories of different ventilation flow rate as a function of time |
由图 12~14可以看出:1) 随着通风风量的加大,管沟内温度降低越快,且达到稳定状态时的温度也越低.对于该供热有限空间,通风量为6000、8 000、1 0000、12 000、14 000 m3·h-1时,温度降到稳定状态的时间分别为25、18、15、12、10 min,稳定时的温度为48、46、43、40、37 ℃.2) 氧气体积分数的增加和二氧化碳体积分数的降低随时间变化基本一致,即在通风过程中空间内低体积分数气体回升和高体积分数气体下降均在相同的时间内恢复到正常值.对于该供热有限空间,所模拟的几种风量下气体成分体积分数恢复到正常值的时间分别为45、32、22、15、10 min.3) 从通风过程中温度场降到稳定, 氧气体积分数、二氧化碳体积分数恢复到正常值所需的时间,及稳定时内部温度等方面考虑,该供热有限空间通风换气风量为6 000、8 000、10 000、12 000、14 000 m3·h-1时,通风时间应分别不小于45、32、22、15、10 min.
4 模拟结果验证为了验证模拟结果的正确性,进行了现场实际通风测试.轴流风机风量为12 000 m3·h-1,选用英思科GasBadge Pro氧气检测记录仪记录通风过程中氧气体积分数,通风前测试人员佩戴正压式空气呼吸器进入管沟,将检测仪固定在管沟中段顶部位置.通风30 min后进入取出,检测结果如图 15所示.可以看出,数值模拟结果与实测值基本一致.数值模拟中氧气体积分数初始值按照第一次检测结果设置为12.0%,而通风试验时所测为12.6%,因此,在通风过程前6 min数值模拟结果小于实测值;之后数值模拟结果大于实测值,且数值模拟比实际先恢复到正常值.主要是由于试验中风机与井口存在漏风,有效通风量小于12 000 m3·h-1,因此,在实际通风过程中应尽量保证风机与井口间的严密性.
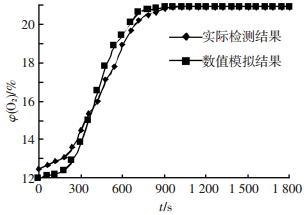
|
图 15 数值模拟结果与实测结果对比 Figure 15 Comparison of oxygen concentration between simulated model and field measurement |
1) 数值模拟方法能够全面、直观地反映通风换气过程,评估通风换气效果,结果可为实际作业提供理论参考和技术支撑.
2) 供热有限空间通风换气过程中,内部风流场的分布不仅受内部结构影响,还受温度场的影响,在两种因素的共同作用下,管沟内风流主要沿着管沟底部流动,而管沟顶部风流相对较小.
3) 通风过程中内部温度场的分布一方面影响着风流场的分布,另一方面受风流场分布的影响,在二者的相互作用下,管沟内温度呈现底部低、顶部高的分布规律.
4) 通风过程中氧气和二氧化碳体积分数恢复随时间变化较为一致,二者恢复至正常值所需时间相同,在实际通风过程中可仅以氧气体积分数恢复情况作为衡量通风效果的代表气体.管沟中段顶部气体成分体积分数恢复较慢,通风过程中宜将该区域的气体成分体积分数值作为衡量通风效果的关键参数.
5) 针对所研究的供热有限空间,通风换气风量为6 000、8 000、10 000、12 000、14 000 m3·h-1时,通风时间应分别不小于45、32、22、15、10 min,实际作业中还应乘以合适的安全系数.
| [1] |
MCMANUS N.
Safety and health in confined spaces[M]. Florida: CRC Press, 1998.
|
| [2] |
王山, 傅贵, 秦妍, 等. 有限空间作业事故原因及预防方法研究[J].
工业安全与环保, 2012, 38(10): 57-59.
WANG Shan, FU Gui, QIN Yan, et al. Study on causes and preventions for confined space accidents[J]. Industrial Safety and Environmental Protection, 2012, 38(10): 57-59. DOI: 10.3969/j.issn.1001-425X.2012.10.019 |
| [3] |
BURLET-VIENNEY D, CHINNIAH Y, BAHLOUL A, et al. Occupational safety during interventions in confined spaces[J].
Safety Science, 2015, 79: 19-28.
DOI: 10.1016/j.ssci.2015.05.003 |
| [4] |
SURUDA A J, PETTIT T A, NOONAN G P, et al. Deadly rescue: The confined space hazard[J].
Journal of Hazardous Materials, 1994, 36(1): 45-53.
DOI: 10.1016/0304-3894(93)E0051-3 |
| [5] |
WILSON M P, MADISON H N, HEALY S B. Confined space emergency response: assessing employer and fire department practices[J].
Journal of Occupational & Environmental Hygiene, 2012, 9(2): 120-128.
|
| [6] |
National Institute for Occupational Safety and Health.
Criteria for A recommended standard: Working in confined spaces[M]. Morgantown: DHHS (NIOSH) Publication, 1979: 80-106.
|
| [7] |
National Institute for Occupational Safety and Health.
Request for assistance in preventing occupational fatalities in confined spaces[M]. Morgantown: DHHS (NIOSH) Publication, 1986: 86-110.
|
| [8] |
National Institute for Occupational Safety and Health.
A guide to safety in confined spaces[M]. Morgantown: DHHS (NIOSH) Publication, 1987: 87-113.
|
| [9] |
高建明, 魏利军. 有限空间的危害辨识与风险控制研究[J].
工业安全与环保, 2005, 31(6): 53-54.
GAO Jianming, WEI Lijun. Studies on hazards identification and risk control of confined space[J]. Industrial Safety and Environmental Protection, 2005, 31(6): 53-54. |
| [10] |
宋元宁, 张庆明, 冯冰. 有限空间气体危害案例及安全对策[J].
安全, 2007, 28(11): 34-35.
SONG Yuanning, ZHANG Qingming, FENG Bing. Gas hazard cases and safety countermeasures in confined space[J]. Safety, 2007, 28(11): 34-35. DOI: 10.3969/j.issn.1673-887X.2007.11.020 |
| [11] |
杨宏刚, 赵江平, 张璇. 有限空间作业危害辨识及事故控制[J].
建筑安全, 2013(2): 63-67.
YANG Honggang, ZHAO Jiangping, ZHANG Xuan. Hazard identification and accident control in confined space[J]. Construction Safety, 2013(2): 63-67. |
| [12] |
王丽华, 王莉萍, 乔丽娟, 等. 由氩气窒息事故看密闭空间作业的防护对策[J].
环境与职业医学, 2007, 24(3): 291-292.
WANG Lihua, WANG Liping, QIAO Lijuan. The protection measure for enclosed space work in the light of an argon gas suffocation accident[J]. Journal of Environmental and Occupational Medicine, 2007, 24(3): 291-292. |
| [13] |
GIANNISSIS G, SHENTSOV V, MELIDEO D, et al. CFD benchmark on hydrogen release and dispersion in confined, naturally ventilated space with one vent[J].
International Journal of Hydrogen Energy, 2015, 40(5): 2415-2429.
DOI: 10.1016/j.ijhydene.2014.12.013 |
| [14] |
ZHAO J, MANBECK H B, MURPHY D J. Computational fluid dynamics simulations of gas evacuation and O2 recovery times for fan-ventilated confined-space manure pits[J].
Studies in Foreign Education, 2008, 51(6): 2135-2149.
|
| [15] |
WIDIATMOJO A, SASAKI K, WIDODO N P, et al. Numerical simulation to evaluate gas diffusion of turbulent flow in mine ventilation system[J].
International Journal of Mining Science & Technology, 2013, 23(3): 349-355.
|
| [16] |
王洪胜, 谭聪, 蒋仲安, 等. 综放面多尘源粉尘分布规律数值模拟及实测[J].
哈尔滨工业大学学报, 2015, 47(8): 106-112.
WANG Hongsheng, TAN Cong, JIANG Zhongan. Numerical simulation and field measurement of dust distribution under multi-source dust at fully mechanized caving face[J]. Journal of Harbin Institute of Technology, 2015, 47(8): 106-112. DOI: 10.11918/j.issn.0367-6234.2015.08.021 |
| [17] |
陈举师, 蒋仲安, 谭聪. 岩巷综掘工作面通风除尘系统的数值模拟[J].
哈尔滨工业大学学报, 2015, 47(2): 98-103.
CHEN Jushi, JIANG Zhongan, TAN Cong. Numerical simulation of dust removal and ventilation system in the rock comprehensive tunneling face[J]. Journal of Harbin Institute of Technology, 2015, 47(2): 98-103. DOI: 10.11918/j.issn.0367-6234.2015.02.018 |
 2017, Vol. 49
2017, Vol. 49


