2. 首都经济贸易大学 安全与环境工程学院, 北京 100070
2. School of Safety and Environmental Engineering, Capital University of Economics and Business, Beijing 100070, China
综采工作面中呼吸性粉尘产生和运动受多种复杂因素影响,如含尘气流不稳定因素的扰动、空间环境等的约束,导致风向和风速发生变化,影响粉尘颗粒的空间运动状态与浓度,同时壁面对粉尘的碰撞,会导致呼吸性粉尘二次飞扬,对呼吸性粉尘质量浓度在空间的分布有较大影响.
在现有的粉尘研究方面,气-固两相研究较多,常用的数学方法有欧拉法[1]、欧拉-拉格朗日法(DSMC模型[2]、DEM模型[3]等)、拉格朗日法如MaPPM模型[4].在实验方法上,谭聪等[5]根据相似准则设计了掘进巷道,分析不同条件下粉尘分布规律.在仿真模拟方面,对于流体的模拟较多采用FLUENT软件[6],基于不同的方法,如CFD-VOF-DPM[7-8],SMPLE[9],目前还有研究者采用SPH方法[10-11]进行模拟.
国内外学者对煤矿井下粉尘运移规律[12]和各种控制技术虽取得了一定研究成果,但针对两个或两个以上尘源点耦合的粉尘质量浓度分布规律的研究尚不足,对综采工作面特有环境下的呼吸性粉尘扩散模型的研究更少,早年有学者针对井巷污染物的扩散问题展开过研究,但并未考虑四周煤壁的约束,同时紊流系数的求解也未解决[13-15].
因此,本文的研究目的主要是建立适用于煤矿综采工作面的呼吸性粉尘扩散模型,并确定一套有效的求解紊流系数的方法,为煤矿综采工作面内呼吸性粉尘的治理提供更有力的理论依据.
1 综采工作面呼吸性粉尘扩散模型 1.1 气-固场耦合模型在粉尘运动中,大颗粒粉尘在气流运动中快速沉降到地面,而只有细微粉尘尤其是呼吸性粉尘则会随风飘散,难以沉降.在综采工作面中,呼吸性粉尘扩散受工作面空间以及环境等多种因素的影响和制约,呼吸性粉尘运动除了分子扩散,还包括紊流扩散和沿X轴方向的纵向弥散,使得粉尘颗粒沿纵向、横向和竖向掺混,沿风流方向散开后充满空间.由于紊流扩散系数及紊流纵向弥散系数远大于分子扩散系数,因此分子扩散系数可忽略.设紊流扩散系数为kx、ky、kz,纵向弥散系数为Ex,又Ex≫kx,根据文献[13-15],有
| $ \frac{\partial c}{\partial t}+\overline{{{u}_{x}}}\frac{\partial c}{\partial x}={{E}_{x}}\frac{{{\partial }^{2}}c}{\partial {{x}^{2}}}+{{k}_{y}}\frac{{{\partial }^{2}}c}{\partial {{y}^{2}}}+{{k}_{z}}\frac{{{\partial }^{2}}c}{\partial {{z}^{2}}}, $ | (1) |
得到式(1) 的解析解为
| $ \begin{array}{l} c\left( {x,y,z,t} \right) = \frac{M}{{{{\left( {4{\rm{\pi }}t} \right)}^{\frac{3}{2}}}{{\left( {{E_x}{k_y}{k_z}} \right)}^{\frac{1}{2}}}}}.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left[ { - \left( {\frac{{{{\left( {x - \bar ut} \right)}^2}}}{{4{E_x}t}} + \frac{{{y^2}}}{{4{k_y}t}} + \frac{{{z^2}}}{{4{k_z}t}}} \right)} \right]. \end{array} $ | (2) |
式中:c为空间某点呼吸性粉尘质量浓度;
在综采工作面进行实测限制较多,文中建立的扩散模型以相似实验模型为基础,现场应用时根据具体情况代入系数即可.在综采工作面实验模型的有限空间内,采煤机前后滚筒距离很近,假设成一个尘源,实际工作面可处理成两个不同尘源,方法不变.
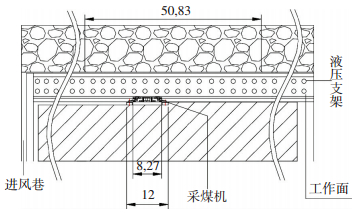
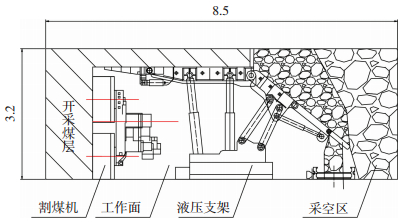
综采工作面平面图和剖面图如图 1、2所示,工作面总长285 m,建立实验模型时,截取图 1中工作面的中间段50 m为原型,按照原模比3:1搭建实验场地,即实验模型长16 m,宽2.8 m,高1.0 m.简化后的工作面实验模型如图 3所示,建立三维坐标图,以移架尘源点的中心处为坐标轴原点.
|
图 1 综采工作面平面 Figure 1 Plan of fully mechanized coal mining face |
|
图 2 综采工作面剖面 Figure 2 Profile of fully mechanized coal mining face |

|
图 3 综采工作面实验模型 Figure 3 Experimental model of fully mechanized coal mining face |
综放工作面四面煤壁会造成呼吸性粉尘二次飞扬,二次飞扬的粉尘源将作为新尘源点参与工作面扩散,假设煤壁干燥,与煤壁接触的粉尘全部二次飞扬.对二次飞扬尘源点的计算采用镜像法,即移架和割煤尘源点对称于四周煤壁有对应的虚拟源,其代替煤壁以满足二次飞扬近似求解.设尘源点坐标分别为(0,0,0),(x2,y2,z2),移架尘源点离巷道左右侧面距离均为l,距地面距离为h,则对应左侧壁的虚拟源坐标为(0,2l,0),右侧壁的虚拟源坐标为(0,-2l,0).同时,由于顶端壁面的反射在(0,0,0) 处也加一虚拟源,虚拟源和实际源的弥散和扩散强度相等,对应地面的虚拟源坐标为(0,0,-2h);割煤尘源点贴近左侧面,近似为y2=l,其虚拟源坐标分别为:对左侧壁(x2,y2,z2),对右侧壁(x2,-3l,z2),对顶壁(x2,y2,-z2),对地面(x2,y2,-h+z2).
则考虑二次飞扬后移架尘源呼吸性粉尘扩散模型表达式由式(2) 可得
| $ \begin{array}{l} {c_{z1}}\left( {x,y,z,t} \right) = \frac{{{M_1}}}{{{{\left( {4{\rm{\pi }}t} \right)}^{\frac{3}{2}}}{{\left( {{E_{x1}}{k_{y1}}{k_{z1}}} \right)}^{\frac{1}{2}}}}}.\\ \;\;\;\;\;\;\;\;\left\{ {2\exp \left[ { - \left( {\frac{{{{\left( {x - \bar ut} \right)}^2}}}{{4{E_{x1}}t}} + \frac{{{y^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right)} \right] + } \right.\\ \;\;\;\;\;\;\;\;\;\exp \left[ { - \left( {\frac{{{{\left( {x - \bar ut} \right)}^2}}}{{4{E_{x1}}t}} + \frac{{{{\left( {y - 2l} \right)}^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\exp \left[ { - \left( {\frac{{{{\left( {x - \bar ut} \right)}^2}}}{{4{E_{x1}}t}} + \frac{{{{\left( {y + 2l} \right)}^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\left. {\exp \left[ { - \left( {\frac{{{{\left( {x - \bar ut} \right)}^2}}}{{4{E_{x1}}t}} + \frac{{{y^2}}}{{4{k_{y1}}t}} + \frac{{{{\left( {z + 2h} \right)}^2}}}{{4{k_{z1}}t}}} \right)} \right]} \right\}. \end{array} $ |
因此,连续移架尘源对空间任意点在时间t内的呼吸性粉尘质量浓度总累积贡献值为
| $ \begin{array}{l} {c_{z1}}\left( {x,y,z,t} \right) = \int\limits_t {\frac{{{M_1}}}{{{{\left( {4{\rm{\pi }}t} \right)}^{\frac{3}{2}}}{{\left( {{E_{x1}}{k_{y1}}{k_{z1}}} \right)}^{\frac{1}{2}}}}}.} \\ \;\;\;\;\;\;\;\;\left\{ {2\exp \left[ { - \left( {\frac{{{{\left( {x - \bar ut} \right)}^2}}}{{4{E_{x1}}t}} + \frac{{{y^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right)} \right] + } \right.\\ \;\;\;\;\;\;\;\;\;\exp \left[ { - \left( {\frac{{{{\left( {x - \bar ut} \right)}^2}}}{{4{E_{x1}}t}} + \frac{{{{\left( {y - 2l} \right)}^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\exp \left[ { - \left( {\frac{{{{\left( {x - \bar ut} \right)}^2}}}{{4{E_{x1}}t}} + \frac{{{{\left( {y + 2l} \right)}^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\left. {\exp \left[ { - \left( {\frac{{{{\left( {x - \bar ut} \right)}^2}}}{{4{E_{x1}}t}} + \frac{{{y^2}}}{{4{k_{y1}}t}} + \frac{{{{\left( {z + 2h} \right)}^2}}}{{4{k_{z1}}t}}} \right)} \right]} \right\}{\rm{d}}t. \end{array} $ | (3) |
同理,连续割煤点的呼吸性粉尘浓度累积模型为
| $ \begin{array}{l} {c_{z2}}\left( {x,y,z,t} \right) = \int\limits_t {\frac{{{M_2}}}{{{{\left( {4{\rm{\pi }}t} \right)}^{\frac{3}{2}}}{{\left( {{E_{x2}}{k_{y2}}{k_{z2}}} \right)}^{\frac{1}{2}}}}}.} \\ \left\{ {2\exp \left[ { - \left( {\frac{{{{\left( {x - {x_2} - \bar ut} \right)}^2}}}{{4{E_{x2}}t}} + \frac{{{{\left( {y - {y_2}} \right)}^2}}}{{4{k_{y2}}t}} + \frac{{{{\left( {z - {z_2}} \right)}^2}}}{{4{k_{z2}}t}}} \right)} \right] + } \right.\\ \exp \left[ { - \left( {\frac{{{{\left( {x - {x_2} - \bar ut} \right)}^2}}}{{4{E_{x2}}t}} + \frac{{{{\left( {y + 3l} \right)}^2}}}{{4{k_{y2}}t}} + \frac{{{{\left( {z - {z_2}} \right)}^2}}}{{4{k_{z2}}t}}} \right)} \right] + \\ \exp \left[ { - \left( {\frac{{{{\left( {x - {x_2} - \bar ut} \right)}^2}}}{{4{E_{x2}}t}} + \frac{{{{\left( {y - {y_2}} \right)}^2}}}{{4{k_{y2}}t}} + \frac{{{{\left( {z + {z_2}} \right)}^2}}}{{4{k_{z2}}t}}} \right)} \right] + \\ \left. {\exp \left[ { - \left( {\frac{{{{\left( {x - {x_2} - \bar ut} \right)}^2}}}{{4{E_{x2}}t}} + \frac{{{{\left( {y - {y_2}} \right)}^2}}}{{4{k_{y2}}t}} + \frac{{{{\left( {z - {z_2} + h} \right)}^2}}}{{4{k_{z2}}t}}} \right)} \right]} \right\}{\rm{d}}t. \end{array} $ |
则连续双尘源耦合下空间任意点在时间t的呼吸性粉尘浓度平均值模型为
| $ \bar c\left( {x,y,z,t} \right) = \frac{{a{C_{z1}} + b{C_{z2}}}}{t}. $ | (4) |
式中:a、b分别为双尘源耦合系数;cz为一段时间内粉尘累积质量浓度;下标1、2分别为移架尘源与割煤尘源.
2 相似实验与紊流系数求解 2.1 相似实验 2.1.1 实验测点确定实验测点分为两组,A组测点用于求解紊流系数,B组测点用于验证准确率.如图 3所示,移架尘源点坐标为(0,0,0),割煤尘源点坐标为(3.75,1.40,-0.60),实验中测定测点风速和呼吸性粉尘质量浓度.根据实验模型尺寸和风流流场理论,A组测点在巷道风流走向的垂直方向均匀选取14个待测面,每个断面内布置5×3个待测点,共210个点;B组测点随机选取其余空间中的点,横坐标分别取1.7,3.8,6.0,8.2,10.4,13.8 m,纵坐标分别取-1.2,-0.8,0.3,1.2 m,竖坐标分别取-0.35,-0.65 m,共48个点.为避免实验误差,每组实验重复3次.
2.1.2 实验测点数据根据上述的实验方法,得到相应的实验数据,见表 1.
| 表 1 采工作面测点风速与呼吸性粉尘质量浓度值(部分) Table 1 Wind speed and the respirable dust mass concentration of measured points in similar experiment (section) |
从表 1中数据可知,实验模型内风速由于气场紊流和壁面约束影响,不同地点风速值不同,而巷道中粉尘的运移与风速关系紧密.移架与割煤耦合作用时的呼吸性粉尘质量浓度值近似为单移架和单割煤时之和,即式(4) 中,a=1,b=1,c(x, y, z, t)′=
为验证综采工作面呼吸性粉尘扩散模型的可靠性,需先求解模型中的紊流系数Ex、ky、kz,求解系数采用梯度下降法.
2.2.1 系数求解采用梯度下降法寻找参数使最小二乘损失函数最小化,其目标为实测质量浓度与预测质量浓度间误差最小化.在梯度下降算法中,定义最小二乘损失函数为:
假设L在点(x, y, z)的梯度▽L是一个向量,其方向使L增长最快,则负梯度方向使L减少最快.为求L的最小值,则沿▽L负梯度方向计算,使其达到极小点,最终求得符合条件的Ex、ky、kz.
2.2.2 求解算法由式(3),对Cz1(x, y, z, t)取对数,
| $ \begin{array}{l} \ln {c_{z1}}\left( {x,y,z,t} \right) = \int\limits_t {\left\{ {\ln {M_1} - \frac{3}{2}\ln 4{\rm{\pi }}t - \frac{1}{2}\ln {E_{x1}}{k_{y1}}{k_{z1}} + \left( { - \frac{{{{\left( {x - \bar ut} \right)}^2}}}{{4{E_{x1}}t}}} \right) + } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\ln \left[ {2{{\rm{e}}^{ - \left( {\frac{{{y^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right)}} + {{\rm{e}}^{ - \left( {\frac{{{{\left( {y - 2l} \right)}^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right)}} + {{\rm{e}}^{ - \left( {\frac{{{{\left( {y + 2l} \right)}^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right)}} + {{\rm{e}}^{ - \left( {\frac{{{y^2}}}{{4{k_{y1}}t}} + \frac{{{{\left( {z + 2h} \right)}^2}}}{{4{k_{z1}}t}}} \right)}}} \right]} \right\}{\rm{d}}t, \end{array} $ | (5) |
再将ln Cz1(x, y, z, t)分别对Ex1、ky1、kz1求导:
| $ \frac{{\partial \ln {C_{z1}}}}{{\partial {E_{x1}}}} = \int\limits_t {\left[ { - \frac{1}{{2{E_{x1}}}} + \frac{{{{\left( {x - \bar ut} \right)}^2}}}{{4tE_{x1}^2}}} \right]{\rm{d}}t} , $ | (6) |
| $ \begin{array}{l} \frac{{\partial \ln {C_{z1}}}}{{\partial {E_{y1}}}} = \int\limits_t {\left\{ { - \frac{1}{{2{k_{y1}}}} + \left\{ {\frac{{{y^2}}}{{2tk_{y1}^2}}\exp - \left( {\frac{{{y^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right) + \frac{{{{\left( {y - 2l} \right)}^2}}}{{4k_{y1}^2t}}\exp - \left[ {\frac{{{{\left( {y - 2l} \right)}^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right]} \right.} \right.} + \frac{{{{\left( {y + 2l} \right)}^2}}}{{4k_{y1}^2t}}\exp - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left[ {\frac{{{{\left( {y + 2l} \right)}^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right] + \frac{1}{{4k_{y1}^2t}}\exp - \left[ {\frac{{{y^2}}}{{4{k_{y1}}t}} + \frac{{{{\left( {z + 2h} \right)}^2}}}{{4{k_{z1}}t}}} \right]} \right\}/\left\{ {2\exp - \left( {\frac{{{y^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right) + \exp - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {\left[ {\frac{{{{\left( {y - 2l} \right)}^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right] + \exp - \left[ {\frac{{{{\left( {y + 2l} \right)}^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right] + \exp - \left[ {\frac{{{y^2}}}{{4{k_{y1}}t}} + \frac{{{{\left( {z + 2h} \right)}^2}}}{{4{k_{z1}}t}}} \right]} \right\}} \right\}{\rm{d}}t. \end{array} $ | (7) |
| $ \begin{array}{l} \frac{{\partial \ln {C_{z1}}}}{{\partial {k_{z1}}}} = \int\limits_t {\left\{ { - \frac{1}{{2{k_{z1}}}} + \left\{ {\frac{{{z^2}}}{{2tk_{z1}^2}}\exp - \left( {\frac{{{y^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right) + \frac{{{z^2}}}{{4k_{z1}^2t}}\exp - \left[ {\frac{{{{\left( {y - 2l} \right)}^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right]} \right.} \right.} + \frac{{{z^2}}}{{4k_{z1}^2t}}\exp - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left[ {\frac{{{{\left( {y + 2l} \right)}^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right] + \frac{{{{\left( {z + 2h} \right)}^2}}}{{4k_{z1}^2t}}\exp - \left[ {\frac{{{y^2}}}{{4{k_{y1}}t}} + \frac{{{{\left( {z + 2h} \right)}^2}}}{{4{k_{z1}}t}}} \right]} \right\}/\left\{ {2\exp - \left( {\frac{{{y^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right) + \exp - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {\left[ {\frac{{{{\left( {y - 2l} \right)}^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right] + \exp - \left[ {\frac{{{{\left( {y + 2l} \right)}^2}}}{{4{k_{y1}}t}} + \frac{{{z^2}}}{{4{k_{z1}}t}}} \right] + \exp - \left[ {\frac{{{y^2}}}{{4{k_{y1}}t}} + \frac{{{{\left( {z + 2h} \right)}^2}}}{{4{k_{z1}}t}}} \right]} \right\}} \right\}{\rm{d}}t. \end{array} $ | (8) |
同理,对割煤点尘源有:
| $ \frac{{\partial \ln {C_{z2}}}}{{\partial {E_{x2}}}} = \int\limits_t {\left[ { - \frac{1}{{2{E_{x2}}}} + \frac{{{{\left( {x - {x_2} - \bar ut} \right)}^2}}}{{4tE_{x2}^2}}} \right]{\rm{d}}t,} $ | (9) |
| $ \begin{array}{l} \frac{{\partial \ln {C_{z2}}}}{{\partial {k_{y2}}}} = \int\limits_t {\left\{ { - \frac{1}{{2{k_{y2}}}} + \left\{ {\frac{{{{\left( {y - {y_2}} \right)}^2}}}{{2tk_{y2}^2}}\exp - \left( {\frac{{{{\left( {y - {y_2}} \right)}^2}}}{{4{k_{y2}}t}} + \frac{{{{\left( {z - {z_2}} \right)}^2}}}{{4{k_{z2}}t}}} \right) + \frac{{{{\left( {y + 3l} \right)}^2}}}{{4k_{y2}^2t}}\exp - \left[ {\frac{{{{\left( {z - {z_2}} \right)}^2}}}{{4{k_{z2}}t}} + \frac{{{{\left( {y + 3l} \right)}^2}}}{{4{k_{y2}}t}}} \right]} \right.} \right.} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{{{{\left( {y - {y_2}} \right)}^2}}}{{4k_{y2}^2t}}\exp - \left[ {\frac{{{{\left( {y - {y_2}} \right)}^2}}}{{4{k_{y2}}t}} + \frac{{{{\left( {z + {z_2}} \right)}^2}}}{{4{k_{z2}}t}}} \right] + \frac{{{{\left( {y - {y_2}} \right)}^2}}}{{4k_{y2}^2t}}\exp - \left[ {\frac{{{{\left( {y - {y_2}} \right)}^2}}}{{4{k_{y2}}t}} + \frac{{{{\left( {z - {z_2} + h} \right)}^2}}}{{4{k_{z2}}t}}} \right]} \right\}/\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left\{ {2\exp - \left[ {\frac{{{{\left( {y - {y_2}} \right)}^2}}}{{4{k_{y2}}t}} + \frac{{{{\left( {z - {z_2}} \right)}^2}}}{{4{k_{z2}}t}}} \right] + \exp - } \right.\left[ {\frac{{{{\left( {z - {z_2}} \right)}^2}}}{{4{k_{z2}}t}} + \frac{{{{\left( {y + 3l} \right)}^2}}}{{4{k_{y2}}t}}} \right] + \exp - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {\left[ {\frac{{{{\left( {y - {y_2}} \right)}^2}}}{{4{k_{y2}}t}} + \frac{{{{\left( {z + {z_2}} \right)}^2}}}{{4{k_{z2}}t}}} \right] + \exp - \left[ {\frac{{{{\left( {y - {y_2}} \right)}^2}}}{{4{k_{y2}}t}} + \frac{{{{\left( {z - {z_2} + h} \right)}^2}}}{{4{k_{z2}}t}}} \right]} \right\}} \right\}{\rm{d}}t, \end{array} $ | (10) |
| $ \begin{array}{l} \frac{{\partial \ln {C_{z2}}}}{{\partial {k_{z2}}}} = \int\limits_t {\left\{ { - \frac{1}{{2{k_{z2}}}} + \left\{ {\frac{{{{\left( {z - {z_2}} \right)}^2}}}{{2tk_{z2}^2}}\exp - \left[ {\frac{{{{\left( {y - {y_2}} \right)}^2}}}{{4{k_{y2}}t}} + \frac{{{{\left( {z - {z_2}} \right)}^2}}}{{4{k_{z2}}t}}} \right] + \frac{{{{\left( {z - {z_2}} \right)}^2}}}{{4k_{z2}^2t}}\exp - \left[ {\frac{{{{\left( {z - {z_2}} \right)}^2}}}{{4{k_{z2}}t}} + \frac{{{{\left( {y + 3l} \right)}^2}}}{{4{k_{y2}}t}}} \right]} \right.} \right.} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{{{{\left( {z + {z_2}} \right)}^2}}}{{4k_{z2}^2t}}\exp - \left[ {\frac{{{{\left( {y - {y_2}} \right)}^2}}}{{4{k_{y2}}t}} + \frac{{{{\left( {z + {z_2}} \right)}^2}}}{{4{k_{z2}}t}}} \right] + \frac{{{{\left( {z - {z_2} + h} \right)}^2}}}{{4k_{z2}^2t}}\exp - \left[ {\frac{{{{\left( {y - {y_2}} \right)}^2}}}{{4{k_{y2}}t}} + \frac{{{{\left( {z - {z_2} + h} \right)}^2}}}{{4{k_{z2}}t}}} \right]} \right\}/\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left\{ {2\exp - \left[ {\frac{{{{\left( {y - {y_2}} \right)}^2}}}{{4{k_{y2}}t}} + \frac{{{{\left( {z - {z_2}} \right)}^2}}}{{4{k_{z2}}t}}} \right] + \exp - } \right.\left[ {\frac{{{{\left( {z - {z_2}} \right)}^2}}}{{4{k_{z2}}t}} + \frac{{{{\left( {y + 3l} \right)}^2}}}{{4{k_{y2}}t}}} \right] + \exp - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {\left[ {\frac{{{{\left( {y - {y_2}} \right)}^2}}}{{4{k_{y2}}t}} + \frac{{{{\left( {z + {z_2}} \right)}^2}}}{{4{k_{z2}}t}}} \right] + \exp - \left[ {\frac{{{{\left( {y - {y_2}} \right)}^2}}}{{4{k_{y2}}t}} + \frac{{{{\left( {z - {z_2} + h} \right)}^2}}}{{4{k_{z2}}t}}} \right]} \right\}} \right\}{\rm{d}}t. \end{array} $ | (11) |
迭代计算为
| $ \begin{array}{l} E_x^{\left( {n + 1} \right)} = E_x^{\left( n \right)} + \rho \frac{{\partial \ln {C_z}}}{{\partial E_x^{\left( n \right)}}},\\ k_y^{\left( {n + 1} \right)} = k_y^{\left( n \right)} + \rho \frac{{\partial \ln {C_z}}}{{\partial E_y^{\left( n \right)}}},\\ k_z^{\left( {n + 1} \right)} = k_z^{\left( n \right)} + \rho \frac{{\partial \ln {C_z}}}{{\partial E_z^{\left( n \right)}}}. \end{array} $ |
在Matlab7.10.0中,设定步长ρk*=0.5,学习迭代的收敛条件为10-3.式(5)~式(11) 中,l=1.4 m,h=1 m,x2=3.75 m,y2=1.4 m,z2=-0.6 m,将数据代入目标函数L的导函数进行迭代训练,共迭代910次达到收敛条件,得出:Ex1=Ex2=305.6,ky1=ky2=98.7,kz1=kz2=5.2.
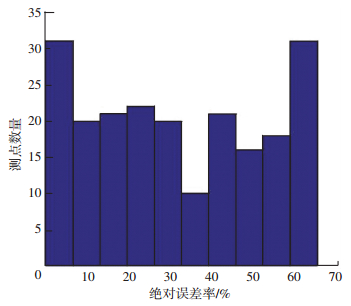
3 模型验证为验证求解系数的可靠性,采用绝对误差率作为评估指标,即将求解出的系数值代入呼吸性粉尘扩散模型中,在MATLAB中进行数据计算,L中M1=M2=60 g/min,得出各测点呼吸性粉尘质量浓度计算值,再对比实测值,得到:A组测点平均绝对误差率为31.66%,其中,35.20%测点的绝对误差率小于20%,64.70%测点的绝对误差率小于40%,其绝对误差率分布如图 4所示;B组测点的平均绝对误差率为20.94%,其中,45.83%测点的绝对误差率小于20%,91.66%测点的绝对误差率小于40%,其绝对误差率分布如图 5所示;对比258个测点,得到平均绝对误差率为29.66%.
|
图 4 A组测点理论值与实验值绝对误差率分布 Figure 4 Absolute error rates distribution of group A |

|
图 5 B组测点理论值与实验值绝对误差率分布 Figure 5 Absolute error rates distribution of group B |
图 4、5所得到的平均绝对误差率分布情况说明了呼吸性粉尘质量浓度扩散模型的有效性,也证明了紊流系数值的可靠性,表明该求解方法是可取的.
4 结论1) 在综采工作面中,呼吸性粉尘中随风流运动,四周煤壁限制粉尘的扩散,使其产生二次飞扬,二次飞扬扩散问题的解决采用镜像法.
2) 通过相似实验,分别计算出在双尘源耦合下和单一尘源时,工作面采样点的呼吸性粉尘质量浓度,并用线性回归方法确定其耦合关系.数据表明,工作面内任一点的双尘源呼吸性粉尘质量浓度值为两个独立尘源在该点的呼吸性粉尘质量浓度值之和,即耦合系数a=1,b=1.
3) 实验中258个测点分为两组,其中210个测点的风速值和呼吸性粉尘质量浓度值输入到梯度下降法中作为样本,经过不断的迭代收敛,最终得到紊流系数值.将所得值代入数学模型中,通过剩余的48个测点进行准确率验证,验证结果表明综采工作面呼吸性粉尘扩散模型紊流系数求解方法的可靠性.在实际中,可根据实际工作面尺寸、风速以及产尘量按照此方法求解紊流系数,从而得到工作面内呼吸性粉尘质量浓度分布值,为更有效的治理粉尘提供依据.
| [1] |
朱洪来, 白象忠. 流固耦合问题的描述方法及分类简化准则[J].
工程力学, 2007, 24(10): 92-99.
ZHU Honglai, BAI Xiangzhong. Description method and simplified classification rule for fluid-solid interaction problems[J]. Engineering Mechanics, 2007, 24(10): 92-99. DOI: 10.3969/j.issn.1000-4750.2007.10.017 |
| [2] |
李洁, 石于中, 徐振富, 等. 高超声速稀薄流的气粒多相流动DSMC算法建模研究[J].
空气动力学学报, 2012, 30(1): 95-100.
LI Jie, SHI Yuzhong, XU Zhenfu, et al. Study of DSMC algorithm and model for hypersonic multiphase rarefied flow[J]. Acta Aerodynamica Sinica, 2012, 30(1): 95-100. DOI: 10.3969/j.issn.0258-1825.2012.01.017 |
| [3] |
胡鹏, 黄雪莲, 吴艳兰, 等. DEM若干理论问题思考[J].
哈尔滨工业大学学报, 2006, 38(12): 2143-2147.
HU Peng, HUANG Xuelian, WU Yanlan, et al. Some problems of DEM error theory[J]. Journal of Harbin Institute of Technology, 2006, 38(12): 2143-2147. DOI: 10.3321/j.issn:0367-6234.2006.12.031 |
| [4] |
王小伟, 郭力, 唐德翔, 等. 两相体系宏观拟颗粒模拟并行算法[J].
化工学报, 2004, 55(5): 716-720.
WANG Xiaowei, GUO Li, TANG Dexiang, et al. Parallel algorithm of macro-scale pseudo-particle simulation for two-phase flow[J]. Journal of Chemical Industry and Engineering (China), 2004, 55(5): 716-720. DOI: 10.3321/j.issn:0438-1157.2004.05.009 |
| [5] |
谭聪, 蒋仲安, 王明, 等. 综放工作面多尘源粉尘扩散规律的相似实验[J].
煤炭学报, 2015, 40(1): 122-127.
TAN Cong, JIANG Zhongan, WANG Ming, et al. Similarity experiment on multi-source dust diffusion law in fully mechanized caving face[J]. Journal of China Coal Society, 2015, 40(1): 122-127. DOI: 10.13225/j.cnki.jccs.2014.0105 |
| [6] |
陈义胜, 庞赟佶, 李琛, 等. 建筑物对高架点源大气污染物扩散影响的模拟研究[J].
环境工程学报, 2010, 4(1): 47-150.
CHEN Yisheng, PANG Yunji, LI Chen, et al. Simulation study on effects of building on diffusion of air pollutants from high elevation point sources[J]. Chinese Journal of Environmental Engineering, 2010, 4(1): 47-150. |
| [7] |
LI Yong, ZHANG Jianping, FAN Liangshi. Numerical simulation of gas-liquid-solid fluidization systems using a combined CFD-VOF-DPM method: bubble wake behavior[J].
Chemical Engineering Science, 1999, 54(21): 5101-5107.
DOI: 10.1016/S0009-2509(99)00263-8 |
| [8] |
XU Yonggui, LIU Mingyan, TANG Can. Three-dimensional CFD-VOF-DPM simulations of effects of low-holdup particles on single-nozzle bubbling behavior in gas-liquid-solid systems[J].
Chemical Engineering Journal, 2013, 222: 292-306.
DOI: 10.1016/j.cej.2013.02.065 |
| [9] |
ZHANG Songbo, LV Jing. Performance analysis and numerical simulation in elliptical tubes[J].
Advanced Materials Research, 2011, 291-294: 3354-3358.
DOI: 10.4028/www.scientific.net/AMR.291-294.3354 |
| [10] |
陈福振, 强洪夫, 高巍然. 风沙运动问题的SPH-FVM耦合方法数值模拟研究[J].
物理学报, 2014, 63(13): 14-26.
CHEN Fuzhen, QIANG Hongfu, GAO Weiran. Simulation of aerolian sand transport with SPH-FVM coupled method[J]. Acta Physica Sinica, 2014, 63(13): 14-26. DOI: 10.7498/aps.63.130202 |
| [11] |
韩旭, 杨刚, 龙述尧. SPH方法在两相流动问题中的典型应用[J].
湖南大学学报:自然科学版, 2007, 34(1): 28-32.
HAN Xu, YANG Gang, LONG Shuyao. Typical application of SPH method to two-phase flow problems[J]. Journal of Hunan University(Natural Sciences), 2007, 34(1): 28-32. DOI: 10.3321/j.issn:1000-2472.2007.01.007 |
| [12] |
赵振保. 采煤机截割粉尘扩散运移规律的试验研究[J].
北京理工大学学报, 2011, 31(4): 383-386, 390.
ZHAO Zhenbao. Experimental research on diffusion and mitigation law of dust cut generated by coal shearer[J]. Journal of Beijing Institute of Technology(Natural Science Edition), 2011, 31(4): 383-386, 390. DOI: 10.15918/j.tbit1001-0645.2011.04.008 |
| [13] |
李恩良, 王秉权. 紊流扩散理论在井巷传质中的应用[J].
煤炭学报, 1988(1): 65-75.
LI Enliang, WANG Bingquan. Application of turbulent diffusion theory in mine mass transfer[J]. Journal of China Coal Society, 1988(1): 65-75. DOI: 10.13225/j.cnki.jccs.1988.01.010 |
| [14] |
李恩良. 井巷紊流传质过程的纵向弥散模型及纵向弥散系数[J].
阜新矿业学院学报, 1989, 8(3): 65-69.
LI Enliang. The longitudinal dispersion model and longitudinal dispersion coefficient of turbulent mass transfer in mine tunnel[J]. Journal of Fuxin Mining Institute, 1989, 8(3): 65-69. |
| [15] |
王鹏飞, 黄俊歆, 朱卓慧, 等. 普采工作面呼吸性粉尘浓度分布的数学模型[J].
湖南科技大学学报:自然科学版, 2010, 25(4): 21-24.
WANG Pengfei, HUANG Junxin, ZHU Zhuohui, et al. Mathematical model of the concentration distribution of respirable dust at the conventional face[J]. Journal of Hunan University of Science & Technology (Natural Science Edition), 2010, 25(4): 21-24. DOI: 10.3969/j.issn.1672-9102.2010.04.005 |
 2017, Vol. 49
2017, Vol. 49


