2. 武汉大学 水利水电学院, 武汉 430000
2. College of Water Resources and Hydropower, Wuhan University, Wuhan 430000, China
黏土在干湿循环、冻融循环及不均匀沉降的作用下极易产生裂隙[1-3],裂隙的存在为污染物(或降雨)入渗提供了重要的优势通道,从而诱发诸多工程问题.如垃圾填埋场衬垫系统开裂后,垃圾渗滤液可沿裂隙快速入渗到土壤及地下水中,造成严重的环境污染[4].降雨过程中沿裂隙的优势流可使边坡中的孔隙水压力迅速增加,边坡土强度降低,诱发滑坡等地质灾害[5].
黏土中的裂隙通常呈平板状[6],常被简化为平行板模型,利用立方定律[7]来描述沿裂隙的优势流动.裂隙中的水体与黏土之间的水量交换是优势流的一个重要影响因素.在Richard方程[8]中,裂隙与黏土之间的水量交换通过水量交换率Γw来描述, 即
| $ \frac{{\partial {\theta _{\rm{m}}}}}{{\partial t}} = \frac{\partial }{{\partial z}}\left( {{K_{\rm{m}}}\frac{{\partial {h_{\rm{m}}}}}{{\partial z}} + {K_{\rm{m}}}} \right) + \frac{{{\mathit{\Gamma }_{\rm{w}}}}}{{1-{w_{\rm{f}}}}}. $ | (1) |
式中:θm为土体的体积含水量;Km为土体的渗透系数(m/s);t为时间(s); z为距离(m); wf为裂隙率,即裂隙体积占土体总体积的百分比;Γw为水量交换率(1/s), 其物理意义是单位时间内由裂隙流入土体中的水量.式(1) 说明单位时间内土体内的体积含水量变化等于土体内的水量变化与从裂隙流入土体内的水量之和.
目前,裂隙与土体间水量交换的试验研究主要集中于砂土中的圆柱形裂隙.如Castiglion等[9]测量了圆柱形裂隙和砂土间的渗流量,利用两种介质的渗流量计算得到了裂隙与砂土之间的水量交换量.Kohne等[8]测量了两种介质接触面处的含水量变化规律.这些研究成果加强了对裂隙与土体之间水量交换的认识.然而,砂土中圆柱形裂隙的水量交换与黏土中平板形裂隙的水量交换截然不同,这主要是因为:1) 黏土中的裂隙宽度会随着土体含水量的变化而变化,当土体含水量减小时裂隙逐渐张开,裂隙宽度增加,而当土体含水量增加时,裂隙逐渐闭合,隙宽减小[10],隙宽的这种动态变化必然会引起水量交换率的变化;2) 黏土中裂隙的宽度通常为0.5~5 mm[11], 明显小于砂土中的裂隙宽度.因此,考虑黏土中裂隙的特殊性研究裂隙-黏土之间的水量交换率非常必要.
本文设计了一套测量黏土中平板裂隙水量交换的试验装置,利用张力计和含水量传感器测量裂隙周围土体中的吸力和含水量变化,从而得到其水量交换率.本文的创新点在于能够刻画动态变化的平板形裂隙与黏土之间的水量交换,反映裂隙的闭合效应对水量交换率的影响.
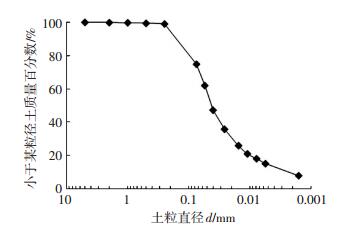
1 试验 1.1 试验用土试验用土为河北地区一处开挖场地的残积土.土体的基本物理指标如表 1所示.颗分曲线如图 1所示.根据土体的基本物理指标和颗分曲线,得出试验用土为无机低塑性黏土[12].饱和渗透系数根据《土工试验方法标准》(GB/T50123—1999) 进行测量,其中土样与下述土柱试验中的土样一致,压实度均为90%.
| 表 1 试验用土物理指标 Table 1 Physical properties of soil specimen |
|
图 1 试验用土颗粒级配曲线 Figure 1 Gradation curve for soil specimen |
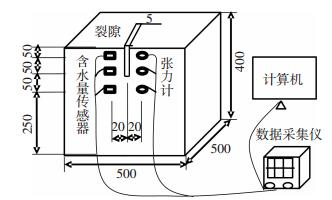
试验设备由1个全透明的有机玻璃模型箱、3个张力计和3个EC-5型含水量传感器、数据采集仪及计算机组成,如图 2所示.试验中沿模型箱中线位置制备裂隙,3个张力计和3个含水量传感器分别对称布置于裂隙两侧,张力计测量土体中的吸力变化,含水量传感器测量土体中的体积含水量变化.张力计的量程为0~90 kPa,精度为±0.25 kPa.含水量传感器的量程为0~100%,精度为满量程的±(1~2)%.
|
图 2 土柱模型装置示意图(单位:mm) Figure 2 Schematic diagram of soil column setup(unit: mm) |
黏土中的裂隙通常隙宽较小,如何制备如此细小的裂隙是本试验的挑战之一.本研究利用细铁棒结合薄铁板的方法成功制备了宽度为5 mm、深度为100 mm、长度为200 mm的人工裂隙.在压实土样过程中利用铁棒和铁板制成需要的裂隙形状,土体中的裂隙模型如图 3所示,裂隙模型由两块铁板(各厚0.7 mm)和5根铁棒(直径为3.6 mm)组成,铁夹子用于固定铁板和铁棒的位置.当土体压实到预定高度时,将图 3所示的裂隙模型放入模型箱预定位置,之后压实剩余土层.土体压实完成后,将张力计和含水量传感器安装到土体中预定位置.安装完毕后将铁棒逐根抽出,最后将铁板拿出,形成平板形裂隙.这种制备裂隙的方法保证了裂隙几何尺寸的精确,而且对裂隙周围的土体不产生扰动,传感器的安装在裂隙形成之前,也避免了安装过程对裂隙的扰动,从而保证了试验的精度,土体中制备完成的人工裂隙如图 4所示.土体中裂隙宽度为5 mm,模型箱宽度为500 mm.裂隙的宽度远小于模型箱的宽度,这样可以不考虑模型箱边界效应对裂隙与土体之间水量交换的影响.

|
图 3 土体中的裂隙模型 Figure 3 Crack model in the soil |

|
图 4 土体中的人工裂隙 Figure 4 Artificial crack in the soil |
将初始体积含水量为0.2的土体以5 cm为一层,分8层与裂隙模型一起压入模型箱,土样干密度为1.554 g/cm3.完成土样和裂隙模型压实后,将张力计和含水量传感器插入土体中,静置24 h后张力计陶瓷头完成与周围土体的水-气平衡,该段时间内需用保鲜膜密封土柱表面,防止土柱表面水分蒸发.然后逐步拆除裂隙模型.试验开始后,用高精度的注射器将水迅速充满整个裂隙,试验过程中保证裂隙一直被水充满,目的是为了维持裂隙中的恒定水压力.同时利用张力计和含水量传感器测量土体中的吸力和体积含水量变化.当裂隙闭合,传感器读数趋于稳定,裂隙两侧湿润锋(wetting front)逐渐停止扩展时, 试验结束.
2 试验结果 2.1 湿润锋随着裂隙中的水不断向土体中渗透,土体的含水量逐渐增加,同时土体的颜色随着含水量的增加而不断加深,通过观察土体颜色的变化,可以得到土体中湿润锋的变化.图 5描述了试验中裂隙周围土体中湿润锋形态的变化规律.试验进行2 min时湿润锋迅速扩散至传感器位置,湿润锋形状类似灯泡形(图 5(a)).随着试验的继续进行,湿润锋形状逐渐发生变化,由灯泡形变为抛物线形(图 5(b), (c), (d)).

|
图 5 湿润锋随时间的发展 Figure 5 Development of wetting front with 10:09:42 |
由图 5还可以看出,湿润锋在水平方向的发展快于其在竖直方向的发展,这与Allaire-Leung等[13]得到的黏土中湿润锋变化规律一致.也就是说裂隙中的水流入两侧土体后主要以水平渗透为主,这验证了Gerke等[14]的研究中水分从裂隙流入土体后主要以水平渗透为主的假设.随着试验的进行,湿润锋的扩展速度逐渐减少,当渗透40 min后,湿润锋不再扩展,趋于稳定.这与砂土中的水量交换率试验存在显著差异[15].造成这种现象的原因是黏土遇水膨胀,裂隙逐渐闭合,从而减缓了裂隙中的水向土体中的渗流,如图 6所示.图 6中裂隙两端出现明显的闭合现象,裂隙的中间部分由于溢出水流的影响形状发生了微小的改变.

|
图 6 试验结束时裂隙闭合 Figure 6 Closed crack at the end of the experiment |
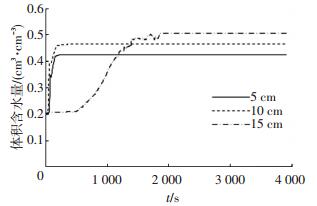
图 7描述了不同深度土体中体积含水量随时间的变化.曲线中的第一个拐点表示此深度处土体的含水量开始快速增加,说明湿润锋已经到达传感器位置.由图 7可以看出, 150 cm深度处第一个拐点出现的时间明显晚于5和10 cm深度处,说明湿润锋很快到达了5和10 cm深度处的土体,而需要经过较长时间后才到达15 cm深度处的土体.曲线中第二个拐点代表体积含水量达到稳定.裂隙周围土体的体积含水量随着入渗开始而不断增大,最后达到一个稳定值.这说明在入渗初始阶段,裂隙中的水不断渗入到土体中,导致传感器位置土体的含水量增加,当此位置土体趋于饱和后,其含水量不再增加.深度为5和10 cm处土体体积含水量迅速趋于饱和,而15 cm处体积含水量在渗透开始24 min后才达到稳定,其原因是15 cm深度处的含水量传感器位于裂隙斜下方,由于裂隙-黏土之间的水量交换主要以水平方向为主,裂隙中的水渗透到位于其下方的土体需要更长时间.
|
图 7 体积含水量随时间的变化 Figure 7 Relationship between the volumetric water content and 10:10:16 |
图 8描述了土体不同深度处吸力随时间的变化,图中每条吸力变化曲线中的第一个拐点表示不同深度处吸力开始快速降低的时刻,第二个拐点代表吸力达到稳定的时刻.裂隙周围土体吸力逐渐减小,最后达到稳定.随着张力计埋置深度的增加,其达到稳定的时间也逐渐增长,这与含水量传感器的变化一致.

|
图 8 吸力随时间的变化 Figure 8 Relationship between the matric suction and 10:10:39 |
利用不同时刻的体积含水量值可以计算得到不同时刻黏土中某点的含水量变化率, 即
| $ {\alpha _w} = \frac{{{V_{t + \Delta t}}-{V_t}}}{{\Delta t}}. $ | (2) |
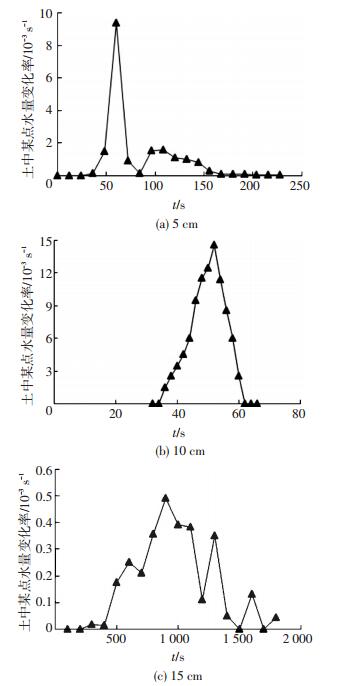
式中:Vt+Δt和Vt分别表示土中某点t+Δt时刻和t时刻的体积含水量.图 9描述了不同深度处裂隙周围土体中体积含水量的变化率,不同深度处体积含水量变化率均先增大后减小.5和10 cm处体积含水量变化率达到峰值的时间为55 s左右,深度为15 cm处体积含水量变化率达到峰值的时间为900 s.5,10和15 cm处的峰值体积含水量变化率分别为9.4×10-3,1.5×10-2和4.9×10-4 s-1.峰值体积含水量变化率在10 cm深度处最大,这是因为10 cm处土体与裂隙之间的水力梯度最大.
|
图 9 裂隙不同深度处不同时刻体积含水量变化率 Figure 9 Relationship between the water change ratio and time at different depths of the soil column |
由以上试验结果可以看出,裂隙深度为5和10 cm处体积含水量变化率达到峰值时间基本相同,裂隙深度为15 cm处含水量变化率峰值不仅相对较小且达到峰值的时间也相对滞后.从湿润锋变化规律也可以得出,深度为5和10 cm处湿润锋近似位于一条直线上,说明二者体积含水量和吸力变化趋势比较接近.因此,假设在湿润锋上土体的含水量和吸力一致.用5和10 cm两处的吸力及含水量计算裂隙的水量交换率.裂隙的水量交换率为单位时间内由裂隙流入到土体中的水量,即
| $ {\mathit{\Gamma }_{\rm{w}}} = \frac{{\Delta {V_{\rm{w}}}}}{{\Delta t \cdot \Delta V}}. $ | (3) |
式中:ΔVw为一定时间间隔内水流入土体的体积(m3),Δt为时间间隔(s),ΔV为裂隙周围土体的体积(m3).如果假设水体流入裂隙周围单位厚度的土体,则
| $ {\mathit{\Gamma }_{\rm{w}}} = \frac{{\Delta {V_{\rm{w}}}}}{{\Delta t \cdot A \cdot \Delta \omega }} = \frac{{\Delta {V_{\rm{w}}}}}{{\Delta t \cdot A}}. $ | (4) |
式中:Δω为裂隙周围土体厚度,A为裂隙与黏土接触面的总表面积(m2),另由达西定律可得
| $ k = \frac{{\Delta {V_{\rm{w}}}}}{{i \cdot A \cdot \Delta t}}. $ | (5) |
式中:k为裂隙-黏土接触面的界面渗透系数(m/s),i为裂隙边缘与传感器所在位置之间的水力梯度.i可由下式求得
| $ i = \frac{1}{2}\left( {\frac{{h_{{\rm{favr}}}^{t + \Delta t}-h_{{\rm{mavr}}}^{t + \Delta t}}}{l} + \frac{{h_{{\rm{favr}}}^t-h_{{\rm{mavr}}}^t}}{l}} \right). $ | (6) |
式中:l为裂隙边缘至传感器所在位置的距离,hfavrt为t时刻裂隙中5和10 cm两点处总压力水头的平均值(m),hmavrt为t时刻两点处土体中总压力水头(m)的平均值:
| $ h_{{\rm{mavr}}}^t = \frac{{h_{{\rm{m1}}}^t + h_{{\rm{m2}}}^t}}{2}, $ | (7) |
| $ h_{{\rm{favr}}}^t = \frac{{h_{{\rm{f1}}}^t + h_{{\rm{f2}}}^t}}{2}. $ | (8) |
式中:hm1t和hm2t分别为t时刻5和10 cm处土体中总压力水头(m),hf1t和hf2t分别为裂隙中两点处总压力水头(m).由式(4) 和(5) 可得
| $ k = \frac{{{\mathit{\Gamma }_{\rm{w}}} \cdot \Delta w}}{i} = \frac{{{\mathit{\Gamma }_{\rm{w}}}}}{i}. $ | (9) |
图 10描述了累计入渗量随时间的变化,累计入渗量随入渗时间的增加而逐渐增加,70 min时达1 500 g,然而其入渗的速度随时间的增加而逐渐减小, 由最初的100 g/min减小到最后的10 g/min.导致该现象的原因为:1) 随着裂隙周围含水量的增加裂隙逐渐闭合,减缓了水向土体中的渗量流.2) 裂隙周围土体的含水量逐渐趋于饱和,入渗逐渐减少.

|
图 10 累计入渗量随时间的变化 Figure 10 Relationship between the cumulative infiltration and 10:11:20 |
当模型箱中的土体趋于饱和,湿润锋接近模型箱的边壁时,入渗量会受边壁的限制而不断减少,因此,在计算水量交换率时,取入渗开始后20 min内的数据进行计算,此时的湿润锋距模型箱边壁较远(如图 5(b)所示),没有边界效应.根据式(4) 可以计算不同时刻的水量交换率,如图 11所示.当土体较干时,水量交换率较大,随着裂隙中的水不断渗透到土体中,水量交换率逐渐减小,最后趋于稳定,达到7.3×10-6 s-1.此结论表明Van Dam[16]将水量交换率假设成恒定值是不合理的.这主要是由于黏土中的裂隙形状随着含水量的增加而逐渐闭合,裂隙中的水并不是Novak等[10]认为的是一个稳定的水力边界条件.

|
图 11 水量交换率随时间的变化 Figure 11 Development of water exchange ratio with 10:11:36 |
由式(9) 可以计算得到裂隙-黏土之间的界面渗透系数,如图 12所示.界面渗透系数随着土体中吸力的减小而不断增大,最后达1.6×10-7 m/s.界面渗透系数大于土体的饱和渗透系数(2.32×10-8 m/s), 简单地将界面渗透系数简化为土体的渗透系数是不合理的.在Gerke等[17]的研究中,将界面渗透系数假设为裂隙渗透系数(2.3×10-4 m/s)和土体渗透系数(1.2×10-7 m/s)的算术平均值, 界面渗透系数明显大于其土体的饱和渗透系数,这一趋势与本文结论一致,然而其具体数值尚待验证.
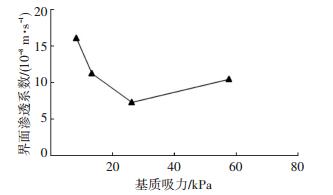
|
图 12 裂隙-黏土间界面渗透系数随基质吸力的变化 Figure 12 Change of hydraulic conductivity at clay-crack interface with matric suction |
当土体初始含水量不同时,其水量交换率也有差异.图 13显示了当土体初始体积含水量为0.2, 0.25和0.3,土体压实到相同干密度时,裂隙与土体间的水量交换率.在渗透初期,初始体积含水量为0.25 (最优含水量)的土体中的水量交换率最大,这可能是因为在相同的干密度条件下,最优体积含水量土体中的压实功最小,渗流通道相对较多.随着渗透的继续进行,由于3种不同初始体积含水量土体中的裂隙都逐渐闭合,3种土体的水量交换率趋于一致,约为7×10-6 s-1.
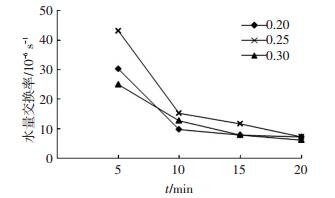
|
图 13 不同初始含水量土体中裂隙-黏土间的水量交换率 Figure 13 Development of water exchange ratio in soils with different initial water content |
1) 自行研制了一套测量黏土中平板形裂隙水量交换的试验装置.通过含水量传感器与张力计可以定量得到裂隙-黏土间的水量交换率及其界面渗透系数.
2) 裂隙-黏土间的水量交换率在渗透初期最大,随着土中基质吸力的降低而降低,这主要是因为随着土体含水量的增加,裂隙逐渐闭合,水量交换率逐渐减小.
3) 裂隙-黏土间的界面渗透系数比土体的饱和渗透系数大一个数量级,简单地将界面渗透系数简化为土体的渗透系数是不合理的.
4) 当土体的初始体积含水量接近最优含水量时,土体中的初始水量交换率最大.随着渗透的进行,不同初始含水量土体中的水量交换率趋于一致,约为7×10-6 s-1.
| [1] |
OMIDI G H, THOMAS J C, BROWN K W. Effect of desiccation cracking on the hydraulic conductivity of a compacted clay liner[J].
Water Air Soil Pollute, 1996, 89(1/2): 91-103.
|
| [2] |
BENSON C H, OTHMAN M A. Hydraulic conductivity of compacted clay frozen and thawed in suit[J].
J Geotech Engrg, 1993, 119(2): 276-294.
DOI: 10.1061/(ASCE)0733-9410(1993)119:2(276) |
| [3] |
JESSBERGER H, STONE K. Subsidence effects on clay barriers[J].
Geotechnique, 1991, 41(2): 185-194.
DOI: 10.1680/geot.1991.41.2.185 |
| [4] |
蔡武军, 凌道盛, 徐泽龙, 等. 单一裂隙优势流对黏性土层防渗性能的影响分析[J].
岩土力学, 2014, 35(10): 2838-2845.
CAI Wujun, LING Daosheng, XU Zelong, et al. Influence of preferential flow induced by a single crack on anti-seepage performance of clay barrier[J]. Rock and Soil Mechanics, 2014, 35(10): 2838-2845. |
| [5] |
谢云, 李刚, 陈正汉, 等. 复杂条件下膨胀土边坡渗流和稳定性分析[J].
后勤工程学院学报, 2006(2): 6-11.
XIE Yun, LI Gang, CHEN Zhenghan, et al. The analysis of seepage and stability for expansive soil slope under complicated environments[J]. Journal of Logistics Engineering College, 2006(2): 6-11. |
| [6] |
LI J H, ZHANG L M. Study of desiccation crack initiation and development at ground surface[J].
Engineering Geology, 2011, 123: 347-358.
DOI: 10.1016/j.enggeo.2011.09.015 |
| [7] |
SNOW D T. Anisotropic permeability of fractured media[J].
Water Resources Research, 1969, 5(6): 1273-1289.
DOI: 10.1029/WR005i006p01273 |
| [8] |
KOHNE J M, MOHANTY B P. Water flow processes in a soil column with a cylindrical macropore: Experiment and hierarchical modeling[J].
Water Resources Research, 2005, 41(3): 1-17.
|
| [9] |
CASTIGLIONE P, MOHANTY B P, SHOUSE P J, et al. Lateral water diffusion in an artificial macroporous system: modeling and experimental evidence[J].
Vadose Zone Journal, 2003, 2(2): 212-221.
DOI: 10.2136/vzj2003.2120 |
| [10] |
NOVAK B V, SIMUNEK J, GENUCHTEN VAN M T. Infiltration of water into soil with crack[J].
Journal of Irrigation and Drainage Engineering, 2000, 126: 41-47.
DOI: 10.1061/(ASCE)0733-9437(2000)126:1(41) |
| [11] |
LI J H, ZHANG L M. Geometric parametric and REV of a crack network in soil[J].
Computers and Geotechnics, 2010, 39: 466-475.
|
| [12] |
李玲. 植物根系对黏土覆盖层的影响研究[D]. 深圳: 哈尔滨工业大学深圳研究生院, 2014.
LI Ling. Effects of vegetation roots on landfill final covers[D]. Shenzhen: Shenzhen Graduate School, Harbin Institute of Technology, 2014. |
| [13] |
ALLAIRE-LEUNG S E, GUPTA S C, MONCRIEF J F. Water and solute movement in soil as influenced by macropore charateristics 1. Macropore continuity[J].
Journal of Contaminant Hydraulic, 2000, 41: 283-301.
DOI: 10.1016/S0169-7722(99)00079-0 |
| [14] |
GERKE H H, GENUCHTEN VAN M T. Macroscopic representation of structural geometry for simulating water and solute movement in dual-porosity media[J].
Advances in Water Resources, 1996, 19(6): 343-357.
DOI: 10.1016/0309-1708(96)00012-7 |
| [15] |
BAUTERS T W J, DICARLO D A, STEENHUIS T S, et al. Soil water content dependent wetting front characteristics in sands[J].
Journal of Hydrology, 2000, 2: 244-254.
|
| [16] |
DAM VAN J C. Thoery of SWAP, version 2.0. Simulation of water flow, solute transport and growth in the soil-water-atmosphere-plant environment[R]. Rep. 71, Tech. Document 45. The Netherlands: Dept. Water Resources, Wageningen Agricultural University, Dienst Landbouwkunding Onderzoek (Agricultural Research Department) Winand Staring Centre, Wageningen.
|
| [17] |
GERKE H H, GENUCHTEN VAN M T. A dual-porosity model for simulating the preferential movement of water and solutes in structured porous media[J].
Water Resources Research, 1993, 29(2): 305-319.
DOI: 10.1029/92WR02339 |
 2017, Vol. 49
2017, Vol. 49


