水下航行体高速运动过程中,当航行体周围的环境压力低于饱和蒸汽压时,航行体周围会产生明显的空化现象.空化产生的空泡发生断裂、脱落和溃灭,导致航行体表面有较大压力波动,影响航行体周围流场的稳定性,在出水过程中由于空泡的溃灭也会形成较大载荷.向空泡内人工通气不仅可以降低空化数、增加泡内压力而且可以提高空泡的稳定性.人工通气已经成为一项调节空化流场不稳定性的重要方法与技术.
国内外对于空化问题进行了大量试验研究.Reichardt[1]于1946年首次提出通过人工通气的方法生成超空泡,后来的通气空泡研究都是基于此思想;Silberman等[2]通过试验研究了通气空泡的振荡规律,得到了通气量与空泡形态和泡内压力之间的关系;Matveev等[3]通过水洞试验研究了空泡不同空化数下的稳定长度,从不同的空泡长度中分析了空泡在没有泄气和有泄气情况空泡的长度变化.黄彪等[4]通过实验研究了轴对称体空化水动力脉动特性.Ceccio[5]综合实验和数值计算对局部空泡和超空化的机理和减阻问题进行分析总结,得到通气可以使得航行体模型表面呈现气液混合状态,气泡使得航行体表面形成减阻气层.Semenenko[6]通过实验并结合理论研究通气空泡3种不同的泄气方式.Kozlov等[7]通过实验研究了通气参数对云状空泡的影响规律.Wang等[8]通过实验和数值仿真研究了航行体通气云状空化,结果表明受到空泡末端的逆压梯度影响,在回射流影响下,通气云状空化经历了断裂、脱落和溃灭等现象,并对其机理进行了分析.Dular等[9]和Stutz等[10]分别通过X射线技术研究了引起空泡非稳定性的因素.文献通过实验和数值计算分析了通气空化流场结构,分析了空泡尾部漩涡形态,也重点分析了空泡尾部回射流的的形态与形成机理[11-13].于娴娴等[14]通过数值模拟分析了通气质量流量和动量流量对空化演变过程的影响.王海滨等[15]通过水洞实验研究了水下航行体通气超空化的特性,并分析了通气空泡与重力、阻力和通气率之间的关系.邢彦江等[16]通过水洞实验分析了不同尾翼楔角对超空泡航行体阻力系数与升力系数的影响.目前针对通气空化减阻作用和稳定性的研究已经取得了很多成果,研究主要针对超空化,而对于通气局部云状空化的影响研究较少.本文利用水洞进行了水下通气航行体空泡稳定性实验研究,比较了不同空化数条件通气空泡的稳定性,分析了空化数对空泡断裂、脱落等影响.
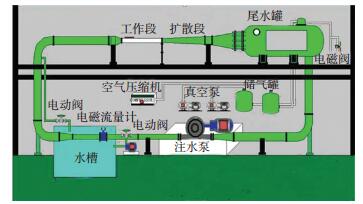
1 实验装置与方法 1.1 实验装置及模型实验主要依托哈尔滨工业大学循环式高速通气空泡水洞实验系统进行,该实验系统主要包括水洞及其操控系统, 如图 1所示,工作段的长度为1 m,横截面为260 mm×260 mm的正方形, 如图 2所示.为了便于观察工作段上、下及前、后侧面的装有透明的有机玻璃,方便通过高速摄像观察空泡形态.水洞尾水罐可以移除通气实验产生的气泡,进行长时间连续通气实验.模型及调节系统、光学测试系统、流体力测试系统以及其他辅助系统,如图 3所示.其中传感器数据线由尾支撑处引入;测力系统由安装于模型表面的传感器信号采集与记录系统等部分组成,通过压力信号可以计算该状态下模型的表面压力.不同工况水洞实验中,研究不同空化数下各不同模型对水下航行体动力特性影响时,通过调整通气质量流量和加减尾水罐压力实现水洞工作段空化数调节.
|
图 1 水洞示意 Figure 1 Schematic of water tunnel |

|
图 2 水洞工作段 Figure 2 Test section |

|
图 3 水洞实验系统示意 Figure 3 Schematic diagram of experiment water tunnel |
本实验使用的航行体模型,材质为铝合金,长度为L=315 mm,直径为D=40 mm.航行体模型内部装有7个压力传感器,实验过程中实时测得航行体表面压力,具体结构如图 4所示.

|
图 4 航行体模型 Figure 4 Vehicle model |
实验主要测量在给定空化数条件下,不同模型空化特性及流体动力特性.具体进行水洞实验时先将模型安装至水洞工作段内并调整模型为0°攻角,将摄像系统、数据采集系统以及水洞系统调试完成.实验时,调节水洞流速,在流速稳定时记录数据.实验中空化数和通气分别定义为:
| $ \begin{array}{l} \sigma = \frac{{{p_\infty }-{p_c}}}{{\frac{1}{2}\rho V_\infty ^2}}, \\ \dot m = \frac{{{Q_m}}}{{\rho {V_\infty }A}}. \end{array} $ |
式中:σ为空化数;p∞为流场远处来流压力;pc为泡内压力;ρ为流体密度;
为了研究绕航行体通气空泡的脱落特性,图 5~图 7分别给出了空化数为0.45、0.50、0.65时,通气航行体一个周期内空泡形态的发展过程.

|
图 5 空泡脱落过程(σ=0.45) Figure 5 Details of cavity shedding(σ=0.45) |

|
图 6 空泡脱落过程(σ=0.50) Figure 6 Details of cavity shedding(σ=0.50) |

|
图 7 空泡脱落过程(σ=0.65) Figure 7 Details of cavity shedding(σ=0.65) |
空泡的一个发展周期为空泡表面光滑、形成透明空泡、回射流产生、空泡脱落所经历的时间.为了更好地研究航行体的通气空泡形态随时间发展规律,不同空化数下的通气空泡发展周期分别为105、67、36 ms.对比分析不同空化数下空泡脱落速度可以看出,随着空化数的降低,航行体通气空泡的发展周期随着空化数的降低而逐渐增大.空泡断裂和脱落特性是通气空泡稳定性主要问题之一.通过空泡变化进一步研究通气航行体空泡脱落形式,图 5为σ=0.45时一个周期空泡脱落的过程,在t0+7 ms时刻可以看出附着空泡在距航行体头部约3.1 D位置处断裂,在t0~t0+14 ms时,空泡表面相对较光滑,在通气作用下空泡内的透明部分逐渐增大;在t0+19 ms~t0+46 ms时,空泡透明段发展到最大,在逆压梯度的作用下,回射流形成并向航行体前部运动,空泡前部由透明逐渐变为浑浊,在回射流的作用下空泡以U型涡团形式发生脱落.随着断裂位置上游裂痕空泡的不断发展,裂痕前后的空泡团逐渐融合在一起.当t0+46 ms时,在空泡的下游处又发生空泡断裂,断裂后的空泡再次融合.空泡的断裂、脱落、融合的发展过程,抑制了大尺度空泡团的卷起及脱落现象,取而代之的是空泡尾部小尺度空泡团的脱落溃灭过程.
图 6为σ=0.50时空泡发展图,绕航行体的空泡形态随时间的演变过程基本相同,即经历局部空泡的发展、断裂和空泡融合的过程,并且有小尺度空泡从空泡尾部脱落.通气空泡均匀地环绕在航行体肩部区域,空泡形态经历局部断裂、空泡团融合、尾部小尺度空泡断裂脱落溃灭的反复过程,空泡在距航行体头部约2.7 D位置处断裂.
从图 7可以看出,相比于σ=0.50,当σ=0.65时非定常空泡变化过程呈现出不同的空泡脱落形式.绕航行体的空泡在发展过程中空泡断裂明显并且断裂后呈现大尺度空泡团脱落,空泡在距航行体头部约2.4 D位置处断裂,空泡环绕在航行体的肩部附近,稳定性较差.当σ=0.45时,环绕在肩部的空泡表面同样会发生断裂,但是由于空泡不断融合没有大尺度空泡团脱落,而是小尺度空泡团在空泡尾部发生脱落,在空泡发展周期内有较好的稳定性.对比分析不同空化数条件下空泡断裂位置可以得到,空泡断裂位置随着空化数的增大距航行体头部距离逐渐减小, 如图 8所示.

|
图 8 空泡脱落位置 Figure 8 The position of cavity shedding |
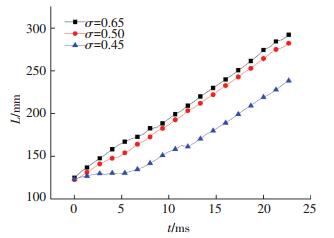
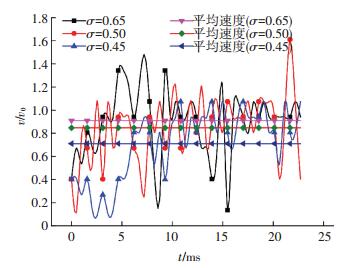
图 9、10分别统计了空化数为0.45时空泡脱落距离航行体头部的位移及对应空泡脱落速度随时间的变化.从图 9可以看出,空泡脱落位移随着时间呈线性增长趋势,由不同空化数空泡脱落速度对比可知,在σ=0.50时,位移曲线刚开始位移相对另外两个较小,说明σ=0.50时开始空泡脱落的速度较慢,如图 10所示.σ=0.65时,速度在0.40v0~1.47v0范围内波动;σ=0.50时,速度在0.11v0~1.40v0范围内波动;σ=0.45时,速度在0.10v0~1.07v0范围内波动.其中空化数σ=0.65、σ=0.50和σ=0.45的空泡平均波动速度分别为0.91、0.85、0.71.对比分析3个不同空化数的平均速度可以得到,相同速度条件下随着通气量的增加空泡平均脱落速度随着空化数的增大而减小.随着空化数的减小空泡的脱落速度比较小,这是由于小空化数下空泡断裂后不断的得到补充并连接阻碍了空泡随着水流向航行体尾部的运动.从图 10中可以看出,空泡脱落过程中受到空化数影响较大,而当空泡从整个通气空泡上脱落后速度波动基本相同.
|
图 9 脱落空泡团的运动位移随时间的变化 Figure 9 Position of cavity break-off versus 10:37:11 |
|
图 10 脱落空泡团运动的瞬时速度及平均速度 Figure 10 Instantaneous and average speeds of shedding cavities |
为了对比分析不同位置航行体表面由于空泡引起的回射、断裂、脱落引起的荷载,现通过航行体表面传感器提取航行体表面压力,并且对比分析不同位置的压力受到空泡脱落的影响.
图 11给出了空化数为0.45时不同位置航行体表面压力变化曲线.

|
图 11 不同传感器的压力 Figure 11 Pressure for different transducers |
从图 11中可以看出在一段时间内传感器T1-T7的压力波动信号,从图中可以看出T3压力传感器处的压力峰值最大并呈现周期性变化;T1和T2传感器受到回射流的影响同样呈现一定的波动,T4-T7压力传感器由于在空泡外受到空泡波动影响较小.
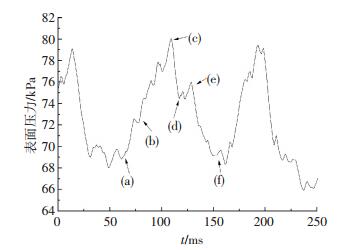
随着空泡的生长、断裂、脱落,航行体的表面空泡闭合位置压力呈现周期性波动如图 12所示,周期性波动受到回射流影响.
|
图 12 传感器T3压力曲线 Figure 12 Pressure curve of T3 transducer |
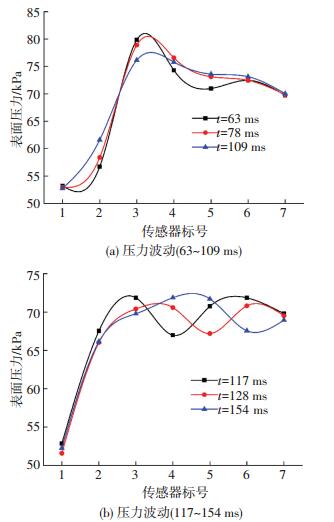
图 13为在空化数0.45时T3传感器空泡脱落,图 13(a)为空泡覆盖传感器,空泡内压力较低;图 13(b)为随着空泡末端逆压梯度的影响,回射流逐渐形成,此处的压力逐渐上升,空泡表面出现断裂;图 13(c)为空泡断裂脱落,此处压力达到最大值;图 13(d)~(e)为空泡脱落后新的空泡逐渐生长,压力逐渐降低达到最低值.图 14为图 13空泡脱落过程中航行体轴向表面压力波动曲线,图 14(a)中63、78 ms时受到空泡末端逆压梯度的影响空泡闭合位置表面压力较高,随着回射流的形成最大表面压力逐渐减小并且空泡断裂脱落如图 14(a)中109 ms所示,最后脱落空泡沿着航行体表面向后运动,航行体表面出现压力波动如图 14(b)所示.

|
图 13 工况三空泡脱落 Figure 13 The cavity shedding of condition three |
|
图 14 空泡脱落过程中航行体表面压力 Figure 14 Wall pressure with cavity shedding |
1) 通气航行体的空泡的演化过程受到通气空化数的影响.空化数较大时,空泡分为断裂、脱落两个阶段; 随着空化数的减小,空泡分为断裂、融合和脱落3个阶段.研究表明,空化数越小,空泡的发展周期越长,空泡脱落的平均速度越小,脱落后的空泡尺度越小.
2) 从实验中可以得到,随着空化数的增大,空泡断裂的位置距离航行体肩部逐渐减小,分别为3.1、2.7、2.4 D位置处.
3) 随着空泡的生长、断裂、脱落,受到回射流的影响,航行体的表面空泡闭合位置压力呈现周期性波动.
| [1] |
REICHARDT H.
The laws of cavitation bubbles at axially symmetrical bodies in a flow[M]. Gottingen: Kaiser Wilhelm Institute für Stromungsforschung, 1945: 322-326.
|
| [2] |
SLIBERMAN E, SONG C S. Instability of ventilated cavities[J].
Journal of Ship Research, 1959, 5(1): 13-33.
|
| [3] |
MATVEEV K I, MILLER M. Air cavity with variable length under a model hull[J].
Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment, 2011, 225(2): 161-169.
DOI: 10.1177/1475090211398822 |
| [4] |
黄彪, 王国玉, 权晓波, 等. 轴对称体空化水动力脉动特性的实验研究[J].
工程力学, 2012, 29(2): 239-244.
HUANG Biao, WANG Guoyu, QUAN Xiaobo, et al. Experimental study on fluctuating hydrodynamics around axisymmetric bodies[J]. Engineering Mechanics, 2012, 29(2): 239-244. |
| [5] |
CECCIO S L. Friction drag reduction of external flows with bubble and gas injection[J].
Annual Review of Fluid Mechanics, 2010, 42: 183-203.
DOI: 10.1146/annurev-fluid-121108-145504 |
| [6] |
SEMENENKO V N. Artificial supercavitation. physics and calculation[C]//Supercavitating Flows. Brussels: RTO-AVT and VKI, 2001(11):1-33.
|
| [7] |
KOZLOV I, PROKOF'EV V. Gas entrainment from a ventilated cavity with a negative cavitation number[J].
Fluid Dynamics, 2001, 36(5): 751-763.
DOI: 10.1023/A:1013072902438 |
| [8] |
WANG Yiwei, HUANG Chenguang, DU Tezhuan, et al. Shedding phenomenon of ventilated partial cavitation around an underwater projectile[J].
Chinese Physics Letters, 2012, 29(1): 014601.
DOI: 10.1088/0256-307X/29/1/014601 |
| [9] |
DULAR M, KHLIFA I, FUZIER S, et al. Scale effect on unsteady cloud cavitation[J].
Experiments in Fluids, 2012, 53(5): 1233-1250.
DOI: 10.1007/S00348-012-1356-7 |
| [10] |
STUTZ B, LEGOUPIL S. X-ray measurements within unsteady cavitation[J].
Experiments in Fluids, 2003, 35(2): 130-138.
DOI: 10.1007/S00348-003-0622-0 |
| [11] |
WANG Zhiying, HUANG Biao, WANG Guoyu, et al. Experimental and numerical investigation of ventilated cavitating flow with special emphasis on gas leakage behavior and re-entrant jet dynamics[J].
Ocean Engineering, 2015, 108: 191-201.
DOI: 10.1016/j.oceaneng,2015.07.063 |
| [12] |
段磊, 王国玉, 付细能. 绕圆头回转体通气超空化流动的实验研究[J].
兵工学报, 2014, 35(4): 475-483.
DUAN Lei, WANG Guoyu, FU Xineng. Expeimental study of ventilated supercavititating flows around a hemisphere cylinder[J]. Acta Armamentarii, 2014, 35(4): 475-483. DOI: 10.3969/j.issn.1000-1093.2014.04.007 |
| [13] |
段磊, 王国玉, 张敏弟. 绕锥头回转体通气超空化流场结构研究[J].
兵工学报, 2014, 35(12): 2058-2064.
DUAN Lei, Wang Guoyu, ZHANG Mindi. Research on flow field structure of ventilated supercavity around an axisymmetric body[J]. Acta Armamentarii, 2014, 35(12): 2058-2064. DOI: 10.3969/j.issn.1000-1093.2014.12.018 |
| [14] |
于娴娴, 王一伟, 黄晨光, 等. 通气对云状空化不稳定性调节中的控制参数与影响规律研究[J].
中国科学:物理学力学天文学, 2015, 45(3): 034703-11.
YU Xianxian, WANG Yiwei, HUANG Chenguang, et al. Parameters and influence of gas injection on modification of cavitation stability[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2015, 45(3): 034703-11. DOI: 10.1360/SSPMA2014-00334 |
| [15] |
王海斌, 王聪, 魏英杰, 等. 轴对称航行体通气超空泡的特性实验研究[J].
工程力学, 2007, 24(2): 166-171.
WANG Haibin, WANG Cong, WEI Yingjie, et al. Experimental investigation of ventilated supercavity on symmetrical underwater bodies[J]. Engineering Mechanics, 2007, 24(2): 166-171. DOI: 10.3969/j.issn.1000-4750.2007.02.028 |
| [16] |
邢彦江, 张嘉钟, 曹伟, 等. 尾翼楔角对通气超空泡特性影响试验研究[J].
哈尔滨工业大学学报, 2013, 45(1): 25-29.
XING Yanjiang, ZHANG Jiazhong, CAO Wei, et al. Experimental investigation of the effect of tail wings wedge angle on ventilated supercavity hydrodynamic[J]. Journal of Harbin Institute of Technology, 2013, 45(1): 25-29. DOI: 10.11918/hitxb20130105 |
 2017, Vol. 49
2017, Vol. 49


