高超声速飞行器一般指飞行马赫数大于5的飞行器,在军事和民用上具有巨大的应用价值.近年来,世界各国都把探索与发展高超声速技术作为航空航天领域的一个重要目标,掀起了研究和发展高超声速飞行器的热潮.高超声速飞行器所具有的高速度、强非线性、强耦合性、强不确定(随机干扰引起的不确定及弹性形变引起的不确定等)等一系列特性,都给控制上带来了极大的挑战.
高超声速飞行器弹性问题的存在,导致弹性状态与刚体状态之间产生强烈的耦合,给飞行器的控制带来了极大的困难.因此,如何解决弹性影响下的高超声速飞行器控制是控制的难点问题.另外,模型不确定问题也是飞行器控制中的一大难点,不确定分为匹配不确定与非匹配不确定.所谓匹配不确定是指不确定出现在输入通道中,反之则为非匹配不确定.解决非匹配不确定问题最常用的方法为反步控制[1],然而单纯的反步控制会导致所谓的“计算爆炸”问题.除反步控制外,滑模方法对模型不确定及外部干扰具有强鲁棒性,得到广泛应用.但传统滑模控制方法只能解决匹配不确定问题,因此,一方面,通过将滑模方法与反步控制方法结合使用[2-3],使得两者的优势相互结合,达到更好的控制效果.另一方面,随着Levant等人[4]提出干扰观测器的概念,作为对非线性系统中的外界干扰和不确定估计的有效手段,成为了研究的热点[5-7].除传统滑模外,高阶滑模控制也得到广泛的应用[8-9].文献[10]利用反馈线性化后的高超声速飞行器模型,设计观测器实现对系统未知状态的估计,并设计滑模控制器保证整个闭环系统的稳定性.如何单独利用滑模方法,基于非线性控制系统设计控制器,解决非匹配不确定问题是一个研究难点.文献[11]针对一般的带有非匹配干扰的系统,设计了基于有限时间干扰观测器的连续非奇异终端滑模面,解决了非匹配干扰问题,并应用于永磁同步电机的控制上.
本文受到文献[11]的启发,通过设计一种新型终端滑模面,将高超声速飞行器高阶非匹配问题转化为一阶匹配问题,简单有效地处理飞行器的非匹配不确定问题.
1 模型描述本文考虑的吸气式高超声速飞行器纵向动力学模型来源于文献[12]的研究成果.基于平面地球假设,将飞行器建模为一个弹性结构,推导的运动方程中包含弹性效应,同时刚体动力学和弹性动力学之间通过气动力产生耦合.高超声速飞行器纵向动力学模型为
| $ \left\{ \begin{array}{l} m\dot V = T\cos \alpha-D-mg\sin \gamma ;\\ \dot h = V\sin \gamma ;\\ \dot \gamma = \frac{{L + T\sin \alpha }}{{mV}}-\frac{g}{V}\cos \gamma ;\\ \dot \theta = Q;\\ {I_{yy}}\dot Q = M;\\ {{\ddot \eta }_i} = - 2{\zeta _i}{\omega _i}{{\dot \eta }_i} - \omega _i^2{\eta _i} + {N_i}, i = 1, 2, 3. \end{array} \right. $ | (1) |
式中:V, h, γ, θ, Q为系统的5个刚体状态,分别为速度、高度、航迹角、俯仰角以及俯仰角速率;α为攻角,
| $ \left\{ \begin{array}{l} T = \bar qS\left( {{C_T} + {C_{T\phi }}\phi + C_T^\eta \eta } \right);\\ L = \bar qS\left( {{C_L} + C_L^{{\delta _e}}{\delta _e} + C_L^\eta \eta } \right);\\ D = \bar qS\left( {{C_D} + C_D^{\delta _e^2}\delta _e^2 + C_D^{{\delta _e}}{\delta _e} + C_D^\eta \eta } \right);\\ M = {z_T}T + \bar q\bar cS\left( {{C_M} + C_M^{{\delta _e}}{\delta _e} + C_M^\eta \eta } \right);\\ {N_i} = \bar qS\left[{N_i^{{\alpha ^2}}{\alpha ^2} + N_i^\alpha \alpha + N_i^{{\delta _e}}{\delta _e} + N_i^0 + N_i^\eta \eta } \right], \\ \;\;\;\;\;\;\;\;i = 1, 2, 3. \end{array} \right. $ | (2) |
式中:
| $ \left\{ \begin{array}{l} {C_{T\phi }} = C_T^{\phi {\alpha ^3}}{\alpha ^3} + C_T^{\phi {\alpha ^2}}{\alpha ^2} + C_T^{\phi \alpha }\alpha + C_T^\phi, \\ {C_T} = C_T^3{\alpha ^3} + C_T^2{\alpha ^2} + C_T^1\alpha + C_T^0, \\ {C_L} = C_L^\alpha \alpha + C_L^0, \\ {C_D} = C_D^{{\alpha ^2}}{\alpha ^2} + C_D^\alpha \alpha + C_D^0, \\ {C_M} = C_M^{{\alpha ^2}}{\alpha ^2} + C_M^\alpha \alpha + C_M^0. \end{array} \right. $ | (3) |
式中参数具体取值见文献[13].
由于纵向动力学模型(1)~(3) 的强耦合、强不确定等特性,不适合直接进行控制器设计,因此通过将弹性与刚体之间的耦合视为综合不确定,并经过进一步的调整,可得到面向控制模型[14]为
| $ \left\{ \begin{array}{l} \dot V = {f_V} + {g_V}\phi + {\Delta _V}, \\ \dot h = V\sin \gamma, \\ {{\dot e}_\gamma } = \theta + {\Delta _\gamma }, \\ \dot \theta = Q, \\ \dot Q = {f_q} + {g_q}{\delta _e} + {\Delta _q}. \end{array} \right. $ | (4) |
式中:eγ为航迹角γ及其期望值γr之间的误差,记为eγ=γ-γr;ΔV, Δγ, Δq为综合不确定变量,其中Δγ为非匹配不确定, ΔV, Δq为匹配不确定;另外,其他系数表达为
| $ \begin{array}{l} {f_V} = \frac{{\bar qS{C_T}\cos \alpha-\bar qS{C_D}-mg\sin \gamma }}{m}, {g_V} = \frac{{\bar qS{C_{T\phi }}\cos \alpha }}{m}, \\ {f_q} = \frac{{{Z_T}\bar qS{C_T} + \bar q\bar cS{C_M}}}{{{I_{yy}}}}, {g_q} = \frac{{\bar q\bar cSC_M^{{\delta _e}}}}{{{I_{yy}}}}. \end{array} $ |
高超声速飞行器控制的目标是设计控制器ϕ, δe,使得飞行器的速度V与高度h沿着给定的参考轨迹Vr, hr飞行,保证跟踪误差在有限时间内趋于0.后续控制器设计过程中会将飞行器模型(4) 分为速度环与高度环,基于多时间尺度理论,分别进行控制器设计.
2 基于自适应律的速度环控制器设计由于本文采用的基于有限时间干扰观测器的新型非奇异终端滑模方法主要针对非匹配不确定问题,而速度环为一阶系统,并不存在非匹配不确定问题,故此处速度环采用自适应滑模方法进行控制器的设计.
由式(4) 知,速度环模型为
| $ \dot V = {f_v} + {g_v}\phi + {\Delta _V}. $ | (5) |
假设1 系统(5) 中的不确定ΔV有上界,但上界未知,即
定义速度跟踪误差为
| $ {e_V} = V-{V_r}. $ | (6) |
对式(6) 进行求导并代入式(5),可得到速度跟踪误差动态为
| $ {{\dot e}_V} = {f_V} + {g_V}\phi + {\Delta _V}-{{\dot V}_r}. $ | (7) |
控制量设计为
| $ \phi =\left[-{{f}_{V}}-{{k}_{V}}\rm{sgn} \left( {\mathit{e}_{\mathit{V}}} \right)+{{{\dot{\mathit{V}}}}_{\mathit{r}}}-{{{\hat{\bar{\Delta }}}}_{\mathit{V}}}\rm{sgn} \left( {{\mathit{e}}_{\mathit{V}}} \right) \right]/{{g}_{V}}. $ | (8) |
式中kV为大于0的常数,
| $ {{{\dot{\hat{\bar{\Delta }}}}}_{V}}=\kappa \left(-\mu {{{\hat{\bar{\Delta }}}}_{V}}+\left| {{e}_{V}} \right| \right). $ | (9) |
式中μ为大于0的常数,κ为待设计参数.
说明1 针对速度系统(5) 设计的控制器(8) 中,通过利用自适应律(9) 获得不确定上界
引理1[16] 针对系统
| $ \left\{ \begin{array}{l} \dot z = f\left( z \right), \\ f\left( 0 \right) = 0. \end{array} \right. $ | (10) |
式中z为状态量,f(z)为已知连续函数.假设存在一个连续可微的正定函数
| $ {T_{{\rm{reach}}}} \le \frac{{{\mathit{\Psi }^{1-\tau }}\left( {{z_0}} \right)}}{{\lambda {\theta _0}\left( {1-\tau } \right)}}, 0 < {\theta _0} < 1. $ | (11) |
其中Ψ(z0)为Ψ(z)的初始值.
定理1 在假设1的条件下,针对速度环动力学模型(5),选取合适的参数,则利用基于综合不确定自适应律估计(9) 的控制输入(8) 能够保证速度跟踪误差(6) 在有限时间内收敛到原点的任意小的ε-邻域内,定义Lyapunov函数
| $ {V_v} = \frac{1}{2}e_V^2 + \frac{1}{{2\kappa }}\tilde \Delta _V^2. $ | (12) |
式中
| $ {T_f} \le \frac{{\sqrt 2 V_v^{1/2}\left( 0 \right)}}{{{k_V}{\theta _0}}}. $ | (13) |
式中0 < θ0 < 1,Vv(0) 为Vv(x)的初始值.
证明 定义估计误差
| $ {{{\dot{e}}}_{V}}=-{{k}_{V}}\rm{sgn} \left( {{\mathit{e}}_{\mathit{V}}} \right)+{{\Delta }_{\mathit{V}}}-{{{\hat{\bar{\Delta }}}}_{\mathit{V}}}\rm{sgn} \left( {{\mathit{e}}_{\mathit{V}}} \right). $ | (14) |
对Lyapunov函数(12) 进行求导,可以得到
| $ \begin{matrix} {{{\dot{V}}}_{v}}={{e}_{V}}{{{\dot{e}}}_{V}}-\frac{1}{\kappa }{{{\tilde{\Delta }}}_{V}}-{{{\dot{\hat{\bar{\Delta }}}}}_{V}}= \\ -{{k}_{V}}\left| {{e}_{V}} \right|+{{e}_{V}}{{\Delta }_{V}}-{{{\hat{\bar{\Delta }}}}_{V}}\left| {{e}_{V}} \right|-{{{\tilde{\Delta }}}_{V}}\left(-\mu {{{\hat{\bar{\Delta }}}}_{V}}+\left| {{e}_{V}} \right| \right)\le \\ -{{k}_{V}}\left| {{e}_{V}} \right|+\left| {{e}_{V}} \right|\left| {{\Delta }_{V}} \right|-\left| {{e}_{V}} \right|{{{\hat{\bar{\Delta }}}}_{V}}-{{{\tilde{\Delta }}}_{V}}\left( -\mu {{{\hat{\bar{\Delta }}}}_{V}}+\left| {{e}_{V}} \right| \right)= \\ -{{k}_{V}}\left| {{e}_{V}} \right|+\left| {{e}_{V}} \right|\left( \left| {{\Delta }_{V}} \right|-{{{\bar{\Delta }}}_{V}} \right)+{{{\tilde{\Delta }}}_{V}}\left| {{e}_{V}} \right|-\\ {{{\tilde{\Delta }}}_{V}}\left( -\mu {{{\hat{\bar{\Delta }}}}_{V}}+\left| {{e}_{V}} \right| \right)\le -{{k}_{V}}\left| {{e}_{V}} \right|+\mu {{{\tilde{\Delta }}}_{V}}{{{\hat{\bar{\Delta }}}}_{V}}\le \\ -{{k}_{V}}\left| {{e}_{V}} \right|-\sqrt{\frac{\mu \left( 2\varepsilon -1 \right)}{2\varepsilon }}\tilde{\Delta }+\sqrt{\frac{\mu \left( 2\varepsilon -1 \right)}{2\varepsilon }}\tilde{\Delta }+ \\ \mu {{{\tilde{\Delta }}}_{V}}\Delta {{{\hat{\tilde{\Delta }}}}_{V}}\le -\sqrt{2}{{k}_{V}}\left( \frac{{{e}_{V}}}{\sqrt{2}}+\frac{{\tilde{\Delta }}}{\sqrt{2}\sqrt{\kappa }} \right)+\sqrt{\frac{\mu \left( 2\varepsilon -1 \right)}{2\varepsilon }}\tilde{\Delta }+ \\ \mu {{{\tilde{\Delta }}}_{V}}{{{\hat{\tilde{\Delta }}}}_{V}}\le -\sqrt{2}{{k}_{V}}V_{v}^{1/2}+\sqrt{\frac{\mu \left( 2\varepsilon -1 \right)}{2\varepsilon }}\tilde{\Delta }+\mu {{{\tilde{\Delta }}}_{V}}{{{\hat{\tilde{\Delta }}}}_{V}}. \\ \end{matrix} $ | (15) |
式中
| $ \begin{align} & \mu {{{\tilde{\Delta }}}_{V}}{{{\hat{\tilde{\Delta }}}}_{V}}=\mu {{{\tilde{\Delta }}}_{V}}\left( {{\Delta }_{V}}-{{{\tilde{\Delta }}}_{V}} \right)=\mu \left(-\tilde{\Delta }_{V}^{2}+{{{\tilde{\Delta }}}_{V}}{{\Delta }_{V}} \right)\le \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mu \left(-\tilde{\Delta }_{V}^{2}+\frac{1}{2\varepsilon }\tilde{\Delta }_{V}^{2}+\frac{\varepsilon }{2}\Delta _{V}^{2} \right)\le \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\mu \left( 1-2\varepsilon \right)}{2\varepsilon }\tilde{\Delta }_{V}^{2}+\frac{\mu \varepsilon }{2}\tilde{\Delta }_{V}^{2}. \\ \end{align} $ | (16) |
因此,式(15) 转化为
| $ \begin{align} & {{{\dot{V}}}_{v}}\le-\sqrt{2}{{k}_{V}}{{V}^{1/2}}+\sqrt{\frac{\mu \left( 2\varepsilon-1 \right)}{2\varepsilon }}{{{\tilde{\Delta }}}_{V}}+\mu {{{\tilde{\Delta }}}_{V}}{{{\hat{\tilde{\Delta }}}}_{V}}\le \\ & \ \ \ \ \ \ \ -\sqrt{2}{{k}_{V}}{{V}^{1/2}}+\frac{\mu \left( 2\varepsilon -1 \right)}{2\varepsilon }\tilde{\Delta }_{V}^{2}+\mu {{{\tilde{\Delta }}}_{V}}{{{\hat{\tilde{\Delta }}}}_{V}}\le \\ & \ \ \ \ \ \ \ -\sqrt{2}{{k}_{V}}V_{v}^{1/2}+\frac{\mu \varepsilon }{2}\Delta _{V}^{2}. \\ \end{align} $ | (17) |
根据假设1,ΔV是有界的,根据引理1可知,速度跟踪误差(6) 是有限时间收敛的,且收敛时间为
| $ {T_f} \le \frac{{\sqrt 2 V_v^{1/2}\left( 0 \right)}}{{{k_V}{\theta _0}}}. $ | (18) |
定义高度跟踪误差为
| $ {e_h} = h-{h_r}. $ |
由于航迹角γ很小,因此假设sin γ≈γ.对式(18) 进行求导,得到
| $ {{\dot e}_h} = \dot h-{{\dot h}_r} = V\sin \gamma-{{\dot h}_r} \approx V\gamma-{{\dot h}_r}. $ | (19) |
虚拟控制量γr设计为
| $ {\gamma _r} = \left( {-{k_{h1}}{e_h}-{k_{h2}}{\mathop{\rm sgn}} \left( {{e_h}} \right){{\left| {{e_h}} \right|}^\rho } + {{\dot h}_r}} \right)/V. $ | (20) |
式中kh1, kh2>0,0 < ρ < 1.
定义跟踪误差为eγ=γ-γr,将式(20) 代入式(19) 可得
| $ {{\dot e}_h} =-{k_h}{e_h} + V{e_\gamma }. $ | (21) |
因此只需eγ→0,则有eh→0,下面将设计非奇异终端滑模控制器, 使得eγ→0.
为了便于后文书写方便,定义[x1, x2, x3]=[eγ, θ, Q], [d1, d2]=[Δγ, Δq].根据式(4),eγ, θ, Q的状态方程变为
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2} + {d_1}, \\ {{\dot x}_2} = {x_3}, \\ {{\dot x}_3} = {f_q}\left( x \right) + {g_q}\left( x \right){\delta _e} + {d_2}. \end{array} \right. $ | (22) |
从式(22) 中可以看出,d1为非匹配不确定,d2与控制输入在一个通道,为匹配不确定.
假设2 d1, d2为三阶可微的,且di3(i=1, 2) 具有一组Lipschitz常数Li,即|di3|≤Li, i=1, 2[17].
参考文献[11],针对式(22) 设计一种新型的滑模面,首先定义扩展状态变量为
| $ \left\{ \begin{align} & {{{\tilde{x}}}_{1}}={{x}_{1}}, \\ & {{{\tilde{x}}}_{2}}={{x}_{2}}+{{{\hat{d}}}_{1}}, \\ & {{{\tilde{x}}}_{3}}={{x}_{3}}+{{{\hat{\dot{d}}}}_{1}}. \\ \end{align} \right. $ | (23) |
式中
| $ \left\{ \begin{array}{l} {{\dot z}_0} = {v_0} + {x_2}, \\ {v_0} =-{\lambda _0}L_1^{1/3}{\left| {{z_0}-{x_1}} \right|^{2/3}}{\mathop{\rm sgn}} \left( {{z_0}-{x_1}} \right) + {z_1}, \\ {{\dot z}_1} = {v_1}, \\ {v_1} = - {\lambda _1}L_1^{1/2}{\left| {{z_1} - {v_0}} \right|^{1/2}}{\mathop{\rm sgn}} \left( {{z_1} - {v_0}} \right) + {z_2}, \\ {{\dot z}_2} = {v_2}, \\ {v_2} = - {\lambda _2}{L_1}{\mathop{\rm sgn}} \left( {{z_2} - {v_1}} \right). \end{array} \right. $ | (24) |
式中:
定义观测器估计误差为
| $ \left\{ \begin{array}{l} \dot e_0^1 =- {\lambda _0}L_1^{1/3}{\left| {e_0^1} \right|^{2/3}}{\mathop{\rm sgn}} \left( {e_0^1} \right) + e_0^1, \\ \dot e_1^1 =- {\lambda _1}L_1^{1/2}{\left| {e_1^1- \dot e_0^1} \right|^{1/2}}{\mathop{\rm sgn}} \left( {e_1^1 - \dot e_0^1} \right) + e_2^1, \\ \dot e_2^1 \in - {\lambda _2}{L_1}{\mathop{\rm sgn}} \left( {e_2^1 - \dot e_1^1} \right) + \left[{-{L_1}, {L_1}} \right]. \end{array} \right. $ | (25) |
引理2[4] 假设观测器设计(24) 中的参数选择合理,状态量可以准确获得,那么式(25) 中的估计误差动态可以在有限时间内趋于0,即在有限时间内可以实现
设计如下非奇异终端滑模面
| $ S = {{\tilde x}_3} + \sum\limits_{i = 1}^3 {\int_0^t {{k_i}{\mathop{\rm sgn}} \left( {{{\tilde x}_i}} \right){{\left| {{{\tilde x}_i}} \right|}^{\alpha i}}{\rm{d}}\tau } } . $ | (26) |
式中ki, αi(i=1, 2, 3) 为大于0的常数.
对滑模面(26) 进行求导,得到
| $ \dot{S}={{f}_{q}}+{{g}_{q}}{{\delta }_{e}}+{{d}_{2}}+{{{\dot{\hat{\dot{d}}}}}_{1}}+\sum\limits_{i=1}^{3}{{{k}_{i}}\rm{sgn} \left( {{{\tilde{\mathit{x}}}}_{\mathit{i}}} \right){{\left| {{{\tilde{\mathit{x}}}}_{\mathit{i}}} \right|}^{\alpha {\mathit{i}}}}}. $ | (27) |
设计控制器为
| $ \begin{align} & {{\delta }_{e}}=\frac{1}{{{g}_{q}}}\left[-{{K}_{1}}S-{{K}_{2}}{{\left| S \right|}^{r}}\rm{sgn} \left( \mathit{S} \right)-{{\mathit{f}}_{\mathit{q}}}-{{{\hat{\mathit{d}}}}_{2}}-\right. \\ & \ \ \ \ \ \ \ \left. {{{\dot{\hat{\dot{d}}}}}_{1}}-\sum\limits_{i=1}^{3}{{{k}_{i}}\rm{sgn} \left( {{{\tilde{\mathit{x}}}}_{i}} \right){{\left| {{{\tilde{\mathit{x}}}}_{\mathit{i}}} \right|}^{\alpha {\mathit{i}}}}} \right]. \\ \end{align} $ | (28) |
式中K1>0, K2>0,
定理2 针对系统(22),若假设1成立,且参数选取恰当,则有限时间干扰观测器估计误差会在有限时间内趋于0,并且在控制律(28) 作用下,滑模面(26) 会有限时间内收敛,从而使得高度跟踪误差(18) 有限时间内收敛至0.
证明 将控制器(28) 代入式(27) 中,得到
| $ \dot{S}=-{{K}_{1}}S-{{K}_{2}}{{\left| S \right|}^{r}}\rm{sgn} \left( \mathit{S} \right)-\mathit{e}_{1}^{2}. $ | (29) |
式中0 < r < 1,
另外对式(23) 求导,并将式(28) 代入式(23) 可以得到
| $ \left\{ \begin{align} & {{{\dot{\tilde{x}}}}_{1}}={{x}_{2}}+{{{\hat{d}}}_{1}}-e_{1}^{1}={{{\tilde{x}}}_{2}}-e_{1}^{1}, \\ & {{{\dot{\tilde{x}}}}_{2}}={{x}_{3}}+{{{\hat{d}}}_{1}}={{{\tilde{x}}}_{3}}+{{{\tilde{e}}}_{1}}, \\ & {{{\dot{\tilde{x}}}}_{3}}={{f}_{q}}+{{g}_{q}}{{\delta }_{e}}+{{d}_{2}}+{{{\dot{\hat{\dot{d}}}}}_{1}}= \\ &-{{K}_{1}}S-{{K}_{2}}{{\left| S \right|}^{r}}\rm{sgn} \left( \mathit{S} \right)-\mathit{e}_{1}^{2}-\sum\limits_{\mathit{i}=1}^{3}{{{\mathit{k}}_{\mathit{i}}}\rm{sgn} \left( {{{\tilde{\mathit{x}}}}_{\mathit{i}}} \right){{\left| {{{\tilde{\mathit{x}}}}_{\mathit{i}}} \right|}^{\alpha {\mathit{i}}}}}. \\ \end{align} \right. $ | (30) |
式中
为了证明扩展状态变量
| $ {{V}_{1}}=\frac{1}{2}{{S}^{2}}+\sum\limits_{i=1}^{3}{\frac{1}{2}\tilde{x}_{i}^{2}}. $ | (31) |
对式(31) 进行求导,得到
| $ \begin{matrix} {{{\dot{V}}}_{1}}=S\dot{S}+{{{\tilde{x}}}_{1}}{{{\dot{\tilde{x}}}}_{1}}+{{{\tilde{x}}}_{2}}{{{\dot{\tilde{x}}}}_{2}}+{{{\tilde{x}}}_{3}}{{{\dot{\tilde{x}}}}_{3}}= \\ -{{K}_{1}}{{S}^{2}}-{{K}_{2}}{{\left| S \right|}^{r+1}}-e_{1}^{2}S+{{{\tilde{x}}}_{2}}{{{\tilde{x}}}_{2}}-e_{1}^{1}{{{\tilde{x}}}_{1}}+{{{\tilde{x}}}_{2}}{{{\tilde{x}}}_{3}}+ \\ {{{\tilde{x}}}_{2}}{{{\tilde{e}}}_{1}}+\dot{S}{{{\tilde{x}}}_{3}}-{{{\tilde{x}}}_{3}}\sum\limits_{i=1}^{3}{{{k}_{i}}\rm{sgn} \left( {{{\tilde{\mathit{x}}}}_{i}} \right){{\left| {{{\tilde{\mathit{x}}}}_{i}} \right|}^{\alpha i}}}\le \left| e_{1}^{2}S \right|+ \\ \left| {{{\tilde{x}}}_{1}}{{{\tilde{x}}}_{2}} \right|+\left| e_{1}^{1}{{{\tilde{x}}}_{1}} \right|+\left| {{{\tilde{x}}}_{2}}{{{\tilde{x}}}_{3}} \right|+\left| {{{\tilde{x}}}_{2}}{{{\tilde{e}}}_{1}} \right|+\left( {{K}_{1}}+{{K}_{2}} \right)\left| S{{{\tilde{x}}}_{3}} \right|+ \\ \left| e_{1}^{3}{{{\tilde{x}}}_{3}} \right|+\left| {{{\tilde{x}}}_{3}} \right|\sum\limits_{i=1}^{3}{{{k}_{i}}\left( 1+\left| {{{\tilde{x}}}_{i}} \right| \right)\le \frac{{{\left( e_{1}^{2} \right)}^{2}}+{{S}^{2}}}{2}}+ \\ \frac{\tilde{x}_{1}^{2}+\tilde{x}_{2}^{2}}{2}+\frac{{{\left( e_{1}^{1} \right)}^{2}}+\tilde{x}_{1}^{2}}{2}+\frac{\left( \tilde{x}_{2}^{2}+\tilde{x}_{3}^{2} \right)}{2}+\frac{\tilde{x}_{2}^{2}+\tilde{e}_{1}^{2}}{2}+ \\ \frac{\left( {{K}_{1}}+{{K}_{2}} \right)\left( {{S}^{2}}+\tilde{x}_{3}^{2} \right)}{2}+\frac{{{\left( e_{1}^{3} \right)}^{2}}+\tilde{x}_{3}^{2}}{2}+\frac{\tilde{x}_{3}^{2}+{{\left( \sum\limits_{i=1}^{3}{{{k}_{i}}} \right)}^{2}}}{2}+ \\ \frac{\sum\limits_{i=1}^{3}{{{k}_{i}}\left( \tilde{x}_{3}^{2}+\tilde{x}_{i}^{2} \right)}}{2}\le \lambda {{V}_{1}}+{{L}_{1}}. \\ \end{matrix} $ | (32) |
式中
| $ {{L}_{1}}=\frac{1}{2}\max \left\{ {{\left( e_{1}^{2} \right)}^{2}}+{{\left( e_{1}^{1} \right)}^{2}}+\tilde{e}_{1}^{2}+{{\left( e_{1}^{3} \right)}^{2}}+{{\left( \sum\limits_{i=1}^{3}{{{k}_{i}}} \right)}^{2}} \right\}. $ |
由引理2可得到,不论状态xi怎样,估计误差eji都会在有限时间内趋于0,因此L1是有界的.所以,在有限时间内状态V1不会发散到无穷,从而在干扰估计误差趋于0之前,扩展变量
当干扰估计误差在有限时间内收敛到0以后,滑模动态(29) 变为
| $ \dot{S}=-{{K}_{1}}S-{{K}_{2}}{{\left| S \right|}^{r}}\rm{sgn} \left( \mathit{S} \right). $ | (33) |
根据文献[18],系统状态会在有限时间内到达滑模面,当到达滑模面S=0时,且不确定估计误差eji=0时,系统动态(30) 变为
| $ \left\{ \begin{align} & {{{\dot{\tilde{x}}}}_{1}}={{{\tilde{x}}}_{2}}, {{{\dot{\tilde{x}}}}_{2}}={{{\tilde{x}}}_{3}}, \\ & {{{\dot{\tilde{x}}}}_{3}}=\sum\limits_{i=1}^{3}{{{k}_{i}}\rm{sgn} \left( {{{\tilde{\mathit{x}}}}_{\mathit{i}}} \right){{\left| {{{\tilde{\mathit{x}}}}_{\mathit{i}}} \right|}^{\alpha {\mathit{i}}}}\left( \mathit{i}=1, 2, 3 \right)}. \\ \end{align} \right. $ | (34) |
该系统是有限时间收敛的[19].
4 仿真分析为了说明所设计控制器的有效性,下面将进行MATLAB仿真分析.
4.1 仿真条件及参数设置针对飞行器机动爬升阶段,给定的飞行器速度的参考轨迹为由初始速度2 350 m/s经过二阶滤波器,自然频率为0.06 rad/s,阻尼为0.95,实现阶跃变化量ΔV=30.5 m/s,高度的参考轨迹为25 925 m经过同样的滤波器实现阶跃变化量Δh=610 m.控制器中参数设置分别为:k1=k2=15, k3=5,kv=3,kh1=kh2=2,ρ=0.5,K1=5, K2=0.5,α1=α2=0.65,α3=1.3,κ=2,μ=6.有限时间干扰观测器参数设置为:λ0=λ1=3,λ2=2,L1=L2=5.
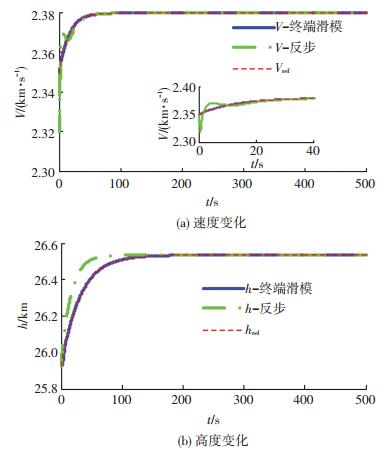
4.2 仿真结果分析在上述仿真条件下,分别利用本文的新型终端滑模及反步控制方法,完成FHV纵向爬行机动仿真实验.其仿真结果如图 1~5所示.
|
图 1 飞行器速度及高度曲线 Figure 1 Velocity and altitude of FHV |
|
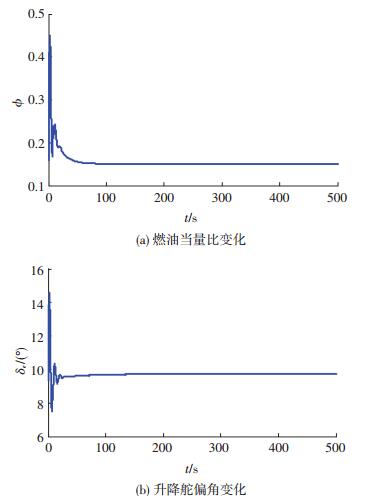
图 2 控制量变化曲线 Figure 2 Control inputs of FHV |

|
图 3 其余状态量变化曲线 Figure 3 Changes of other states |
|
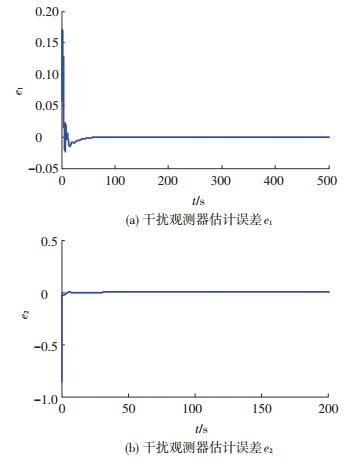
图 4 观测器估计误差变化曲线 Figure 4 Changes of estimation errors of FDO |
|
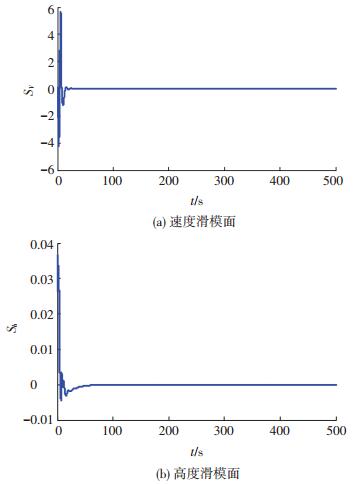
图 5 滑模面变化曲线 Figure 5 Changes of sliding mode surfaces |
从仿真结果图 1可以看出,两种方法均可实现非匹配不确定下高超声速飞行器速度与高度的稳定有效跟踪,但本文方法可以在有限时间内达到跟踪效果.当飞行器进入稳定状态后,从图 2、3可以看到,控制量与其他状态量均可以趋于稳态值,有效的抑制了弹性及不确定的影响.图 4、5表明,干扰观测器的估计误差及速度与高度滑模面均可以在有限时间内可以收敛到0.
5 结论1) 针对带弹性的高超声速飞行器的非匹配不确定问题,采用了一种基于有限时间干扰观测器的非奇异终端滑模控制策略,巧妙地在滑模面设计中加入了非匹配不确定的估计值,从而抵消其对系统稳定性的影响.
2) 该方法可以将高阶非匹配问题转化成一阶匹配问题,计算简单,有效地解决了非匹配不确定问题.且仿真结果表明,该方法设计的控制器可以实现速度与高度的有限时间稳定跟踪.
| [1] |
BU Xiangwei, WU Xiaoyan, YONG Yongxing, et al. Tracking differentiator design for the robust backstepping control of a flexible air-breathing hypersonic vehicle[J].
Journal of the Franklin Institute, 2015, 352(4): 1739-1765.
DOI: 10.1016/j.jfranklin.2015.01.014 |
| [2] |
GINOYA D, SHENDGE P D, PHADKE S B. Disturbance observer based sliding mode control of nonlinear mismatched uncertain systems[J].
Communications in Nonlinear Science and Numerical Simulation, 2015, 26(1/2/3): 98-107.
DOI: 10.1016/j.cnsns.2015.02.008 |
| [3] |
MONDAL S, MAHANTA C. Chattering free adaptive multivariable sliding mode controller for systems with matched and mismatched uncertainty[J].
ISA Transactions, 2013, 52(3): 335-341.
DOI: 10.1016/j.isatra.2012.12.007 |
| [4] |
SHTESSEL Y B, SHKOLNIKOV I A, LEVANT A. Smooth second-order sliding modes: missile guidance application[J].
Automatica, 2007, 43(8): 1470-1476.
DOI: 10.1016/j.automatica.2007.01.008 |
| [5] |
SUN Haibin, GUO Lei. Composite adaptive disturbance observer based control and back-stepping method for nonlinear system with multiple mismatched disturbances[J].
Journal of the Franklin Institute, 2014, 351(2): 1027-1041.
DOI: 10.1016/j.jfranklin.2013.10.002 |
| [6] |
SUN Haibin, LI Shihua, YANG Jun, et al. Non-linear disturbance observer-based back-stepping control for airbreathing hypersonic vehicles with mismatched disturbances[J].
IET Control Theory and Applications, 2014, 8(17): 1852-1865.
DOI: 10.1049/iet-cta.2013.0821 |
| [7] |
WANG Na, WU Huaining, GUO Lei. Coupling-observer-based nonlinear control for flexible air-breathing hypersonic vehicles[J].
Nonlinear Dynamics, 2014, 78(3): 2141-2159.
DOI: 10.1007/s11071-014-1572-1 |
| [8] |
WANG Jie, ZONG Qun, TIAN Bailing, et al. Flight control for a flexible air-breathing hypersonic vehicle based on quasi-continuous high-order sliding mode[J].
Journal of Systems Engineering and Electronics, 2013, 24(2): 288-295.
DOI: 10.1109/JSEE.2013.00036 |
| [9] |
宗群, 苏芮, 王婕, 等. 高超声速飞行器自适应高阶终端滑模控制[J].
天津大学学报(自然科学与工程技术版), 2016, 47(11): 1031-1037.
ZONG Qun, SU Rui, WANG Jie, et al. Adaptive high-order terminal sliding mode control for hypersonic flight vehicle[J]. Journal of Tianjin University(Science and Technology), 2016, 47(11): 1031-1037. DOI: 10.11784/tdxbz201309014 |
| [10] |
MU Chaoxu, SUN Changyin, YU Xinghuo. Observation and control for air-breathing hypersonic aircrafts based on sliding mode method[C]// Conference on IEEE Industrial Electronics Society. Melbourne: IEEE Press, 2011:3965-3970.DOI: 10.1109/IECON.2011.6119957.
|
| [11] |
YANG Jun, LI Shihua, SU Jinya, et al. Continuous nonsingular terminal sliding mode control for systems with mismatched disturbances[J].
Automatica, 2013, 49(7): 2287-2291.
DOI: 10.1016/j.automatica.2013.03.026 |
| [12] |
FIORENTINI L. Nonlinear adaptive controller design for air-breathing hypersonic vehicles[D]. Columbus: The Ohio State University, 2010.
http://www2.ece.ohio-state.edu/~fiorentini/Biography_files/Fiorentini_CV_1.pdf
|
| [13] |
YE Linqi, ZONG Qun, ZHANG Xiuyun. Adaptive control for a non-minimum phase hypersonic vehicle model[C]//2015 34th Chinese Control Conference (CCC). Hangzhou: IEEE Press, 2015: 991-996.DOI: 10.1109/ChiCC.2015.7259769.
|
| [14] |
ZONG Qun, WANG Fang, TIAN Bailing, et al. Robust adaptive dynamic surface control design for a flexible air-breathing hypersonic vehicle with input constraints and uncertainty[J].
Nonlinear Dynamics, 2014, 78(1): 289-315.
DOI: 10.1007/s11071-014-1440-z |
| [15] |
ZHU Zheng, XIA Yuanqing, FU Mengyin. Attitude stabilization of rigid spacecraft with finite-time convergence[J].
International Journal of Robust and Nonlinear Control, 2011, 21(6): 686-702.
DOI: 10.1002/rnc.1624 |
| [16] |
TIAN Bailing, SU Rui, FAN Wenru. Multiple-time scale smooth second order sliding mode controller design for flexible hypersonic vehicles[J].
Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2014: 0954410014539466.
DOI: 10.1177/0954410014539466 |
| [17] |
LI Shihua, TIAN Y P. Finite-time stability of cascaded time-varying systems[J].
International Journal of Control, 2007, 80(4): 646-657.
DOI: 10.1080/00207170601148291 |
| [18] |
BHAT S P, BERNSTEIN D S. Finite-time stability of continuous autonomous systems[J].
SIAM J on Control and Optimization, 2000, 38(3): 751-766.
DOI: 10.1137/S0363012997321358 |
| [19] |
BHAT S P, BERNSTEIN D S. Geometric homogeneity with applications to finite-time stability[J].
Mathematics of Control, Signals and Systems, 2005, 17(2): 101-127.
DOI: 10.1007/s00498-005-0151-x |
 2017, Vol. 49
2017, Vol. 49


