2. 武汉大学 动力与机械学院, 武汉 430072
2. Shool of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China
借助浅剖仪的换能器发射的声波在海底不同介质面发生的反射信号,可以获得浅剖图像[1-8].但受复杂海底环境、多样性底质和声波在层界间多次反射造成的多次波干扰等影响,清晰的浅剖图像难以得到,基于一般的图像处理技术很难实现层界的准确、连续划分[9].为此,本文结合浅剖Ping(一个完整的声波发射—接收过程)回波强度时序特点、多Ping构成的图像的复杂程度以及层界变化的连续性,提出了一种顾及图像信息熵[10-12]的浅地层层界划分方法,以期消除诸因素影响,实现层界的自适应、准确划分.
1 浅地层剖面图像生成及其预处理 1.1 图像生成浅地层剖面仪(浅剖)测量中,换能器接收到的时序回波强度数据常以二进制的SEG-Y格式文件存储,为获得浅地层数字图像,需首先对其解码[13-14].由于接收信号常以相对发射声波振幅形式记录,需借助Hilbert变换才能获得接收信号的实际振幅或强度[15].
为提高数据质量,对Hilbert变换获得的声强进行截取有效声强、剔除无效数据、声强集中部分拉伸等处理.结合走航过程中每Ping的平面位置、测量中每个回波的深度,在地理框架下即可得到浅地层剖面图像.
1.2 图像预处理受海洋环境、声波传播机制等影响,浅剖换能器接收到的回波数据中存在Ping丢失、噪声和多次波等干扰,导致图像质量偏低,为此需对原始图像开展如下预处理.
1) Ping修复.基于底质结构变化的连续性,根据丢失Ping前后Ping中的有效Ping数据,采用均值内插或基于底质渐变原则的多项式模型内插,实现丢失Ping修复.
2) 噪声抑制.中值滤波具有不损失特征边缘、对噪声消除彻底等特点,可用于抑制浅剖图像中的噪声,提高图像质量.
3) 多次波压制.利用多次波的周期性特征,通过设计预测误差滤波器,基于预测反褶积法削弱多次波影响[16].
2 层界划分基本原理 2.1 基于Ping回波时序强度变化特点的层界峰谷划分方法根据水声学原理,Ping声信号在进入不同介质的层界面时会产生强反射,在浅地层图像中则表现为灰度突变;而在层界间,由于底质近似,回波强度接近,图像中则表现为灰度均匀变化.根据以上特点,在每Ping形成的列灰度序列中定义一个由一定数量采样点的灰度值组合形成的统计窗口,并给出如下5个层界划分原则.
1) 灰度陡变点为对应统计窗口内的峰值点.
2) 灰度陡变点有足够的显著性.对于第m个检验点,定义检验模型为
| $ G\left( m \right)-\mu > k\sigma . $ |
式中:G(m)为第m个检验点的灰度值,统计窗口的范围为(m-10,m+10); k为中误差系数; μ、σ分别为统计窗口内灰度的均值、标准差.
3) 考虑声能随传播距离衰减,后一个峰值点灰度值应小于前一个.
另外由于浅地层剖面测量时受到来自海洋、仪器、多次波等各类噪声的影响,使得单Ping灰度曲线变化剧烈,存在众多噪声点或伪层界.为削弱这些影响,达到提取真实层界的目的,本文采用N Ping均值滤波方法,即认为在N Ping变化范围内层界是连续的、结构近似一致.在参与平均的Ping数选择时,应遵循如下2个原则.
4) 涵盖的范围不能太大,避免出现层界细部信息丢失.
5) 涵盖的范围不能太小,否则不能达到噪声压制效果.
基于以上5个原则,对每Ping开展层界划分, 将相邻Ping相同层界连接,获得整个图像中的层界及其分布.
2.2 图像二维信息熵以上层界峰谷划分法中,中误差系数k及参与平均的Ping数N的确定问题需要解决.k和N均与图像中灰度变化的复杂程度、噪声、层界图像的显著程度等密切相关.为此引入图像二维信息熵,以期实现上述2个参数的自适应确定.
2.3 N、k与V关系建立获得二维熵V后,可以根据钻孔取芯数据提供的真实层界为参考,结合对应层界的图像二维熵V,以及基于不同N和k下层界的划分结果,构建彼此间的关系模型.
1)N、k和V参数集确定.为方便计算,首先将整个图像根据钻孔位置划分成若干区块,区块大小为S,并提取S对应图像的二维熵V;然后在一个区块内,不断改变N和k,借助层界峰谷划分法开展层界划分;以钻孔数据为参考,获得划分层界与实际层界一致时的N、k及V;在不同区块开展上述工作,最终形成N、k和V构成的集合.{N,k,V}集合的寻找过程如图 1所示.
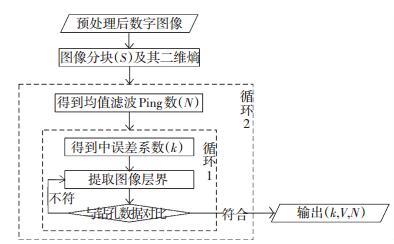
|
图 1 k,V,N确定流程 Figure 1 Flow chart for determination of k, V and N |
2) 利用{N,k,V}集合绘制三维图,根据N和V在三维图中的变化曲线,发现变化拐点,结合最大信息熵原则,最终确定N.
3) 根据输出的{N,k,V}序列,分析k随N的变化及成因.
考虑k、V变化特点,采用高斯拟合函数建立k-V关系模型为
| $ \begin{array}{l} k = f\left( V \right) = {a_1}{{\rm{e}}^{-{{\left( {\frac{{\left( {V-{b_1}} \right)}}{{{c_1}}}} \right)}^2}}} + {a_2}{{\rm{e}}^{-{{\left( {\frac{{\left( {V - {b_2}} \right)}}{{{c_2}}}} \right)}^2}}} + \cdots + \\ {a_8}{{\rm{e}}^{ - {{\left( {\frac{{\left( {V - {b_8}} \right)}}{{{c_8}}}} \right)}^2}}}, \end{array} $ | (1) |
式中,ai、bi、ci (i=1, 2, …, 8) 分别为模型系数.与传统的多项式拟合相比,高斯拟合采用高斯函数系,具有收敛快、拟合准确等特点.根据实际拟合情况,本文采用式(1) 所示8项高斯叠加函数作为k-V关系模型.
基于式(1) 给出的k-V关系模型及N-V关系,在不同的子区,根据对应的图像二维熵可得相应的N及k值,据此借助层界峰谷划分法实现层界划分.
3 层界划分流程根据以上原理,基于图像二维信息熵约束的浅地层层界划分流程如下, 如图 2所示.
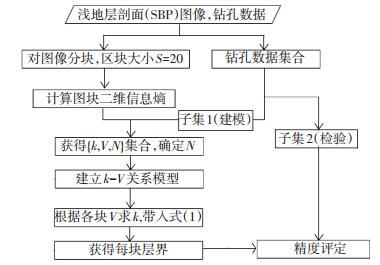
|
图 2 层界划分流程 Figure 2 Flow chart for demarcation of layers |
为验证上述方法的正确性,在烟台某水域借助C-Boom浅地层剖面仪开展了1个航次的浅地层剖面测量和钻孔取芯工作.测量中,C-Boom的采样频率为4 Hz,船速为4~5节,Ping间隔约为0.5 m.走航断面平均设有7个钻孔点,经实验室分析得到所在位置的浅地层层界.
对浅地层剖面观测数据分别开展SEG-Y格式原始文件解码和转换,并开展Ping修复、消噪和多次波压制等图像预处理.预处理后的图像如图 3所示.
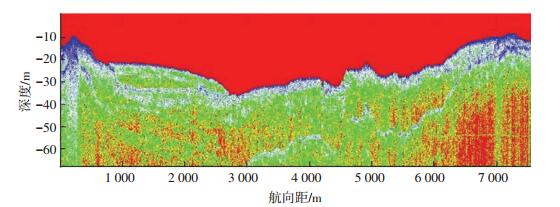
|
图 3 预处理后的浅地层剖面 Figure 3 Sub-bottom profile image after data preprocessing |
选择4个代表性钻孔,在对应位置划分区块,根据各区块的V、N及k构建{N,k,V}集合,并绘制如图 4所示图形.可以看出:1) 整体上N越大V越小.分析认为随着N变大,滤波所得图像细节信息损失,导致V减小.在N为35~40区间出现不一致现象.该现象主要是由于当N超过图像区块大小S时,方法将S放大进而造成V增大; 2)V越大k越大.主要由于V增大,层界提取时图像中的信息量就越大,只有选取较大的k才能界定峰点.
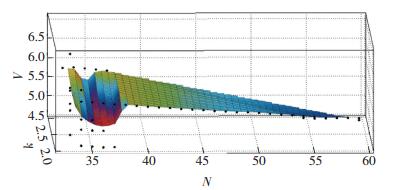
|
图 4 {k, V, N}集合三维分布 Figure 4 3-dimension distribution of {N, k, V} |
以上仅定性分析了三者间关系,下面定量确定彼此间关系.考虑直接建立N-k-V关系模型比较复杂,为简化问题,首先确定N,然后构建k-V模型.
从图 4可看出,N≤35时N增大V减小;N在36~37区间时N增大V增大;N>37时N增大V减小.因此,两者关系在35~40间存在两个拐点:35和37.考虑层界处图像灰度会产生突变,信息熵会较大,取N=37,此处V最大,同时还兼顾了N与V之间的两个关系.
为验证上述结论,让k=2.5,变化N从2到60,对不同N下所得平均Ping灰度序列,借助峰谷法提取层界, 如图 5所示.从图 5可看出:N越小,提取出的层界越不准确;随着N增大,层界变得越来越接近钻孔层界位置;但随N进一步增大,层界位置逐渐变得模糊,最终偏离实际.以上关系变换的拐点即在N=37,与图 4给出的结论一致.
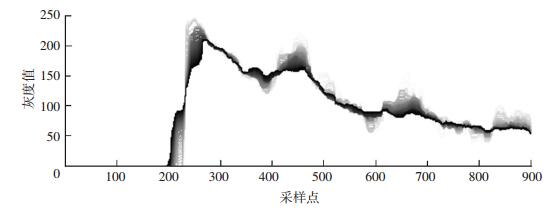
|
图 5 N与层界划分准确性关系曲线 Figure 5 Relationship curve of N and sub-bottom layer division |
N确定后,提取出{N,k,V}集中的{k,V}集,将之绘制到图 6中,并利用这些数据构建k-V关系模型,模型参数和模型曲线如表 1和图 6所示.可以看出,模型内符合精度较高,RMSE达到0.006 8;拟合曲线与实际非常吻合,表明确定的模型参数真实可靠.
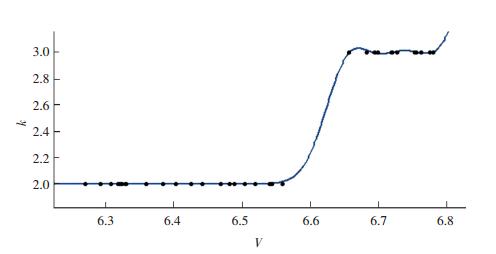
|
图 6 k-V关系曲线 Figure 6 k-V relationship curve |
| 表 1 确定的高斯模型参数及精度 Table 1 Gauss model's coefficient and model accuracy |
计算其他3个未参与建模钻孔位置对应区块的V,依据上述模型得到各区块的N及k.同样借助图 1所示流程,得到这3个区块对应的N0和k0,并将V对应的k0绘制到图 7中.从图 7可以看出,基于模型得到k-V变化曲线与实际k0取得了一致,同时N-V关系得到的N与N0相同,进一步表明基于上述方法得到的N-V关系以及k-V关系模型适用于整个图像.
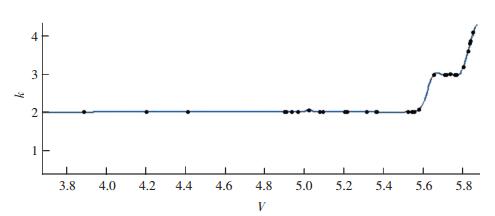
|
图 7 k-V关系模型与k0的比较 Figure 7 Comparison of the k0 from k-V model and those from drilling data |
得到可靠的N-V关系及k-V关系模型后,便可进行层界划分.首先进行分块,S为平均N的2倍;然后计算不同区块的V,N和k;采用逐Ping遍历法,对每一Ping对应的灰度序列基于峰谷法开展层界提取,完成所有区块层界划分;最后,将相邻层界连接,获得整个层界.比较图 8和图 3可看出,相对原始图像,本文方法划分出的层界真实、清晰.
|
图 8 划分出的层界分布图 Figure 8 Distribution of sub-bottom layers |
为定量评估本文方法的正确性及精度,以钻孔给出的层界为参考,将上述划分层界与之比较(如图 9所示),划分层界位置及层厚度偏差统计结果如表 2所示.从图 9可以看出,二者吻合较好;表 2中的统计结果表明,二者的层界深度偏差最大绝对值小于20 cm,厚度偏差最大绝对值小于30 cm,与钻孔数据的给出的层界精度(分米级)处同量级,表明本文给出的方法不但实现了层界的自适应划分,层界划分的精度也满足了工程需要.
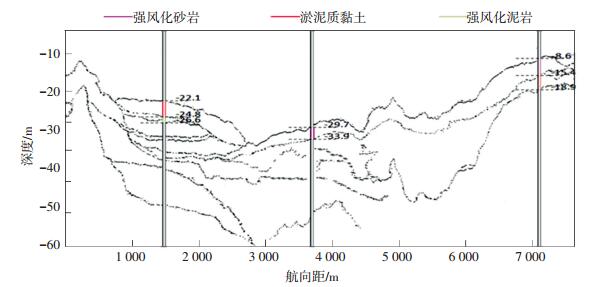
|
图 9 用于检验层界提取的钻孔位置 Figure 9 Sub-bottom layers and the 3 drilling locations for checking layer's extraction |
| 表 2 划分层界深度及层厚度与钻孔资料的偏差 Table 2 Biases of layer' position and thickness determined by layer extraction relative to the drilling data |
1) 浅剖图像的预处理(包括修复、去噪、压制多次波等),可提高图像信噪比,得到层界较清晰的浅剖图像.该环节得到的图像质量直接影响后续浅剖层界自动提取的效果.
2) 根据浅剖层界位置处,Ping灰度值突变原理提取层界,实现了浅剖层界提取自动化.但该方法需要一个准确的显著性系数k来界定灰度突变点,以期实现浅剖层界的准确提取.
3) 采用二维图像信息熵作为约束,即根据不同区块的不同信息熵值设置显著性系数k,提高了浅剖层界提取的准确性,减少了图像细节信息的损失,避免了强噪声或伪层界造成的干扰,实现了智能化、自动化提取真实层界的目的.
| [1] |
李斌, 杨文达, 张异彪, 等. 海底管道的浅地层剖面图上反射特征与判读方法[J].
海洋测绘, 2010, 30(5): 56-58.
LI Bin, YANG Wenda, ZHANG Yibiao, et al. Characteristics of the seabed pipeline's reflection in the sub-bottom profiling and interpretation[J]. Hydrographic Surveying and Charting, 2010, 30(5): 56-58. DOI: 10.3969/j.issn.1671-3044.2010.05.016 |
| [2] |
HONSHO C, URA T, ASADA A, et al. High-resolution acoustic mapping to understand the ore deposit in the Bayonnaise knoll caldera, Izu-Ogasawara arc[J].
Journal of Geophysical Research: Solid Earth, 2015, 120(4): 2070-2092.
DOI: 10.1002/2014JB011569 |
| [3] |
王方旗. 浅地层剖面仪的应用及资料解译研究[D]. 青岛: 国家海洋局第一海洋研究所, 2010.
WANG Fangqi. The research of the application and data interpretation of sub-bottom profiler[D]. Qingdao: The First Institute of Oceanography, SOA, 2010. http://www.doc88.com/p-6012089961280.html |
| [4] |
MACLEAN B, BLASCO S, BENNETT R, et al. New marine evidence for a Late Wisconsinan ice stream in Amundsen Gulf, Arctic Canada[J].
Quaternary Science Reviews, 2015, 114: 149-166.
DOI: 10.1016/j.quascirev.2015.02.003 |
| [5] |
PLETS R M K, DIX J K, ADAMS J R, et al. The use of a high-resolution 3D Chirp sub-bottom profiler for the reconstruction of the shallow water archaeological site of the Grace Dieu (1439), River Hamble, UK[J].
Journal of Archaeological Science, 2009, 36(2): 408-418.
DOI: 10.1016/j.jas.2008.09.026 |
| [6] |
CARLIN J A, DELLAPENNA T M, STROM K, et al. The influence of a salt wedge intrusion on fluvial suspended sediment and the implications for sediment transport to the adjacent coastal ocean: a study of the lower Brazos River TX, USA[J].
Marine Geology, 2015, 359: 134-147.
DOI: 10.1016/j.margeo.2014.11.001 |
| [7] |
BAETEN N J, LABERG J S, VANNESTE M, et al. Origin of shallow submarine mass movements and their glide planes-Sedimentological and geotechnical analyses from the continental slope off northern Norway[J].
Journal of Geophysical Research: Earth Surface, 2014, 119(11): 2335-2360.
DOI: 10.1002/2013JF003068 |
| [8] |
HAO Yanjun, MCINTOSH K, MAGNANI MB. Long-lived deformation in the southern Mississippi Embayment revealed by high-resolution seismic reflection and sub-bottom profiler data[J].
Tectonis, 2015, 34(3): 555-570.
DOI: 10.1002/2014TC003750 |
| [9] |
张恒超. 几种简单实用的多次波去除方法及其应用[J].
内蒙古石油化工, 2011(21): 21-24.
ZHANG Hengchao. Several practical methods of multiple waves suppression and their applications[J]. Inner mongulia petrochemical industry, 2011(21): 21-24. DOI: 10.3969/j.issn.1006-7981.2011.21.010 |
| [10] |
华长发, 范建平, 高传善, 等. 基于二维熵阈值的图像分割及其快速算法[J].
模式识别与人工智能, 2000, 13(1): 42-46.
HUA Changfa, FAN Jianpin, GAO Chuanshan, et al. Image segmentation based on 2d entropic thresholding and its fast algorithm[J]. Pattern Recognition and Artificial Intelligence, 2000, 13(1): 42-46. DOI: 10.3969/j.issn.1003-6059.2000.01.009 |
| [11] |
吴泽鹏, 郭玲玲, 朱明超, 等. 结合图像信息熵和特征点的图像配准方法[J].
红外与激光工程, 2013, 42(10): 2846-2852.
WU Zepeng, GUO Lingling, ZHU Mingchao, et al. Improved image registration using feature points combined with image entropy[J]. Infrared and Laser Engineering, 2013, 42(10): 2846-2852. DOI: 10.3969/j.issn.1007-2276.2013.10.046 |
| [12] |
GABARDA S, CRISTOBAL G. The generalized Renyi image entropy as a noise indicator-art[C]// Proceedings of the SPIE 6603, Noise and Fluctuations in Photonics, Quantum Optics, and Communications. Florence: SPIE, 2007. DOI: 10.1117/12.725086.
|
| [13] |
王增波, 李雁鸿, 赵剑, 等. SEG-Y地震数据格式解析及转换方法[J].
物探装备, 2012, 22(3): 177-182.
WANG Zengbo, LI Yanhong, ZHAO Jian, et al. Analytical method and conversion method for SEG-Y data[J]. Equipment for Geophysical Prospecting, 2012, 22(3): 177-182. DOI: 10.3969/j.issn.1671-0657.2012.03.010 |
| [14] |
肖梅, 刘国华, 李庆春. 在VC++环境下读取地震勘探SEG-Y格式数据及其应用[J].
中国科技信息, 2005(9): 17-17, 29.
DOI: 10.3969/j.issn.1001-8972.2005.09.012 |
| [15] |
李枝文, 宋伟, 肖柏勋, 等. Hilbert变换与小波变换在探地雷达资料处理中的应用[J].
工程地球物理学报, 2012, 9(4): 428-432.
LI Zhiwen, SONG Wei, XIAO Boxun, et al. Application of hilbert transform and wavelet transform to data processing of ground penetrating radar[J]. Chinese Journal of Engineering Geophysics, 2012, 9(4): 428-432. DOI: 10.3969/j.issn.1672-7940.2012.04.011 |
| [16] |
张军华, 缪彦舒, 郑旭刚, 等. 预测反褶积去多次波几个理论问题探讨[J].
物探化探计算技术, 2009, 31(1): 6-10.
ZHANG Junhua, MIAO Yanshu, ZHENG Xugang, et al. Discussion of several theoretical questions to remove seismic multiples using predictive deconvolution[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2009, 31(1): 6-10. DOI: 10.3969/j.issn.1001-1749.2009.01.003 |
 2017, Vol. 49
2017, Vol. 49


