2. 金属矿山高效开采与安全教育部重点实验室(北京科技大学),北京 100083
2. Key Laboratory of High-Efficient Mining and Safety of Metal Mines(University of Science and Technology Beijing), Ministry of Education, Beijing 100083, China
地应力在地下岩体工程建设中具有举足轻重的作用[1].了解工程地区的地应力分布特征,可以确定工程岩体属性,进行围岩稳定性分析与支护结构设计,有利于实现岩土工程开挖设计和决策的科学化[2].此外,地应力状态也与断裂构造滑动失稳及地震孕育等密切相关.地应力场是一个相对稳定的非稳定应力场,虽然地应力场是复杂多变的,在各个区域也不尽相同,但其随深度的分布仍表现出一定的规律性,这一点从国内外学者根据实测地应力数据得到的地壳浅层地应力分布规律也可以看出[3-5].目前国内外已发展和应用的地应力测量方法主要有扁千斤顶法、水压致裂法、刚性圆筒应力计、声发射法、应力解除法、应变恢复法、钻孔崩落法、地球物理探测法及地质方法等[1].其中水压致裂法与应力解除法的技术设备成熟,测量精度较高,广泛应用于各类工程.地应力测量面临岩体介质差异性、节理裂隙、地下水、温度等各种因素的影响,各类测量方法的适用性、操作性,尤其是复杂地质条件下的测量精度,有待进一步细化研究和改善.
21世纪是“地下空间”的世纪.近年来,国内外各类地下工程都在逐步向深部延伸,不断刷新着深度记录.以金属矿山行业为例,南非绝大多数金矿的开采深度大都在2 000 m以下,目前最深的Western Deep Level金矿的开采深度已经达到4 700 m[6].中国金属矿山的开采深度也在不断深入,其中云南会泽铅锌矿、吉林夹皮沟金矿和辽宁红透山铜矿的开采深度分别达到了1 500、1 400、1 300 m[7].浅部和深部岩体的赋存环境差异很大,深部岩体处于构造应力场与残余构造应力场双重作用环境中,两种应力场综合叠加为高应力,在深部岩体中形成了异常的地应力场.根据谢和平等[8]对世界30多个国家的地应力分布图分析可知,浅部的地应力状态以构造应力为主,随深度的增加,深部的地应力状态逐渐变为静水压力状态,这是深部与浅部岩体应力状态的显著区别.本文根据收集到的中国大量实测地应力资料,首次对划分的浅部和深部工程区的地应力分布特征分别进行统计分析,并对二者进行具体比较;然后依据库仑滑动摩擦准则,探讨浅部和深部在现今应力状态下的断裂稳定性及判断断裂滑动失稳的摩擦系数取值标准.
1 实测地应力数据资料在收集数据时,本文参考何满潮等[9]关于浅部工程与深部工程的界定方法,将深度在500 m以上的范围定为浅部工程区,深度超过500 m的范围定为深部工程区.本文地应力数据资料来源广泛,既有《世界地应力实测资料汇编》[10]和《中国大陆地壳应力环境研究》[11]中的地应力数据,又收集了国内多个煤矿、金属矿山、隧洞洞库、铁路隧道、水(核)电站及中国大陆科学钻探主钻孔等工程的实测地应力数据.此外,还收集了国内近两年发表的文献中有关中国最近建设的重大水电、交通、高放废物处置等领域深埋地下工程现场实测地应力数据,如双江口水电站、当金山隧道、高放废物地质处置库北山预选区等.地应力数据分布地点基本覆盖了中国大陆地区,具有广泛的代表性.
为了保证所得结论的可靠性,在分析之前,首先对地应力数据进行优化处理,具体处理方法见文献[12].由于浅部数据分布较离散,深部数据分布较密集,因而仅对浅部数据进行筛选处理,处理方法见图 1.最后共剩下有效实测地应力数据995组,其中浅部数据有376组,深度H最浅11 m,最深498 m;深部数据有619组,深度最浅502 m,最深5 047 m.所采用的995组地应力数据大部分是由水压致裂法和应力解除法测得的,还有少量的钻孔崩落法测量数据.
|
图 1 浅部σH、σh和σv数据优化处理示意图 Figure 1 Data optimization of σH, σh, and σv of shallow rocks |
经统计得,浅部有194组数据3个主应力关系为σH>σh>σv,约占51.60%,根据Anderson断层理论,属逆断型应力结构,有利于逆断层的发育活动,如陕西汉中盆地及周边地区测量钻孔附近存在有大量逆断层和挤压褶皱,该地测得的3个主应力关系恰为σH>σh>σv[13];有182组数据3个主应力之间的关系为σH>σv>σh,约占48.40%,属走滑型应力结构,有利于走滑断层的发育活动,如冀东地区马城附近深县—乐亭断裂第四纪具有左旋正断的活动特性,该地GK1-2钻孔测得3个主应力的关系为σH>σv>σh[14].在深部,183组数据的3个主应力关系为σH>σh>σv,约占29.56%;403组数据的3个主应力关系为σH>σv>σh,约占65.11%;33组数据的3个主应力关系为σv>σH>σh,约占5.33%,属正断型应力结构,该应力结构特征有利于正断层活动,如金州断裂带北段现今表现为正断层作用,该地所测得的3个主应力关系为σv>σH>σh[15].分析可知,浅部以σH>σh>σv型、σH>σv>σh型应力结构为主,二者所占比重基本相当.深部σH>σv>σh型应力结构占绝对优势,也有少量以垂直主应力为主的情况.与浅部相比,深部逆断型应力结构比重下降,走滑型应力结构比重增加,且出现了正断型应力结构,表明深部地应力场有从构造应力场向垂直应力场转变的趋势.
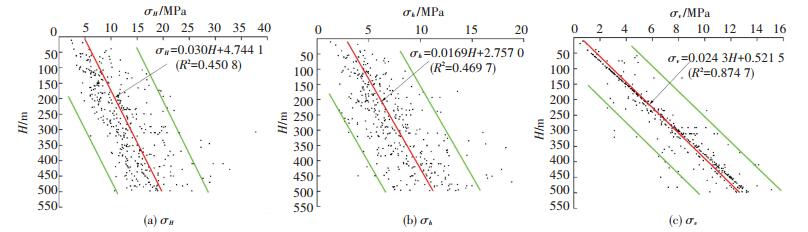
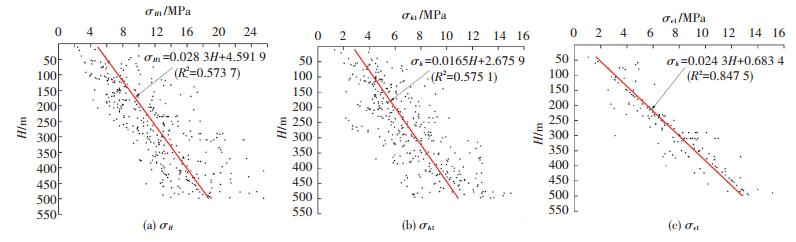
2.2 主应力随深度变化由于水压致裂数据和钻孔崩落数据中的垂直主应力是根据上覆岩层重量估算得到的,不是真实的垂直主应力,而应力解除法得到的是实际垂直主应力.因此,分析浅部和深部垂直主应力与深度关系时,只采用应力解除数据.国内外大量研究表明,地应力量值整体上随深度的增加而增大,近似成线性关系.目前普遍采用最小二乘法对3个主应力与深度的关系进行线性回归拟合,具有一定的合理性.浅部和深部的主应力随深度变化规律与线性回归方程如图 2、3所示,图中回归方程中各参数的意义为:σH1、σh1、σv1分别为浅部的最大水平主应力、最小水平主应力和垂直主应力,σH2、σh2、σv2分别为深部最大水平主应力、最小水平主应力和垂直主应力.
|
图 2 浅部σH1、σh1和σv1随深度变化曲线 Figure 2 σH1, σh1, and σv1 of shallow rocks variation with depth |

|
图 3 深部σH2、σh2和σv2随深度变化曲线 Figure 3 σH2, σh2, and σv2 of deep rocks variation with depth |
从图 2、3中可以看出,浅部和深部主应力随深度的变化规律整体上符合“主应力随深度呈线性增加”这一结论,但数据离散性也较大,尤其是浅部.根据回归方程,σH1、σh1的相关性系数R2只达到了0.57,线性关系不显著.而深部σH2、σh2的相关性系数R2超过了0.85,拟合精度较高,线性关系较好,表明深部的水平主应力的变化比浅部稳定.分析认为,浅部的地应力状态受地表风化剥蚀、沉积环境及地形地貌等因素的影响较大,导致浅部地应力场呈现出非均匀分布的特征.浅部σv1的相关性系数大于深部σv2的,这可能与深部σv2随深度分布的非连续性有关.
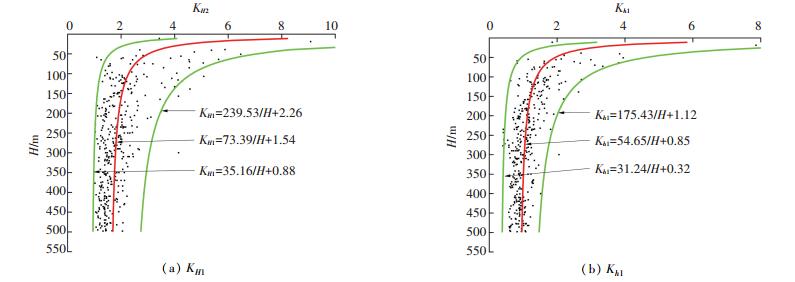
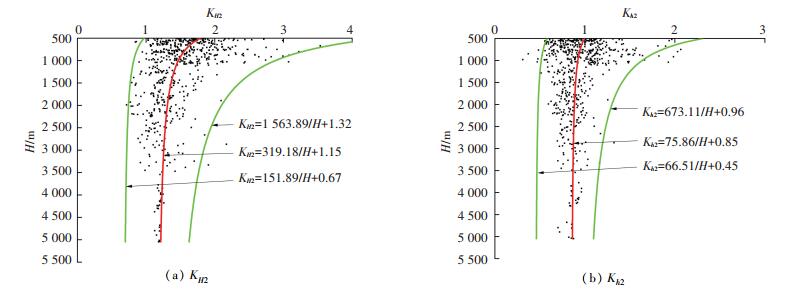
2.3 侧压系数随深度变化最大与最小水平主应力的平均值与垂直主应力的比值常用来描述地下某点的应力状态和地应力随深度的变化规律.本文采用最大水平主应力与垂直主应力之比KH和最小水平主应力与垂直主应力之比Kh这两个指标(统称为侧压系数)来研究浅部和深部的地应力变化趋势,如图 4、5所示.其中KH1、Kh1分别为浅部对应的两个侧压系数,KH2、Kh2分别为深部对应的两个侧压系数.
|
图 4 浅部侧压系数KH1、Kh1随深度变化曲线 Figure 4 Lateral pressure coefficient KH1 and Kh1 of shallow rocks variation with depth |
|
图 5 深部侧压系数KH2、Kh2随深度变化曲线 Figure 5 Lateral pressure coefficient KH2 and Kh2 of deep rocks variation with depth |
统计得,在浅部,KH1=1.02~9.08;Kh1=0.41~7.86.在深部,KH2=0.72~3.54;Kh2=0.31~2.07.由图 4、5可知,浅部和深部各自的两个侧压系数整体上随着深度的增加而减小,符合已有的认识和规律.浅部的两个侧压系数值比深部的分布较离散,波动幅度较大,地应力在浅部的变化比较明显.到了深部,两个侧压系数值分布更集中,并随着深度的增加而快速收敛,逐渐趋向于一个恒定值,随深度的变化不再敏感.总体来看,KH1向1.54趋近,Kh1向0.85趋近;KH2趋向于1.15,Kh2趋向于0.85,这与世界30多个国家的地应力分布情况[8]基本一致.侧压系数的减小是非线性的,其变化趋势以双曲线的形式表示,但深部的侧压系数与深度的双曲线关系不如浅部显著,表明水平构造应力场在浅部岩体的主导作用要强于深部岩体.
2.4 水平差应力随深度变化水平差应力(最大与最小水平主应力的差值)与岩体中的剪应力密切相关,在一定程度上能反映工程岩体的稳定性,较高的差应力是影响地下工程围岩稳定的主导因素.对浅部和深部的水平差应力进行分析,有助于进一步认识水平构造应力场的变化趋势,也可为判断地下工程围岩的稳定程度提供一定参考.为便于叙述,本文用η来表示水平差应力,即η=σH-σh.由图 6可知,浅部η1和深部η2随深度分布比较散乱,波动范围比较大,整体上随深度增加有增大的趋势.水平差应力随深度增大,可能与岩石的弹性模量、强度随深度的增大有关.分析数据知,η1=0.10~16.91 MPa;η2=0.84~58.50 MPa.深部的水平差应力最大达到了58.50 MPa,这对深部工程的稳定性是极为不利的.浅部的岩体大多处于弹性应力状态,而深部岩体则可能处于塑性状态,水平差应力较大而引起的剪应力超过岩石强度时,容易造成不良结构面、岩石的变形破坏.深部较浅部所处的应力构造环境更容易在工程临空面形成高的差应力,这大大地增加了地下工程围岩支护的难度,同时也增加了岩爆等灾害发生的概率.

|
图 6 浅部η1、深部η2随深度变化曲线 Figure 6 η1 of shallow rocks and η2 of deep rocks variation with depth |
综上分析,浅部和深部地应力场特征表现出较大差异.与浅部相比,深部岩体应力状态发生了较大变化,所处的构造应力场更复杂.这不仅与浅部和深部在地形地貌、沉积环境及岩石风化程度等地质方面的差异有关,与板块构造运动也有很大关系.由于地应力场的差异,在进行浅部工程和深部工程建设时,应采用有针对性的施工工艺和支护技术.
3 浅部和深部断裂稳定性探讨 3.1 断裂摩擦滑动准则式(1) 为库仑摩擦滑动准则,常用于研究岩石的剪切破坏,在判定断裂滑动时,库仑摩擦滑动准则通常假定断裂面内聚力C=0,当断裂面上的剪应力τ满足τ≥μσn时,断裂面将沿某一角度发生滑动失稳. Jaeger等[16]认为,临界方向断裂处于摩擦极限时有效最大主应力与最小主应力之比满足式(2).
| $\tau =C+\mu {{\sigma }_{\rm{n}}},$ | (1) |
| $\frac{{{\sigma }_{1}}-{{P}_{0}}}{{{\sigma }_{3}}-{{P}_{0}}}={{\left( \sqrt{1+{{\mu }^{2}}}+\mu \right)}^{2}}.$ | (2) |
式中:τ为断裂面上的剪应力;C为断裂面内聚力;μ为断裂带滑动摩擦系数;σn为断裂面上的正应力;σ1、σ3分别为最大、最小主应力;P0为孔隙压力.
由前面数据分析可知,浅部的应力状态有利于发育逆断层和走滑断层,深部的应力状态有利于发育逆断层、走滑断层和正断层.根据Anderson断层理论可以确定不同类型的断层所在区域的构造应力特征,将式(2) 与Anderson断层理论结合,可以得到逆断层、走滑断层和正断层的应力特征,见式(3).若式(3) 中方程左边小于右边,则断层稳定,若左边大于或等于右边,断层将沿最优断面失稳滑动[17].
| $\left\{ \begin{align} &逆:\frac{{{\sigma }_{1}}-{{P}_{0}}}{{{\sigma }_{3}}-{{P}_{0}}}=\frac{{{\sigma }_{H}}-{{P}_{0}}}{{{\sigma }_{v}}-{{P}_{0}}}={{(\sqrt{1+{{\mu }^{2}}}+\mu )}^{2}}, \\ &走滑:\frac{{{\sigma }_{1}}-{{P}_{0}}}{{{\sigma }_{3}}-{{P}_{0}}}=\frac{{{\sigma }_{H}}-{{P}_{0}}}{{{\sigma }_{h}}-{{P}_{0}}}={{(\sqrt{1+{{\mu }^{2}}}+\mu )}^{2}}, \\ &正:\frac{{{\sigma }_{1}}-{{P}_{0}}}{{{\sigma }_{3}}-{{P}_{0}}}=\frac{{{\sigma }_{v}}-{{P}_{0}}}{{{\sigma }_{h}}-{{P}_{0}}}={{(\sqrt{1+{{\mu }^{2}}}+\mu )}^{2}}.~ \\ \end{align} \right.$ | (3) |
对于确定式(3) 中μ的大小,国内外学者也进行了大量的研究. Byerlee[18]分析各类岩石试验数据发现,应力值小于200 MPa时,大部分岩石的μ值为0.85,应力值大于200 MPa且小于2000 MPa时,岩石的μ值为0.6. Zoback等[19]分析6口深孔资料认为,地壳浅表层应力状态取μ为0.6~1.0是基本合适的.刘晓红等[20]用双剪法测量了中国6条断裂断层泥的摩擦系数,这6条断裂的摩擦系数在0.465~0.697之间,平均为0.547.秦向辉等[21]在评价北京地区主要断裂稳定性时,考虑了断裂带摩擦系数的弱化,选取摩擦系数为0.2~1.0.以往常用μ=0.6和1.0作为判断断层失稳时的下限值和上限值,然而有学者指出,实际条件下断裂带的摩擦系数可能要低一些,有些稳态摩擦系数为0.2~0.22[22].综合以上分析,本文选取μ值为0.2、0.4、0.6和1.0,以实测地应力数据为基础,对浅部和深部的断裂稳定性进行较全面地探讨.
3.2 断裂稳定性判断由于深部正断型应力结构所占比例很少,限于篇幅,不再对其详述,主要对浅部和深部的逆断型应力结构、走滑型应力结构进行分析.将μ的4个值0.2、0.4、0.6和1.0分别代入式(3) 计算得:μ=0.2时,σH-P0=1.49(σv-P0)(逆断层),σH-P0=1.49(σh-P0)(走滑断层);μ=0.4时,σH-P0=2.18(σv-P0)(逆断层),σH-P0=2.18(σh-P0)(走滑断层);μ=0.6时,σH-P0=3.12(σv-P0)(逆断层),σH-P0=3.12(σh-P0)(走滑断层);μ=1.0时,σH-P0=5.83(σv-P0)(逆断层),σH-P0=5.83(σh-P0)(走滑断层).计算结果见图 7.
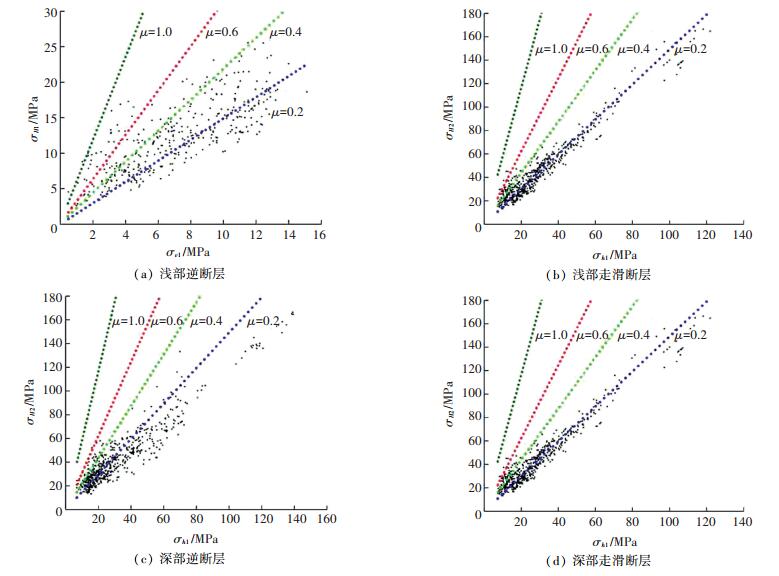
|
图 7 浅部逆断层、走滑断层和深部逆断层、走滑断层稳定性评价结果 Figure 7 Assessment results of stability of thrust and strike-slip fault of shallow rocks, and thrust and strike-slip fault of deep rocks |
由图 7(a)、7(b)可以看出,在浅部,μ取1.0时,应力状态尚未达到走滑断层滑动失稳所需要的水平,不会发生瞬间滑动,处于相对稳定状态;有极少数数据超过了逆断层滑动失稳临界水平,这一现象值得进一步关注,但整体处于相对稳定状态. μ取0.6时,有大量数据超过了逆断层滑动的临界区,有滑动的可能,对于走滑断层,有个别数据超过了其滑动失稳界限,整体上处于相对稳定状态.当μ弱化到0.4、0.2时,地应力状态达到滑动失稳的要求,两类断层均有滑动的危险. 图 7(c)、7(d)表明,在深部,μ取1.0时,两类断层不具有滑动失稳的危险性. μ取0.6时,仅有极少量数据达到了断裂滑动失稳条件,两类断层发生滑动失稳的可能性很小. μ弱化到0.4时,有部分数据超过了断裂滑动失稳的界值,两类断层有发生滑动失稳的可能.当两类断层μ弱化到0.2,有大量数据超过了断裂滑动失稳的限值,两类断层发生滑动的危险性显著增加.
分析认为,浅部和深部断裂一般难以承受μ取1.0时那么大的应力值,浅部断裂滑动失稳标准取摩擦系数为0.6~1.0较为合适,深部断裂滑动失稳标准取摩擦系数为0.4~0.6比较合理. μ值的选取,也再一次证明了浅部3个主应力值相差较大,深部3个主应力值比较接近.可以推测,深部比浅部断裂处于相对稳定的状态,这可能是因为浅部应力状态一定程度上受地形和局部构造的影响造成应力波动范围比较大,而深部应力状态相对均匀.在浅部地下工程遇到断裂时,需对断裂的稳定性及时进行评估并采取相应处理措施,以免发生灾害.若从断层类型角度来选取μ值大小,逆断层滑动失稳标准可以取μ值为0.6左右,对于走滑断层,滑动失稳标准可以取μ值为0.4左右,这对今后判断不同类型断裂的滑动失稳具有一定参考价值.另外,有研究认为[23],可以根据断裂发生滑动失稳的条件估算更深处(几十千米深度)的应力范围,依靠估算结果推测更深处断层的稳定性,为分析地震的发生条件提供一定帮助.需要指出的是,上述分析中未考虑孔隙压力的影响,一定程度上简化了断裂滑动失稳判据.
4 结论1) 浅部以逆断型和走滑型应力结构为主,二者所占比重相当.深部有3种应力结构:逆断型、走滑型和正断型,其中走滑型应力结构占绝对优势,也有少量以垂直主应力为主的情况.
2) 浅部σH1、σh1、σv1的应力变化梯度分别为0.028 3、0.016 5、0.024 3,深部σH2、σh2、σv2的应力变化梯度分别为0.026 5、0.019 9、0.025 0.深部和浅部对应的3个侧压系数值随着深度的增加逐渐趋向于一个恒定值,KH1、Kh1分别向1.54、0.85趋近;KH2、Kh2分别趋向于1.15、0.85.浅部η1为0.10~16.91 MPa,深部η2为0.84~58.50MPa,η1、η2整体上随深度增加有增大的趋势.
3) μ取1.0时,浅部和深部断裂带基本处于相对稳定状态. μ取0.6时,浅部逆断层有较大的滑动可能,深部断裂滑动失稳的可能性较小.当μ弱化到0.4、0.2时,浅部和深部的断裂带发生滑动失稳的可能性显著增加.浅部断裂滑动失稳标准取μ为0.6~1.0较为合适,深部断裂滑动失稳标准取μ为0.4~0.6比较合理.逆断层、走滑断层的滑动失稳标准可分别取μ值为0.6、0.4左右.
| [1] |
蔡美峰.
地应力测量原理和技术[M]. 北京: 科学出版社, 2000.
|
| [2] |
蔡美峰, 王双红. 地应力状态与围岩性质的关系研究[J].
中国矿业, 1997, 6(6): 38-41.
CAI Meifeng, WANG Shuanghong. Relation between ground stress behavior and properties of surrounding rock[J]. China Mining Ma-gazine, 1997, 6(6): 38-41. |
| [3] |
WOROTNIKI G, DENHAM D. The state stress in the upper part of the Earth's crust in Australia according to measurements in tunnels and mines and from seismic observation[C]// Investigation of Stress in Rock-Advances in Stress Measurement, Int Soc Rock Mech. Symp, Sydney: Institution of Engineers, Australia, 1976: 71-82.
|
| [4] |
BROWN E T, HOEK E. Technical note trends in relationships between measured in-situ stress and depth[J].
International Journal of Rock Mechanics and Mining Sciences andGeomechanics Abstracts, 1978, 15(4): 211-215.
DOI: 10.1016/0148-9062(78)91227-5 |
| [5] |
杨树新, 姚瑞, 崔效锋, 等. 中国大陆与各活动地块、南北地震带实测应力特征分析[J].
地球物理学报, 2012, 55(12): 4207-4217.
YANG Shuxin, YAO Rui, CUI Xiaofeng, et al. Analysis of the characteristics of measured stress in Chinese mainland and its active blocks and North-South seismic belt[J]. Chinese Journal of Geophysics, 2012, 55(12): 4207-4217. DOI: 10.6038/j.issn.0001-5733.2012.12.032 |
| [6] |
DIERING D H. Ultra-deep level mining: future requirements[J].
Journal of the South African Institute of Mining and Metallurgy, 1997, 97(6): 249-255.
|
| [7] |
CAI M F. Prediction and prevention of rockburst in metal mines—a case study of Sanshandao gold mine[J].
Journal of Rock Mechanics and Geotechnical Engineering, 2016, 8(2): 204-211.
DOI: 10.1016/j.jrmge.2015.11.002 |
| [8] |
谢和平, 高峰, 鞠杨, 等. 深部开采的定量界定与分析[J].
煤炭学报, 2015, 40(1): 1-10.
XIE Heping, GAO Feng, JU Yang, et al. Quantitative definition and investigation of deep mining[J]. Journal of China Coal Society, 2015, 40(1): 1-10. DOI: 10.13225/j.cnki.jccs.2014.1690 |
| [9] |
何满潮, 吕晓俭, 景海河. 深部工程围岩特性及非线性动态力学设计理念[J].
岩石力学与工程学报, 2002, 21(8): 1215-1224.
HE Manchao, LU Xiaojian, JING Haihe. The characteristics of the rock mass in deep engineering and the design concept of nonlinear dynamic mechanics[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(8): 1215-1224. |
| [10] |
陈彭年, 陈宏德, 高莉青.
世界地应力实测资料汇编[M]. 北京: 地震出版社, 1990.
|
| [11] |
谢富仁, 陈群策, 崔效锋, 等.
中国大陆地壳应力环境研究[M]. 北京: 地质出版社, 2003.
|
| [12] |
李鹏, 苗胜军. 中国煤矿矿区地应力场特征与断层活动性分析[J].
煤炭学报, 2016, 41(Sup2): 319-329.
LI Peng, MIAO Shengjun. Analysis of the characteristics of in-situ stress field and fault activity in the coal mining area of China[J]. Journal of China Coal Society, 2016, 41(Sup2): 319-329. DOI: 10.13225/j.cnki.jccs.2016.0303 |
| [13] |
杜建军, 陈群策, 安其美, 等. 陕西汉中盆地水压致裂地应力测量分析研究[J].
地震学报, 2013, 35(6): 799-808.
DU Jianjun, CHEN Qunce, AN Qimei, et al. Hydrofracturing in-situ stress measurement in Hanzhong Basin, Shaanxi Province[J]. Acta Seismologic Sinica, 2013, 35(6): 799-808. |
| [14] |
牛琳琳, 杜建军, 丰成君, 等. 冀东地区深孔地应力测量及其意义[J].
地震学报, 2015, 37(1): 89-102.
NIU Linlin, DU Jianjun, FENG Chengjun, et al. In-situ stress measurement of deep borehole in east of Hebei and its significance[J]. Acta Seismologic Sinica, 2015, 37(1): 89-102. DOI: 10.11939/jass.2015.01.008 |
| [15] |
张鹏, 丰成君, 孙炜峰, 等. 金州断裂带北段深孔地应力测量及其活动性[J].
地球科学, 2014, 39(10): 1395-1406.
ZHANG Peng, FENG Chengjun, SUN Weifeng, et al. In-situ stress measurement of deep borehole in north segment of Jinzhou fracture belt and analysis on its activity[J]. Earth Science, 2014, 39(10): 1395-1406. DOI: 10.3799/dqkx.2014.122 |
| [16] |
JAEGER J C, COOK N G W.
Fundamentals of Rock Mechanics2nd ed[M]. New York: Chapman & Hall, 1979.
|
| [17] |
李鹏, 苗胜军. 中国大陆金属矿区实测地应力分析及应用[J].
工程科学学报, 2017, 39(3): 323-334.
LI Peng, MIAO Shengjun. Analysis and application of in-situ stress in metal mining area of Chinese mainland[J]. Chinese Journal of Engineering, 2017, 39(3): 323-334. DOI: 10.13374/j.issn2095-9389.2017.03.002 |
| [18] |
BYERLEE J D. Friction of rocks[J].
Pure Appl Geophys, 1978, 116: 615-626.
DOI: 10.1007/BF00876528 |
| [19] |
ZOBACK M D, TOWNEND J. Implications of the hydrostatic pore pressures and high crustal strength for the deformation of intraplate lithosphere[J].
Tectonophysics, 2001, 336(1): 19-30.
|
| [20] |
丰成君, 陈群策, 李国歧, 等. 青藏高原东南缘丽江—剑川地区地应力测量与地震危险性[J].
地质通报, 2014, 33(4): 524-534.
FENG Chengjun, CHEN Qunce, LI Guoqi, et al. In-situ stress measurement in Lijiang-Jianchuan area and tentative discussion on the seismic hazards on the southeastern margin of the Tibetan Plateau[J]. Geological Bulletin of China, 2014, 33(4): 524-534. |
| [21] |
秦向辉, 张鹏, 丰成君, 等. 北京地区地应力测量与主要断裂稳定性分析[J].
地球物理学报, 2014, 57(7): 2165-2180.
QIN Xianghui, ZHANG Peng, FENG Chengjun, et al. In-situ stress measurements and slip stability of major faults in Beijing region, China[J]. Chinese Journal of Geophysics, 2014, 57(7): 2165-2180. DOI: 10.6038/cjg20140712 |
| [22] |
ZHANG L, HE C R. Frictional properties of natural gouges from Longmenshan fault zone ruptured during the Wenchuan Mw7.9 earthquake[J].
Tectonophysics, 2013, 594(5): 149-164.
DOI: 10.1016/j.tecto.2013.03.030 |
| [23] |
曹辉, 孙东生, 孟文, 等. 安第斯山中段现今地应力测量及地震相关性分析[J].
地球学报, 2015, 36(2): 250-254.
CAO Hui, SUN Dongsheng, MENG Wen, et al. In-situ stress mea-surement in the central section of Andes and its relation to seismicity[J]. Acta Geoscientica Sinica, 2015, 36(2): 250-254. DOI: 10.3975/cagsb.2015.02.15 |
 2017, Vol. 49
2017, Vol. 49


