为满足居民出行和群体活动的需求,城市交通枢纽、体育场馆等各类行人步行设施的建设规模不断增加.步行设施物理空间是集散行人流路径选择和集散时间等各种群体宏观现象与特征的形成基础.步行设施空间布局的合理性严重影响正常或紧急集散过程中行人的集散时间、拥挤程度、移动距离,以及设施的集散能力和安全性等.为提高行人疏散效率、缩短疏散移动距离和时间、缓解行人流拥堵、避免踩踏事件发生等,需要从设施建设阶段,分析步行设施的空间疏散特征,形成合理的空间布局.因此,行人步行设施空间疏散特征研究是建筑设施消防、交通枢纽设计等公共安全领域研究的热点.
在步行设施内行人组织管理研究领域,主要包括疏散诱导标志设置、行人疏散路径或安全出口选择、步行设施的疏散设计和评价、设施内行人疏散仿真、设施内行人流特征分析等相关研究;采用经验分析、疏散实验、模拟仿真、现场调查等方法,分析研究步行设施空间布局既定方案下疏散诱导标志的布局优化[1]、设置方法[2]、行人疏散路径选择[3],安全出口设置[4],行人安全出口的选择行为[5-6],紧急情况下行人疏散路径选择行为[7],步行疏散过程中的空间时间利用有效性[8],大型行人步行设施的疏散设计[9-10],行人疏散过程的模拟再现[11-13],步行设施内行人流微观与宏观行为特征分析[14]等.
目前研究着重于步行设施既定设计方案下的疏散仿真与评价,而对行人步行设施疏散特性下的空间特征分析研究相对较少.本文为实现步行设施内物理空间的合理布局,对步行设施内物理空间布局进行疏散特征指标分析.将步行设施的物理空间抽象为移动网络,基于移动网络和移动距离最短的疏散路径选择策略,将移动网络转化为疏散树,并基于疏散树层与节点的隶属关系,以及行人疏散流的移动特征,分析步行设施的空间疏散特征指标.
1 步行设施空间网络化步行设施内空间主要分两大类:一为可被行人占据供行人实现空间位移的移动空间,如步行通道、走廊、楼梯等行人移动区域;二为不能用于行人实现空间位移的障碍物空间,如行人禁行区、立柱、墙、隔栏等辅助设施占据的区域.
1.1 行人疏散瓶颈行人移动的瓶颈是障碍物空间对移动空间的挤压,导致行人移动空间发生形变.瓶颈宽度用毗邻障碍物边缘之间的最短直线距离表示,如图 1(a)所示.因此,可知步行设施的安全出口属于瓶颈.瓶颈是空间布局的固有属性,不受步行空间内行人数量与移动方向的影响.当行人理想移动方向与瓶颈断面不相垂直时,拥堵行人流的自组织行为将会最大限度地利用瓶颈宽度,如图 1(b)所示.瓶颈的行人通过能力与其宽度密切相关.为便于计算瓶颈宽度,将障碍物空间外缘轮廓线简化为弧线和线段,相邻障碍物外缘轮廓线之间的最短距离为瓶颈的宽度,如图 1所示.
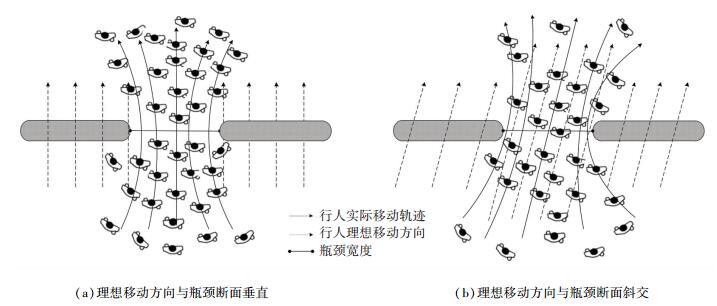
|
图 1 行人步行设施移动瓶颈示意图 Figure 1 The illustration of movement bottleneck in pedestrian walking facilities |
步行设施移动空间被瓶颈分割为不同的局部移动区域,各局部移动区域通过瓶颈拼接为步行设施的整体移动空间.行人经瓶颈实现在不同局部移动区域之间的移动.为了便于分析,步行设施内外区域均可被看作移动空间,设施围墙和设施内障碍物均被视为障碍物空间,如图 2(a)所示.为描述步行设施的空间布局以及局部移动区域的毗邻情况,将步行设施抽象为以局部移动区域为节点,瓶颈为弧的移动网络.当某一局部移动区域内行人由于行人组织方案或移动距离的影响选择不同的移动方向或路线疏散时,可以人为地分割局部移动区域,使分割后的每个子节点内的行人具有相同的疏散路线,如图 2所示.
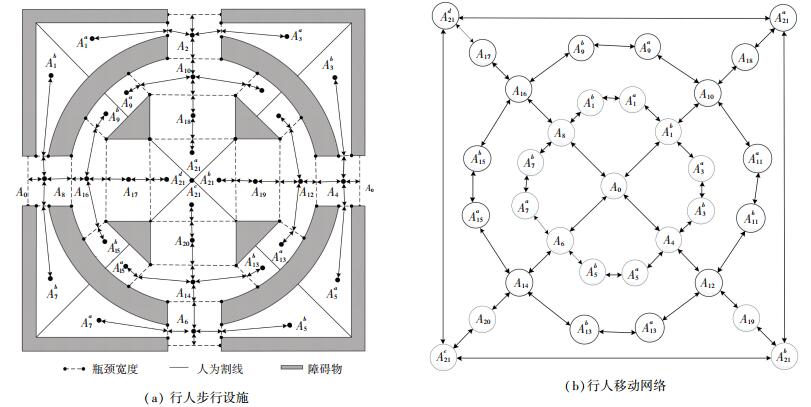
|
图 2 行人步行设施空间与移动网络示意图 Figure 2 The illustration of pedestrian facilities and movement network |
移动网络由两部分组成:节点和双向弧.节点包括行人流发生节点、中间节点、吸引节点;双向弧代表毗邻节点之间的瓶颈.步行设施转换为多起点单讫点(MOSD)的移动网络如图 2(b)所示. 图 2中,A0~A21为设施内局部移动区域或行人移动网络节点编号.当两个局部移动区域是由人为分割形成时,采用上角标的形式加以区分,如区域节点A15a和A15b;同时,A0为吸引节点,代表行人移动的目的地,即步行设施外的安全区域.
基于设施空间布局和最短路的疏散策略,可将MOSD移动网络转化为以讫点为根节点,起点为叶节点的疏散树.由图 2所示的移动网络转换为的疏散树如图 3所示.
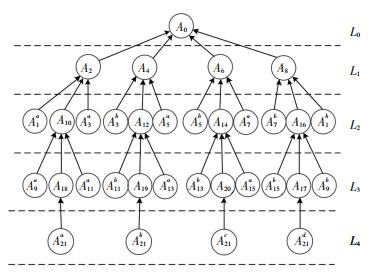
|
图 3 基于MOSD移动网络的疏散树示意图 Figure 3 The evacuation tree of pedestrian facilities based on MOSD network |
定义疏散树中根节点为第0层,与其毗邻的节点为第1层,依次类推分别为第2,3,……层,如图 3所示;同时,定义所有拥有相同层次编号j的节点集合为疏散树的疏散层Lj,疏散层编号即为节点层编号.行人疏散是从大编号向小编号的疏散层逐步移动的过程,当某A节点或层内的行人必须途径另一个B节点或层才能离开步行设施空间时,称A节点或层隶属于B节点或层.定义隶属于节点i的所有节点为节点i的隶属集合,记作Ni;隶属于层j的所有节点为层j的隶属集合,记作Mj;在Ni内,与节点i直接毗邻的节点集合定义为i的直接隶属集合NiT.由节点与层的隶属集合关系可知,层j的隶属集合是该层内所有节点隶属集合的并集.
2 步行设施空间疏散特征指标在行人步行设施空间设计过程中,影响行人疏散的主要因素包括行人数量、移动距离、瓶颈宽度、障碍物布局不平衡系数等.在实际的工程应用中,步行设施移动空间的总面积决定了可容纳的行人数量;移动距离决定了行人到达安全出口的步行距离;疏散瓶颈对群体行人疏散的阻滞作用,导致行人在瓶颈处形成拥挤排队,增加行人疏散时间.障碍物布局不平衡系数[13]主要描述行人疏散空间面积与疏散瓶颈的匹配协调性,反映行人疏散过程中局部严重拥堵对疏散过程的影响.因此,为确保行人的安全疏散,从空间面积、移动距离、瓶颈宽度、障碍物布局不平衡系数4个方面,分别从节点与疏散层的角度分析步行设施的空间疏散特征指标.
2.1 行人疏散空间面积行人疏散空间面积包括节点与层的疏散空间面积,是其隶属集合内节点的面积之和,描述该节点或层在疏散过程中所承担的疏散面积.节点i与层j的疏散空间面积Snode(i)与Slayer(j)分别为
| ${S_{{\rm{node}}}}\left( i \right) = \sum\limits_{k \in {N_i}} {{S_k}} ,$ | (1) |
| ${S_{{\rm{layer}}}}\left( j \right) = \sum\limits_{k \in {M_i}} {{S_k}} .$ | (2) |
式中:Sk为节点k的面积.由疏散树及其节点隶属关系可知,Snode(0)=Slayer(0);同时,可通过个体行人的空间需求面积大体推导出步行设施内各局部移动域区所能承担的最大行人数量.
2.2 行人疏散移动距离从节点的角度,行人疏散移动距离包括Ni内所有节点到节点i的最大距离Dnodemax(i)、平均距离Dnodeavg(i)、加权距离Dnodewgh(i),分别描述隶属集合内的行人到节点i的最远距离、低密度情况下的平均移动距离、高密度情况下的加权移动距离.分别表示为
| $D_{{\rm{node}}}^{\max }\left( i \right) = \mathop {\max }\limits_{k \in {N_i}} \left( {{d_{ki}}} \right),$ | (3) |
| $D_{{\rm{node}}}^{{\rm{avg}}}\left( i \right) = \frac{1}{n}\sum\limits_{k \in {N_i}} {{d_{ki}}} ,$ | (4) |
| $D_{{\rm{node}}}^{{\rm{wgh}}}\left( i \right) = \sum\limits_{k \in {N_i}} {\frac{{{s_k}}}{{{S_{{\rm{node}}}}\left( i \right)}}{d_{ki}}} .$ | (5) |
式中:n为Ni中节点数量;dki为疏散树中节点k到i的距离.
从层的角度,行人疏散移动距离包括隶属集合Mj内所有节点到层j的最大距离Dlayermax(j)、平均距离Dlayeravg(j)、加权距离Dlayerwgh(j).分别表示为
| $D_{{\rm{layer}}}^{\max }\left( j \right) = \mathop {\max }\limits_{k \in {M_j},r \in {L_j}} \left\{ {{d_{kr}}} \right\},$ | (6) |
| $D_{{\rm{layer}}}^{{\rm{avg}}}\left( j \right) = \frac{1}{m}\sum\limits_{k \in {M_j}} {\sum\limits_{r \in {L_j}} {{d_{kr}}} } ,$ | (7) |
| $D_{{\rm{layer}}}^{{\rm{wgh}}}\left( j \right) = \sum\limits_{k \in {M_j}} {\sum\limits_{r \in {L_j}} {\frac{{{s_k}}}{{{S_{{\rm{layer}}}}\left( j \right)}}{d_{kr}}} } .$ | (8) |
式中:m为集合Mj中节点的个数,dkr为疏散树中节点k到r的距离.
2.3 行人疏散瓶颈宽度从节点的角度,行人疏散瓶颈宽度包括直接隶属集合NiT内的节点到节点i的总宽度Wnodeall(i)、平均宽度Wnodeavg(i)、加权宽度Wnodewgh(i),分别描述进入节点的行人瓶颈总宽度、低密度情况下行人平均瓶颈宽度、高密度情况下行人加权瓶颈宽度.分别表示为
| $W_{{\rm{node}}}^{{\rm{all}}}\left( i \right) = \sum\limits_{k \in N_i^T} {{w_{ki}}} ,$ | (9) |
| $W_{{\rm{node}}}^{{\rm{avg}}}\left( i \right) = \frac{1}{n}\sum\limits_{k \in N_i^T} {{w_{ki}}} ,$ | (10) |
| $W_{{\rm{node}}}^{{\rm{wgh}}}\left( i \right) = \sum\limits_{k \in N_i^T} {\frac{{{s_k} + {S_{{\rm{node}}}}\left( k \right)}}{{{S_{{\rm{node}}}}\left( i \right)}}{w_{ki}}} .$ | (11) |
式中:n为集合NiT中节点的个数,wki表示节点k到节点i瓶颈的宽度.
从层的角度,行人疏散瓶颈宽度包括层j内节点与毗邻的层j-1内节点间的总宽度Wlayerall(j)、平均宽度Wlayeravg(j)、加权宽度Wlayerwgh(j)分别为
| $W_{{\rm{layer}}}^{{\rm{all}}}\left( j \right) = \sum\limits_{k \in {L_{j + 1}}} {\sum\limits_{r \in {L_j}} {{w_{kr}}} } ,$ | (12) |
| $W_{{\rm{layer}}}^{{\rm{avg}}}\left( j \right) = \frac{1}{m}\sum\limits_{k \in {L_{j + 1}}} {\sum\limits_{r \in {L_j}} {{w_{kr}}} } ,$ | (13) |
| $W_{{\rm{layer}}}^{{\rm{wgh}}}\left( j \right) = \sum\limits_{k \in {L_{j + 1}}} {\sum\limits_{r \in {L_j}} {\frac{{{s_k} + {S_{{\rm{node}}}}\left( k \right)}}{{{S_{{\rm{layer}}}}\left( j \right)}}{w_{kr}}} } .$ | (14) |
式中:m为层j与层j+1间的瓶颈个数.
2.4 障碍物布局不平衡系数从节点的角度,障碍物布局不平衡系数描述疏散树中节点i分担行人疏散数量的实际分担率与理想分担率的差异程度[13].理想分担率用Ni内节点的面积之比表示;实际分担率用NiT的移动瓶颈之比表示,节点i周边的障碍物布局不平衡系数βnode(i)为
| ${\beta _{{\rm{node}}}}\left( i \right) = \frac{{\sum\limits_{k \in N_i^T} {\left| {{\varphi _k} - {\phi _k}} \right|} }}{2},$ | (15) |
| ${\varphi _k} = \frac{{{s_k} + {S_{{\rm{node}}}}\left( k \right)}}{{{S_{{\rm{node}}}}\left( i \right)}},$ | (16) |
| ${\phi _k} = \frac{{{w_{ki}}}}{{W_{{\rm{node}}}^{{\rm{all}}}\left( i \right)}},$ | (17) |
| $\sum\limits_{k \in N_i^T} {{\varphi _k}} = \sum\limits_{k \in N_i^T} {{\phi _k}} = 1.$ | (18) |
式中:φk为节点k的理想分担率、ϕk为节点k的实际分担率,βnode(i)的取值在0~1之间,当βnode(i)=0时,节点i周边的障碍物布局是平衡的;当βnode(i)>0时,节点i周边的障碍物布局是不平衡的;随着βnode(i)的增加,障碍物布局的不平衡性增强.
从层的角度,障碍物布局不平衡系数描述疏散树中层j分担疏散行人数量的实际分担率与理想分担率的差异程度.层j周边的障碍物布局不平衡系数βlayer(j)为
| ${\beta _{{\rm{layer}}}}\left( j \right) = \frac{{\sum\limits_{k \in {L_{j + 1}}} {\left| {{\varphi _k} - {\phi _k}} \right|} }}{2};$ | (19) |
| ${\varphi _k} = \frac{{{s_k} + {S_{{\rm{node}}}}\left( k \right)}}{{{S_{{\rm{layer}}}}\left( j \right)}};$ | (20) |
| ${\phi _k} = \frac{{{w_{kr}}}}{{W_{{\rm{layer}}}^{{\rm{all}}}\left( j \right)}},r \in {L_j};$ | (21) |
| $\sum\limits_{k \in {L_{j + 1}}} {{\varphi _k}} = \sum\limits_{k \in {L_{j + 1}}} {{\phi _k}} = 1.$ | (22) |
同理,min βnode(i)的取值在0~1之间,当βlayer(j)=0时,层j周边的障碍物布局是平衡的;当βlayer(j)>0时,层j周边的障碍物布局是不平衡的;随着βlayer(j)的增加,障碍物布局的不平衡性增强.
3 步行设施空间布局的调整在步行设施空间布局调整过程中,首先,根据步行设施的类型、建筑物耐火等级、设计规范等,计算相关指标取值的合理范围;然后,根据步行设施的实际情况,分别计算4项指标;最后,筛选不合理指标,分析产生原因,并在符合工程需求的基础上,对其进行调整.
3.1 指标的合理取值理论方面,一个布局合理的步行设施在宏观与微观层面其布局都应该是合理的.首先,确保整个步行设施所容纳的行人数量在一个合理的范围内,即低密度与高密度情况下,须分别确保行人疏散瓶颈宽度保持在一定的合理范围内;其次,为避免局部移动区域发生严重拥堵或移动瓶颈过宽浪费的现象,每层或节点的障碍物不平衡系数要等于0.
每项指标的合理取值为:1) 疏散空间面积.疏散空间面积是反应步行设施容纳行人数量的指标.参考英国对公共建筑设施人群密度安全极限的规定,行进的人群密度为4人/m2,站立的静止人群密度为4.7人/m2[15].从而确定步行设施理想的行人疏散面积.可作为评价公共建筑疏散面积是否合理的标准. 2) 疏散移动距离.参照建筑设计防火规范[16](以下简称规范),公共建筑内,位于走廊尽头的房间,房间内任一点至疏散门的直线距离不大于15 m.规范中明确剧场、电影院、礼堂等公共建筑疏散时间,若建筑物耐火等级为一、二级,则疏散时间不大于2 min;若耐火等级为三级,则疏散时间不大于1.5 min.取行人平均速度1.34 m/s[17],则一、二级耐火等级的建筑内最大疏散距离不得大于160.8 m,三级耐火等级建筑最大疏散距离不得大于120.6 m,该距离是指行人从所在位置到安全出口的路径值.根据规范,由于体育馆内人数变化幅度较大,人员疏散时间依据不同容量按3~4 min控制,则最大疏散距离不得大于321.6 m.该距离可作为评价体育馆疏散移动距离指标合理与否的判断标准. 3) 疏散瓶颈宽度.参照规范,公共建筑内行人疏散过程中,移动瓶颈以0.55 m为一单位,对应的行人通过能力约40人/min.结合公共建筑允许的最长疏散时间、公共建筑设施人群密度安全值,可以确定一单位的移动瓶颈对应的疏散面积大小.以一、二等级耐火结构的剧场、电影院、礼堂、体育馆等公共建筑为例,安全疏散时间为2 min,则移动瓶颈为0.55 m时对应的疏散面积为40(人/min)☞2 min÷4(人/m2)=20 m2.同理三级耐火结构的公共建筑内,0.55 m的移动瓶颈承担的疏散面积是15 m2.结合上述表述,根据步行设施的耐火等级、步行设施类型等因素,可以确定一单位的移动瓶颈分担的合理疏散面积.该值可作为评价步行设施移动瓶颈合理与否的标准. 4) 障碍物布局不平衡系数.障碍物布局不平衡系数描述了疏散树中节点分担行人疏散数量的实际分担率与理想分担率的差异程度,实质上是反映了局部移动区域面积与瓶颈宽度匹配的合理程度,其取值在0~1之间.当布局不平衡系数等于0时,说明障碍物布局是平衡的,而且随着不平衡系数的增大,障碍物布局的不平衡性增强.
3.2 空间的布局调整在步行设施空间布局调整过程中,主要采用逐步调整与循环校核的方法,首先,调整层与层之间的布局关系,从宏观上保证每层各个指标合理;然后,对节点与节点间的局部不合理进行微调.具体调整流程如图 4所示.

|
图 4 基于疏散指标对步行设施的调整流程图 Figure 4 Flow chart of the layout adjustment of pedestrian facilities based on evacuation indicators |
具体步骤:1) 疏散空间面积调整.步行设施内行人疏散空间与障碍物空间面积之和一定的情况下,行人疏散空间与障碍物空间的面积变化属于“此增彼减”的过程,因此可以通过减少障碍物空间的占据面积来增加行人疏散空间的面积. 2) 疏散移动距离调整.行人疏散移动距离反映了行人疏散过程中移动距离对疏散过程的影响.可以通过调整障碍物布局或疏散瓶颈的位置,从而实现疏散移动距离的合理化. 3) 疏散瓶颈宽度调整.疏散瓶颈反映了行人疏散过程中拥挤排队对疏散过程的影响,而且瓶颈宽度是影响行人疏散时间的主要因素.可根据疏散瓶颈所分担的疏散面积,对瓶颈宽度进行拓宽与缩窄的调整;同时,可将疏散瓶看作该区域的安全出口,详细的调整过程可参考文献[4]. 4) 障碍物布局调整.障碍物布局不平衡系数反映了每层或每个节点的局部移动区域面积与瓶颈宽度匹配的合理程度.当理想分担率大于实际分担率时,应减少隶属集合内局部移动面积或者增大其瓶颈宽度;当理想分担率小于实际分担率时,应增加隶属集合内的移动面积或减小其瓶颈宽度.通过调整相应的移动区域面积与瓶颈宽度实现障碍物布局的平衡性,具体调整计算详见文献[13]. 5) 通过前4步调整直至所有节点和层的各项疏散指标均符合规范要求时,终止调整程序;否则,跳转到步骤1,继续调整.
然而,步行设施空间布局设计与调整是一个系统的优化过程,文章仅仅通过单向指标的逐步调整阐述了步行设施空间布局的调整流程,因此,系统最优化的步行设施内空间布局设计与调整是未来的主要研究内容.
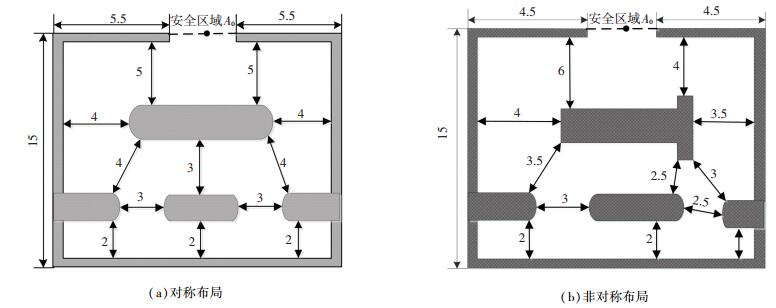
4 算例以某一级耐火建筑商场为例,对其进行步行设施疏散特征指标的计算与分析.该商场设计容纳人数为600人,设施空间为15 m×15 m的正方形,拥有一个安全出口,空间内部设施主要有矩形截面柜台4个,尺寸及布局如图 5(a)所示,障碍物的面积为75 m2.各个节点的面积为A1=14 m2、A2=A3=8 m2,A4=A5=12 m2,A6a=A6b=12 m2,A7=A8=6 m2,A9=A10=20 m2,A11a=A11b=7.5 m2,A12=A13=10 m2.

|
图 5 购物空间内障碍物布局尺寸和局部移动区划分示意图 Figure 5 The illustration of layout and size of obstacles and the division of movement area in shopping center |
根据该购物中心局部移动区域(如图 5(b)所示)的划分以及网络化的方法将该购物中心网络化,基于移动距离最短的疏散路径选择策略,得到购物中心的行人疏散树,如图 6所示.

|
图 6 购物中心疏散树示意图 Figure 6 The illustration of evacuation tree in shopping center |
由表 1、2分析可知,疏散面积、移动距离各单向指标大致符合要求.整体上看,行人疏散面积、行人疏散移动距离严格由第5到0层逐层递增,层L1、L2、L5的障碍物布局不平衡系数相对过大;从节点的角度分析,每个节点的平均疏散移动距离和加权疏散移动距离相差不大,节点A5、A7、A10的障碍物不平衡系数过大.依据各个疏散特征指标的计算,在不改变疏散空间物理结构的基础上,满足工程要求的前提下,对障碍物的布局进行调整,优化障碍物布局指标,使购物中心布局更加合理.得到调整后的购物中心障碍物布局如图 7所示.
| 表 1 购物中心节点疏散特征指标 Table 1 Spatial characteristics indexes in shopping center |
| 表 2 购物中心层疏散特征指标 Table 2 Spatial characteristics indexes in shopping center |
|
图 7 调整后购物中心移动空间布局示意图 Figure 7 The illustration of space layout in shopping center after adjustment |
特别需要补充说明的情况是,算例分析中给出了一个“对称”的障碍物调整布局方案,用以说明行人步行设施空间疏散特征指标的计算与障碍物空间布局调整.在疏散特征指标的计算过程中,文中存在一个基本的假设条件,即行人是均匀分布在疏散空间内的,因此“对称”的空间布局最容易满足疏散特征指标的评价要求,如图 7(a)所示.然而,在实际的工程应用中,由于建筑空间分布与使用的多样性,行人在步行设施内的空间布局是很难满足在移动区域内的均匀分布,因此在计算行人疏散移动距离与障碍物布局指标时,需要采用局部移动区域内的行人数量进行计算,以便更贴切实际地满足工程需要.当在特征指标计算评价过程中,不能获取各局部移动区域内的行人数量时,可以基于行人均匀分布于步行设施空间内的假设,采用局域移动区域的面积进行相关指标的计算评价.同时,为增加步行设施内建筑空间的多样性,以及减少行人疏散过程中的认知障碍,建议在满足步行设施疏散特征指标的基础上,根据实际情况进行多样化设计,如图 7(b)所示.
5 结论1) 基于行人步行设施的空间布局,将步行设施内空间划分为行人移动空间与障碍物空间;基于行人移动的瓶颈对步行设施移动空间的划分特征,提出了步行设施MOSD行人移动网络构建方法,从而将物理设施转化为行人移动网络,实现了步行设施空间疏散特征分析对象由连续空间转换为网络空间.
2) 基于移动距离最短的疏散路径选择策略,提出了步行设施行人疏散树的构建方法,从而将行人移动网络转化为疏散树;分析了疏散树中层与节点的隶属关系,再现了行人疏散移动过程中的层层递进关系,为步行设施空间疏散特征指标提供了计算依据.
3) 从影响步行设施内行人疏散的角度,基于疏散树节点与层的隶属关系,构建了包含疏散的空间面积、移动距离、瓶颈宽度、障碍物布局不平系数等指标的步行设施空间疏散特征指标体系;基于各项指标的内涵,提出了基于疏散树的指标计算方法.
4) 基于步行设施的类型、建筑物耐火等级、设计规范等,提出了各项指标的合理取值;提出了基于疏散的空间面积、移动距离、瓶颈宽度、障碍物布局不平系数等4项指标的逐步调整与循环校核的步行设施空间布局调整方法.结合算例,分析了步行设施空间布局的调整过程;并强调在实际的工程应用中,可采用局部移动区域内的行人数量进行各项指标值得计算.
| [1] |
CHENC X, LI Q, KANEKO S. Location optimization algorithm for emergency signs in public facilities and its application to a single-floor supermarket[J].
Fire Safety Journal, 2009, 44(1): 113-120.
DOI: 10.1016/j.firesaf.2008.05.006 |
| [2] |
岳昊, 邵春福, 关宏志, 等. 大型行人步行设施紧急疏散标志设置[J].
北京工业大学学报, 2013, 39(6): 120-125.
YUE Hao, SHAO Chunfu, GUAN Hongzhi, et al. Location method of emergency evacuation signs in large pedestrian facilities[J]. Journal of Beijing University of Technology, 2013, 39(6): 120-125. |
| [3] |
CHEN P, FENG F. A fast flow control algorithm for real-time emergency evacuation in large indoor areas[J].
Fire Safety Journal, 2009, 44(5): 732-740.
DOI: 10.1016/j.firesaf.2009.02.005 |
| [4] |
岳昊, 王帅, 张磊, 等. 行人步行设施紧紧疏散出口设置方法[J].
北京交通大学学报, 2014, 38(6): 1-6.
YUE Hao, WANG Shuai, ZHANG Lei, et al. Setting method of emergency exits in pedestrian walking facilities[J]. Journal of Beijing Jiaotong University, 2014, 38(6): 1-6. DOI: 10.11860/j.issn.1673-0291.2014.06.001 |
| [5] |
LO S M, HUANG H C, WANG P, et al. A game theory based exit selection model for evacuation[J].
Fire Safety Journal, 2006, 41(5): 364-369.
DOI: 10.1016/j.firesaf.2006.02.003 |
| [6] |
YUE Hao, GUAN Hongzhi, SHAO Chunfu, et al. Simulation of pedestrian evacuation with asymmetrical exits layout[J].
Physica A, 2011, 390(2): 198-207.
DOI: 10.1016/j.physa.2010.10.003 |
| [7] |
KOBES M, HELSLOOT I, VRIES B, et al. Way finding during fire evacuation; an analysis of unannounced fire drills in a hotel at night[J].
Building and Environment, 2010, 45(3): 537-548.
DOI: 10.1016/j.buildenv.2009.07.004 |
| [8] |
FANG Z, LI Q, Li Q, et al. A proposed pedestrian waiting-time model for improving space-time use efficiency in stadium evacuation scenarios[J].
Building and Environment, 2011, 46(9): 1774-1784.
DOI: 10.1016/j.buildenv.2011.02.005 |
| [9] |
TAVARES R M, GALEAE. R. Evacuation modeling analysis within the operational research context: a combined approach for improving enclosure design[J].
Building and Environment, 2009, 44(5): 1005-1016.
DOI: 10.1016/j.buildenv.2008.07.019 |
| [10] |
张军英, 谭泽阳. 国家体育场安全疏散设计[J].
建筑学报, 2009(9): 84-87.
ZHANG Junying, TAN Zeyang. Design for safe evacuation of the National Stadium[J]. Architectural Journal, 2009(9): 84-87. |
| [11] |
WU G Y, CHEN S W, HUANG Y T. Modeling the occupant evacuation of the mass rapid transit station using the control volume model[J].
Building and Environment, 2010, 45(10): 2280-2288.
DOI: 10.1016/j.buildenv.2010.04.015 |
| [12] |
宋卫国, 于彦飞, 陈涛. 出口条件对人员疏散的影响及其分析[J].
火灾科学, 2003, 12(2): 100-104.
SONG Weiguo, YU Yanfei, CHEN Tao. Influences of exit conditions on pedestrian evacuation[J]. Fire Safety Science, 2003, 12(2): 100-104. |
| [13] |
岳昊, 张旭, 陈刚, 等. 初始位置布局不平衡的疏散行人流仿真研究[J].
物理学报, 2012, 61(13): 84-94.
YUE Hao, ZHANG Xu, CHEN Gang, et al. Simulation of pedestrian evacuation with asymmetrical pedestrian layout[J]. Acta Physica Sinica, 2012, 61(13): 84-94. |
| [14] |
刘栋栋, 赵斌, 李磊, 等. 北京南站行人特征参数的调查与分析[J].
建筑科学, 2011, 27(5): 61-66.
LIU Dongdong, ZHAO Bin, LI Lei., et al. Survey and analysis of pedestrian characteristic parameters in Beijing South Railway Station[J]. Building Science, 2011, 27(5): 61-66. |
| [15] |
史建港. 大型活动行人交通特性研究[D]. 北京: 北京工业大学, 2007.
SHI Jiangang. Research on pedestrian traffic characteristics in special events[D].Beijing: Beijing University of Technology, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10005-2007189461.htm |
| [16] |
天津消防研究所. 建筑防火设计规范: GB 50016—2014[S]. 北京: 中华人民共和国住房和城乡建设部, 2015.
Tianjin Fire Research Institute. Code for fire protection design of buildings: GB 50016—2014[S].Beijing: Ministry of Housing and Urban Rural Development of People's Republic of China, 2015. |
| [17] |
李得伟, 韩宝明.
行人交通[M]. 北京: 人民交通出版社, 2011: 42-43.
LI Dewei, HAN Baoming. Pedestrian traffic[M]. Beijing: China Communications Press, 2011: 42-43. |
 2017, Vol. 49
2017, Vol. 49


