2. 中铁二院工程集团公司,成都 610031
2. China Railway Eryuan Engineering Group Co., Ltd., Chengdu 610031, China
正交异性钢桥面结构通常由钢桥面板、纵肋和横隔板组成,因其整体重量轻、施工方便和结构安全度大等特点,被广泛应用于大跨桥梁.运营过程中正交异性桥面板容易出现的两类病害为铺装层损坏和钢桥面焊接构造疲劳开裂[1],其中一个很重要原因是沥青混凝土钢桥面系刚度偏低[2].
国内外学者[3-7]为提升正交异性钢桥面板的疲劳性能,不断优化设计参数,改进构造细节,已经形成典型的构造形式并在规范中推荐使用,但随着交通量不断增加,疲劳开裂问题仍然突出,因此发展新型组合桥面板结构成为提升正交异性钢桥面板疲劳性能的主要发展方向和途径.组合桥面板的主要设计思路有二:1) 沿用传统正交异性钢桥面板的构造设计参数,顶板铺设薄层超高性能铺装混凝土材料,如RPC(活性粉末混凝土)、UHPC(超高性能混凝土)等.邵旭东等[2, 8]提出了薄层RPC组合桥面板,并在实桥中开始应用. Lamine[9]提出了超高性能纤维混凝土(UHPFRC)新型组合钢桥面板;2) 改进正交异性钢桥面板构造结构体系,采用大尺寸、大间距纵肋,同时增大横肋间距,并在顶板上铺设较厚且容许开裂的高性能混凝土结构层(混凝土层裂缝宽度满足规范要求)和沥青铺装层,这样可大量减少焊接构造数量,显著提高桥面板的局部刚度,大幅度降低各疲劳易损部位的应力水平,改善桥面铺装的受力状况,从而为钢桥面板疲劳开裂和桥面铺装易损提供整体解决方案[10-13].第二类思路的组合面板的研究成果大多为静力试验[10-11]和数值模拟[12],缺乏疲劳试验研究.
纵肋腹板与面板、纵肋腹板与横隔板这两类连接焊缝处容易出现疲劳开裂,劣化结构使用性能.文献[7]研究表明:增加桥面板厚度显著降低了纵肋腹板与顶板焊缝处应力,大幅度提高该细节疲劳寿命,因此新型正交异性钢-混组合桥面的顶板厚度增加,刚度提高,纵肋腹板与面板连接焊缝构造疲劳性能明显改善.但钢-混组合桥面的纵肋截面尺寸和间距增大,扭转刚度将大幅度增加,横桥向刚度分配不均匀程度随之增加,纵肋扭转变形也将明显变大,纵肋腹板与横隔板连接焊缝构造(弧形开口处)的疲劳问题更加复杂和突出.因此本文从理论分析和足尺模型试验两方面对这种新型正交异性钢混组合桥面结构进行研究,以期探明纵肋腹板与横隔板连接焊缝构造的疲劳机理和性能.
1 纵肋受力理论分析模型 1.1 模型说明及假定正交异性桥面构造复杂,一般采用复杂的空间有限元模型进行受力分析,但有限元结果只能反映荷载综合效应,很难区分扭转、弯曲和剪切等基本变形行为的影响效应,因此有必要以车轮荷载作用下正交异性钢混组合桥面板为分析对象,以纵肋的基本变形模式(扭转和弯曲)为研究内容进行分析,如图 1所示,并假定如下:1) 钢材和混凝土均为理想线弹性材料;2) 多纵肋桥面系简化成闭口纵肋截面与肋间桥面板铰接,且纵肋刚性扭转;3) 纵肋截面扭转为自由扭转;4) 纵肋扭转变形忽略混凝土层抗剪刚度;5) 横隔板面内无限刚性,面外无限柔性.
|
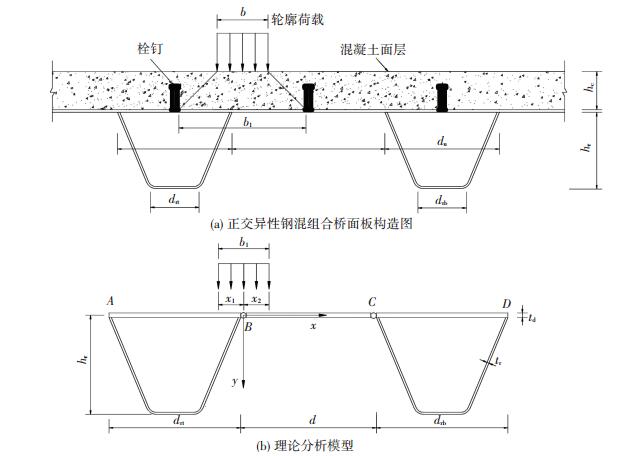
图 1 正交异性组合桥面板受力分析模型 Figure 1 Analytical model for orthotropic composite deck |
以纵肋腹板与顶板的接头B点为原点建立坐标系,疲劳车轮荷载分布集度为q,分布范围为a×b,经混凝土层45°扩散后作用于钢桥面的分布集度为q1,分布范围为a1×b1,且端部离B点距离分别为x1、x2;Hr和Hc分别为纵肋高和混凝土层厚度;纵肋上下底宽分别为drt和drb,截面外形轮廓线包围的面积为Ar,td和tr为顶板和纵肋的厚度,纵肋间净距为d,横隔板间距L;Tr和Qr为纵肋扭矩和弯曲剪力,如图 1所示.
根据欧洲规范[13],标准疲劳车轮荷载分布范围a×b=400 mm×400 mm,混凝土层45°扩散分布范围和分布集度q1分别
| ${{a}_{1}}={{b}_{1}}=400+2{{H}_{\rm{c}}},$ | (1) |
| ${{q}_{1}}=\rm{ }q{{\{400/(400+2{{H}_{\rm{c}}})\}}^{2}}.$ | (2) |
由式(2) 可知:Hc对荷载分布影响很大,当Hc=150 mm时,分布集度q1减少了2/3.
根据影响线加载,最不利状态为轮载部分或全部作用于纵肋上(x2≤b1),如图 1所示,可得纵肋间桥面板上轮载传给纵肋B和C点的荷载分别为q1a1x2(d-x2/2)/d和q1a1x22/d,则纵肋的扭矩Tr和弯曲剪力Qr分别为
| ${{T}_{\rm{r}}}=0.5{{q}_{1}}{{a}_{1}}[{{b}_{1}}{{d}_{\rm{rt}}}-{{({{b}_{1}}-{{x}_{2}})}^{2}}-0.5x_{2}^{2}{{d}_{\rm{rt}}}/d],$ | (3) |
| ${{Q}_{\rm{r}}}={{q}_{1}}{{a}_{1}}({{b}_{1}}-0.5x_{2}^{2}/d).$ | (4) |
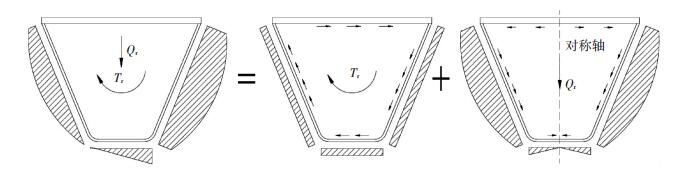
纵肋剪应力分析如图 2所示,自由扭转剪应力τ1,弯曲剪应力τ2和总剪应力τr (方向如箭头方向)分别为
|
图 2 纵肋剪应力分析 Figure 2 Shear stress in rib |
| ${{\tau }_{1}}={{T}_{\rm{r}}}/(2{{A}_{\rm{r}}}{{t}_{\rm{r}}}),$ | (5) |
| ${{\tau }_{2}}={{Q}_{\rm{r}}}{{S}_{\rm{r}}}/({{I}_{\rm{r}}}{{t}_{\rm{r}}}),$ | (6) |
| ${{\tau }_{\rm{r}}}={{\tau }_{1}}+{{\tau }_{2}}.$ | (7) |
式中: Ir为纵肋抗弯刚度,Sr为以顶(底)板对称轴为起点的纵肋腹板面积矩,tr为纵肋厚度.
将横隔板间的纵肋看作轮载作用的钢混组合梁(跨度为L)分析纵肋弯曲行为,其弯矩Mr和相应弯曲正应力σr为
| ${{\sigma }_{\rm{r}}}={{M}_{\rm{r}}}h/{{I}_{\rm{e}}}.$ | (8) |
式中Ie为钢混组合梁等效抗弯刚度,h为梁上的点到中性轴的距离.
根据式(1)~(8) 可得到纵肋的主应力情况.纵肋腹板主要承担剪力,且车轮作用下横隔板处的纵肋一般处于负弯矩区,纵肋腹板底部承担压应力,忽略其有利影响,则横隔板弧形开口处纵肋主拉应力Sr可简化为
| ${{S}_{\rm{r}}}={{\tau }_{\rm{r}}}.$ | (9) |
由理论分析模型可知:混凝土层厚度对车轮荷载分布范围(a1×b1)影响很大,对局部受力(弯矩、扭矩和剪力)分布有很大影响,且混凝土层增加了桥面系的抗弯刚度,减小了纵肋和面板的正应力.
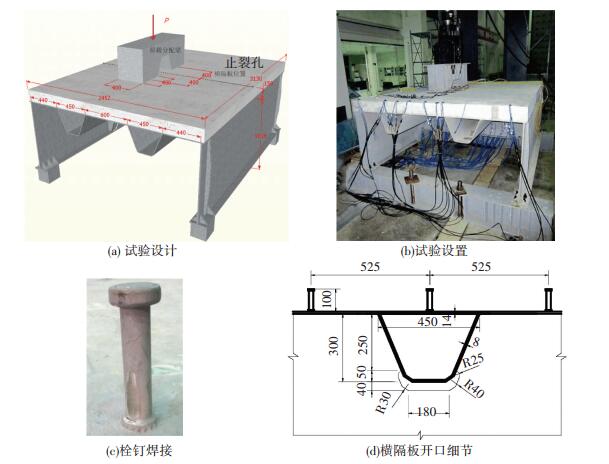
2 试验设计 2.1 试验概况基于某大桥正交异性钢混组合桥面结构节段设计,选择欧洲规范[13](EC3) 中480 kN标准疲劳车进行疲劳加载,根据实桥关键细节疲劳应力值和应力等效原则设计并制作了3.13 m×2.45 m×0.98 m足尺试验模型,其腹板、顶板、横隔板和U肋厚度分别为16、14、20、8 mm,Q345qD钢材.模型纵桥向中部设一道横隔板,横桥向上设两个U肋,肋间净距600 mm,顶板上铺150 mm厚,配钢筋网(Φ12钢筋)的C50混凝土,剪力键为长10 cm、直径19 mm的栓钉,栓钉间距(长和宽均为)525 mm,试验模型如图 3所示,焊接工艺按欧洲规范进行.根据实测,Q345qD钢材弹性模量205 GPa,屈服强度360 MPa,抗拉强度475 MPa. C50混凝土弹性模量34.7 GPa,抗压强度63.3 MPa.
|
图 3 疲劳试验模型 Figure 3 Fatigue test setup |
疲劳荷载由1 000 kN作动器通过分配梁两点作用于横隔板两侧等距离位置,由应力等效原则得到设计寿命期疲劳荷载为Pmin=20 kN,Pmax=320 kN,ΔP=300 kN,作动器与桥面板之间采用面积为400×400 mm的橡胶垫接触,试件端部用螺栓锚固于地基,如图 3(b)所示.
疲劳加载根据需要分两步:1) 设计寿命期疲劳试验.实桥疲劳荷载幅(300 kN)作用下加载200万次,验证细节设计的疲劳可靠性;2) 疲劳裂纹扩展试验.两倍实桥疲劳荷载幅作用下(Pmin=30 kN,Pmax=630 kN,ΔP=600 kN)继续加载100万次,按照疲劳S-N曲线(斜率取3),等效实桥疲劳荷载幅作用1 000万次,研究疲劳裂纹扩展情况.每隔一定周期对试件焊缝进行一次无损探伤,并每隔一定循环次数后进行一次静载试验,静载试验采用逐级加载,以观测试件是否出现裂纹及测点应变的变化规律.
2.3 应变监测及混凝土开裂观测在研究区域焊缝连接构造控制点位置粘贴应变片,且在试件跨中纵肋及肋间关键点处设置百分表监测梁的竖向挠度.横隔板,顶板和加劲肋连接构造区域(均在纵肋外表面)按一般焊缝应力的测量要求,离焊缝一定距离(板厚)布置应变片,各测点主拉应力由0°、45°、90°三向应变花实测得到.在混凝土层中的钢筋网和栓钉上亦对称布置应变片,栓钉上的应变片位于根部,且位置与纵肋长度方向平行且沿横隔板对称布置,如图 4所示.在混凝土层顶面画出方格线,利用裂缝观测仪观测每级荷载作用下裂缝开展及分布情况.

|
图 4 测试布置 Figure 4 Strain gauges setup |
根据试验模型建立正交异性组合桥面板空间有限元模型,如图 5所示.采用线弹性三维板壳单元模拟钢板,实体单元模拟C50混凝土层,板壳单元与实体单元采用节点耦合分析以模拟钢混组合行为,混凝土层不考虑钢筋网和栓钉,钢构造不考虑焊缝.钢材弹性模量206 GPa、泊松比0.3.模型端部被约束,在横隔板两侧各施加接触面为400 mm×400 mm的160 kN均布面荷载.根据计算精度要求划分单元尺寸,关键细节处尺寸为1 mm,其他为5 mm.

|
图 5 试件有限元分析模型 Figure 5 FEM model for specimen |
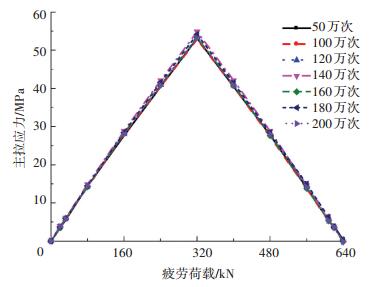
根据实桥节段模型在EC3标准疲劳车荷载作用下的应力计算结果,得到设计寿命期的细节疲劳荷载幅值.基于应力等效原理,疲劳试验模型采用实桥疲劳荷载幅进行200万次加载,验证细节设计疲劳强度.以横隔板弧形开孔处主拉应力较大的应变测点为应力控制点,为校核应力控制点处应力是否达到设计幅值,比较该处应力测点实测值及有限元计算值,如图 6所示,目标值为50.8 MPa,实测值在49.4~51.0 MPa.测点实测应变与荷载呈线性关系,多次静载实测应力值和目标值很接近,且加载和卸载过程中均具有很好的对称性和线弹性,表明试验模型能反映实桥受力情况,在疲劳荷载循环加载200万次过程中,正交异性组合钢桥面板构造细节力学行为未发生改变.
|
图 6 应力控制点应力变化曲线 Figure 6 Stress-loading curves of the reference point |
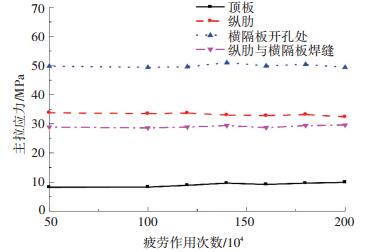
顶板、横隔板和纵肋交叉构造焊接细节关键位置应力实测如图 7所示,300 kN疲劳荷载幅作用下,顶板测点的主拉应力幅不超过10 MPa,而相应位置纵肋和横隔板测点的主拉应力幅都超过28 MPa,横隔板开孔处测点达到50 MPa,都远大于顶板测点应力值,由此可见:铺设混凝土层后,顶板刚度得到很大提高,因此应力水平最低,其疲劳性能得到明显改善.
|
图 7 顶板主拉应力幅变化曲线 Figure 7 Principal tensile stress range-cycle number relationship of deck |
图 8为300 kN疲劳荷载幅作用下横隔板上各关键点应力情况,括号内为有限元值.结果表明:有限元值和实测值较好吻合.测点越靠近顶板,应力值越小,说明顶板刚度较大.纵肋与横隔板连接焊缝处应力较大,开孔处应力最大,容易产生疲劳开裂.

|
图 8 横隔板关键点主拉应力幅(MPa) Figure 8 Principal tensile stress ranges of crossbeam(MPa) |
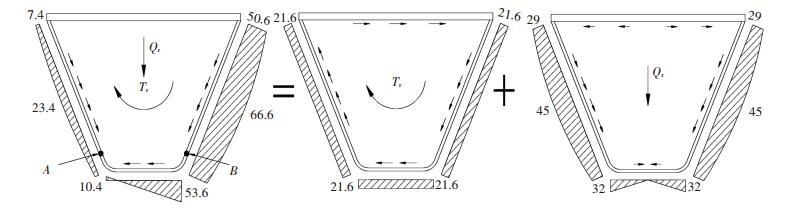
根据理论模型得到纵肋剪应力分布理论值如图 9所示,A和B为纵肋腹板与横隔板弧形开口交叉焊缝以下10 mm纵肋上的测点,A点的实测值、有限元值和理论值分别为8.7、9.3、10.5;B点的实测值、有限元值和理论值分别为49.2、50.6、53.8.纵肋腹板剪应力理论值与实测值及有限元值吻合得较好.由于忽略混凝土层抗剪强度及横隔板约束,理论值比实测偏大.考虑到焊缝附近区域应力梯度较大,实测应力为一定区域的平均应力值,因此理论值与实测值合理吻合.从纵肋剪应力理论值组成可见,扭转剪应力为21.6 MPa,弯曲剪应力为29~45 MPa,扭转剪应力占总剪应力值30%以上.纵肋腹板与横隔板弧形开口交叉焊缝处的扭转效应尤其明显,容易疲劳开裂.
|
图 9 纵肋理论剪应力分布 Figure 9 Predicted shear stress distribution of rib |
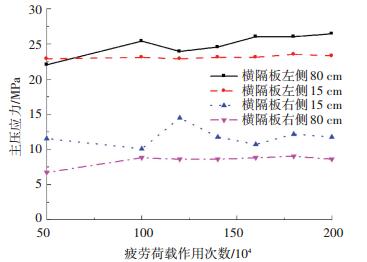
横隔板上方的混凝土层因负弯矩产生超过3 MPa的主拉应力,在疲劳荷载作用一万次后即发生开裂,如图 10所示,而且随着次数增加,裂纹宽度基本不变,裂缝长度和数量增加. 200万次疲劳加载后,最大裂缝宽度为0.135 mm,考虑到混凝土上面还有防水层和铺装,裂缝宽度可以满足耐久性要求.钢筋应力变化不大,大多数测点主拉应力在15 MPa以下,且应力与荷载呈线性关系,最大主拉应力实测结果如图 11所示.混凝土开裂后,荷载因钢筋传力而重分布,因此裂缝长度和数量增加,但宽度基本不增加.

|
图 10 混凝土层开裂情况 Figure 10 Cracking of the concrete slab |
|
图 11 同一钢筋不同位置主拉应力幅 Figure 11 Principal stress ranges of different positions in the reinforcement |
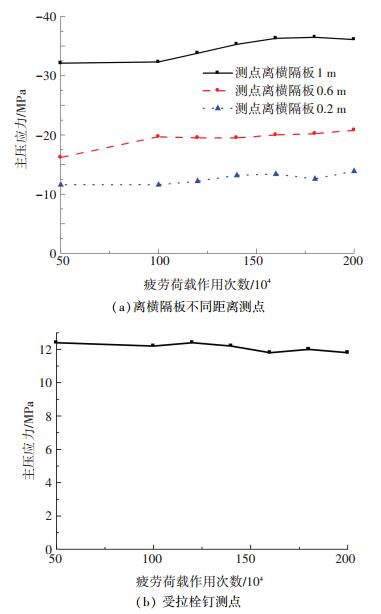
图 12为栓钉测点应力情况,疲劳荷载作用下混凝土层与钢顶板产生滑移,大部分栓钉测点为不超过15 MPa的主压应力.栓钉剪力跟滑移量有很大关系,离加载点距离越远,滑移量往往越大,栓钉受力也越大,如图 12(a)中两个离加载处不同距离测点的应力情况.由于纵肋的扭转变形和横隔板处产生的负弯矩效应,导致混凝土与钢顶板的脱离现象,即“掀起”效应,此时栓钉受到拉应力,如图 12(b)所示.
|
图 12 栓钉测点主应力幅与循环次数变化曲线 Figure 12 Principal stress range-cycle number relationship of studs |
为研究新型正交异性钢混组合桥面板的疲劳强度储备,分析其疲劳裂纹扩展行为,在完成设计寿命期200万次疲劳循环加载试验后,开展超长服役期内超负荷疲劳试验研究,进行200~300万次循环加载时,疲劳荷载幅为600 kN,即达到设计期疲劳荷载幅的两倍.
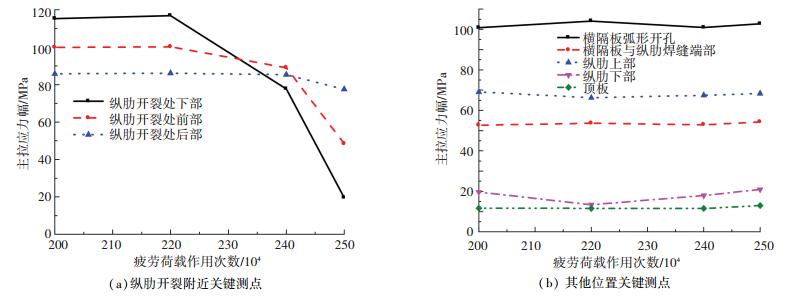
3.2.1 应力分析疲劳荷载幅增加到600 kN后,对各关键测点主拉应力进行监测,发现实测主拉应力与荷载基本保持线性关系. 250万次循环后,横隔板与U形肋焊缝焊趾处观察到长度为18 mm的疲劳裂纹,按照疲劳S-N曲线(斜率取3),此时总疲劳加载次数应该等效于实桥疲劳荷载作用次数600万次. 200~220万次循环,横隔板与纵肋底部焊缝焊趾测点处主拉应力幅变化很小;220~250万次循环加载过程中逐步降低,表明焊趾测点处萌生了疲劳裂纹,周围区域应力重分布,且测点应力随裂纹扩展逐渐变小,尤其是裂纹下部测点应力降低最明显,如图 13(a)所示. 200~250万次循环加载过程中其他关键测点应力荷载曲线如图 13(b)所示,远离开裂处各关键点的主拉应力幅变化很小,且试验模型实测整体位移变化也很小,说明开裂是局部行为,对整体刚度影响不大.
|
图 13 纵肋-横隔板焊接构造关键测点主拉应力幅与循环次数关系曲线 Figure 13 Principal tensile stress range-cycle number relationship of key points |
250万次疲劳荷载作用后,横隔板与纵肋腹板焊缝焊趾处疲劳裂纹沿基本平行于纵肋长度方向扩展,并有向纵肋腹板上部扩展的趋势,且扩展速率很快.裂纹长度约100 mm时,在裂尖钻直径6~8 mm止裂孔,但裂纹扩展速率仍然很快,最后总长度达到230 mm,如图 14所示.从试件上切割下疲劳裂纹部分采用扫描电镜(SEM)进行疲劳断口分析,如图 15所示.裂纹萌生于焊趾,然后沿纵肋板厚方向扩展,穿透后快速向长度方向扩展.横隔板约束了纵肋截面扭转变形,车轮荷载作用下纵肋局部产生了较大面外变形,因此离横隔板左右一倍板厚(20 mm)范围,纵肋疲劳断口显示为弯-拉应力断口,其他区域为受拉断口.

|
图 14 纵肋裂纹扩展情况 Figure 14 Crack of the rib-to-diagram weld |

|
图 15 纵肋疲劳断口分析 Figure 15 Fatigue fracture of the rib |
1) 通过新型正交异性钢混组合桥面板纵肋与横隔板焊接构造细节疲劳机理的理论和足尺模型疲劳试验分析,将正交异性组合桥面简化成铰接的双纵肋受力计算模型,与实测结果对比证明了双纵肋模型力学概念明确,能合理反映纵肋实际力学行为.
2) 铺设混凝土层后顶板应力水平大幅度降低,疲劳性能得到很大改善,但车轮荷载作用下纵肋扭转变形明显,纵肋腹板和横隔板焊接连接细节下部应力较大,容易产生裂纹.
3) 混凝土层开裂对桥面钢结构焊接细节应力水平影响很小.混凝土层与钢桥面间产生滑移,混凝土层与钢桥面间存在“掀起”效应,可能引起栓钉的疲劳破坏.
| [1] |
WOLCHUK R. Lessons from weld cracks in orthotropic decks on three European bridges[J].
Journal of Structural Engineering, 1990, 116(1): 75-84.
DOI: 10.1061/(ASCE)0733-9445(1990)116:1(75) |
| [2] |
SHAO Xudong, YI Dutao, HUANG Zhengyu, et al. Basic perfor-mance of the composite deck system composed of orthotropic steel deck and ultra-thin RPC layer[J].
Journal of Bridge Engineering, 2013, 18(5): 117-128.
|
| [3] |
陶晓燕. 正交异性钢桥面板节段模型疲劳性能试验研究[J].
中国铁道科学, 2013, 34(4): 22-26.
TAO Xiaoyan. Experimental study on the fatigue performance of the section model of orthotropic steel bridge deck[J]. China Railway Science, 2013, 34(4): 22-26. |
| [4] |
王春生, 付炳宁, 张芹, 等. 正交异性钢桥面板足尺疲劳试验[J].
中国公路学报, 2013, 26(2): 69-76.
WANG Chunsheng, FU Bingning, ZHANG Qin, et al. Fatigue test on full-scale orthotropic steel bridge deck[J]. China Journal of Highway and Transport, 2013, 26(2): 69-76. |
| [5] |
张清华, 崔闯, 卜一之, 等. 港珠澳大桥正交异性钢桥面板疲劳特性研究[J].
土木工程学报, 2014, 47(9): 110-119.
ZHANG Qinghua, CUI Chuang, BU Yizhi, et al. Study on fatigue features of orthotropic decks in steel box girder of the Hong Kong-Zhuhai-Macao bridge[J]. China Civil Engineering Journal, 2014, 47(9): 110-119. |
| [6] |
叶华文, 徐勋, 强士中, 等. 重庆两江大桥正交异性钢桥而板疲劳性能试验研究[J].
中南大学学报(自然科学版), 2013, 44(2): 749-756.
YE Huawen, XU Xun, QIANG Shizhong, et al. Fatigue test of orthotropic steel bridge deck in Chongqing liangjiang bridge[J]. Journal of Central South University(Science and Technology), 2013, 44(2): 749-756. |
| [7] |
SIM H B, UANG C M. Stress analyses and parametric study on full-scale fatigue tests of rib-to-deck welded joints in steel orthotropic decks[J].
Journal of Bridge Engineering, 2012, 17(5): 765-773.
DOI: 10.1061/(ASCE)BE.1943-5592.0000307 |
| [8] |
丁楠, 邵旭东. 轻型组合桥面板的疲劳性能研究[J].
土木工程学报, 2015, 48(1): 74-81.
DING Nan, SHAO Xudong. Study on fatigue performance of light-weighted composite bridge deck[J]. China Civil Engineering Journal, 2015, 48(1): 74-81. |
| [9] |
LAMINE D, PIERRE M, FERNANDA G, et al. Use of UHPFRC overlay to reduce stresses in orthotropic steel decks[J].
Journal of Constructional Steel Research, 2013, 89: 30-41.
DOI: 10.1016/j.jcsr.2013.06.006 |
| [10] |
ROLF J, TOBIASM. The ortho-composite-slab of the elbebridge wittenberge[C]//IABSDE Symposium Report: Engineering for Progree Nature and People. Madrid: IABSE, 2014, 1186-1191.
|
| [11] |
苏庆田, 贺欣怡, 曾明根, 等. T形肋正交异性组合桥面板力学性能[J].
同济大学学报(自然科学版), 2016, 44(3): 341-347.
SU Qingtian, HE Xinyi, ZENG Minggen, et al. Mechanical properties of T shaped rib orthotropic composite bridge deck[J]. Journal of Tongji University (Natural Science Edition), 2016, 44(3): 341-347. |
| [12] |
张清华, 郭伟峰, 崔闯, 等. 新型大纵肋正交异性钢—混凝土组合桥面板疲劳特性研究[J].
公路, 2015(12): 71-77.
ZHANG Qinghua, GUO Weifeng, CUI Chuang, et al. Research on fatigue features of new large longitudinal rib steel-concrete compo-site orthotropic deck[J]. Highway, 2015(12): 71-77. |
| [13] |
European Committee for Standardization. Fatigue strength of steel structures:EN1993-1-9 [S]. Brussels: ECS, 2005.
|
 2017, Vol. 49
2017, Vol. 49


