2. Atkins, Austin 78730, Texas, USA
2. Atkins, Austin 78730, Texas, USA
车辆换道是最为常见的驾驶行为表现之一,对交通流及交通安全有重要影响.根据驾驶员动机的不同,换道行为可分为两类:强制换道和自主换道[1-2].驾驶员为完成其正常的行驶目的而不得不采取的换道行为称为强制换道;驾驶员为获得优于当前车道的行驶条件而进行的变道行为,称为自主性换道.生存分析(survival analysis)是一种根据实验或调查数据,对生物、人以及具有类似生存规律的其他事物的生存时间进行分析和推断的统计方法[3].目前生存分析已被广泛应用于生物统计、医学、金融和工业工程等领域,近年来也逐渐被运用到交通运输领域,比如用来研究交通事故的清理时间[4-5]、出行行为[6]、机动车持有时间及报废时间[7]、城市道路混合交通行为[8]、高速公路危险区交通冲突发生风险率[9]、交通拥堵持续时间[10-11]等.同时, 无人驾驶逐渐成为领域内研究的热点,高速动态环境下的车辆换道行为[12]、车辆互联环境下的换道行为[13]亟待研究.生存分析方法在研究事件持续时间及其影响因素方面具有一定的优势.鉴于目前尚无生存分析在车辆换道耗时方面的研究,因此,本文基于无人机摄像获取包茂高速陕西境内某路段施工作业区车辆换道数据,运用生存分析中的比例风险模型,分析了车辆在养护施工作业区的换道持续时间(即换道耗时)及其两个重要的影响因素,希望为交通管理控制提供一定的科学依据,为高速动态环境下的高速公路车辆换道行为建模及仿真提供一定的理论基础.
1 生存分析方法生存分析将事件的结果和出现此结果所经历的时间结合起来分析,也称之为风险模型(hazard model)[14],亦称事件史分析(event history analysis),通常是用来探讨特定的风险变量与持续时间(duration)的关联性.不同于其他多因素分析方法(如线性回归、Logistic回归等),生存分析考虑了每个观测出现某一结局的时间长短,并且可以考虑删失数据(censored data),也不需要假定数据服从明确的参数分布.广义的持续(生存)时间是指从某个起始事件开始到某个终点事件的发生所经历的时间[3],也称为失效时间.
2 换道耗时生存函数 2.1 换道耗时模型结构目标车辆换道耗时T的累计分布函数为
| $F\left( t \right) = P\left( {T \le t} \right) = \int\limits_0^t {f\left( x \right){\rm{d}}x,} \quad \forall t \ge 0.$ | (1) |
生存函数定义为生存时间大于某给定时间t的概率,即换道时间大于t的概率,则目标车辆换道耗时为t的生存函数为
| $S\left( t \right) = P\left( {T > t} \right) = 1 - F\left( t \right) = \int\limits_t^\infty {f\left( x \right){\rm{d}}x,} \quad \forall t \ge 0.$ | (2) |
换道耗时T的风险函数h(t),其表示车辆开始变道后即发生横向位移,换道时间T已经持续到t的情况下,它在时间Δt内完成换道过程行驶至目标车道中心线的条件概率,可表示为
| $\begin{array}{l} h\left( t \right) = \mathop {{\rm{lim}}}\limits_{\Delta t \to 0} \frac{{P(t < T < t + \Delta t|T \ge t)}}{{\Delta t}} = \\ \quad \quad \quad \mathop {{\rm{lim}}}\limits_{\Delta t \to 0} \frac{{S\left( t \right) - S(t + \Delta t)}}{{\Delta t\Delta S\left( t \right)}},\forall t \ge 0. \end{array}$ | (3) |
对传统数据的解释性变量而言,加速失效模型为经典线性模型结构提供了一种直接的扩展方法(如Toeldo线性模型),但对存在删失的数据而言,加速失效模型的应用受到了误差分布的限制,因此采用乘法风险率模型(半参数模型)对换道耗时数据进行回归分析.
协方差向量Z的条件风险概率等于基本风险率h0(t)与非负协方差函数c(βZ)的乘积,即
| $h\left( {t/Z} \right) = {h_0}\left( t \right)c\left( {\beta Z} \right),\forall t \ge 0.$ | (4) |
式中:h0(t)为基准风险函数;Z为影响因素向量;β为对应影响因素的系数向量.
一般实际应用模型时,h0(t)可以有特定的参数形式,也可以是任意的非负函数形式;而连接函数c(βZ)大多采用Cox模型c(βZ)=exp(βZ),则式(4) 可写成
| $h\left( {t/Z} \right) = {h_0}\left( t \right){\rm{exp}}\left( {\beta Z} \right),\forall t \ge 0.$ | (5) |
为了研究施工作业区车辆换道耗时及其影响因素,选取包茂高速陕西境内某路段施工作业区进行调研.采用大疆Phantom4无人机对养护施工作业区进行高空监控摄像,采集了相关变量数据.由于试验设计、观测时间的局限,以及车辆在行驶进入或驶出试验路段时的个体差异,同时存在着完全数据和删失数据,只有在调查区域范围内完成全部换道行为的车辆样本数据才称为完全数据.综合现有车辆换道行为研究的相关文献,结合实地调研观测,另外结合数据采集的难易程度等几方面,进行车辆换道过程潜在影响变量的选取,最终选取其中两类变量进行分析研究,名义变量车型VehT(Z1)和交通时段Period(Z2).车型包括小型车、中型车和重型车,分别用0、1、2表示;交通时段分为高峰期、过渡期和非高峰期,亦分别用0、1、2表示.在调查中发现,重型车多数靠右行驶,且换道比例极小,故不对其进行分析,车型分类中仅考虑小型车和中型车.
4 数据建模与应用分析 4.1 统计分析可用调查案例269例,完全数据238例,占总案例的88.5%;删失数据31例,占总案例的11.5%.样本平均换道耗时是9.87 s,标准差为5.67 s,最长换道耗时是21 s,最短换道耗时为2 s.
4.2 基于Cox模型的估计结果多分类变量均以第1类作为参照水平(即分类变量值为0,如车型变量以小型车作为参照水平),得到的参数估计结果见表 2.表中第6列给出了各协变量参数估计的显著水平.
由表 2中的估计结果,可以得出换道耗时的风险模型,即考虑车型和时段的施工作业区车辆强制换道耗时的Cox比例风险模型为
| $\ln \frac{{h\left( {t/Z} \right)}}{{{h_0}\left( t \right)}} = 0.094{Z_1} + 0.392{Z_{21}} + 2.595{Z_{22}}.$ |
| 表 1 参数估计结果 Table 1 Estimated parameters for the hazard-based analysis |
图 1根据生存分析给出了半参数方法计算得到的生存函数.该图能反映施工作业区车辆换道实施过程中的换道在某时刻完成的概率.由图形可知随着换道耗时的增加,生存函数的一般变化趋势;生存函数下降的速度随换道耗时的变化而变化.
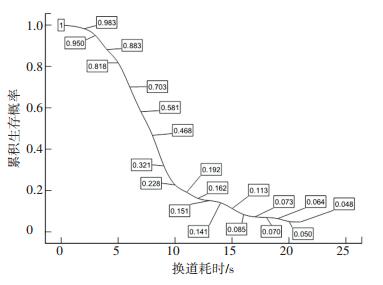
|
图 1 施工作业区车辆换道耗时的生存曲线 Figure 1 Survival curve for MLC duration in work zone |
可以将换道完成概率分成以下几种情况:1)0~3 s生存函数下降的速度十分平缓,即在这个时间段完成换道的车辆很少,大部分车辆“生存”了下来,亦即失效事件发生概率很小. 2)3~10 s为生存函数下降趋势非常快的阶段,大量的换道车辆完成换道.从图中可知,近80%的换道车辆在9 s以内完成换道. 3)10~16 s内为生存函数波动下降期,其中又可分为10~14 s和14~16 s两个时间段,10~14 s生存函数的下降速度明显大于14~16 s.可以看出施工作业区约15%的换道车辆的换道耗时在10~16 s之间. 4) 少量施工作业区换道车辆的换道耗时在16~20 s.
4.4 因素分析 4.4.1 车型对养护施工作业区车辆换道耗时的影响根据生存分析的非参数估计方法,可以得到不同样本下的生存函数,图 2给出了不同类型机动车换道耗时的差异.

|
图 2 基于Cox模型的不同车辆类型生存曲线 Figure 2 Survival curve for MLC duration of different vehicle types based on Cox model |
车型(VehT)是二分类协变量(0为小型车、1为中型车),其系数估计值为0.094,相对风险为e0.094=1.099,表明中型车的强制换道结束的风险略高于小型车,是小型车换道耗时的1.099倍.但该系数的SE相对较大,为0.178,表明该系数的点估计量不精确而应该计算区间的估计量.该系数的95%置信区间为0.094±1.96×0.178,即(-0.255,0.443);对应的相对风险的95%置信区间为(e-0.255,e0.443),即(0.775,1.557).风险率的置信区间包含1,说明车型(VehT)在Cox模型中的重要性应该小心地解释,亦即车型(VehT)对车辆在养护施工作业区换道耗时的影响并不显著(检验p值为0.595>0.05),从图 2中的累积生存函数曲线中也可以看出.
4.4.2 时段对养护施工作业区车辆换道耗时的影响时段为三分类协变量(0表示高峰期,1表示过渡期,2表示平峰期),协变量Z21(过渡期/高峰期)系数的估计值为0.392,表明过渡期养护施工作业区的车辆换道结束的风险为高峰期的e0.392=1.48倍;Z22(平峰期/高峰期)系数的估计值为2.595,表明平峰期养护施工作业区的车辆换道结束的风险为高峰期的e2.595=13.40倍. 图 3给出了分时段车辆换道耗时的生存函数.

|
图 3 基于Cox模型的分时段车辆换道耗时生存曲线 Figure 3 Survival curve for MLC duration during different time periods based on Cox model |
从图 3的生存函数曲线也可以看出,对于相同的换道耗时,平峰期的累积生存率明显低于高峰期和过渡时期,而高峰期的累积生存率最高;从曲线的斜率来看,在平峰期,车辆换道耗时小于6 s的风险率,比在过渡期和高峰期都高;在平峰期换道车辆中换道耗时短的车辆比重显著高于高峰期和过渡期.
5 结论1) 采用生存分析方法构建的高速公路施工作业区车辆强制换道耗时生存模型可定量分析各因素对车辆换道耗时的影响效果.
2) 近77%的换道车辆在10 s以内完成换道,施工作业区少量换道车辆的换道耗时在16~20 s.未发现养护施工作业区小型车和中型车的强制换道耗时的有显著性差异.
3) 养护施工作业区换道车辆在高峰期、过渡期及平峰期的换道耗时特征存在显著差异.其中,过渡期车辆换道结束风险为高峰期的1.48倍,平峰期则约为高峰期的13.40倍;对于相同的换道耗时,平峰期的累积生存率低于高峰期和过渡期,平峰期换道耗时较短的车辆所占比例较高峰期和过渡期高.
4) 文中仅对车辆换道行为的2个主要影响因素进行了分析,未来有必要针对其他的一些因素,如目标车辆速度、距合流点的距离、与目标车道前后车的距离等进行进一步的研究.
| [1] |
AHMED K I. Modeling drivers' acceleration and lane changing behavior[D]. Cambridge: Massachusetts Institute of Technology, 1999.
|
| [2] |
ZHANG Y, OWEN L E, CLARK J E. Multi-regime approach for microscopic traffic simulation[C]//Transportation Research Board: Transportation Research Record. Washington DC: Transportation Research Board, 1998: 103-115.
|
| [3] |
LEE E, WANG J.
Statistical methods for survival data analysis [M]. 4th ed. Hoboken, New Jersey: John Wiley & Sons, Inc, 2013.
|
| [4] |
MANNERING F L. Male/female driver characteristics and accident risk: some new evidence[J].
Accident Analysis & Prevention, 1993, 25(1): 77-84.
DOI: 10.1016/0001-4575(93)90098-H |
| [5] |
NAM D, MANNERING F. An exploratory hazard-based analysis of highway accident duration[J].
Transportation Research Part A, 2000, 34(2): 85-102.
DOI: 10.1016/S0965-8564(98)00065-2 |
| [6] |
KHAROUFEH J P, GOULIAS K G. Nonparametric identification of daily activity durations using kernel density estimators[J].
Transportation Research Part B, 2007, 36(1): 59-82.
DOI: 10.1016/S0191-2615(00)00038-2 |
| [7] |
CHANG H L, YEH T H. Regional motorcycle age and emissions inspection performance: a Cox regression analysis[J].
Transportation Research Part D, 2006, 11(5): 324-332.
DOI: 10.1016/j.trd.2006.06.004 |
| [8] |
HAMED M M. Analysis of pedestrians' behavior at pedestrian crossings[J].
Safety Science, 2001, 38(1): 63-82.
DOI: 10.1016/S0925-7535(00)00058-8 |
| [9] |
SHARMA A, BULLOCK D, PEETA S. Estimating dilemma zone hazard function at high speed isolated intersection[J].
Transportation Research Part C, 2011, 19(3): 400-412.
DOI: 10.1016/j.trc.2010.05.002 |
| [10] |
STATHOPOULOS A, KARLAFTIS M G. Modeling duration of urban traffic congestion[J].
Journal of Transportation Engineering, 2002, 128(6): 587-590.
DOI: 10.1061/(ASCE)0733-947X(2002)128:6(587) |
| [11] |
周映雪, 杨小宝, 环梅, 等. 基于生存分析的城市道路交通拥堵持续时间研究[J].
应用数学和力学, 2013, 34(1): 98-106.
ZHOU Yingxue, YANG Xiaobao, HUAN Mei, et al. Survival analysis approach for estimating urban traffic congestion duration[J]. Applied Mathematics and Mechanics, 2013, 34(1): 98-106. DOI: 10.3879/j.issn.1000-0887.2013.01.010 |
| [12] |
王政. 智能车辆自主换道方法的研究[D]. 长春: 吉林大学, 2016.
WANG Zheng. Research on autonomous lane changing method of intelligent vehicle[D]. Changchun: Jilin University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10183-1016079585.htm |
| [13] |
TALEBPOUR A, MAHMASSANI H S, HAMDAR S H. Modeling lane-hanging behavior in a connected environment: a game theory approach[J].
Transportation Research Part C: Emerging Technologies, 2015, 59: 216-232.
DOI: 10.1016/j.trc.2015.07.007 |
| [14] |
LAWLESS J F.
Statistical models and methods for lifetime data[M]. New York: John Wiley & Sons, Inc, 2002.
|
 2017, Vol. 49
2017, Vol. 49


