中国沥青路面设计采用以结构分析为基础的经验理论设计方法.无限半空间弹性层状体系理论是沥青路面结构分析的主要理论依据.其中，回弹模量是材料本构模型中的重要参数.路面结构分析中，通常对同一层材料采用统一的模量值.然而，随应力条件的改变，路面材料的回弹模量会产生变化，导致结构分析结果和道路的实际受力状态存在差别^[1-2].确定沥青稳定碎石回弹模量的应力依赖特性，建立非线性应力依赖本构模型，并将其应用于路面结构分析，是提高沥青路面结构分析准确性的必要基础之一.

回弹模量是一种近似的弹性模量.路面材料在动态和静态荷载条件下的力学响应显著不同^[3-4].道路在实际环境中受到车辆动载的重复作用，因此在室内回弹模量测试过程中，有必要采取相应的动态加载来更好的拟合实际情况.动态三轴实验是测试道路材料在不同应力条件下回弹模量的主要实验手段.实验时通过变换围压和竖向荷载的大小来近似模拟材料在路面结构中的受力状态.

基于室内三轴试验的结果，Seed等发现在对数坐标内，回弹模量和围压呈线性关系，并提出了首个体现应力依赖性的非线性回弹模量模型^[2].随后，Hicks和Monismith将体应力(3个主应力之和)引入到模型中，提出了著名的k-θ模型，该模型是被使用最为广泛的非线性回弹模量模型^[5].该模型的不足之处是，剪应力的对材料的影响未能体现^[6].为了弥补这一不足，重复荷载(s_d)被引入到模型中，重复荷载和材料中的剪应力大小直接相关，由此Uzan模型被提出^[7].由于路面结构是三维结构，并且在三轴试验过程中，试件的受力状态也是三维的，因此Witczak and Uzan将Uzan模型中的重复荷载替换为八面体剪应力^[8].为使模型能够同时使用英制单位和国际单位，大气压力被引入模型使等号两侧成为无量纲数值^[8]，新的模型被称为Universal Soil Model.然而，当材料处于较小剪应力状态下，Universal Soil Model会低估材料的回弹模量^[9]，因此NCHRP 1-28A项目对该模型进行了改进，加入了k₆和k₇^[10], 该模型非线性模型并且无法转化成为线性模型, 公式中回归常数的计算复杂，计算结果取决于初始值、求解算法和收敛标准的选择.实际应用中较难控制且不易推广.当k₆设置为0，k₇设置为1时，模型被简化为${M_R} = {k_1}{P_a}{\left( {\frac{\theta }{{{P_a}}}} \right)^{{k_2}}} \cdot {\left( {\frac{{{\tau _{{\rm{oct}}}}}}{{{P_a}}} + 1} \right)^{{k_3}}}$，能够转化为线性公式, 该公式被最新的美国经验力学路面设计方法(MEPDG)采用，用作粒料(如级配碎石)和土的回弹模量表达式^[11]，该模型也被我国《公路路基设计规范》JTG D30所采纳，用于表征和预估路基土的回弹模量.应力依赖回弹模量模型能够较为精确表达材料在实际路面结构中的力学特性，研究人员也采用三轴试验对路基土回弹模量的应力依赖特性进行测试，并使用k-q^[12]、Uzan^[12]和MEPDG^[13-15]模型对试验结果进行分析、拟合，结果表明这两种模型能够较为准确的描述回弹模量的应力依赖特性.然而，应力依赖特性无法应用于目前沥青路面结构设计所使用的无限半空间弹性层状体系理论.虽然能够通过将单个路面结构层划分成多个结构层，并赋予相应的模量来近似实现材料模量沿竖直方向的变化，但无法实现模量沿水平方向的变化.使用有限单元法，能够将路面结构被划分为不同微小单元，随应力状态的变化，计算并赋予单元不同的模量值^[16].因此，使用通用有限元软件并对所建立的应力依赖回弹模量模型编程，是解决路面结构分析过程中材料非线性应力依赖特性的有效有段^[17].科研人员已利用k-θ^[18]和Universal Soil Model^[19-20]作为材料研究采用动三轴试验，测试沥青稳定碎石不同应力状态的回弹模量，采用MEPDG模型建立材料的非线性应力依赖本构模型；采用Abaqus有限元软件中的UMAT子程序编程并定义沥青稳定碎石的本构模型，进行基于沥青稳定碎石非线性应力依赖本构模型的路面结构数值模拟.

1 动态三轴回弹模量测试

目前国内道路材料领域尚无动态三轴实验规范，研究主要参考美国AASHTO-T307规范进行回弹模量测试.测试系统主要由力学试验机和的三轴仪构成.力学实验机采用可编程控制的电压伺服液压加载系统，能够实现10 Hz的动态加载和200 Hz的数据读取频率. 图 1为三轴仪，实验过程中通过控制进气口的气压，控制试件的围压，从而模拟材料在路面结构中所处的应力状态.试件两侧加装量程为±0.5 mm的LVDT位移传感器.试件上下各放置一片抗摩擦片，材质为特氟龙.放置抗摩擦片的主要目的为尽量减小压头对试件施加的水平荷载.在实验开始之前，首先对试件加载1 000个循环的调节荷载(conditioning load)，用来移除试件和三轴仪不良接触对实验结果的影响.实验采用5个围压等级：20.7、34.5、68.9、103.4 kPa和137.9 kPa，每个围压等价加载3个等级的竖向荷载，共15种应力状态(图 2)，每种应力状态下施加200个加载循环，每一个加载循环由0.1秒的半正弦波和0.9秒的间歇时间构成.测试温度为20 ℃.

实验采用直径10 cm，高15 cm的圆柱形试件.沥青稳定碎石试件采用旋转压实仪制备(15 cm直径)，使用取芯机钻取直径10 cm的芯样，再切去试件的顶部和底部得到最终试件.研究采用3个沥青质量分数分别为2.5%，3.5%和4.5%.

2 沥青稳定碎石应力依赖特性

动态三轴实验结果显示：沥青稳定碎石的回弹模量显著受到应力状态的影响.以沥青含量3.5%为例(图 3)，在固定温度和荷载频率下，对应不同的应力状态沥青稳定碎石的回弹模量最低值为2 000 MPa；最高值为3 500 MPa，约为最低值的175%.研究采用体应力(θ=s₁+s₂+s₃)和八面体剪应力(τ_oct)表示沥青稳定碎石在空间中的应力状态.实验结果表明：回弹模量随体应力的增加而增加，随剪应力的增加而减小.沥青混合料弹性模量的应力依赖特性由石料颗粒间的相互作用导致(图 4).当颗粒材料受到围压的作用，颗粒间的接触面积增大，从而导致接触劲度(stiffness)的增加，材料内部有数以万计的接触点，从而导致宏观上材料弹性模量的增加.剪应力使颗粒间产生滑动或转动的趋势，从而模量减小.由于沥青粘结材料的加入，粒料间的连接被加强，应力依赖特性被减弱.

研究采用MEPDG回弹模量模型来拟合实验结果，构建回弹模量应力依赖模型.不同沥青含量沥青稳定碎石回弹模量模型的回归参数见表 1. 3种材料的模型回归相关系数均大于98%，表明该模型适用于构建沥青稳定碎石的回弹模量应力依赖模型.

3 有限单元法中应力依赖回弹模量建模

研究采用Abaqus有限元软件模拟基于沥青稳定碎石应力依赖特性的路面结构分析，通过使用UMAT子程序定义沥青稳定碎石的材料特性. Abaqus有限元软件的应力、应变数值模拟流程如图 5所示.该软件使用基于单元位移和应变的有限元分析方法，应力通过应变和材料的本构方程计算得出，应力和应变之间的关系由材料的本构模型定义.因此，在编写UMAT材料特性子程序时，需要把材料的应力依赖特性转化为应变依赖特性.

通过分析研究发现回弹模量应力依赖特性的应变表达可分为显示和隐式两类，表达类型取决于回弹模量应力依赖模型的选取，具体分析过程如下.

首先，通过胡可定理将体应力和八面体剪应力转换为应变的表达式，即

$\theta = \frac{{ - MR}}{{\left( {1 - 2\nu } \right)}}({\varepsilon _{11}} + {\varepsilon _{22}} + {\varepsilon _{33}}),$

(1)

$\begin{array}{l} {\tau _{{\rm{oct}}}} = \frac{{{M_R}}}{{3\left( {1 + \nu } \right)}}\left[ {{{({\varepsilon _{11}} - {\varepsilon _{22}})}^2} + {{({\varepsilon _{11}} - {\varepsilon _{33}})}^2} + ({\varepsilon _{22}} - } \right.\\ {\left. {\quad \quad {\varepsilon _{33}}{)^2} + {{\left( {\frac{{{\varepsilon _{12}}}}{2}} \right)}^2} + {{\left( {\frac{{{\varepsilon _{13}}}}{2}} \right)}^2} + {{\left( {\frac{{{\varepsilon _{23}}}}{2}} \right)}^2}} \right]^{ - 1/2}}. \end{array}$

(2)

式中：M_R为回弹模量, q为体应力, s₁+s₂+s₃，t_oct为八面体剪切应力，1/3[(s₁-s₂)²+(s₁-s₃)²+(s₂-s₃)²]^1/2，e_ij为应变分量，n为泊松比.之后将式(1)、(2) 代入回弹模量应力依赖模型，得到应力依赖模型的应变表达式.具体表达形式取决于模型的选取.当采用Universal Soil Model时，可解得模型的显式应变表达为

${M_R} = Pa{\left( {{k_1}{{\left( A \right)}^{{k_2}}}{{\left( B \right)}^{{k_3}}}} \right)^{\frac{1}{{1 - {k_2} - {k_3}}}}}.$

式中：$A = \frac{{ - ({\varepsilon _{11}} + {\varepsilon _{22}} + {\varepsilon _3})}}{{\left( {1 - 2v} \right)}}$, $B = {\left[ {{{({\varepsilon _{11}} - {\varepsilon _{22}})}^2} + {{({\varepsilon _{11}} - {\varepsilon _{33}})}^2} + {{({\varepsilon _{22}} - {\varepsilon _{33}})}^2} + {{\left( {\frac{{{\varepsilon _{12}}}}{2}} \right)}^2} + {{\left( {\frac{{{\varepsilon _{13}}}}{2}} \right)}^2} + {{\left( {\frac{{{\varepsilon _{23}}}}{2}} \right)}^2}} \right]^{ - 1/2}}/3\left( {1 + v} \right)$, P_a为大气压，k₁, k₂, k₃为材料回归常数.

然而，当采用MEPDG模型时，只能得到模型的隐式应变表达，必须通过迭代法求解.迭代方式和收敛标准分别为

$\begin{array}{l} {M_{R(n)}} = {K_1}Pa{\left( {\frac{{A \cdot {M_{R(n - 1)}}}}{{Pa}}} \right)^{{K_2}}}{\left( {\frac{{B \cdot {M_{R(n - 1)}}}}{{Pa}} + 1} \right)^{{K_3}}},\\ \quad \quad \quad \quad \left| {{M_{R(n)}} - {M_{R(n - 1)}}} \right| \le D. \end{array}$

式中：M_R(n)为当前迭代步数下的回弹模量, M_R(n-1)为前一次迭代步数下的回弹模量，D为收敛标准.

此外，Abaqus要求在UMAT子程序中定义雅克比矩阵C=∂S/∂E，其中C为材料的雅克比矩阵，E为应变张量，S为应力张量.当模量模型为显式应变表达时，可以通过求导直接计算出雅克比矩阵，而使用隐式表达时只能通过C≈ΔS/ΔE近似表达^[18].本研究采用MEPDG模型，因此通过C≈ΔS/ΔE近似计算雅克比矩阵.有限元分析过程中，可能出现ΔE分量为0的节点，从而导致奇点(singularity)出现；此时，采用该节点割线劲度矩阵中的对应相近似雅克比矩阵中的数值.需要指出：依据Abaqus计算手册，UMAT子程序分别计算应力和雅克比行列式，近似计算的雅克比行列式只会影响迭代的收敛速度，而不会影响计算精度.

4 应力依赖特性的本构模型有限元验证

为了验证用户自定义UMAT材料模块的准确性和稳定性，研究首先通过两个简单有限元模型对子程序进行验证.第1个验证模型为三轴实验模拟，用来验证子程序的准确性；第2个验证模型为简支梁，用来验证程序的稳定性.

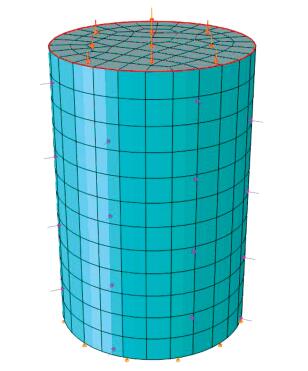
三轴实验模拟完全依照室内试验的实际情况建立有限元模型(图 6).首先建立试件的三维模型(直径10 cm，高度15 cm)，用户定义材料参数(k₁、k₂和k₃)选用沥青质量分数为3.5%的沥青稳定碎石的测试回归参数，假定泊松比为0.5.材料下部固定，与实验过程相对应施加15组荷载组合.模拟过程中，试件的回弹模量直接由UMAT子程序算出并输出到指定文件.

研究通过对比模拟计算得到的材料模量和试验测得回弹模量来验证模型的准确性. 图 7中，横坐标为实测模量M，纵坐标为模拟模量S，15个数据点对应15组应力加载状态.数据点沿等值线两侧分布，表明模拟数据和实测数据相吻合.模拟数据和实测数据之间的差别主要由MEPDG回弹模量模型参数回归的误差导致.验证结果表明通过UMAT子程序实现的用户定义材料能够表征沥青稳定碎石回弹模量的应力依赖特性.

此外，研究通过简支梁模拟UMAT子程序的稳定性. MEPDG回弹模量模型的表达形式中，体应力的数值必须为正数.然而，路面结构的沥青层底部可能产生较大水平拉应力，导致体应力为负数(研究使用土力学系统对应力方向的定义：拉应力为负，压应力为正)，从而使数值模拟出现错误或计算不收敛.为避免这一情况，研究在UMAT子程序中规定了体应力的最小值，当节点的实际计算结果小于该阈值时，子程序使用该最小值为节点的体应力.简支梁底部和沥青层底部的受力状态相近.模拟结果显示，对于底部收拉的情况，UMAT子程序的计算结构收敛，稳定性满足要求. 图 8显示了简支梁中回弹模量的分布.在支座和顶部受压区域，材料的模量值较高，底部收拉区域的模量较低.

5 基于回弹模量应力依赖特性的路面结构分析

基于UMAT子程序定义的用户材料，进行基于回弹模量应力依赖特性的有限元路面结构分析，并与线弹性路面结构分析相比较.研究选取的路面结构层的材料类型，厚度和材料特性见表 2.

应力依赖非线性路面结构分析中只考虑沥青稳定碎石的非线性依赖特性，其材料参数使用表 1中对应不同沥青含量的MEPDG模型参数；对于线弹性路面结构分析，沥青稳定碎石的回弹模量通过FWD实验结果反算得到，但所测路面结构中的沥青稳定碎石只有4%一种沥青质量分数.

路面结构应力、应变分析是力学-经验路面设计方法的基础.分析结果中选取的力学参数需要针对路面结构破坏形式，并且常被用来评价和预测路面的使用性能.基于国外研究已取得的成果和我国现行的路面设计规范，研究选取了面层底部拉应变、基层底部拉应变、垫层顶部竖向压应力和路基顶部竖竖向应力.然而，在双圆均布轮载下，所选定的力学参数数值大小沿道路横断面方向发生变化.通常最不利荷载位置位于轮胎中心下方至双轮中心下方之间的区域.为确定非线性应力依赖路面结构分析中每种参数的最不利位置，数据分析过程中读取了FEM输出数据库中各选定参数在固定深度沿道路横断面方向不同节点的数据. 图 9显示了各力学参数沿道路横断面方向的分布.图中横坐标表示数据读取节点与双轮中心的水平距离，阴影区域表示在轮胎下方的区域.面层底部压应变在轮胎下方达到最大值，且分布较均匀，因此取轮胎中心下为最不利位置.基层底部拉应变和垫层顶部压应力在轮胎中心线下偏内侧区域达到最大值；路基顶部的竖向压力在双轮中心达到最大值.

研究比较了非线性应力依赖路面结构分析和线弹性路面结构分析结果的差异. 图 10中，虚线表示采用MEPDG模型的非线性应力依赖路面结构分析结果，圆点表示采用FWD反算回弹模量的线弹性分析结果.图中可以看出，由于采用了沥青稳定碎石，面层底部的拉应变数值较小，且非线性线模拟和线性模拟的结果很接近.对于路基顶面最大压应力，线性和非线性的计算结果比较接近.然而，与非线性分析相比，弹性分析低估了沥青稳定碎石基层底部拉应变约10%，低估级配碎石顶部最大压应力约5%.沥青层底部拉应变被广泛用于预估沥青路面的疲劳寿命，根据MEPDG的预估模型^[21]，低估10%的层底拉应变将导致高估40%的疲劳寿命.需要指出的是, 分析只考虑了沥青稳定碎石的分线性依赖特性.路基土，继配碎石和沥青混凝土都具有不同程度的应力依赖特性.若考虑所有材料的非线性应力依赖特性，这一差异将进一步扩大.材料的非线性应力依赖特性显著影响路面分析结果，应在路面结构设计时考虑其模量的非线性应力依赖特性.

6 结论

1) 采用动三轴试验模拟不同应力状态，测试沥青稳定碎石的回弹模量，建立材料的非线性应力依赖本构模型，进一步编程并定义沥青稳定碎石的本构模型并采用Abaqus有限元软件进行基于沥青稳定碎石非线性应力依赖本构模型的路面结构数值模拟.

2) 沥青稳定碎石的回弹模量具有较强的应力依赖特性，回弹模量随体应力的增加而增加，随剪应力的增加而减小.在研究所涵盖的应力状态下，其模量最大值为最小值的175%.导致沥青稳定碎石模量应力依赖特性的原因是石料颗粒间的相互作用，具体作用方式见文中阐述.

3) 通过验证实验表明，编程并定义的沥青碎石本构模型能够准确地反映材料的模量的非线性应力依赖特性.通过有限元路面结构分析可知，与非线性分析相比，弹性分析低估了沥青稳定碎石基层底部拉应变约10%，低估级配碎石顶部最大压应力约5%.沥青稳定碎石的非线性应力依赖特性显著影响路面分析结果，应在路面结构设计时考虑其模量的非线性应力依赖特性.