氯离子侵蚀引起的钢筋混凝土结构抗力及耐久性下降的问题逐渐成为研究热点[1-3].在结构抗力研究中,锈蚀钢筋截面面积计算模型主要采用均匀锈蚀模型和点蚀模型[4-5],并未综合考虑均匀锈蚀和坑蚀两种状态同时发生时对钢筋截面面积变化的影响.同时,关于裂缝影响的研究大多集中于建立裂缝宽度或钢筋锈蚀率的联系,如文献[6]对钢筋开裂后的锈蚀产物体积进行计算,基于修正后的裂缝宽度计算模型,得到混凝土开裂后钢筋的锈蚀率;文献[7]基于45片RC构件腐蚀试验结果,建立了锈胀开裂宽度的预测模型,并对各参数进行敏感性分析.很少有学者在理论上建立锈胀裂缝与结构抗力的联系.以往钢筋混凝土结构可靠度的研究大多假定材料性能及结构参数在空间上分布均匀,只考虑材料参数的时变性和不确定性,不考虑各参数的空间变异性对结构性能退化的影响.但实际结构中,不同位置的材料性能和结构尺寸可能存在差异,最后造成结构的安全评价偏向保守.随着可靠度研究的深入,考虑参数的空间变异性对结构可靠度的研究越来越迫切.目前,有极少数学者对结构的空间变异性展开研究.文献[8]基于混凝土抗压强度、表面氯离子浓度质量和保护层厚度三者的空间变异性,建立一维时空模型,并对钢筋混凝土结构的承载能力和锈胀开裂损伤进行系统的分析,同时针对性的提出相关维护方法;文献[9]综合考虑多种参数的空间变异性,研究了氯离子侵蚀环境下结构的开裂比例;文献[10]基于氯离子扩散试验数据得到氯离子扩散系数计算模型,通过引入参数空间变异性,建立RC结构初始锈蚀模型.然而以上学者并未考虑同一RC梁中不同受拉主筋锈蚀不均衡以及裂缝对RC梁抗力的影响.
因此本文以RC梁加速锈蚀试验为基础,首先综合考虑均匀锈蚀和点蚀的影响,得到改进的钢筋截面面积时变模型;随后考虑裂缝的影响,建立裂缝宽度与氯离子扩散系数和RC梁结构抗力的关系;其次,通过引入失效模式特征系数k和锈蚀不平衡系数ψ,得到包含nm根锈蚀不均匀主筋的RC梁的抗力计算公式;最后基于随机场理论,建立考虑材料性能和结构尺寸空间变异性时RC梁的抗力时空退化模型.
1 RC梁抗力时空退化模型 1.1 钢筋截面面积时变改进模型在实际锈蚀中,由于材料和环境的不确定性,钢筋很少单独发生均匀锈蚀或者坑蚀,往往两种锈蚀状态同时发生,然而这两种锈蚀状态均会导致钢筋截面面积的损失.本文综合考虑以上两种锈蚀状态的影响,得到截面面积计算公式为
| $ A\left( t \right) = {M_1}{A_{{\rm{pit}}}}\left( t \right) + {M_2}{A_{{\rm{uni}}}}\left( t \right). $ | (1) |
式中:M1、M2分别为坑蚀和均匀锈蚀两种锈蚀状态发生的权重,M2=1-M1;Apit(t)和Auni(t)分别为钢筋在坑蚀和均匀锈蚀下的剩余截面面积.
运用文献[11]中的面积损失计算公式得到钢筋发生坑蚀时的截面面积损失,从而参数M1可由坑蚀造成的实际截面面积损失和理论截面面积损失的比值表示为
| ${M_1} = \frac{{{A_{{\rm{pit}}}}}}{{{A_{{\rm{pit}}}}\left( t \right)}} = \frac{{{A_{{\rm{pit}}}}}}{{{A_{{\rm{pit}}}} + \frac{{2\alpha }}{{2{\rm{ \mathsf{ π} }}}}{A_{{\rm{uni}}}}}} = \frac{{{A_{{\rm{pit}}}}}}{{{A_{{\rm{pit}}}} + {{\rm{ \mathsf{ π} }}^{ - 1}}{A_{{\rm{uni}}}}\arcsin {{\frac{{{b_{{\rm{pit}}}}}}{{{D_0}}}}^{ - 1}}}}.$ | (2) |
式中:Auni可近似于均匀锈蚀在钢筋截面边缘的非光滑区域引起的面积损失,Apit为除上述区域外由蚀坑影响引起的面积损失,bpit为蚀坑宽度,D0为钢筋初始直径.
本文基于实验所测数据及式(2) 计算参数M1,部分结果如表 1所示.对参数M1进行统计分析发现:1) 当最大截面损失率C<9.5%时,M1服从均值为0.32、标准差为0.076的正态分布;2) 当C≥9.5%时,M1服从均值为0.65、标准差为0.078的正态分布.对上述正态分布进行K-S检验和S-W检验:当C<9.5%时,K-S检验和S-W检验的结果分别为0.192和0.717;当C≥9.5%时,K-S检验和S-W检验的结果分别为0.137和0.311.以上结果表明:当显著性水平α=0.05时,参数M1服从正态分布.
| 表 1 参数M1(部分数据) Table 1 Parameter M1 (partial data) |
目前,相关研究表明钢筋屈服强度fy的退化与截面面积损失可近似为线性相关[12-14],即
| $ {f_{\rm{y}}}\left( t \right) = \left[ {1 - \left( {{\alpha _{\rm{y}}}\frac{{\Delta {A_{st}}\left( t \right)}}{{{A_0}}} \times 100} \right)} \right]{f_{{\rm{y0}}}}. $ | (3) |
式中:ΔAst(t)为锈蚀引起的钢筋截面面积损失,由式(1) 推导可得;A0、fy0分别为钢筋初始的截面面积和屈服强度;αy为经验系数,由于实验测试环境不同,国内外学者对αy的取值存在不同的意见,文献[15]认为αy的值为0.017,而一些学者将αy取值为0.005,本文对实测的锈蚀钢筋屈服强度进行统计分析,得到αy的平均值为0.003 5.
1.3 考虑裂缝的影响在服役过程中,混凝土结构的开裂会导致混凝土强度降低,同时也会加快氯离子对结构的侵蚀,导致结构承载力下降.而结构承载力的下降会进一步导致混凝土开裂,最终导致结构承载力大幅降低.
裂缝的存在为氯离子和其他物质到达钢筋提供了最优路线,加速了锈蚀.尽管氯离子扩散特性受到裂缝宽度、温度、湿度和表面氯离子质量浓度变化等影响,但在实际结构中,由于裂缝宽度较易获得,且其与氯离子扩散系数存在明显的联系,故本文只考虑裂缝宽度w对氯离子侵蚀的影响.文献[16]对服役8 a和11 a的钢筋混凝土结构早期锈胀裂缝研究,得到了不同裂缝宽度对应的平均氯离子扩散系数D(w)和表面氯离子质量浓度,通过引入裂缝影响函数f(w)对开裂混凝土中氯离子的侵蚀行为描述为
| $ \left\{ \begin{array}{l} D\left( w \right) = f\left( w \right)D,\\ f\left( w \right) = \left( {31.61{w^2} + 4.73w + 1} \right). \end{array} \right. $ | (4) |
式中D为非开裂混凝土中氯离子扩散系数,w≥0.1 mm.
当不考虑裂缝影响时,结构服役过程中的混凝土强度fc′可认为与初始混凝土强度fc相同;当考虑裂缝影响时,混凝土强度fc′具有时变性.本文基于锈蚀速度和裂缝宽度,采用文献[17]建立的模型计算混凝土强度的降低值,从而得到任一时刻的混凝土强度fc′为
| $f_{\rm{c}}^{'} = {f_{\rm{c}}} - \Delta {f_{\rm{c}}} = {f_{\rm{c}}} - \frac{{{f_{\rm{c}}}}}{{1 + K\frac{{{\varepsilon _1}}}{{{\varepsilon _{{\rm{c}}0}}}}}}.$ | (5) |
式中:Δfc为混凝土强度降低值,fc为初始混凝土强度,K是与钢筋粗糙度和直径相关的系数,文献[18]认为当结构中的钢筋为带肋钢筋时,K=0.1,ε1、εc0分别为开裂混凝土在直角方向上的压应力峰值和平均拉伸应力,ε1的计算公式为
| $ {\varepsilon _1} = \frac{{{b_{\rm{f}}} - {b_0}}}{{{b_0}}}. $ | (6) |
式中bf、b0分别为锈胀裂缝增加的宽度和初始状态的截面宽度,bf与b0之差[19]为
| $\begin{array}{*{20}{l}} {{b_{\rm{f}}} - {b_0} = {n_{{\rm{bars}}}}w = }\\ {\;\;{n_{{\rm{bars}}}}\left[ {\frac{{4{\rm{ \mathsf{ π} }}{d_{\rm{s}}}\left( t \right)}}{{\frac{{1 - {\nu _{\rm{c}}}}}{{{{\left( {\frac{{{d_1}}}{{{d_2}}}} \right)}^{\sqrt \alpha }}}} + \frac{{1 + {\nu _{\rm{c}}}}}{{{{\left( {\frac{{{d_2}}}{{{d_1}}}} \right)}^{\sqrt \alpha }}}} - \frac{{2{\rm{ \mathsf{ π} }}{d_2}{f_t}}}{{{E_{{\rm{ef}}}}}}}}} \right].} \end{array}$ | (7) |
式中:nbars为受压钢筋的数量,w为裂缝宽度, 可由上式计算,νc为混凝土的泊松比,α为切向刚度折减系数,具体计算方法见文献[19],ft为混凝土的抗拉强度,Eef为混凝土的有效弹性模量,d1、d2分别为厚壁圆柱的内、外半径,且d1=(D0+2d0)/2, d2=S/2, D0为钢筋初始直径,d0为混凝土空隙的环形层厚度,S为钢筋间距,ds(t)为腐蚀产物形成的厚度,计算公式[20]为
| $ {d_{\rm{s}}}\left( t \right) = \frac{{{W_{{\rm{rust}}}}\left( t \right)}}{{{\rm{ \mathsf{ π} }}\left( {{D_0} + 2{d_0}} \right)}}\left( {\frac{1}{{{\rho _{{\rm{rust}}}}}} - \frac{{{\alpha _{{\rm{rust}}}}}}{{{\rho _{{\rm{st}}}}}}} \right). $ | (8) |
式中:αrust为与生锈类型相关的系数;ρrust、ρst分别为铁锈和钢筋的密度;Wrust为单位长度的钢筋锈蚀量,计算式[20]为
| $ {W_{{\rm{rust}}}}\left( t \right) = {\left[ {2\int_0^t {0.105\left( {1/{\alpha _{{\rm{rust}}}}} \right){\rm{ \mathsf{ π} }}{D_0}{i_{{\rm{corr}}}}\left( t \right){\rm{d}}t} } \right]^{1/2}}. $ | (9) |
为得到更为精准的结构抗力退化模型,本文将混凝土抗压强度、保护层厚度、表面氯离子质量浓度和临界氯离子质量浓度视为空间随机变量,将钢筋混凝土结构离散成N个立体单元,运用一维随机场理论对整个RC梁的抗力退化进行研究.随机场的分析主要有以下4种方法:1) 中点法;2) 形函数法;3) 空间均值法;4) Karhunen-Loeve分解法.由于实际结构中的材料性能、荷载和抗力等参数并非全部服从高斯分布,而中点法对于高斯分布和非高斯分布均适用,同时以任意单元质心处的参数值代表该参数在该单元的分布值可大大简化计算,故本文采用中点法进行随机场分析.关于中点法的介绍见文献[21].
1.4.1 研究假定条件本文采用离散梁单元的方法对RC梁各参数的空间变异性进行研究,所示算例的单元划分如图 1所示.基于划分得到的N个梁单元作如下假定:1) 对N个梁单元进行研究时,采用的退化模型和材料参数的分布形态具有一致性;2) 各个梁单元已经充分小,不再考虑各参数在单元内部不同位置处的空间变异性.
1.4.2 自相关函数随机场分析的关键在于选取合适的自相关函数对各单元参数的空间变异性进行描述.两相关单元的距离越小,自相关函数越大,反之越小.目前,不同的随机领域存在不同的自相关函数,如三角函数、高斯函数、矩形函数等,而高斯(平方指数)相关函数在工程实际研究中得到广泛运用,因此,本文采用一维高斯函数作为自相关函数,即
| $ {\rho _{\rm{G}}}\left( \varepsilon \right) = \exp \left[ { - \left( {\frac{{{{\left| {{\varepsilon _x}} \right|}^2}}}{{d_x^2}}} \right)} \right]. $ | (10) |
式中:εx=xi-xj为两相关单元i和j的质心在x方向上的距离,
在分析材料性能和结构尺寸的空间变异性时,一旦结构单元划分完毕,相关系数矩阵就随之被确定.假设结构被划分为N单元,则相关系数矩阵为
| $ \mathit{\boldsymbol{\rho }} = \left[ {\begin{array}{*{20}{c}} {{\rho _{11}}}&{{\rho _{12}}}& \cdots &{{\rho _{1n}}}\\ {{\rho _{21}}}&{{\rho _{21}}}& \cdots &{{\rho _{2n}}}\\ \cdots&\cdots&\cdots&\cdots \\ {{\rho _{n1}}}&{{\rho _{n2}}}& \cdots &{{\rho _{nn}}} \end{array}} \right]. $ | (11) |
式中ρij为单元i和单元j之间的相关系数,有
| $ \left\{ \begin{array}{l} 0 \le {\rho _{ij}} < 1;\\ \begin{array}{*{20}{c}} {{\rho _{ij}} = 1,i = j;}\\ {{\rho _{ij}} = {\rho _{ji}}.} \end{array} \end{array} \right. $ | (12) |
考虑锈蚀RC梁各单元之间参数的空间变异性时,各单元中钢筋的锈蚀速度、强度和材料性能退化值均不相同,从而每个单元中的极限承载能力也不尽相同.不考虑空间变异性时,单筋RC梁的极限弯曲能力Mu计算式[14]为
| $ {M_{\rm{u}}} = Q \times {E_{{\rm{bond}},i}} \times {A_{{\rm{st}},i}}\left( t \right){f_{{\rm{y}},i}}\left( t \right)\left( {{h_0} - \frac{{{A_{st,i}}\left( t \right){f_{{\rm{y}},i}}\left( t \right)}}{{1.7{{f'}_{\rm{c}}}b}}} \right). $ | (13) |
式中:Q为模型不确定系数,Ebond,i为第i个单元中钢筋和混凝土之间的粘结行为,具体见文献[14],b、ho分别为梁的宽度和有效高度,fc′为混凝土抗压强度.
然而在实际结构中,RC梁底部一般包含多根(nm)受拉主筋,且由试验分析可知,同一RC梁中各受拉主筋的锈蚀程度存在较大差异,则nm根钢筋的抗力也随之不同.假设nm根钢筋中锈蚀程度最小的钢筋截面损失率为ρ0,将其余钢筋的锈蚀程度用ρ0表示,则梁中nm根受拉主筋的锈蚀程度从小到大排列为
| $ \left\{ {{\rho _0},{\rho _1},{\rho _2}, \cdots ,{\rho _{m - 1}}} \right\} = \left\{ {{\rho _0},{B_1}{\rho _0},{B_2}{\rho _0}, \cdots ,{B_{m - 1}}{\rho _0}} \right\}. $ | (14) |
同时定义极限损失量Mlimit和nm根受拉主筋的最大锈蚀率max{ρi}与ρ0的比值分别为失效模式特征系数k和锈蚀不均衡系数ψ,具体表示为
| $ k = \frac{{{M_{{\rm{limit}}}}}}{{{\rho _0}}}, $ | (15) |
| $ \psi = \frac{{\max \left\{ {{\rho _i}} \right\}}}{{{\rho _0}}} = \frac{{{\rho _{m - 1}}}}{{{\rho _0}}} = {B_{m - 1}}. $ | (16) |
则RC梁中nm根钢筋的失效模式及结构抗力可分为以下几种情况.
1) 当ρi ≥Mlimit,即k≤1时,全部的受拉主筋均发生脆性失效,此时RC梁抗力为[14]
| $ {r_1}\left( t \right) \le {r_2}\left( t \right) \le {r_{{n_m}}}\left( t \right). $ | (17) |
式中:r1(t)≤r2(t)≤……rnm(t),ri(t)=fy, i(t)Ast, i(t),fy, i(t)、Ast, i(t)分别为编号为i的钢筋在时刻t时的剩余强度和截面面积.
2) 当ρi<Mlimit,即ψ=Bm-1<k时,全部的受拉主筋均发生延性失效,此时RC梁抗力为[14]
| ${M_{{\rm{u}},{\rm{total}}}}\left( t \right) = \frac{{{r_{{\rm{total}}}}\left( t \right)}}{{{n_m}{f_{{\rm{yo}}}}{A_0}}}{M_u} = \frac{{\sum\limits_{i = 1}^{{n_m}} {{r_i}\left( t \right)} }}{{{n_m}{f_{{\rm{yo}}}}{A_0}}}{M_{\rm{u}}}.$ | (18) |
3) 当ρ0<Mlimit<ρm-1,即1<k<ψ=Bm-1时,在全部受拉主筋组成的钢筋系统中,有P{1<Bi<k│1≤i≤m-1}的钢筋发生延性失效,P{k ≤ Bi<Bm-1│1≤i≤m-1}的钢筋发生脆性失效,此时RC梁的抗力可等价于两个子系统的抗力组合而成.
| $\begin{array}{*{20}{c}} {{M_{{\rm{u}},{\rm{total}}}}\left( t \right) = \frac{{{r_{{\rm{system1}}}}\left( t \right) + {r_{{\rm{system2}}}}\left( t \right)}}{{{n_m}{f_{{\rm{yo}}}}{A_0}}}{M_{\rm{u}}} = }\\ {\frac{{\sum\limits_{i = 1}^{{n_m} - L} {{r_i}\left( t \right)} + \max \left\{ {L{r_{{n_m} - L + 1}}\left( t \right),\left( {L - 1} \right){r_{{n_m} - L + 2}}\left( t \right), \cdots \cdots ,2{r_{{n_m} - 1}}\left( t \right),{r_{{n_m}}}\left( t \right)} \right\}}}{{{n_m}{f_{{\rm{yo}}}}{A_0}}}{M_{\rm{u}}}.} \end{array}$ | (19) |
式中L为集合{k≤Bi<Bm-1}中元素的个数.
考虑结构参数的空间变异性时,RC梁抗力的退化分析包含大量随机参数,如结构材料、保护层厚度和锈蚀钢筋的力学性能等,这些随机变量均具有时间和空间变化的分布特征和退化过程,具体计算过程十分复杂且难以推导其闭合解.因此,本文使用Monte-Carlo模拟的方法分析结构抗力的退化.只要随机场单元确定,就能基于各单元之间的自相关函数,得到各参数的空间随机变量,继而预测RC梁的抗力退化.基于Monte-Carlo模拟计算RC梁抗力时空退化的步骤:1) 基于随机场理论,将结构离散为多个空间单元,明确各单元内所需考虑的随机变量;2) 选定合适的自相关函数模型,定义相关系数矩阵ρ; 3) 将定义的系数矩阵ρ进行Choleski分解得到一上三角矩阵S;4) 计算考虑裂缝影响时任意时刻的混凝土强度值;5) 基于上三角矩阵S及各单元初始随机变量值得到所需考虑的各材料性能和结构尺寸的空间随机分布矩阵;6) 综合考虑所有随机变量,对抗力退化模型进行多重循环计算,得到各单元力学性能及抗力退化,得到RC梁抗力时空退化曲线.
2 算例分析 2.1 RC结构选取一长度为12.5 m的RC简支梁,其截面b×h=250 mm×500 mm,结构底部为两根Φ22钢筋.选择单元尺寸时,若选取的单元个数越多,则计算结果越准确,但此时运算量极大,导致程序计算速度大大降低.综合考虑以上因素,本文取单元尺寸Δ=0.5 m对RC梁进行划分,得到25个立体单元,此时RC梁中的主筋也随之被离散,具体如图 1所示.
|
图 1 梁单元划分 Figure 1 Unit division |
其中,用于结构抗力计算的表面氯离子质量浓度(%)、临界氯离子质量浓度(%)和混凝土保护层厚度(mm)均服从正态分布,均值和方差分别为0.114和0.1, 0.042和0.108, 及29.8和0.07;模型不确定系数Q和腐蚀电流密度(μA/cm2)均服从对数正态分布,均值和方差分别为0.98和0.5, 及0.53和0.2;混凝土初始强度(MPa)服从均值为20.72和方差为0.177的正态分布;钢筋初始屈服强度值为366 MPa.同时,对计算裂缝影响的相关变量进行如下取值:νc、ft、Eef、ρst、S分别取值为0.2 MPa、2.01 MPa、3.0×104MPa、7 800 kg/m3、190 mm,d0、ρrust、αrust的取值分别为12.5 μm、3 600 kg/m3、0.57[19].
本文假定各参数的变化均为平稳随机过程,考虑混凝土抗压强度、保护层厚度、表面氯离子质量浓度和临界氯离子质量浓度的空间变异性对结构抗力的影响,并对结构正常服役100 a后的抗力进行预测.在随机场分析中,选取波动系数θ=2.0 m来计算各单元之间的相关函数值.尽管文献[8]研究发现:当波动系数由1 m变化到3 m时,发生锈蚀破坏的概率并没有明显的变化,但波动系数对结构抗力的影响仍需进一步展开研究.
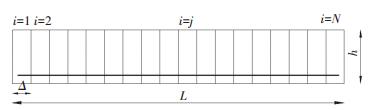
2.2 结果分析1) 锈蚀模型的影响.当结构位于海洋线大气环境下且考虑裂缝对抗力的影响时,基于改进后的面积计算模型、点蚀模型和均匀锈蚀模型3种面积计算模型,研究了不同锈蚀模型对RC梁抗力退化规律的影响.如图 2所示,不论采用哪种面积计算模型,RC梁的抗力均随时间t的增大而减小.当不考虑参数的空间变异性时,结构正常服役100 a后,采用本文改进的面积计算模型得到的抗力值较采用均匀锈蚀模型时低了5.60%,比采用点蚀模型时高3.12%;同时采用改进模型得到的抗力变化规律在服役前段更接近均匀锈蚀模型,而服役后段更靠近点蚀模型,这表明以往采用的点蚀模型低估了结构的抗力,改进的模型更好地反应RC梁锈蚀状态.当考虑相关参数空间变异性时,以上3种面积计算模型对应的RC梁的抗力值比不考虑各参数空间变异性时分别下降了14.68%、17.84%、14.13%,且初锈时间较不考虑各参数空间变异性时提高了9.28%.因此不考虑各参数的空间变异性将低估RC梁的抗力退化.

|
图 2 不同面积模型下抗力退化(Δ=0.5 m、θ=2.0 m) Figure 2 Resistance degradation under different area models(Δ=0.5 m, θ=2.0 m) |
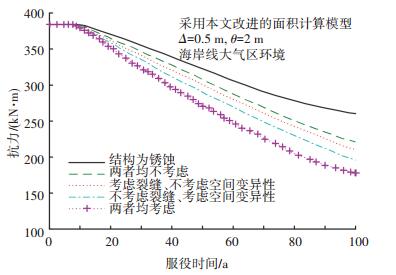
2) 裂缝的影响.图 3、4分别为裂缝与抗力退化关系图和不同裂缝宽度w对应的抗力退化图.由图 3可知,结构正常服役100 a后,在考虑各参数空间变异性的前提下,不考虑裂缝影响得到的抗力值比考虑裂缝影响的抗力值高9.91%;而不考虑各参数的空间变异性时,不考虑裂缝影响得到的抗力值比考虑裂缝影响的抗力值高5.75%.本文以沿海地区混凝土结构在正常使用条件下的最大允许裂缝宽度0.1 mm为基础,研究不同裂缝宽度对应的抗力退化:当考虑空间变异性且裂缝宽度为0.1、0.15、0.2、0.25 mm时,结构剩余抗力较不考虑裂缝影响时分别下降了2.41%、3.61%、4.60%、5.56%,且随着裂缝宽度的增大,增加相同裂缝宽度值对结构抗力的影响逐渐减小,钢筋初始锈蚀时间的提前幅度也随之减小.表明裂缝对结构正常服役行为影响较大,不考虑裂缝的影响会较大程度高估结构的剩余抗力.
|
图 3 裂缝与抗力退化图 Figure 3 Crack and resistance degradation |

|
图 4 不同裂缝宽度w对应的抗力 Figure 4 Different crack width w and resistance |
3) 随机场参数的影响.由图 5可知,结构正常服役100 a后,考虑结构各参数的空间变异性且波动系数θ取1、2、3 m时,结构抗力相比初始抗力分别下降51.57%、53.65%、55.47%.与波动系数取2 m时相比,波动系数为1 m时结构的初锈时间延缓了4.47%,而波动系数为3 m时结构的初锈时间却提前了4.91%.这说明适当的增加波动系数能够使结构的抗力进一步退化,但影响效果不显著.

|
图 5 波动系数θ与抗力退化 Figure 5 Fluctuation coefficient θ and resistance deterioration |
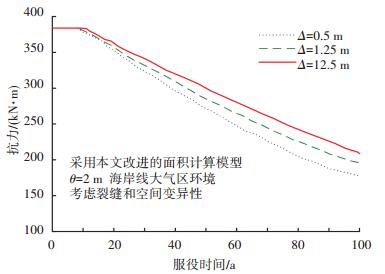
当单元尺寸Δ=12.5 m时,单元尺寸与结构的实际尺寸相同,此时可视为不考虑各参数的空间变异性对抗力的影响.由图 6可知,当考虑各参数的空间变异性时,RC梁的抗力随着单元尺寸划分的不同有较大的差异,其中在单元尺寸Δ=0.5、1.25 m两种情形下,RC梁的抗力比不考虑空间变异性的影响时分别下降了14.68%、9.62%.因此,当考虑结构各参数的空间变异性时,适当的选取单元尺寸对RC梁的安全评估十分重要.
|
图 6 单元尺寸Δ与抗力退化 Figure 6 Unit size and resistance degradation |
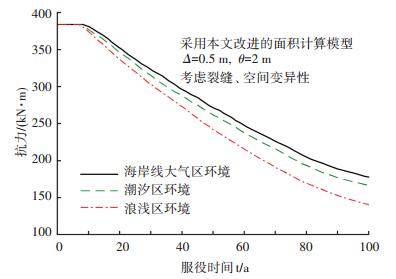
4) 环境参数的影响.在不同环境中,由于氯离子质量浓度和腐蚀电流密度的不同,RC结构的抗力退化规律也存在较大的差异. 图 7为RC结构在海岸线大气区、潮汐区和浪溅区3种环境下的抗力退化图.如图 7所示,不同环境对RC结构抗力退化的影响显著,在海岸线大气区环境下,结构正常服役100 a后,其剩余抗力值为初始结构抗力值的46.35%,而在潮汐区和浪溅区环境下结构剩余抗力分别为初始抗力值的43.23%和36.45%,比海岸线大气区环境下的对应值分别下降了6.73%和21.35%.结果表明以上3种环境中,浪溅区环境对结构抗力退化的影响最大,因此,在结构服役期间,要尽量做好防腐措施,减少氯离子侵蚀对结构耐久性的破坏.
|
图 7 不同环境下的抗力退化 Figure 7 Resistance degradation under different environments |
1) 以往计算钢筋截面面积的点蚀模型低估了结构的抗力,本文改进后的面积时变模型能更好的反应RC梁实际锈蚀状态.
2) 不考虑各参数的空间变异性和裂缝影响将较大程度上高估RC结构的抗力:当考虑各参数的空间变异性时,不考虑裂缝影响的抗力值比考虑裂缝影响时高9.91%,而不考虑各参数的空间变异性时,不考虑裂缝影响的抗力值比考虑裂缝影响时高5.75%,并且是否考虑各参数的空间变异性对预测RC梁的抗力值影响较大,两种情况得到的抗力值最大相差高达14.68%.
3) 适当地增加波动系数能够使结构的抗力进一步退化,但效果不显著;选取适当的单元尺寸对RC梁的安全评估十分重要;浪溅区环境对结构抗力退化的影响最大,要尽量做好防腐措施,减少氯离子侵蚀对结构耐久性的破坏.
| [1] |
马亚丽, 张爱林. 基于规定可靠指标的混凝土结构氯离子侵蚀耐久寿命预测[J].
土木工程学报, 2006, 39(2): 36-41.
MA Yali, ZHANG Ailin. Durablity life prediction of concrete structure based on the regulated reliability index under chloride environment[J]. China Civil Engineering Journal, 2006, 39(2): 36-41. DOI: 10.3321/j.issn:1000-131X.2006.02.008 |
| [2] |
刘文军, 王军强. 氯离子对钢筋混凝土结构的侵蚀分析[J].
混凝土, 2007, 27(4): 20-22.
LIU Wenjun, WANG Junqiang. Analysis of chloride ion diffusion in reinforced concrete structures[J]. Concrete, 2007, 27(4): 20-22. DOI: 10.3969/j.issn.1002-3550.2007.04.008 |
| [3] |
孙丛涛. 基于氯离子侵蚀的混凝土耐久性与寿命预测研究[D]. 西安: 西安建筑科技大学, 2011. DOI: 10.7666/d.d243557.
SUN Congtao. Study on concrete durability and service life prodiction based on chloride corrosion [D]. Xi'an: Xi'an University of Architecture and Technology, 2011. DOI:10.7666/d.d243557. http://cdmd.cnki.com.cn/Article/CDMD-10703-1011296488.htm |
| [4] |
张俊芝, 周巧萍, 伍亚玲, 等. 基于混凝土氯离子扩散系数时变性的钢筋坑蚀面积随机时变模型[J].
自然灾害学报, 2014, 23(2): 254-263.
ZHANG Junzhi, ZHOU Qiaoping, WU Yaling, et al. A random time-varying model of corrosion pit area of steel bars based on the time variability of chloride ion diffusion coefficient in concrete[J]. Journal of Natural Disasters, 2014, 23(2): 254-263. DOI: 10.13577/j.jnd.2014.0232 |
| [5] |
王磊, 马亚飞, 张建仁. 模糊及随机信息下桥梁构件抗力演化特征分析[J].
土木工程学报, 2013, 46(1): 76-83.
WANG Lei, MA Yafei, ZHANG Jianren. Analysis for evolutionary characteristics of resistance degradation of bridge members under fuzzy and random information[J]. China Civil Engineering Journal, 2013, 46(1): 76-83. DOI: 10.15951/j.tmgcxb.2013.01.005 |
| [6] |
吴锋, 张章, 龚景海. 基于锈胀裂缝的锈蚀梁钢筋锈蚀率计算[J].
建筑结构学报, 2013, 34(10): 144-150.
WU Feng, ZHANG Zhang, GONG Jinghai. Calculation of steel corrosion rate based on corrosive crack of beams[J]. Journal of Building Structures, 2013, 34(10): 144-150. DOI: 10.14006/j.jzjgxb.2013.10.017 |
| [7] |
彭建新, 胡守旺, 张建仁, 等. 钢筋混凝土结构锈胀开裂宽度的试验研究及预测模型[J].
实验力学, 2014, 29(1): 33-41.
PENG Jianxin, HU Shouwang, ZHANG Jianren, et al. Experimental study and prediction model of corrosion-induced crack width in RC structure[J]. Journal of Experimental Mechanics, 2014, 29(1): 33-41. DOI: 10.7520/1001-4888-13-003 |
| [8] |
STEWART M G, MULLARD J A. Spatial time-dependent reliability analysis of corrosion damage and the timing of first repair for RC structures[J].
Engineering Structures, 2007, 29(7): 1457-1464.
DOI: 10.1016/j.engstruct.2006.09.004 |
| [9] |
VU K A, STEWART M G. Predicting the likelihood and extent of reinforced concrete corrosion-induced cracking[J].
Journal of Structural Engineering, 2005, 131(11): 1681-1689.
DOI: 10.1061/(ASCE)0733-9445 |
| [10] |
彭建新, 胡守旺, 张建仁. 考虑温室效应的氯盐环境下RC桥梁锈胀开裂性能预测[J].
工程力学, 2013, 30(8): 103-110.
PENG Jianxin, HU Shouwang, ZHANG Jianren. Corrosion-induced crack performance prediction of rc bridge under chloride attack considering effect of global warming[J]. Engineering Mechanics, 2013, 30(8): 103-110. DOI: 10.6052/j.issn.1000-4750.2012.04.0261 |
| [11] |
彭建新, 阳逸鸣, 张建仁. 锈蚀钢筋截面面积分析及强度概率模型[J].
中外公路, 2015, 35(5): 124-129.
PENG Jianxin, YANG Yiming, ZHANG Jianren. Probabilistic cross-sectional area and strength model of corroded steel bar[J]. Journal of China and Foreign Highway, 2015, 35(5): 124-129. DOI: 10.14048/j.issn.1671-2579.2015.05.028 |
| [12] |
STEWART M G. Mechanical behaviour of pitting corrosion of flexu-ral and shear reinforcement and its effect on structural reliability of corroding RC beams[J].
Structural Safety, 2009, 31(1): 19-30.
DOI: 10.1016/j.strusafe.2007.12.001 |
| [13] |
MAYafei, ZHANG Jianren, WANG Lei, et al. Probabilistic prediction with Bayesian updating for strength degradation of RC bridge beams[J].
Structural Safety, 2013, 44(2334): 102-109.
DOI: 10.1016/j.strusafe.2013.07.006 |
| [14] |
彭建新, 张建仁, 张克波, 等. 锈蚀RC桥梁弯曲抗力时变概率模型与试验研究[J].
工程力学, 2012, 29(6): 125-132.
PENG Jianxin, ZHANG Jianren, ZHANG Kebo, et al. Probabilistic resistance model and experimental investigation for corroded RC bridges[J]. Engineering Mechanics, 2012, 29(6): 125-132. DOI: 10.6052/j.issn.1000-4750.2010.08.0614 |
| [15] |
DU Y G, CLARK L A, CHAN A H C. Residual capacity of corroded reinforcing bars[J].
Magazine of Concrete Research, 2005, 57(3): 135-147.
DOI: 10.1680/macr.2005.57.3.135 |
| [16] |
KWON S J, NA U J, PARK S S, et al. Service life prediction of concrete wharves with early-aged crack: probabilistic approach for chloride diffusion[J].
Structure Safety, 2009, 31(1): 75-83.
DOI: 10.1016/j.strusafe.2008.03.004 |
| [17] |
VECCHIO F, COLLINS M P. The modified compression field theory for reinforced concrete elements subjected to shear[J].
Proc ACI Structures, 1986, 83(2): 219-231.
|
| [18] |
CAPE M. Residual service-life assessment of existing RC structures [D]. Goteborg:Chalmers University of Technology, 1999.
|
| [19] |
LI C Q, ZHENG J J, LAWANWISUT W, et al. Concrete delamination caused by steel reinforcement corrosion[J].
ASCE Mater Civil Eng, 2007, 19(7): 591-600.
DOI: 10.1061/(ASCE)0899-1561(2007)19:7(591) |
| [20] |
LIU Y, WEYERS R E. Modelling the time-to-corrosion cracking in chloride contaminated reinforced concrete structures[J].
ACI Mater J, 1998, 95(6): 675-81.
|
| [21] |
VANMARCKE E H.
Random field: analysis and synthesis[M]. London: The MIT Press, 1983.
|
 2017, Vol. 49
2017, Vol. 49


