离散元法数值试验相较于物理试验,具有高效、便利、不确定性小、试验参数可控等特性,便于人们剖析试验机理,解释物理现象.周健等[1-6]研究了饱和层状砂土液化的特性,通过PFC2D研究了砂土颗粒与土工合成材料的接触界面,对砂土的双轴试验、力学性质、渗流过程以砂土中单桩进行了模拟.李识博等[7]通过颗粒流软件对黄土三轴固结不排水剪切试验进行了数值模拟.姜景山等[8]认为密度和围压是影响粗粒土三轴试验应力应变曲线的重要因素.徐小敏等[9]对颗粒材料初始杨氏模量、初始泊松比与颗粒法向刚度、颗粒刚度比的关系进行了研究,认为砂土材料的刚度比适宜取值范围为2.0~20.7.邢纪波等[10]推导出了单元接触刚度的计算公式,认为泊松比从0变到0.4时,颗粒刚度比对应范围为2.0~6.0.张振南等[11]提出了VMIB模型,建立起虚拟键力学属性与材料宏观力学响应的联系.蒋明镜等[12]在模拟砂土双轴试验时刚度比采用了1.33.周博等[13]认为颗粒破碎对砂土的宏观力学特性有很大的影响,其在模拟砂土双轴试验采用了刚度比为1的平行黏结模型.李宁等[14]通过PFC建立了三轴试验模型,模拟了砂土的三轴试验.离散元法中细观参数的取值决定了土样力学性质的宏观响应,目前众多学者提出了种类繁多的细观参数选取机制,但大都适用性不强,模拟的结果与实际相差较大.对于细观参数与宏观参数的标定仍然是一个值得探讨的问题.基于室内砂土三轴试验,利用PFC3D软件进行数值模拟,然后通过该试验介绍基于迭代思想标定宏-细观参数的方法,并且通过将本文的模拟结果与室内试验结果进行对比,来验证迭代标定法的有效性.迭代标定法提高了标定工作效率,可设置迭代终止准则,误差率可控,对于完成宏细观参数标定工作有重要的指导意义.
1 运用迭代法标定宏-细观参数 1.1 室内试验与数值模拟试验介绍室内粗粒土三轴试验试样是高8 cm,上下底面直径为4 cm的圆柱体.松散土的天然密度为1.39 g/cm3,室内试验土样密度为1.88 g/cm3,数值模拟试验中颗粒密度均为1.88 g/cm3.采用各向等压固结排水(CD)剪切的试验方法,试验采用应变控制,以轴向应变速率0.03 mm/min进行剪切,分别进行围压为50、100、150 kPa的3组试验,当试样的轴向应变达到15%时视为试样破坏.室内试验土样的颗粒级配:粒组划分为5~2、2~0.5、0.5~0.25、0.25~0.075、0.075~0.005、0.005~0 mm,土样质量分数分别为5.3%、20.4%、35%、26.6%、9.3%、3.4%.
为尽量与室内试验结果相近,在PFC3D中生成高为80 mm,上下底面直径均为40 mm的圆柱体模型,由于室内试验的土样粒径在0.075 ~2 mm之间占了82%,又考虑到生成太多颗粒会严重影响计算机运行速度,所以数值模拟采用的颗粒最大半径为2 mm,最小粒径为0.1 mm,共生成9 275个颗粒.采用围压为50、100、150 kPa,试件目标孔隙率为0.2,细观摩擦系数为0.25,试件模型见图 1.

|
图 1 试件模型 Figure 1 Specimen model |
用迭代法进行宏-细观参数标定,迭代变量为颗粒法向刚度和刚度比.迭代关系式是利用细观参数对曲线形态的影响,将拐点强度σ0和剪切破坏时的偏应力Δσ1-3作为控制参数,不断拟合出合适的法向刚度和刚度比,使得数值模拟的应力应变曲线越来越接近于室内试验得出的应力应变曲线.迭代终止,是通过计算拐点强度和剪切破坏时偏应力的误差率,在可接受范围内即终止迭代.
已有研究[15]表明,根据各细观参数对宏观参数的影响程度,由强到弱排序,依次为:法向和切向的刚度比、细观摩擦系数、剪切速率、颗粒粒径分布、孔隙度.为了更加接近室内试验,数值模拟试验中剪切速率、颗粒粒径分布和孔隙度均与室内试验保持一致.在数值模拟过程中发现:1) 在接触黏结模型中,对应力应变曲线形态影响较大的是颗粒刚度值的大小和刚度比的大小.由于颗粒之间是点接触,接触面积趋近于0,颗粒间的黏结强度和细观摩擦系数对应力应变曲线影响很小. 2) 在平行黏结模型中,颗粒刚度、刚度比、颗粒间黏结强度均对应力应变曲线形态有较大的影响,而细观摩擦系数对应力应变曲线影响较小.
经多次试验发现,在颗粒刚度、刚度比、黏结强度和细观摩擦系数4个影响参数中,对颗粒刚度和刚度比进行迭代是确定宏-细观参数最有效的方法.每次迭代分3个步骤:1) 确定法向刚度Kn值; 2) 确定刚度比Kn/Ks; 3) 计算误差率,判断是否进行下次迭代.以线性接触模型为例,具体迭代过程如下.
第1步 设置试验1,确定Kn值.试验1中共设置8组试验,选定初始参数:8组试验中法向黏结强度和切向黏结强度均为50 kN·m-1,围压为100 kPa,细观摩擦系数采用0.25,颗粒法向黏结强度和切向黏结强度比值为1,颗粒平均半径Rc=1.05 mm,颗粒法向刚度分别为8.0、9.0、10.0、11.3、12.0、13.0、14.0、15.0 kN·m-1.数值试验模拟得出的应力应变曲线如图 2所示.

|
图 2 不同法向刚度下应力应变曲线 Figure 2 Stress-strain curve under different normal stiffness |
从图 3中可以明显看出,当颗粒的法向刚度与切向刚度不断增大时,应力应变曲线的峰值强度也不断增大.定义应力应变曲线中偏应力不再随着应变线性增长的点为曲线拐点,根据试验结果提取应力应变曲线的拐点强度σ0,提取结果如下.当Kn值为8.0、9.0、10.0、11.3、12.0、13.0、14.0、15.0 kN· m-1时,拐点强度分别为54.84、67.12、78.98、98.11、101.47、112.44、122.53、136.50 kPa.根据结果绘制散点图并进行拟合,如图 3所示,拟合结果为

|
图 3 不同颗粒刚度下拐点强度散点图 Figure 3 The inflection point strength of different particle stiffness |
| $ {{K}_{\rm{n}}}=\rm{0}\rm{.03163+8}\rm{.7348}{{\sigma }_{0}}. $ | (1) |
式中:Kn为法向刚度,kN·m-1; σ0为拐点强度,kPa.室内试验拐点强度为101.3 kPa,将其代入到公式得Kn的值为12.011 35 kN·m-1.
第2步 根据试验1得出的Kn设置试验2,通过试验2确定合适的Kn/Ks(即确定合适的切向刚度Ks).试验参数:围压为100 kPa,细观摩擦系数为0.25,颗粒法向黏结强度和切向黏结强度比值为1,颗粒黏结强度均为50 kN·m-1,其他参数设置以及提取的剪切破坏时偏应力Δσ1-3见表 1.
| 表 1 试验2参数及结果 Table 1 arameters and results of test 2 |
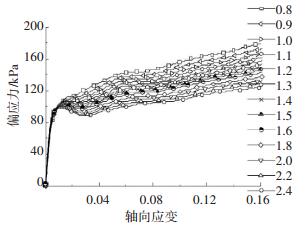
找出与室内试验Δσ1-3相近的那一组数值模拟试验.室内试验的Δσ1-3分别为93.4 kPa (围压为50 kPa时)、124 kPa(围压为100 kPa时)、144.02 kPa(围压为150 kPa时).数值模拟结果应力应变曲线如图 4所示.
|
图 4 不同刚度比下应力应变曲线 Figure 4 Stress-strain curve under different stiffness ratios |
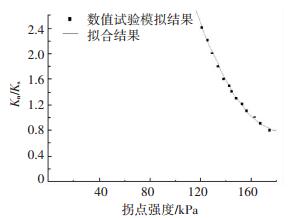
对试验结果进行拟合,得到100 kPa围压下颗粒刚度比与剪切破坏时偏应力的关系, 见图 5.从图 4、5中可以得出,颗粒刚度比不影响应力应变曲线的拐点强度和弹性模量,但随着颗粒刚度比的增大Δσ1-3不断减小.根据试验数据绘制刚度比与Δσ1-3的散点图,如图 5所示,并对其进行拟合,拟合结果为
|
图 5 不同刚度比下剪切破坏时偏应力变化曲线 Figure 5 The variation curve of the shear failure deviator stress at different stiffness ratios |
| $ \begin{align} &{{K}_{\rm{n}}}/{{K}_{\rm{s}}}=14.922\ 56-15.383\ 36\Delta {{\sigma }_{1-3}}+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ 4.186\ 85\Delta {{\sigma }_{1-3}}^{2}. \\ \end{align} $ | (2) |
式中Δσ1-3的单位为105 Pa.室内试验的Δσ1-3为124 kPa,将Δσ1-3=1.24代入到公式中,得到Kn/Ks= 2.28.
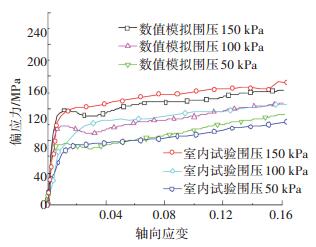
第3步 设置试验3,采用试验1确定的颗粒法向刚度以及试验2确定的颗粒刚度比,分别在围压50、100、150 kPa的情况下对试样进行数值模拟,结果如图 6所示.
|
图 6 应力应变曲线 Figure 6 Stress-strain curve |
提取图中6组应力应变曲线的室内试验拐点强度Δσ0室内、数值模拟试验拐点强度Δσ0数值、室内试验峰值强度Δσ1-3室内和数值模拟试验峰值强度Δσ1-3数值,计算室内试验和数值试验的误差率,结果如表 2中所示.从图中看出,数值试验的应力应变曲线形态与室内试验的相似,从表中可以看出,在围压50 kPa时,Δσ1-3误差率大于5%,其他5组参考数据的误差率都在5%以内,数值模拟效果良好.
| 表 2 试验3结果 Table 2 Results of test 3 |
经过试验1、2、3就完成了一步迭代标定,如果数值试验结果与室内试验结果有较大的出入或是没有达到预定的精度,那么就在第1步迭代的基础上进行第2步迭代,继续标定颗粒的刚度和黏结强度,直至达到所需的精度为止.经过多次试验证明,这种迭代方法,所模拟出来的应力应变曲线最终会接近于室内试验所得到的应力应变曲线.
2 各细观参数对应力应变曲线的影响 2.1 Kn及Kn/ Ks对应力应变曲线的影响图 7中的应力应变曲线是试验1轴向应变0~0.003内的放大图,徐小敏等认为轴向应变在1%内轴向应变增量与轴向应变几乎成线性关系[5],图中的结果与其结论是一致的.从图中可看出刚度比等其他细观参数不变时颗粒法向刚度越大初始杨氏模量越大.

|
图 7 不同法向刚度下应力应变曲线 Figure 7 Stress-strain curve under different normal stiffness |
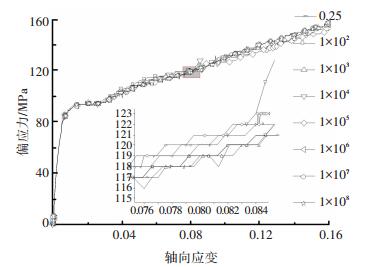
摩擦系数在细观和宏观上存在差异性,宏观摩擦系数取值为0~1,而细观摩擦系数取值理论上为0~+∝. 图 8为在试验3的基础上,只改变细观摩擦系数大小得出的8条应力应变曲线,从局部放大图中可看出细观摩擦系数对应力应变曲线的形态只有细微的影响. 图 9为在试验3的基础上将围压从100 kPa提高到100 MPa所得出的6条应力应变曲线,从图中可以看出,细观摩擦系数对于剪切破坏时的偏应力有很大影响,随着细观摩擦系数的增大,抗剪强度也不断增大.对比两图可知,当围压较小的时候,模型抗剪强度受细观摩擦系数的影响较小,当围压较大时,则不能忽略细观摩擦系数的影响.
|
图 8 不同细观摩擦系数下应力应变曲线(100 kPa) Figure 8 Stress-strain curve under different meso friction coefficients (100 kPa) |

|
图 9 不同细观摩擦系数下应力应变曲线图(100 MPa) Figure 9 Stress-strain curve under different meso friction coefficients (100 MPa) |
基于线性接触的分析发现黏结强度对于应力应变曲线没有明显影响,这是因为接触黏结模型中球是刚性的、且接触面积趋近于0,当受到外力作用时,容易产生滑移,小球之间的咬合作用极小,所以黏结强度对线性接触模型中的抗剪强度没有太大影响.
图 10中是基于平行黏结模型得出的应力应变曲线,切向、法向黏结强度比值为1,其他参数不变,只改变黏结强度的大小.从图中可得出,黏结强度越大偏应力峰值强度越大.平行黏结模型中颗粒接触允许有一定的重叠量,平行黏结接触面积远大于线性模型的接触面积,这样法向黏结强度增大了小球间的抗拉能力,切向黏结强度增大了小球间的切向抗剪能力,总体上提高了小球间的咬合力,从而提高了模型的抗剪能力.

|
图 10 不同黏结强度下应力应变曲线 Figure 10 Stress-strain curve under different bond strengths |
1) 对颗粒法向刚度和刚度比进行迭代是最有效确定宏-细观参数的方法.试验证明,利用初始值不断循环迭代可使数值模拟试验结果更加接近室内三轴试验的结果,迭代标定法可以减少无效的“试参数”工作,提高参数标定工作效率,且误差率可控.
2) 颗粒的法向刚度与切向刚度不断增大时,应力应变曲线的Δσ1-3也不断增大.颗粒法向刚度越大初始杨氏模量越大.颗粒刚度比不影响应力应变曲线的拐点强度和弹性模量,但随着颗粒刚度比的增大, Δσ1-3不断减小.
3) 接触黏结模型中,黏结强度对应力应变曲线的破坏时偏应力几乎没有影响.在平行黏结模型中,随着黏结强度的不断增大,模型的抗剪能力不断增大,剪切破坏时偏应力也不断增大.
4) 围压较小时,细观摩擦系数对应力应变曲线的影响极其微小.围压较大时,随着细观摩擦系数的增大,模型的抗剪强度也随之增大,此时细观摩擦系数的影响不可忽略.围压大小与细观摩擦系数对应力应变曲线影响的内在关系,在以后的研究工作中还需要深入探讨.
| [1] |
周健, 陈小亮, 杨永香, 等. 饱和层状砂土液化特性的动三轴试验研究[J].
岩土力学, 2011, 32(4): 967-972.
ZHOU Jian, CHEN Xiaoliang, YANG Yongxiang, et al. Study of liquefaction characteristics of saturated stratified sands by dynamic triaxial test[J]. Rock and Soil Mechanics, 2011, 32(4): 967-972. |
| [2] |
周健, 王家全, 孔祥利, 等. 砂土颗粒与土工合成材料接触界面细观研究[J].
岩土工程学报, 2010(1): 61-67.
ZHOU Jian, WANG Jiaquan, KONG Xiangli, et al. Mesoscopic study of the interface between sandy soil and geosynthetics[J]. Chinese Journal of Geotechnical Engineering, 2010(1): 61-67. |
| [3] |
周健, 池毓蔚, 池永, 等. 砂土双轴试验的颗粒流模拟[J].
岩土工程学报, 2000, 22(6): 701-704.
ZHOU Jian, CHI Yuwei, CHI Yong, et al. Simulation of biaxial test on sand by particle flow code[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(6): 701-704. |
| [4] |
周健, 池永. 砂土力学性质的细观模拟[J].
岩土力学, 2003, 24(6): 901-906.
ZHOU Jian, CHI Yong. Mesomechanical simulation of sand mechanical properties[J]. Rock and Soil Mechanics, 2003, 24(6): 901-906. |
| [5] |
周健, 姚志雄, 张刚, 等. 砂土渗流过程的细观数值模拟[J].
岩土工程学报, 2007, 29(7): 977-981.
ZHOU Jian, YAO Zhixiong, ZHANG Gang, et al. Mesomechanical simulation of seepage flow in sandy soil[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(7): 977-981. |
| [6] |
周健, 郭建军, 张昭, 等. 砂土中单桩静载室内模型试验及颗粒流数值模拟[J].
岩土力学, 2010, 31(6): 1763-1768.
ZHOU Jian, GUO Jianjun, ZHANG Zhao, et al. Model test of single pile static load in sands and numerical simulation using particle flow code[J]. Rock and Soil Mechanics, 2010, 31(6): 1763-1768. |
| [7] |
李识博, 王常明, 王念秦, 等. 黄土三轴试验的颗粒流数值模拟[J].
中国公路学报, 2013, 26(6): 22-29.
LI Shibo, WANG Changming, WANG Nianqin, et al. Numerical simulation of loess triaxial shear test by PFC3D[J]. China Journal of Highway and Transport, 2013, 26(6): 22-29. |
| [8] |
姜景山, 刘汉龙, 程展林, 等. 密度和围压对粗粒土力学性质的影响[J].
长江科学院院报, 2009, 26(8): 46-50.
JIANG Jingshan, LIU Hanlong, CHENG Zhanlin, et al. Influences of density and confining pressure on mechanical properties for coarse grained soils[J]. Journal of Yangtze River Scientific Research Institute, 2009, 26(8): 46-50. |
| [9] |
徐小敏, 凌道盛, 陈云敏, 等. 基于线性接触模型的颗粒材料细-宏观弹性常数相关关系研究[J].
岩土工程学报, 2010, 32(7): 991-998.
XU Xiaomin, LING Daosheng, CHEN Yunmin, et al. Correlation of microscopic and macroscopic elastic constants of granular materials based on linear contact model[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(7): 991-998. |
| [10] |
邢纪波, 王泳嘉. 离散单元法的计算参数和求解方法选择[J].
计算力学学报, 1999, 16(1): 47-51.
XING Jibo, WANG Yongjia. Determination of calculating parameters and solution methods of discrete element method[J]. Chinese Journal of Computational Mechannics, 1999, 16(1): 47-51. |
| [11] |
张振南, 葛修润, 李永和. 基于虚内键理论的材料多尺度力学模型[J].
固体力学学报, 2006, 27(4): 325-329.
ZHANG Zhennan, GE Xiurun, LI Yonghe. A multiscale mechanical model of materials based on virtual internal bond theory[J]. Acta Mechanica Solid Sinica, 2006, 27(4): 325-329. |
| [12] |
蒋明镜, 付昌, 刘静德, 等. 不同沉积方向各向异性结构性砂土离散元力学特性分析[J].
岩土工程学报, 2016, 38(1): 138-146.
JIANG Mingjing, FU Chang, LIU Jingde, et al. DEM simulations of anisotropic structured sand with different deposit directions[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(1): 138-146. DOI: 10.11779/CJGE201601015 |
| [13] |
周博, 黄润秋, 汪华斌, 等. 基于离散元法的砂土破碎演化规律研究[J].
岩土力学, 2014(9): 2709-2716.
ZHOU Bo, HUANG Runqiu, WANG Huabin, et al. Study of evolution of sand crushability based on discrete elements method[J]. Rock and Soil Mechanics, 2014(9): 2709-2716. |
| [14] |
李宁, 高岳. 透明砂土三轴试验的颗粒流模拟[C]//全国工程地质学术年会. 北京: 工程地质学报, 2011.
LI Ning, GAO Yue. PFC simulation on triaxial shear test of transparent sand[C]//Annual meeting of national engineering geology. Beijing: Journal of Engineering Geology, 2011. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-GCDZ201108001058.htm |
| [15] |
张志华. 基于PFC3D的粗粒土三轴试验细观数值模拟[D]. 宜昌: 三峡大学, 2015.
ZHANG Zhihua. Mesoscopic numerical simulation of triaxial test of coarse grained soil based on PFC3D[D]. Yichang:Three Gorges University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-11075-1015042838.htm |
 2017, Vol. 49
2017, Vol. 49


