2. 现代城市交通技术江苏高校协同创新中心, 南京 210096;
3. 桂林电子科技大学 建筑与交通工程学院, 广西 桂林 541004;
4. 华蓝设计(集团)有限公司, 南宁 530011
2. Jiangsu Province Collaborative Innovation Center of Modern Urban Traffic Technologies, Nanjing 210096, China;
3. School of Architecture and Transportation Engineering, Guilin University of Electronic Technology, Guilin 541004, Guangxi, China;
4. Hualan Design and Consulting Group, Nanning 530011, China
自动驾驶汽车与车联网技术的发展,使得未来交通流由人工驾驶车辆、协同自适应巡航控制(cooperative adaptive cruise control, CACC)车辆随机混合而成.由于人工驾驶车辆缺乏车车通信设备,紧跟人工车辆的CACC车辆因无法接收到前方车辆的信息而自动退化为自适应巡航控制(adaptive cruise control, ACC)车辆[1].
针对这种混合交通流特性的研究,国外研究开展较早,成果主要集中在通行能力[2]、交通安全[3]、交通污染[4]等方面.但针对驾驶舒适性的研究开展较少[5],且缺乏对舒适性研究结果内在原因的分析.此外,很多研究中应用的ACC模型与CACC模型缺乏与实车实验的对比.相比而言,国内研究起步较晚,虽然涉及ACC与CACC控制技术的设计[6],但国内鲜有文献对这种混合交通环境下的驾驶舒适性开展研究.
鉴于此,应用加州伯克利PATH实验室实车验证的ACC模型和CACC模型,研究不同CACC市场率时的驾驶舒适性.考虑到舒适性本质上体现了车辆偏离平衡态时的加减速过程,从混合交通流稳定性的角度阐述舒适性仿真结果的内在原因.
为了不引起混淆,本文CACC市场率是指CACC车辆没有退化为ACC车辆之前所占的交通流总车辆数的比例. CACC市场率记为p,人工驾驶车辆比例为1-p,ACC车辆比例由退化前的CACC车辆与人工驾驶车辆相对位置随机产生.
1 跟驰模型 1.1 人工驾驶车辆IDM(intelligent driver model)跟驰模型[7]被广泛应用于人工车辆的仿真研究,其模型为
| $ \dot {v} = a\left[{1-{{\left( {\frac{v}{{{v_0}}}} \right)}^4}-{{\left( {\frac{{{s_0} + vT + \frac{{v\Delta v}}{{2\sqrt {ab} }}}}{s}} \right)}^2}} \right]. $ | (1) |
式中:a为最大加速度,v0为自由流速度,s0为最小停车间距,T为安全车头时距,b为舒适减速度,Δv为相邻车辆的速度差项.依据文献[8-9],a取值为1.0 m/s2,v0取值为33.3 m/s,s0取值为2.0 m,T取值为1.5 s,b取值为2.0 m/s2.
1.2 ACC车辆应用文献[9]通过实车实验标定的ACC模型,该模型可较好反应目前商用ACC控制系统应用于真实车辆的跟驰特性.由于该ACC控制系统并不具有驾驶员驾驶行为差异性,因此可应用于我国交通流特性的研究.模型为
| $ \dot {v} ={k_1}\left( {h-l-{s_0}-{T_A}v} \right) + {k_2}\Delta v. $ | (2) |
式中:h为车头间距,l为车长,s0为最小停车间距,TA为ACC期望车间时距,k1和k2为控制系数,依据文献[9],k1取值为0.23,k2取值为0.07.依据文献[10],TA取值为1.1、1.6、2.2 s时的接受比率分别为50.4%、18.5%、31.1%.
1.3 CACC车辆PATH依据CACC上层控制器设计[11],提出了基于速度控制的CACC模型,并通过实车实验验证了该CACC模型能够用于真实CACC车辆的仿真研究[9].由于CACC车辆跟驰特性并不取决于驾驶员差异性,因此该CACC模型同样可适用于我国交通流特性研究.模型为
| $ \left\{ \begin{array}{l} v = {v_{\rm{p}}} + {k_{\rm{p}}}e + {k_{\rm{d}}}\dot {e}, \\ e = h-{s_0}-l-{T_{\rm{C}}}v. \end{array} \right. $ | (3) |
式中:vp为前一控制时刻的速度,e为实际车间距与期望车间距的误差,h、l、s0含义同式(2),TC为CACC期望车间时距,kp、kd为控制系数.实车实验对kp和kd的标定结果为:kp=0.45,kd=0.25.依据文献[10],TC取值为0.6、0.7、0.9、1.1 s时的接受比率分别为57.0%、24.0%、7.0%、12.0%.
2 评价指标应用基于国际ISO 2631-1标准的驾驶舒适性指标[12],评价不同CACC市场率时的舒适性.文献[12]对国际ISO 2631-1舒适性指标进行了较详细阐述,舒适性指标为
| $ C = {\left[{\frac{1}{m}\sum\limits_{i = 0}^m {a_i^2} } \right]^{\frac{1}{2}}}. $ | (4) |
式中:ai为统计获取的第i个加速度值,m为加速度统计总量.文献[12]将舒适性分为6个等级,如表 1所示.
| 表 1 舒适性等级 Table 1 Comfort index level |
舒适性指标反应的是车辆加速度情况,而匝道合流区是扰动常发区域,加速度变化较为频繁,因此针对含有匝道的高速公路交通场景,基于数值仿真实验评估舒适性具有较好代表性,数值仿真实验基于MATLAB仿真软件.
3.1 实验结果TA、TC的最大接受比例取值分别为1.1、0.6 s[10],以TA=1.1 s,TC=0.6 s为例,基于数值仿真实验研究混合交通流舒适性.并在3.2节对TA和TC进行参数敏感性分析.
数值仿真实验路段如图 1所示,路段长度为6 km,匝道位于3 km位置处,匝道区为500 m,由于本文关注匝道汇入行为对主路车流造成的影响,依据文献[13]中的模拟机制,仿真中对主路车流在匝道区进行随机减速,且减速范围参照文献[14].在匝道区及其上下游800 m内布设虚拟检测器,检测器间隔为50 m.在仿真实验中,CACC市场率p随机地确定驶入车辆为CACC车辆或者人工驾驶车辆.若该驶入车辆为CACC车辆,在其紧跟人工车辆时,需退化为ACC车辆.考虑仿真实验中3种车型相对数量、位置的随机性,各CACC市场率下均独立进行3次仿真,并取均值作为该CACC市场率下的舒适性仿真结果,当CACC市场率p等于0、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0时,C指标均值分别为0.499、0.502、0.514、0.517、0.525、0.537、0.677、0.705、0.637、0.414、0.277.因此,随着CACC市场率p的增加,舒适性C指标呈现出先变大再减小的变化趋势,表明舒适性逐渐变差,然后再逐步恢复并得到提高.对照表 1中C取值范围与舒适性等级之间的关系,将C值仿真结果转换为舒适性等级的变化趋势,如图 2所示.由图 2可知,随着p的增加,舒适性由等级4逐步恶化至等级3,尔后再恢复并提升至等级5,当p大于80%时,舒适性的提升较为显著.

|
图 1 仿真路段示意图 Figure 1 Road section in simulations |

|
图 2 舒适性等级结果(TA= 1.1 s,TC =0.6 s) Figure 2 Results of comfort level (TA=1.1 s, TC=0.6 s) |
在对TC进行参数敏感性分析时,TA取接受比率最大时的1.1 s.考虑到随机性影响,每次仿真实验均进行3次,结果如表 2所示.为了直观地看出TC取值对舒适性的影响,计算得到舒适性C指标值随CACC市场率p变化的趋势,如图 3所示.同时,按照表 1中C指标值对应的舒适性等级,得到不同TC、p取值时的舒适性等级热力图,如图 4所示.在图 4中,各TC与p对应的小方格颜色值为舒适性等级数值,且该颜色值能够反映两个舒适性等级之间的情况.
| 表 2 TC参数敏感性分析结果(TA= 1.1 s) Table 2 Results of sensitivity analysis on TC (TA=1.1 s) |

|
图 3 TC敏感性分析的C指标值(TA= 1.1 s) Figure 3 C of sensitivity analysis on TC (TA=1.1 s) |

|
图 4 TC敏感性分析的舒适性等级(TA= 1.1 s) Figure 4 Comfort level of sensitivity analysis on TC (TA=1.1 s) |
由图 3可知,随着p增加,C指标值先变大再减小的变化趋势与TC取值无关.且同一p值下,不同TC取值时的C指标值基本相当.表明了舒适性指标C值的大小不依赖于TC取值的大小.由图 4可知,随着p的增加,舒适性等级变化趋势与TC取值无关,均由等级4恶化至等级3,然后再恢复并提升至等级5,且在p大于80%时,舒适性的提升较为明显,这与图 2中的结果相一致.
3.2.2 TA参数敏感性分析在对TA取值进行参数敏感性分析,TC取接受比率最大时的0.6 s. TA参数敏感性分析结果如表 3所示,同时计算得到C随p增加的变化趋势,如图 5所示.同时依据表 1中C值对应的舒适性等级,得到不同TA、p取值时的舒适性等级热力图,如图 6所示.
| 表 3 TA参数敏感性分析结果(TC= 0.6 s) Table 3 Results of sensitivity analysis on TA (TC=0.6 s) |

|
图 5 TA敏感性分析的C指标值(TC= 0.6 s) Figure 5 C of sensitivity analysis on TA (TC=0.6 s) |
|
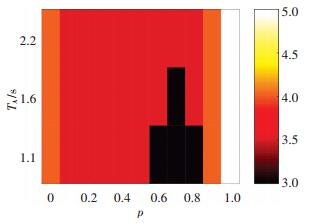
图 6 TA敏感性分析的舒适性等级(TC= 0.6 s) Figure 6 Comfort level of sensitivity analysis on TA (TC=0.6 s) |
由图 5、6可知,不同TA取值时,C指标值随着p的增加,均呈现出先增大后减小的变化过程,同时舒适性等级呈现出先降低后增加的变化趋势.表明在p逐步普及的过程中,舒适性会逐步恶化,然后恢复并得到提升,这与3.1节中的仿真结果相一致.此外,在同一p取值下,TA取值增大时,C指标值明显减小,且舒适性等级明显增加.表明在p逐渐增加时,TA取值越大,越有利于抑制舒适性的恶化程度,但舒适性在p达到80%以后,才能够得到显著提升.
4 讨论舒适性本质上体现了交通流由平衡态变为非平衡态时的动态加减速过程,因此,针对第3节舒适性随CACC市场率增加的变化趋势,以及TA、TC取值对舒适性的影响,从混合交通流稳定性的角度阐述其内在原因.
4.1 跟驰模型稳定性分析3种车型跟驰模型的稳定性,为4.2节讨论混合交通流在不同CACC市场率下的稳定性作铺垫.文献[15]推导了跟驰模型一般稳定性条件为
| $ \frac{1}{2}{\left( {{f^v}} \right)^2}-{f^{\Delta v}}{f^v}-{f^h} < 0. $ | (5) |
式中:fv、fΔv、fh分别为跟驰模型公式对速度、速度差和车头间距在平衡态时的偏微分.因此,可计算人工车辆、ACC车辆、CACC车辆各自稳定时应满足的条件分别如式(6)、(7)、(8) 所示.其中Δt为依据文献[16]进行推导时,由一阶泰勒展开产生的时间步长,取值0.01 s.式(6)~(8) 中其余参数均为对应的跟驰模型参数.
| $ \left\{ \begin{array}{l} \frac{1}{2}{\left( {f_{\rm{R}}^v} \right)^2}- f_{\rm{R}}^{\Delta v}f_{\rm{R}}^v- f_{\rm{R}}^h < 0, \\ f_{\rm{R}}^v = \frac{{4a{v^3}}}{{{v_0}^4}}- \frac{{2aT\left[{1-{{\left( {v/{v_0}} \right)}^4}} \right]}}{{{s_0} + vT}}, \\ f_{\rm{R}}^{\Delta v} = \sqrt {\frac{a}{b}} \frac{{\left[{1-{{\left( {v/{v_0}} \right)}^4}} \right]}}{{{s_0} + vT}}, \\ f_{\rm{R}}^h = 2a\frac{{\left[{1-{{\left( {v/{v_0}} \right)}^4}} \right]\sqrt {1 -{{\left( {v/{v_0}} \right)}^4}} }}{{{s_0} + vT}}. \end{array} \right. $ | (6) |
| $ \left\{ \begin{array}{l} \frac{1}{2}{\left( {f_{\rm{A}}^v} \right)^2}-f_{\rm{A}}^{\Delta v}f_{\rm{A}}^v-f_{\rm{A}}^h < 0, \\ f_{\rm{A}}^v = -{k_1}{T_{\rm{A}}}, \\ f_{\rm{A}}^{\Delta v} = {k_2}, \\ f_{\rm{C}}^h = {k_1}. \end{array} \right. $ | (7) |
| $ \left\{ \begin{array}{l} \frac{1}{2}{\left( {f_{\rm{C}}^v} \right)^2}-f_{\rm{C}}^{\Delta v}f_{\rm{C}}^v-f_{\rm{C}}^h < 0, \\ f_{\rm{C}}^v =-\frac{{{k_p}{T_{\rm{C}}}}}{{\Delta t + {k_{\rm{d}}}{T_{\rm{C}}}}}, \\ f_{\rm{C}}^{\Delta v} = \frac{{{k_d}}}{{\Delta t + {k_{\rm{d}}}{T_{\rm{C}}}}}, \\ f_{\rm{C}}^h = \frac{{{k_p}}}{{\Delta t + {k_{\rm{d}}}{T_{\rm{C}}}}}. \end{array} \right. $ | (8) |
依据式(6)~(8) 计算可知,人工驾驶车辆在0~0.6 m·s-1和21.4~33.3 m·s-1的速度时稳定,在0.6~21.4 m·s-1时不稳定. ACC车辆在自由流速度内均不稳定,CACC车辆在自由流速度内均稳定.
4.2 舒适性变化趋势原因分析在舒适性仿真实验中,车辆的加减速过程包含了人工驾驶车辆的不稳定速度范围,依据PATH实车实验[9],目前控制水平下的ACC车辆较人工驾驶车辆更加不稳定,在CACC市场率较小的阶段,由于车辆位置分布的随机性,造成CACC车辆分散在人工驾驶车辆之间,大部分退化为ACC车辆,使得混合交通流稳定性出现恶化.随着CACC市场率增大到较高阶段,CACC车辆退化为ACC车辆的概率减小,CACC车辆较好的稳定性使得混合交通流不稳定情况得到改善,并最终达到稳定状态.以TA=1.1 s,TC=0.6 s为例,混合交通流稳定性仿真结果如图 7所示.在图 7中,车队包含60辆车,3种车型相对数量、位置均由CACC市场率p随机产生,且紧跟人工驾驶车辆的CACC车辆退化为ACC车辆,车队以17 m/s的平衡态速度行驶,头车产生1 m/s2的减速度扰动打破车队平衡态,头车扰动持续3 s.

|
图 7 混合交通流稳定性 Figure 7 String stability of mixed traffic flow |
由图 7可以看出,混合交通流稳定性随着p的增加,呈现出先恶化、再逐步改善并达到稳定的变化趋势,表明混合交通流稳定性的变化趋势与舒适性的变化趋势一致.如前所述,舒适性本质上体现了交通流背离平衡态的加减速过程.因此,在p逐步增加的过程中,混合交通流稳定性的变化趋势定性地影响了舒适性变化趋势.并且,在p超过80%以后,车队最终变为稳定状态,使得舒适性得到明显提升.此外,由于ACC车辆不稳定性与TA取值无关,且TC取不同值时,CACC车辆均稳定,使得混合交通流稳定性变化趋势与TA和TC取值无关,这是第3节仿真中TA和TC取值并不影响舒适性变化趋势的原因.
4.3 TA、TC对舒适程度影响的原因分析由第3节可知,TA取值较大时,有利于抑制舒适性的恶化程度,而TC取值不同并不影响舒适性的舒适程度.通过分析TA、TC取不同值时,ACC车辆和CACC车辆减速时的速度、加速度动态特性,进行原因阐述.
假设在图 7的仿真实验中,车队头车(前车)的紧跟车辆(后车)分别为人工驾驶车辆、ACC车辆和CACC车辆时,后车在前车扰动下的速度与加速度动态变化分别如图 8、9所示.

|
图 8 速度动态变化 Figure 8 Dynamic change of velocity |
|
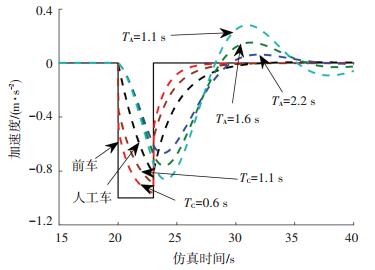
图 9 加速度动态变化 Figure 9 Dynamic change of acceleration |
由图 8、9可知,TA取值不同时,ACC车辆速度、加速度动态特性均比人工驾驶车辆差,这与PATH的实车实验相符合[9],这也是4.2节仿真中混合交通流稳定性存在恶化趋势的原因. TA取值越大,ACC车辆的速度和加速度动态特性有所改善,因此有利于抑制混合交通流稳定性的恶化,这是TA取值越大,越有利于抑制舒适性恶化程度的原因.而TC取值不同时,CACC车辆速度和加速度动态特性均稳定,使得舒适性不受TC取值的影响.
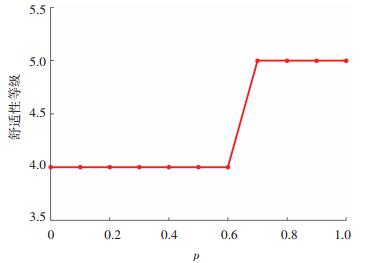
4.4 车车通信环境下的舒适性由上面分析可知,ACC车辆的不稳定性使得在p逐步普及的过程中,舒适性存在先恶化、再逐步恢复并得到提升的趋势.若人工车辆均安装车车通信设备,则混合交通流由人工驾驶车辆和CACC车辆两种车型构成.以TC=0.6 s为例,假设人工驾驶车辆均安装车车通信设备,获得舒适性等级随p变化的曲线如图 10所示.对比图 10与第3节的仿真结果可知,车车通信环境下舒适性随p的增加而逐步得到提升.
|
图 10 车车通信时的舒适性 Figure 10 Comfort of vehicle-to-vehicle communications |
1) 随着CACC市场率的增加,人工车辆、ACC车辆和CACC车辆的混合交通流稳定性先恶化、然后逐步恢复至稳定状态.稳定性变化趋势定性地决定了舒适性变化趋势,使得混合交通流舒适性呈现出先恶化、再恢复、最后得到提升的变化趋势.
2) 车辆加减速时的速度与加速度动态特性决定了舒适性变化趋势不受ACC、CACC期望车间时距取值的影响. ACC期望车间时距越大,越有利于抑制舒适性的恶化程度. CACC车辆有利于舒适性的提升,但舒适性程度并不受CACC期望车间时距取值的影响.人工车辆安装车车通信设备时,由人工车辆和CACC车辆构成的混合交通流舒适性随着CACC车辆的普及呈现出逐步改善的趋势.
3) 目前尚不具备大规模真车实验条件,只能针对不同CACC市场率舒适性的仿真研究作为真车实验实施前的前期探索,为未来大规模真车实验的实施提供参考.同时,驾驶舒适性评价的最佳途径仍然是真实环境下的真车实验,因此本文舒适性的仿真研究具有模型指标化替代手段的一般局限性.
| [1] |
PLOEG J, SEMSAR-KAZEROONI E, LIJSTER G, et al. Graceful degradation of cooperative adaptive cruise control[J].
IEEE Transactions on Intelligent Transportation Systems, 2015, 16(1): 488-497.
DOI: 10.1109/TITS.2014.2349498 |
| [2] |
VAN AREM B, VAN DRIEL C J G, VISSER R. The impact of cooperative adaptive cruise control on traffic-flow characteristics[J].
IEEE Transactions on Intelligent Transportation Systems, 2006, 7(4): 429-436.
DOI: 10.1109/TITS.2006.884615 |
| [3] |
DEY K C, YAN L, WANG X, et al. A review of communication, driver characteristics, and controls aspects of cooperative adaptive cruise control (CACC)[J].
IEEE Transactions on Intelligent Transportation Systems, 2016, 17(2): 491-509.
DOI: 10.1109/TITS.2015.2483063 |
| [4] |
FAGNANT D J, KOCKELMAN K. Preparing a nation for autonomous vehicles: opportunities, barriers and policy recommendations[J].
Transportation Research Part A: Policy and Practice, 2015, 77: 167-181.
DOI: 10.1016/j.tra.2015.04.003 |
| [5] |
SHLADOVER S E, NOWAKOWSKI C, LU X Y, et al. Cooperative adaptive cruise control: definitions and operating concepts[J].
Transportation Research Record: Journal of the Transportation Research Board, 2015(2489): 145-152.
|
| [6] |
吴光强, 郭晓晓, 张亮修. 汽车自适应巡航跟车多目标鲁棒控制算法设计[J].
哈尔滨工业大学学报, 2016, 48(1): 80-86.
WU Guangqiang, GUO Xiaoxiao, ZHANG Liangxiu. Multiobjective robust adaptive cruise control algorithm design of car following model[J]. Journal of Harbin Institute of Technology, 2016, 48(1): 80-86. DOI: 10.11918/j.issn.0367-6234.2016.01.012. |
| [7] |
TREIBER M, HENNECKE A, HELBING D. Congested traffic states in empirical observations and microscopic simulations[J].
Physical review E, 2000, 62(2): 1805-1824.
DOI: 10.1103/PhysRevE.62.1805 |
| [8] |
KESTING A, TREIBER M, SCHONHOF M, et al. Adaptive cruise control design for active congestion avoidance[J].
Transportation Research Part C: Emerging Technologies, 2008, 16(6): 668-683.
DOI: 10.1016/j.trc.2007.12.004 |
| [9] |
MILANES V, SHLADOVER S E. Modeling cooperative and autonomous adaptive cruise control dynamic responses using experimental data[J].
Transportation Research Part C: Emerging Technologies, 2014, 48: 285-300.
DOI: 10.1016/j.trc.2014.09.001 |
| [10] |
SHLADOVER S, SU D, LU X Y. Impacts of cooperative adaptive cruise control on freeway traffic flow[J].
Transportation Research Record: Journal of the Transportation Research Board, 2012(2324): 63-70.
|
| [11] |
MILANES V, SHLADOVER S E, SPRING J, et al. Cooperative adaptive cruise control in real traffic situations[J].
IEEE Transactions on Intelligent Transportation Systems, 2014, 15(1): 296-305.
DOI: 10.1109/TITS.2013.2278494 |
| [12] |
PADDAN G S, GRIFFIN M J. Evaluation of wholebody vibration in vehicles[J].
Journal of Sound and Vibration, 2002, 253(1): 195-213.
DOI: 10.1006/jsvi.2001.4256 |
| [13] |
LI Y, WANG H, WANG W, et al. Evaluation of the impacts of cooperative adaptive cruise control on reducing rearend collision risks on freeways[J].
Accident Analysis and Prevention, 2017, 98: 87-95.
DOI: 10.1016/j.aap.2016.09.015 |
| [14] |
OH S, YEO H. Estimation of capacity drop in highway merging sections[J].
Transportation Research Record: Journal of the Transportation Research Board, 2012(2286): 111-121.
|
| [15] |
WILSON R E. Mechanisms for spatiotemporal pattern formation in highway traffic models[J].
Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 2008, 366(1872): 2017-2032.
DOI: 10.1098/rsta.2008.0018 |
 2017, Vol. 49
2017, Vol. 49


