2. 城市水资源与水环境国家重点实验室(哈尔滨工业大学),哈尔滨 150090
2. State Key Laboratory of Urban Water Resources and Environment (Harbin Institute of Technology), Harbin 150090, China
A2/O工艺是目前污水处理厂处理城市污水的主流工艺[1],主要分为厌氧段、缺氧段、好氧段[2].由于该工艺将多种功能菌群置于同一系统中,且系统在厌氧、缺氧、好氧状态下交替运行,不可避免地会引起系统内的菌群基质竞争以及其他一些固有矛盾.功能菌群对水体中营养物质、生存空间的竞争及由生存环境引起的矛盾等构成了A2/O工艺固有的不足.实际上,影响A2/O工艺系统性能的因素有许多,如污泥龄(SRT)、各区段溶解氧(DO)质量浓度、混合液回流比(R)、污泥回流比(r)、水力停留时间(HRT)、水体温度(T)、pH等.这些参数对A2/O工艺的运行会产生复杂的综合影响,对这些参数进行优化,对于提高A2/O工艺的运行效率十分有意义.近年来,国内外学者对A2/O工艺参数的优化进行了探究.Wang等[3]考察了长污泥停留时间对A2/O工艺生物除磷的影响.Zhang等[4]研究了优化体积比对A2/O-BCO(生物接触氧化)工艺脱氮除磷的影响.Chen等[5]则对硝酸盐回流比对A2/O-BAF联用工艺处理效果的影响进行了研究.吴昌永[6]分别考察了SRT、R、r、DO等多个参数对A2/O工艺性能的影响.李永峰等[7]探究了HRT对A2/O工艺系统脱氮除磷效率的影响.刘云雪等[8]考察了r对A2/O工艺运行结果的影响.王建龙等[9]通过试验考察了R对A2/O工艺效能的影响.陈昆柏等[10]则根据FCASM2-HYDRO模型分别建立了厌氧池、缺氧池、好氧池的数值模拟方程,利用有限元法并由数学软件matlab编程求解,得到试验的最佳运行工况.马建立等[11]通过正交试验得到了倒置A2/O工艺处理城镇生活污水的最佳试验条件.
事实上,影响A2/O工艺运行效果的各个因素之间相互联系、相互作用[12-14].仅仅通过控制单一变量法无法将运行参数对A2/O工艺系统的综合影响效果全面反映出来.部分学者考虑到该问题,设计了正交试验来考察多个运行参数对工艺的影响.与控制单一变量法相比,更接近于系统复杂的实际情况.但是正交试验也有其自身的不足.为了方便分析、减少工作量,正交试验中对象因素和因素水平的个数不能太多.同时,正交设计试验选取的是典型点,并未考察其他“非典型点”的情况.无疑,对于有众多影响因素的A2/O工艺,正交试验仍然不能完全满足要求.为进一步得到相对更优的A2/O工艺运行参数组合,在结合前人工作的基础上,提出一种优化A2/O工艺运行参数的新思路:建立基于遗传算法的神经网络模型(GA-ANN模型),对A2/O工艺运行参数进行优化,得到最佳运行参数组合,提高工艺运行效率.
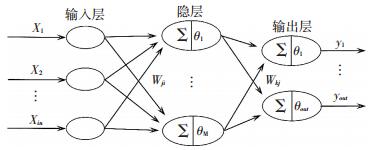
1 GA-ANN模型 1.1 神经网络模型神经网络模型属于黑箱模型(经验模型),具有良好的非线性逼近能力,可以实现多维空间到多维空间上的复杂映射关系,因此,可根据训练好的神经网络对出水指标等进行预测.目前,已有许多学者将神经网络模型应用在污水处理建模上.如张群英[15]利用神经网络建立了污水指标软测量模型,仿真实验证明模型具有较高的适用性与实用性.胡康等[16]利用神经网络模型对A2/O工艺出水氨氮进行预测,发现预测值与真实监测值之间的相对误差在6.5%内.可见神经网络模型应用在模拟A2/O工艺运行脱氮除磷过程上能够满足要求,且精度较高.其中,BP神经网络结构如图 1.
|
图 1 BP神经网络模型的结构 Figure 1 Structure of the neural network model |
图 1中in表示输入层数; out表示输出层结点的个数.Xin表示输入层第i(i=1,2,…,in)个输入样本; Yout表示输出层第k(k=1,2,…,out)个输出值; Wji表示连接输入层结点i和隐含层结点j(j=1,2,…,M)的权值; Wkj表示连接隐含层结点j和输出层结点k的权值.输入与输出之间具有如下关系:
| $ y = f\left( {\sum\limits_{i = 1}^m {{w_i}{x_i}-\theta } } \right). $ | (1) |
式中:θ为阈值,f(X)为激发函数; 可以是线性函数,也可以是非线性函数.常用作用函数有阀值型(硬限制型)、线性型、S型函数(Sigmoid)等.
1.2 遗传算法遗传算法能够较好地处理非连续、非线性、多目标等问题,具有较好的全局寻优能力.应用遗传算法解决相关问题,通常需要完成以下4个方面:
1) 确定基本运行参数.种群大小N、进化代数T、交叉概率、变异概率.
2) 染色体编码与解码.如使用一定长度的二进制符号串随机表示群体中的个体.解码时将二进制符号串转换成为相应的十进制代码.
3) 个体适应度评价.建立合适的适应度函数,保留理想的个体.
4) 遗传算子.包括3种遗传算子,选择运算、交叉运算和变异运算.利用这3种运算,产生新的个体.
根据上述主要步骤以及遗传算法的主要流程,可以方便地利用数学软件Matlab编程来实现遗传算法.刘载文等[17]提出了利用遗传算法对污水处理的优化控制方法,其数值仿真结果证明,在污水处理过程中采用遗传算法寻优是可行和有效的.
2 GA-ANN模型优化A2/O工艺运行参数 2.1 应用方法以污泥回流比r、混合液回流比R、溶解氧质量浓度、温度T、pH等A2/O工艺运行参数作为神经网络模型的输入变量,以出水中的COD、氮、磷等去除率作为输出变量.为了更好地对参数组合进行适应度评价,达到相应要求,需要建立合适的适应度函数(即目标函数).例如,可以构造如下的一个适应度函数:
| $ f = \sum\limits_{i = 1}^n {{\omega _i}{B_i}.} $ | (2) |
式中:f表示适应度,n表示选取的水质指标(如TN、TP、COD等)个数,Bi表示第i个水质指标的去除率,ωi表示i个水质指标去除率的权重.
适应度函数的建立是模型的关键点之一,应根据实际工程要求,全面考虑工艺影响参数而构造.建立适应度函数时,可以综合考虑氮、磷等的去除率,同时为了更加接近实际情况,防止某项指标的去除结果没达到排放标准但适应度值是最优的情况发生,最好能将是否达到排放标准考虑进去,使之在构造的适应度函数中得以体现.这时,可以构造如下的一个适应度函数:
| $ f = \sum\limits_{i = 1}^n {|{C_{0i}}-{C_i}|/{\varphi _i}.} $ | (3) |
式中:f表示适应度,n表示选取的水质指标(如TN、TP、COD等)个数,Ci表示第i个出水指标值,C0i表示第i个出水指标对应的排放标准值,φi表示i个水质指标值降低一个标准单位所产生的经济成本指标权重.
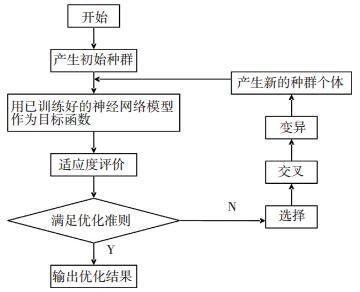
利用神经网络遗传算法极值寻优模型优化A2/O工艺的运行参数,主要包括神经网络训练拟合和遗传算法极值寻优两个部分.神经网络训练拟合首先要构建合适的BP神经网络,用工艺调试的输入(即工艺运行参数)、输出(即研究的出水指标)数据训练BP神经网络,训练后的BP神经网络可以预测输出.遗传算法极值寻优则把训练后的BP神经网络预测输出作为个体适应度值,通过选择、交叉、变异操作寻找工艺的全局最佳输入和最佳输出.基于遗传算法全局寻优的神经网络模型流程见图 2.
|
图 2 基于遗传算法全局寻优的神经网络模型 Figure 2 Neural network model based on the global optimization of genetic algorithm |
整体来说,模型就是首先利用遗传算法生成个体样本,每个样本含有污泥回流比r、混合液回流比R、溶解氧质量浓度DO、温度T、pH等A2/O工艺的运行参数试验值信息,进行优化时输入该样本个体,利用样本数据训练神经网络模型,然后利用该神经网络模型计算目标函数值,再提供给遗传算法做判断:“优胜劣汰”,适应度大的保留.这样嵌套调用,就可以实现A2/O工艺运行参数的优化,获得最优运行参数组合.
2.2 应用实例以某城市A2/O工艺污水处理厂调试为例,借以GA-ANN模型优化工艺运行参数,使得在达到排放标准的基础上,最大限度降低研究的出水指标值.
调试运行期间,工艺参数控制范围如下:进水流量为3 000~6 000 m3/h、污泥回流流量为1 000~ 3 000 m3/h、厌氧池污泥质量浓度为2 500~5 000 mg/L、AO池缺氧段溶解氧质量浓度为0.15~0.5 mg/L、AO池好氧段溶解氧质量浓度为1.000~6.000 mg/L、AO池污泥质量浓度为2 000~5 000 mg/L.该污水处理厂调试运行期间,出水水质基本能达到污水综合排放标准.但是,出水达标并不是处理厂的最终目标,而是在达到排放要求的基础上合理控制成本,使得出水指标值尽可能地降低,提高污水处理厂运行效益.
根据该厂要求,主要对去除化学需氧量进行优化,在获得该污水处理厂调试运行期间在线监测数据后,尝试建立GA-ANN模型,以期得到COD去除效果最好时的参数组合.
输入参数包括:进水流量(X1)、污泥回流流量(X2)、厌氧池污泥质量浓度(X3)、AO池缺氧段溶解氧质量浓度(X4)、AO池好氧段溶解氧质量浓度(X5)、AO池污泥质量浓度(X6)等.最终输出为出水COD(Y).有效数据共有154组,随机取其中2/3的数据用于训练神经网络模型,剩下1/3的数据用于检验建立的神经网络模型.
GA-ANN模型利用数学软件Matlab编程求解.神经网络模型中,基本参数设置如下:迭代次数为100,学习速率为0.05,目标误差为0.000 01.遗传算法模型中,基本运行参数设定如下:种群大小N=50、进化代数T=100、交叉概率Pc=0.7、变异概率Pm=0.1.
程序运行结果如下:
| $ \left. \begin{array}{l} {X_1} = 4\;638.6\\ {X_2} = 2\;559.8\\ {X_3} = 4\;618.4\\ {X_4} = 0.400\;0\\ {X_5} = 4.000\;0\\ {X_6} = 4\;897.7 \end{array} \right\} \Rightarrow {Y_{min}} = 6.200\;0. $ | (4) |
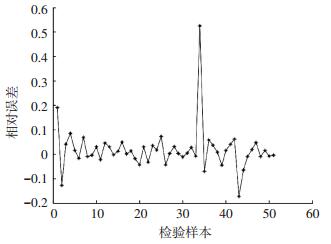
图 3为检验样本的预测输出与期望输出(实际值)的比较,图 4为检验样本的输出预测误差百分比.图 5为遗传算法模型的适应度曲线.即当进水流量为4 638.6 m3/h、污泥回流流量为2 559.8 m3/h、厌氧池污泥质量浓度为4 618.4 mg/L、AO池缺氧段溶解氧质量浓度为0.400 0 mg/L、AO池好氧段溶解氧质量浓度为4.000 0 mg/L、AO池污泥质量浓度为4 897.7 mg/L时,可使出水COD质量浓度最大降低到6.200 mg/L.分析可知,检验样本的输出预测相对误差基本小于10%,且适应度曲线收敛,说明建立基于遗传算法的神经网络模型是可行的.

|
图 3 检验样本的预测输出与期望输出比较 Figure 3 Comparison of the prediction output and the expected output of the test sample |
|
图 4 检验样本的输出预测相对误差 Figure 4 Output prediction relative error of test samples |

|
图 5 适应度曲线 Figure 5 Fitness curve |
对于A2/O工艺这样一个复杂系统,影响工艺处理效率的运行参数众多.因此,设置合适的运行参数,才能使系统运行处于较为理想的状态.根据多年的运行经验,A2/O工艺运行参数设计的大致范围为:污泥回流比20%~100%,好氧池溶解氧质量浓度1~5 mg/L,缺氧池溶解氧质量浓度应≤0.5 mg/L,污泥质量浓度2 000~5 000 mg/L.但是在工程实践中,工艺调试往往将花费大量时间同时不一定能达到调试目的.此时,倘若利用调试的前期数据,运用GA-ANN模型对A2/O工艺运行参数进行优化,不仅能快速找到较为理想的工艺运行参数组合,同时将提高工艺处理效率.由上述模型结果可以看出,求解得到的最优参数基本都在设计参数范围内,符合实际情况,模型所得结果可以为污水处理厂的运行参数设置提供理论参考,对调试工作具有一定的实际指导意义.
2.3 结果讨论综上,在求解模型获得的最佳运行参数组合中,各运行参数值基本都在经验值范围内,这是符合实际情况的,因此,GA-ANN模型可以用于A2/O工艺运行的参数优化中.但是,神经网络与遗传算法自身具有局限性,此外,A2/O工艺运行的影响因素错综复杂,使得优化过程具有模型与工艺双重多变的特点,在应用模型时特别要注意以下几点:
1) 由于神经网络拟合性能的局限性,BP神经网络的训练预测精度对寻优结果有重大影响.因此,在网络训练时要采用尽量多的训练样本.
2) 影响A2/O工艺运行的参数众多,在建立模型时需要筛选关键性的影响因素,可以运用主成分分析法、聚类分析、多元回归法等数学建模方法.
3) 遗传算法中构造合适的适应度函数非常重要.要综合考虑相应的实际工程要求、水质排放标准、经济成本、运行效益等各个方面.
4) 根据进水水质水平不同,采集更多的水厂样本(利用A2/O工艺,不同地域的水厂),进行模型的优化计算和校核,可以提高模型的精确性和适用范围.
3 结论1) GA-ANN模型可以将众多的工艺运行参数加入到优化过程中,全面综合考察各种关键工艺运行参数影响效果,获得理论上可行的最佳运行参数组合,弥补了传统方法如单一变量法或正交试验法的不足,能为实际的A2/O工艺运行优化提供理论支撑,具有一定的推广应用意义.
2) 模型结构的确定十分重要.例如神经网络模型的输入变量要选取相对较重要、典型的、测量较为方便的运行参数; 输出变量要选取典型的水质指标; 适应度评价时要选取合适的适应度函数,要构造合适的目标函数.
3) GA-ANN模型的建立为优化A2/O工艺的运行参数提供了新思路,对于污水处理厂的调试、运行、确定最优运行参数、提高效率、降低运行成本有重要的实际意义.
| [1] |
王晓莲, 彭永臻.
A2/O法污水生物脱氮除磷处理技术与应用[M]. 北京: 科学出版社, 2009: 21-22.
WANG Xiaolian, PENG Yongzhen. The technology of biological nitrogen and phosphorus removal of A2/O wastewater treatment process and its application[M]. Beijing: Science Press, 2009: 21-22. |
| [2] |
王晓莲, 彭永臻.
A2/O法污水生物脱氮除磷处理技术与应用[M]. 北京: 科学出版社, 2009: 305-306.
WANG Xiaolian, PENG Yongzhen. The technology of biological nitrogen and phosphorus removal of A2/O wastewater treatment process and its application[M]. Beijing: Science Press, 2009: 305-306. |
| [3] |
CHANG Wen, WANG Jun, LI Baihang, et al. Effect of long sludge retention time on biological phosphorus removal in A2/O process[J].
Journal of Residuals Science and Technology, 2015, 12: 67-73.
DOI: 10.12783/issn.1544-8053 |
| [4] |
ZHANG Miao, PENG Yongzhen, WANG Cong, et al. Effect on denitrifying phosphorus removal by optimizing volume ratios in A2/O-biological contact oxidation (A2/O-BCO) process[J].
Journal of Southeast University (Natural Science Edition), 2015, 45(3): 531-538.
|
| [5] |
CHEN Yongzhi, PENG Chengyao, WANG Jianhua, et al. Effect of nitrate recycling ratio on simultaneous biological nutrient removal in a novel anaerobic/anoxic/oxic (A2/O)-biological aerated filter (BAF) system[J].
Bioresource Technology, 2011, 102(10): 5722-5727.
DOI: 10.1016/j.biortech.2011.02.114 |
| [6] |
吴昌永. A2/O工艺脱氮除磷及其优化控制的研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.
WU Changyong. Optimazation of biological nitrogen and phosphorus removal in A2/O wastewater treatment process [D]. Harbin: Harbin Institute of Technology, 2010. http://industry.wanfangdata.com.cn/yj/Detail/Thesis?id=Thesis_D268939 |
| [7] |
李永峰, 潘欣语, 杨建宇. A2/O工艺中HRT对系统脱氮除磷效率的影响[J].
哈尔滨商业大学学报(自然科学版), 2011, 27(4): 567-569.
LI Yongfeng, PAN Xinyu, YANG Jianyu. Effect of HRT on performance of nitrogen and phosphorus removal by A2/O process[J]. Journal of Harbin University of Commerce(Natural Sciences Edition), 2011, 27(4): 567-569. |
| [8] |
刘云雪, 吴建平, 高建磊. 污泥回流比对A2/O工艺脱氮除磷效果的影响[J].
工业用水与废水, 2011, 42(4): 31-33.
LIU Yunxue, WU Jianping, GAO Jianlei. Effect of sludge return ratio on nitrogen and phosphorus removal by A2/O process[J]. Industrial Water & Wastewater, 2011, 42(4): 31-33. |
| [9] |
王建龙, 彭永臻, 高永青. 内循环对A2/O工艺脱氮的影响[J].
北京工业大学学报, 2008, 34(5): 540-542.
WANG Jianlong, PENG Yongzhen, GAO Yongqing. The influence of inner loop of nitrogen of A2/O process[J]. Journal of Beijing University of Technology, 2008, 34(5): 540-542. |
| [10] |
陈昆柏, 宋英琦, 孙培德, 等. A2/O工艺污水处理厂运行参数优化的数值模拟[J].
环境科学学报, 2008, 28(4): 805-806.
CHEN Kunbai, SONG Yingqi, SUN Peide, et al. Simulation and optimization of operational parameters of the A2/O process for wastewater treatment plants[J]. Acta Scientiae Circumstantiae, 2008, 28(4): 805-806. |
| [11] |
马建立, 籍鹏飞, 卢学强, 等. 整体合建A2/O工艺中试试验及参数优化[C]//全国城镇污水处理厂除磷脱氮及深度处理技术交流大会论文集. 天津: 中国给水排水, 2010: 92-93.
MA Jianli, JI Pengfei, LU Xueqiang, et al. Pilot test and parameter optimization of the overall A2/O process construction [C]//The Urban Sewage Treatment Plant Nitrogen and Phosphorus Removal from Deep Processing Technology Exchange Conference Proceedings. Tianjin: China Water & Wastewater, 2010: 92-93. http://d.wanfangdata.com.cn/Conference/7557784 |
| [12] |
AI Hainan, LI Maolin, HE Qiang. Simulation and optimization of denitrifying phosphorus removal in A2/O[J].
Advanced Materials Research, 2012, 374-377: 553-559.
|
| [13] |
PALMER M, FRITZ J. Process design parameters for Chinese municipal wastewater treatment plants[J].
Water Quality Research Journal of Canada, 2004, 39(2): 103-112.
|
| [14] |
LU Peili, LI Zhenliang. Modeling and simulation of the activated sludge process at a full-scale WWTP[J].
Advanced Materials Research, 2012, 599: 505-509.
DOI: 10.4028/www.scientific.net/AMR.599 |
| [15] |
张群英. 神经网络在工业污水处理建模中的应用[J].
计算机仿真, 2012, 29(3): 259-261.
ZHANG Qunying. Research on industrial sewage disposal model based on neural network[J]. Computer Simulation, 2012, 29(3): 259-261. |
| [16] |
胡康, 万金泉, 马邕文, 等. 基于模糊神经网络的A2/O工艺出水氨氮在线预测模型[J].
中国环境科学, 2012, 32(2): 264-266.
HU Kang, WAN Jinquan, MA Yongwen, et al. Online prediction model based on fuzzy neural network for the effluent ammonia concentration of A2/O system[J]. China Environmental Science, 2012, 32(2): 264-266. |
| [17] |
刘载文, 张春芝, 王小艺, 等. 基于遗传算法的污水处理过程优化控制方法[J].
计算机与应用化学, 2007, 24(7): 959-961.
LIU Zaiwen, ZHANG Chunzhi, WANG Xiaoyi, et al. Method of optimal control for wastewater treatment process based on genetic algorithms[J]. Computers and Applied Chemistry, 2007, 24(7): 959-961. |
 2017, Vol. 49
2017, Vol. 49


