无人水面航行器(USV)是近些年伴随着军事需求而新兴发展的产物. USV通过搭载不同类型的传感器或设备模块,可以完成情报搜集、水上监视、无人侦察、反水雷等不同的任务[1].单体USV难以完成日益复杂的任务,从而有必要通过多USV协同作业共同完成任务使命.多USV进行协同作业的首要问题是实现各单体USV精确定位.文献[2]研究了基于长基线的多无人艇协同定位算法,将从艇与两个主艇之间的距离值作为观测量能显著提高定位精度;文献[3]提出一种基于双水听器的多自主航行器协同导航方法;文献[4]提出一种基于Kullback-Leiber距离的单主艇协同导航算法,并通过大量水上试验验证了算法有效性;文献[5-8]则采用相邻时刻的运动矢径作为观测量来实现单主艇协同定位.
协同定位过程的本质是状态预测,而各状态的可观测性及可观测度与系统定位性能存在着紧密关系,所以分析系统的可观测性及可观测度具有重要意义.文献[9]对固定单信标定位系统进行了基于李导数的可观测性分析,表明只要作为量测量的距离矢量方向随时间一直变化,那么定位系统就是可观的,即艇位置信息可估;文献[10]分析了基于距离测量的主从式AUV协同定位系统可观测性,表明从艇控制输入均不为零且主从艇不在同一直线上航行时系统可观,并且分析了不同控制输入下系统的可观测性.值得注意的是,文献[9-10]虽然使用了非线性可观测性分析方法,避免了可观测性条件不充分的问题,但是都没有进一步分析系统可观测度,从而缺少对系统定位性能的定量分析.文献[11]基于条件数分析了多自主水下航行器协同定位系统的可观测度,但是并没有考虑控制输入对协同定位系统可观测度的影响. USV改变控制输入时会影响协同定位系统可观测度的变化,甚至会使系统从可观变为不可观测.所以,脱离控制输入单纯讨论协同定位系统的可观测性及可观测度是不合理的.更为重要的是,上述文献多是在惯性坐标系中进行系统可观测性分析,由于在惯性坐标系中主从USV都存在状态变化,使得主从艇状态无法解耦,从而导致分析过程较为复杂,甚至会导致可观测性分析结论片面的问题.针对以上问题,本文以相对距离为观测量的主从式USV协同定位系统为研究对象,提出在协同坐标系下分析系统可观测性及可观测度,进而定量研究协同定位系统的定位性能.同时,提出通过在协同坐标系中调整控制输入的方式改变系统的可观测性,进而改善系统的定位性能.
1 主从式USV运动学模型由于USV在水面航行,所以主从式USV协同定位系统的定位问题是二维平面内的定位问题.在主从式USV协同定位系统中,主USV搭载高精度导航设备,可以实现精确定位,从USV搭载低精度导航设备,需要获得与主USV间的距离信息并利用数据融合技术来提高自身定位精度. 图 1为基于距离量测的主从式USV协同定位系统,图中ΣI为二维惯性坐标系,定义USV艏艉向与惯性坐标系的XI轴夹角为航向角,以逆时针方向为航向角正向.定义ΣCL为二维协同坐标系,以主USV重心为协同坐标系原点,其x轴方向指向主USV航行方向,y轴垂直于x轴并指向主USV左侧.根据以上定义可以看出,协同坐标系跟随主USV艇体相对惯性坐标系运动,同时主USV相对协同坐标系静止且始终位于协同坐标系原点.主USV在惯性坐标系中的位置为(Xm, Ym),从USV在惯性坐标系中的位置为(X, Y),以从USV的二维位置坐标作状态变量,将惯性坐标系中从USV的状态投影到协同坐标系可得

|
图 1 主从式USV协同定位系统 Figure 1 Leader-follower USVs' cooperative localization system |
| $ \left[ \begin{array}{l} x\left( t \right)\\ y\left( t \right) \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {\cos {\psi _{\rm{m}}}}&{\sin {\psi _{\rm{m}}}}\\ { - \sin {\psi _{\rm{m}}}}&{\cos {\psi _{\rm{m}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {X\left( t \right) - {X_{\rm{m}}}\left( t \right)}\\ {Y\left( t \right) - {Y_{\rm{m}}}\left( t \right)} \end{array}} \right], $ | (1) |
式中ψm为主USV在惯性坐标系中的航向角.进一步,对式(1)两边同时求导可以得到
| $ \begin{array}{l} \left[ \begin{array}{l} \dot x\left( t \right)\\ \dot y\left( t \right) \end{array} \right] = {\left[ {\begin{array}{*{20}{c}} { - \cos {\psi _{\rm{m}}}}&{\sin {\psi _{\rm{m}}}}\\ { - \sin {\psi _{\rm{m}}}}&{ - \cos {\psi _{\rm{m}}}}\\ {\cos {\psi _{\rm{m}}}}&{ - \sin {\psi _{\rm{m}}}}\\ {\sin {\psi _{\rm{m}}}}&{\cos {\psi _{\rm{m}}}} \end{array}} \right]^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {{{\dot X}_{\rm{m}}}\left( t \right)}\\ {{{\dot Y}_{\rm{m}}}\left( t \right)}\\ {\dot X\left( t \right)}\\ {\dot Y\left( t \right)} \end{array}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}} {{\omega _{\rm{m}}}\sin {\psi _{\rm{m}}}}&{{\omega _{\rm{m}}}\cos {\psi _{\rm{m}}}}\\ { - {\omega _{\rm{m}}}\cos {\psi _{\rm{m}}}}&{{\omega _{\rm{m}}}\sin {\psi _{\rm{m}}}}\\ { - {\omega _{\rm{m}}}\sin {\psi _{\rm{m}}}}&{ - {\omega _{\rm{m}}}\cos {\psi _{\rm{m}}}}\\ {{\omega _{\rm{m}}}\cos {\psi _{\rm{m}}}}&{ - {\omega _{\rm{m}}}\sin {\psi _{\rm{m}}}} \end{array}} \right]^T}\left[ {\begin{array}{*{20}{c}} {{X_{\rm{m}}}\left( t \right)}\\ {{Y_{\rm{m}}}\left( t \right)}\\ {X\left( t \right)}\\ {Y\left( t \right)} \end{array}} \right]. \end{array} $ | (2) |
式中ωm为主USV的航向角速度,Ẋm(t)、Ẏm(t)、Ẋ(t)、Ẏ(t)可以分别表示为
| $ \left\{ {\begin{array}{*{20}{c}} {{{\dot X}_{\rm{m}}}\left( t \right) = {V_{\rm{m}}}\cos {\psi _{\rm{m}}},}\\ {{{\dot Y}_{\rm{m}}}\left( t \right) = {V_{\rm{m}}}\sin {\psi _{\rm{m}}},}\\ {\dot X\left( t \right) = V\cos \psi ,}\\ {\dot Y\left( t \right) = V\sin \psi .} \end{array}} \right. $ | (3) |
将式(3)代入式(2)中,可得
| $ \left[ \begin{array}{l} \dot x\left( t \right)\\ \dot y\left( t \right) \end{array} \right] = {\left[ {\begin{array}{*{20}{c}} { - 1}&0\\ {\cos \left( {\psi - {\psi _{\rm{m}}}} \right)}&{\sin \left( {\psi - {\psi _{\rm{m}}}} \right)}\\ {\sin {\psi _{\rm{m}}}}&{\cos {\psi _{\rm{m}}}}\\ { - \cos {\psi _{\rm{m}}}}&{\sin {\psi _{\rm{m}}}}\\ { - \sin {\psi _{\rm{m}}}}&{ - \cos {\psi _{\rm{m}}}}\\ {\cos {\psi _{\rm{m}}}}&{ - \sin {\psi _{\rm{m}}}} \end{array}} \right]^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {{V_{\rm{m}}}}\\ V\\ {{X_{\rm{m}}}{\omega _{\rm{m}}}}\\ {{Y_{\rm{m}}}{\omega _{\rm{m}}}}\\ {X{\omega _{\rm{m}}}}\\ {Y{\omega _{\rm{m}}}} \end{array}} \right], $ | (4) |
进而可以得到从USV在协同坐标系中的速度为
| $ v = \sqrt {v_1^2 + v_2^2} . $ | (5) |
其中v1=ẋ(t),v2=ẏ(t),可由式(4)得到.
从USV在协同坐标系中的航向角记为γ,该航向角定义为从USV的速度矢量与主USV的速度矢量之差与协同坐标系x轴之间的夹角.进一步,可以利用从USV在协同坐标系中的速度v1、v2表示出从USV在协同坐标系中的航向角γ为
| $ \gamma = \left\{ {\begin{array}{*{20}{c}} {\arctan \frac{{{v_2}}}{{{v_1}}},}&{{v_1} > 0;}\\ {\arctan \frac{{{v_2}}}{{{v_1}}} + {\rm{ \mathit{ π} ,}}}&{{v_1} < 0;}\\ {\frac{{\rm{ \mathit{ π} }}}{2},}&{{v_1} = 0,{v_2} > 0;}\\ { - \frac{{\rm{ \mathit{ π} }}}{2},}&{{v_1} = 0,{v_2} < 0.} \end{array}} \right. $ | (6) |
至此,将主从USV的位置、速度及航向角全部投影到协同坐标系中.在协同坐标系中,主艇的位置始终为坐标系原点,从而可以将其看作是一个固定信标,这样惯性坐标系中主从USV间的相对运动信息都转化到协同坐标系中的从USV上.基于这种建模方式进行系统可观测性及可观测度分析可以大大简化分析过程,而且还充分考虑了主从USV的相对速度大小、相对航向及相对位置对系统可观测性的影响,使得可观测性条件的充分性得到保障.
2 协同定位系统性能分析系统可观测是其状态可估的前提,不可观测系统的定位误差将随时间的推移而不断增长,并最终使协同定位系统失去稳定性[12].系统可观测度是定量的描述系统的可观测情况,系统可观测度为0时系统不可观测,可观测度越大则系统的可观测性越好.所以系统的定位性能与其可观测性及可观测度度有着紧密的联系,可以通过分析其可观测性及可观测度来分析系统的性能.主从式USV协同定位系统观测量是主从USV间的相对距离,所以观测方程为
| $ h\left( x \right) = \sqrt {{{\left( {X - {X_{\rm{m}}}} \right)}^2} + {{\left( {Y - {Y_{\rm{m}}}} \right)}^2}} = \sqrt {{x^2} + {y^2}} . $ | (7) |
显然观测方程是一个非线性方程,为了更加准确地分析系统可观测性,本文使用李导数来对其可观测性进行分析.本文在第1节建立的基于协同坐标系的主从式USV运动模型基础上分析系统可观测性及可观测度,根据系统可观测性的李导数判定方法,首先将从USV在协同坐标系中的状态方程表示成如下连续形式:
| $ \mathit{\boldsymbol{\dot x}} = f\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}}} \right), $ | (8) |
其中
| $ f = \left( {\begin{array}{*{20}{c}} {{f_1}}\\ {{f_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {v\cos \gamma }\\ {v\sin \gamma } \end{array}} \right). $ | (9) |
观测方程的零阶李导数就是方程本身,可以写作
| $ {L^0}h\left( \mathit{\boldsymbol{x}} \right) = \sqrt {{x^2} + {y^2}} . $ | (10) |
求解L0h(x)关于USV状态量的梯度,得
| $ \nabla {L^0}h\left( x \right) = \left[ {\begin{array}{*{20}{c}} {\frac{x}{{\sqrt {{x^2} + {y^2}} }}}&{\frac{y}{{\sqrt {{x^2} + {y^2}} }}} \end{array}} \right], $ | (11) |
进而求得一阶李导数的梯度为
| $ \nabla {L^1}h = \left[ {\begin{array}{*{20}{c}} {\frac{{{v_1}{y^2} - {v_2}xy}}{{{{\left( {\sqrt {{x^2} + {y^2}} } \right)}^3}}}}&{\frac{{{v_2}{x^2} - {v_1}xy}}{{{{\left( {\sqrt {{x^2} + {y^2}} } \right)}^3}}}} \end{array}} \right], $ | (12) |
那么可观测性矩阵可以写作
| $ \mathit{\boldsymbol{O}} = \left[ {\begin{array}{*{20}{c}} {\frac{x}{{\sqrt {{x^2} + {y^2}} }}}&{\frac{y}{{\sqrt {{x^2} + {y^2}} }}}\\ {\frac{{{v_1}{y^2} - {v_2}xy}}{{{{\left( {\sqrt {{x^2} + {y^2}} } \right)}^3}}}}&{\frac{{{v_2}{x^2} - {v_1}xy}}{{{{\left( {\sqrt {{x^2} + {y^2}} } \right)}^3}}}} \end{array}} \right]. $ | (13) |
可观测性矩阵的行列式值为
| $ \det \mathit{\boldsymbol{O}} = \frac{{{v_1}y - {v_2}x}}{{{x^2} + {y^2}}}. $ | (14) |
根据线性代数可知,当矩阵行列式不等于0时,即只要v1y-v2x≠0,那么可观测性矩阵满秩,此时系统完全可观.根据式(14)可知,当det O=0时,可分为以下3种情况:1)从USV在协同坐标系ΣCL中的原点位置,考虑到坐标系原点固连在主USV艇体重心处,所以在实际运动中不可能出现这种情况. 2)从USV在协同坐标系ΣCL中的速度为0,这种情况意味着主从USV相对静止,即两者速度大小相等,方向相同. 3)更一般的情况,可由式
通过以上分析可知,当主从式USV协同定位系统满足以上3种情况时,系统不可观,将后两种情况定义为主从式USV协同定位系统的不可观测路径.除此之外,主从式USV协同定位系统都可观.但是,系统是否可观只是从定性角度反映了观测量是否具备解算出系统状态量的能力,并不能描述其性能的好坏.在实际应用中,仅仅明确系统是否可观往往是不够的.对于完全可观的系统,尚存在可观测程度的问题.如果系统可观测矩阵性态不好,那么即使系统完全可观,也有可能造成系统方程的病态性.另外,考虑到单纯依靠距离观测的协同定位系统观测信息量有限,往往更关心的是系统可观测性大小的条件性变化,即系统在何种条件下可观测性强,何种条件下可观测性弱,只有这样才能够在实际应用过程中有目的的去设计合理的协同定位方案(包括队形编排、航路机动以及协同规则等),从而保证协同定位性能.为进一步考察系统状态量的估计精度,通过矩阵条件数理论对系统可观测度作进一步分析.常用的关于p范数‖·‖p的条件数标记为condAp,一般称condA2为谱条件数.根据矩阵条件数理论,条件数小的矩阵称为“良性”矩阵,反之称为“病态”矩阵.系统可观测性矩阵的条件数越大,系统的可观测程度越差;如果系统可观测性矩阵的条件数无穷大,则系统不可观测;反之,系统可观测矩阵的条件数越接近1,系统的可观测性最好.由于矩阵条件数是一个≥1的正数,不妨定义可观测度D为可观测矩阵O条件数的倒数,即
| $ D = {\left( {{\rm{cond}}\;\mathit{\boldsymbol{O}}} \right)^{ - 1}}. $ | (15) |
根据以上分析,D可表示为
| $ D = \frac{{\min \left( {v,\left| {\frac{{{x^2} + {y^2}}}{{y\cos \gamma - x\sin \gamma }}} \right|} \right)}}{{\max \left( {v,\left| {\frac{{{x^2} + {y^2}}}{{y\cos \gamma - x\sin \gamma }}} \right|} \right)}}. $ | (16) |
由上式可知,当
| $ {x^2} + {y^2} + vx\sin \gamma - vy\cos \gamma = 0, $ | (17) |
| $ {x^2} + {y^2} - vx\sin \gamma + vy\cos \gamma = 0. $ | (18) |
根据平面几何知识可知,式(17)表示的是以(-v·sin γ/2, v·cos γ/2)为圆心,v/2为半径的圆,式(21)表示的是以(v·sin γ/2, -v·cos γ/2)为圆心,v/2为半径的圆,也就是说,当从USV在协同坐标系中的位置在式(17)、(18)表示的两个圆中任意一个上时,系统可观测度最大为1.
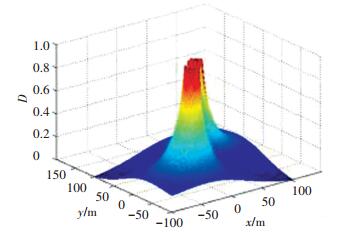
为了更加清晰的观察从艇在协同坐标系中的速度v以及航向角γ对系统可观测度的影响,设置两组仿真,第1组仿真中从艇速度v不变,改变从艇航向角γ,观察不同航向角下可观测度的分布情况,仿真结果如图 2、3所示;第2组仿真中,从艇航向角γ不变,改变从艇速度v,观察不同速度下可观测度的分布情况,仿真结果如图 4所示.

|
图 2 可观测度三维图 Figure 2 Three dimensional graph of observable measure |
|
图 3 观测度三维图 Figure 3 Three dimensional graph of observable measure |
|
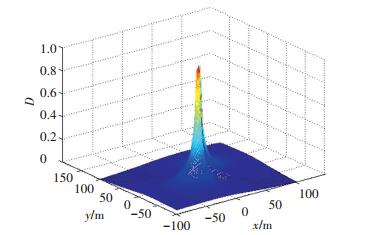
图 4 观测度三维图 Figure 4 Three dimensional graph of observable measure |
当从USV在协同坐标系中的速度v=20 m/s,航向角γ=0°时,可观测度随从USV位置变化如图 2所示.当从USV在协同坐标系中的速度v=20 m/s,航向角γ=135°时,可观测度随从USV位置变化如图 3所示.当从USV在协同坐标系中的速度v=5 m/s,航向角γ=135°时,可观测度随从USV位置变化如图 4所示.
上面3组图中的x轴、y轴坐标表示从USV在协同坐标系中的坐标,D轴表示系统可观测度.可以看出,系统的控制输入对可观测度有影响,那么针对不可观测路径或可观测度低的路径,可以通过改变系统控制输入,使从USV在协同坐标系中的位置位于可观测度高的区域,从而改善系统定位性能,具体调整方法可根据实际情况和任务需求利用式(19)进行调整.举例说明:当任务需要主从USV同时驶向某地时,各USV往往会以大致相同的速度航行.根据前述分析可知,这种运动方式对应不可观测路径(2)的情况,从而导致系统不可观.在这种情况下,可以通过改变系统控制输入达到改善系统可观性的目的,即选择主从USV中任意一个进行变速运动,使主从USV间始终存在相对运动,从而使得从USV在协同坐标系中处于较高可观测度的位置,进而可以改善系统定位性能.针对不可观测路径(3)的情况,由于此时满足式tan γ=y/x使得系统不可观测,此时可通过圆形机动来快速提高系统可观测度,圆形机动轨迹可以减小速度与位移分量比例的相似程度,也就使得tan γ≠y/x,从而达到提高系统可观测度,改善系统定位性能的目的.
通常情况下,USV的航向根据任务需要确定,为了使系统可观测度提高,可以在航向不变的情况下改变速度大小,根据式(16),可以推导出
| $ v = \left( {{x^2} + {y^2}} \right)/\left| {y\cos \gamma - x\sin \gamma } \right|. $ | (19) |
速度越接近式(19),系统的可观测度越大.当速度满足式(19)时,系统可观测度为1.在USV协同定位时,由于实际系统的条件限制并不一定能满足式(19),只能使从USV在协同坐标系中的速度尽可能接近式(19),来提高系统可观测度.
3 仿真与实验 3.1 仿真试验为验证本文分析的正确性,首先利用MATLAB进行仿真试验,试验主要针对不可观测路径进行仿真;在此基础上,进行调整系统控制输入使不可观测路径变为可观测路径的仿真验证.
3.1.1 不可观测路径仿真当协同定位系统满足det O=(v1y-v2x)/(x2+y2)=0时,系统不可观测,对第二节分析中的不可观测路径(2)和不可观测路径(3)进行仿真.
1) 主从USV相对静止.主USV初始状态为(-1, 1),航向为0°,速度为2 m/s;从USV初始状态为(20, -20),初始状态估计值为(120, -120),航向为0°,速度为2 m/s,其余仿真条件相同,此时主从USV相对静止,系统不可观测,仿真结果如图 5所示.

|
图 5 协同定位系统相对静止路径 Figure 5 Relative stationary path of cooperative localization system |
图 5(a)中3条曲线分别为主USV轨迹,从USV真实轨迹以及从USV的EKF滤波轨迹,图 5(b)为从USV定位误差,从图中可以看到定位误差始终在40 m附近,图 5(c)为系统可观测度随时间变化曲线,从图中可以看出系统可观测度一直为0.当主从艇相对静止时,系统不可观测,滤波轨迹始终与真实轨迹存在较大误差,与前文理论分析结论一致.
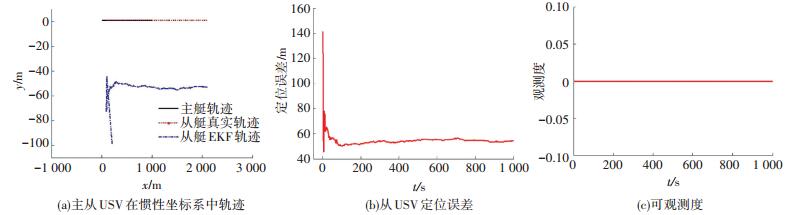
2) 主从USV连线与x轴夹角为航向角.主从USV连线即从USV与协同坐标系原点连线,当主从USV连线与协同你坐标系x轴夹角为航向角时,根据前文分析可知此时系统不客观.主USV初始状态为(-1, 1),航向为0°,速度为1 m/s;从USV初始状态为(100, 1),初始状态估计值为(200, -99),航向为0°,速度为2 m/s,其余仿真条件与3.1.(1)节相同,仿真结果如图 6所示.
|
图 6 协同定位系统过协同原点路径 Figure 6 The path through the origin of the cooperative coordinate system ofcooperative localization system |
图 6(a)中3条曲线分别为主USV轨迹,从USV真实轨迹以及从USV的EKF滤波轨迹,图 6(b)为从USV定位误差,从图中可以看出始终存在70 m左右的定位误差,图 6(c)为系统可观测度,从图中可以看出可观测度一直为0.从仿真结果可以看出,相对运动轨迹经过协同坐标系ΣCL坐标系原点时,系统不可观测,滤波轨迹与真实轨迹有很大差距,与前文理论分析结论一致.
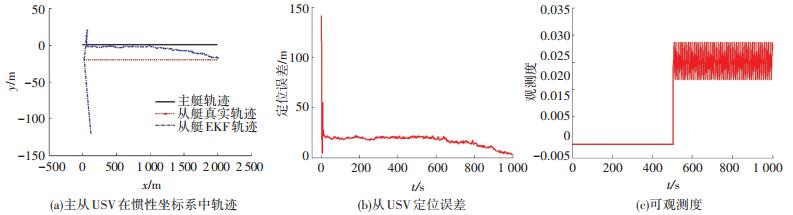
3.1.2 不可观测路径调整控制输入后仿真1) 针对主从USV相对静止路径.为了验证改变控制输入可以提高系统定位性能,前500 s仿真条件与3.1.1条件相同,此时主从USV速度大小相等、方向相同,即主从艇相对静止,系统不可观;500 s之后,使从USV停止5 s,运行5 s,且运行速度设置为4 m/s,此时主从USV始终存在相对运动,系统可观测,仿真结果如图 7所示.
|
图 7 调整控制输入的协同定位系统 Figure 7 Adjust the control input ofcooperative localization system |
从图 7(c)可以看出系统观测度在调整控制输入后有显著提高,在调整前系统观测度为0,即系统不可观;500 s后,从USV速度开始变化,此时由于速度的变化使得主从USV相对位置发生变化,引起可观测度上下振荡变化.从图 7(b)也可以看出在速度调整前系统定位误差较大,在调整速度后定位误差逐渐收敛,从而验证了本文所提方法的有效性.
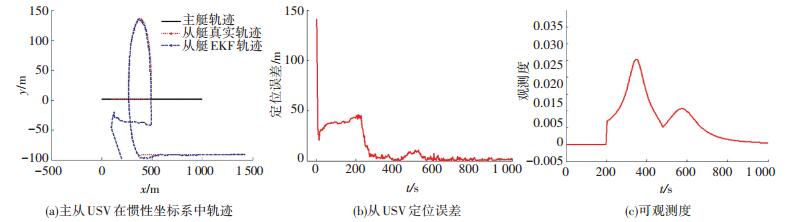
2) 针对主从USV连线与x轴夹角为航向角路径.主USV初始状态为(-1, 1),航向为0°,速度为2 m/s;从USV初始状态为(100, 1),初始状态估计值为(200, -99),速度为2 m/s,前200 s航向为0°,此时由于主从USV连线与协同坐标系x轴夹角与航向角相同,导致系统不可观测.为改善系统定位性能,使从艇在200~210 s之间航向为90°,210 s到480 s开始作圆形机动路径,480 s后航向仍为0°,仿真结果如图 8所示.
|
图 8 调整控制输入的协同定位系统 Figure 8 Adjust the control input ofcooperative localization system |
从图 8(c)可以看出系统在调整控制输入后可观测度有显著的增加,在前200 s系统没有调整控制输入,此时系统的观测度为0,系统不可观,从图 8(b)可以看出在速度调整前系统的定位误差很大;在200 s后系统调整控制输入,可以看出调整控制输入后系统可观测度显著提高,定位误差也逐渐减小,验证了本文所提方法的有效性.
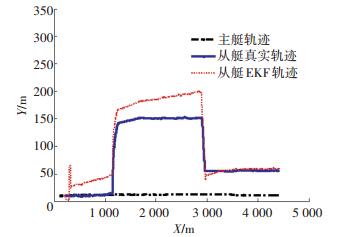
3.2 USV水上实验为进一步验证本文所得出的结论在实际系统中的有效性,在无锡太湖水域进行了协同定位湖上验证性试验.主从USV均配备GPS,从USV配备GPS是为了给后续数据处理过程中提供位置基准.试验过程中以主艇高精度的实时GPS位置信息为参考基准,基于水声通信设备实现主从艇间参考信息的传递以及相对距离信息的观测,进而实现对从艇航位推算误差的协同校正.从艇的航位推算位置是基于DVL提供的绝对速度信息以及磁罗经提供的航向信息推算得到的.水声通信设备是实现航行器协同定位的关键,试验采用水声通信设备构建水声通信网络,实现主从艇相互间相对距离的测量以及参考信息的传递.试验中GPS定位精度为2.5 m(RMS),测速精度0.1 m/s,更新频率为10 Hz,磁罗经方位精度为2°,DVL测速精度为0.1%.试验过程中主艇以5 s固定时间间隔向从艇发送自身带标识符的GPS位置信息以及二者间相对距离量测信息,辅助从艇进行导航误差的协同校正.主从USV在水上共进行了40 min试验,试验中主从USV的轨迹如图 9所示.首先主从USV同向航行,前后相距大约100 m,主USV始终朝着东向航行,从USV在前8 min左右向东以大于主USV的速度航行,从USV航行约8 min后转向,以90°航向角航行,航行约2 min后,与主USV同向航行,航速与主艇大致相同,航行约14 min后,转向朝着主USV航行约4 min,然后再次与主USV同向航行直至实验结束,但速度时刻变化.
|
图 9 水上试验轨迹 Figure 9 Experimental trajectory on water |
按照前文分析,前8 min主从USV连线与协同坐标系x轴夹角为从USV在协同坐标系中航向角,则系统不可观;从第8 min到第10 min是可观测路径;从第10 min到第24 min主从USV同向同速航行,主从USV相对静止,系统不可观;从第24 min到第28 min从USV满足可观测条件;28 min后,由于从USV速度时刻变化,使得其始终可观测.从USV定位误差及观测度如图 10所示,可以看出试验结果与本文分析相符,由于实际系统中的噪声不是仿真实验中的零均值高斯噪声,导致从USV在不可观测时误差逐渐增大,在第8 min到第10 min时虽然系统可观测,但是由于观测性很小,在图 10(b)中只有一个小的尖峰,而且时间很短,所以此时误差下降不多,在系统可观测时误差稳定在10 m左右,验证了本文分析的正确性.

|
图 10 水上试验从USV定位误差及观测度 Figure 10 Positioning Error andObservability of follower USV in water experiment |
1) 两种不可观测路径:从USV在协同坐标系坐标系中速度为零时系统不可观;协同坐标系中主从USV连线与x轴夹角与航向角相同时系统不可观测.
2) 主从式USV协同定位系统可观测度可由式(16)表示.从USV在协同坐标系中速度大小决定较高可观测度的范围大小,速度越大,高可观测度范围越大,γ决定不可观测范围方向.
3) 在USV协同定位时,可以根据下式v=(x2+y2)/|ycosγ-xsin γ|来改变USV速度,达到提高系统可观测度、减小定位误差的目的.
| [1] |
YAN Rujian, PANG Shuo, SUN Hanbing. Development and missions of unmanned surface vehicle[J].
Journal of Marine Science and Application, 2010, 9(1): 451-457.
|
| [2] |
张立川, 徐德民, 刘明雍, 等. 基于移动长基线的多AUV协同导航[J].
机器人, 2009, 31(6): 581-585, 593.
ZHANG Lichuan, XU Demin, LIU Mingyong, et al. Cooperative navigation of multiple AUVs using moving long baseline[J]. Robot, 2009, 31(6): 581-585, 593. |
| [3] |
张立川, 徐德民, 刘明雍, 等. 基于双水听器的多自主水下航行器协同导航方法[J].
系统工程与电子技术, 2011, 33(7): 1603-1606.
ZHANG Lichuan, XU Demin, LIU Mingyong, et al. Cooperative navigation for multiple autonomous underwater vehicles based on two hydrophones[J]. Systems Engineering and Electronics, 2011, 33(7): 1603-1606. |
| [4] |
CURCIOO J, LEONARD J, VAGANAY J, et al. Experiments in moving baseline navigation using autonomous surface craft[C]//Proceedings of MTS/IEEE OCEANS. Washington DC: IEEE, 2005:730-735.
http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1639839
|
| [5] |
BAHR A. Cooperative localization for autonomous underwater vehicles [R]. Cambridge: Massachusetts Institute of Technology, 2009.
|
| [6] |
ZHANG Lichuan, XU Demin, LIU Mingyong, et al. Cooperative navigation and location for multiple UUVs[J].
Journal of Marine Science and Application, 2009, 8(3): 216-221.
DOI: 10.1007/s11804-009-8059-3 |
| [7] |
姚尧, 徐德民, 张立川, 等. 通信延迟下的多UUV协同定位—基于航迹预测的实时更新算法[J].
机器人, 2011, 33(1): 161-168.
YAO Yao, ZHANG Lichuan, XU Demin, et al. Cooperative localization of multiple UUVs with communication delays—a real-time update method based on path prediction[J]. Robot, 2011, 33(1): 161-168. |
| [8] |
李闻白, 刘明雍, 李虎雄, 等. 基于单领航者相对位置测量的多AUV协同导航系统定位性能分析[J].
自动化学报, 2011, 37(6): 24-73, 76.
LI Wenbai, LIU Mingyong, LI Huxiong, et al. Localization performance analysis of cooperative navigation system for multiple AUVs based on relative position measurements with a single leader[J]. Acta Automatica Sinica, 2011, 37(6): 24-73, 76. |
| [9] |
PAPADOPOULOS G. Underwater vehicle localization using range measurements [D].Cambridge: Massachusetts Institute of Technology, 2010.
http://agris.fao.org/openagris/search.do?recordID=AV2012054371
|
| [10] |
房新鹏, 严卫生, 李俊兵. 基于距离量测的主从式AUV协同定位系统观测性研究[J].
西北工业大学学报, 2012, 30(4): 547-552.
FANG Xinpeng, YAN Weisheng, LI Junbing, et al. Observability analysis of leader-follower cooperative localization system based on relative position measurements[J]. Journal of Northwestern Polytechnical University, 2012, 30(4): 547-552. |
| [11] |
马朋, 张福斌, 徐德民, 等. 基于条件数的多自主水下航行器协同定位系统可观测度分析[J].
兵工学报, 2015, 01(1): 138-143.
MA Peng, ZHANG Fubin, XU Demin, et al. Observability Analysis of cooperative localization system for MAUV based on condition number[J]. ACTA ARMAMENTARII, 2015, 01(1): 138-143. |
| [12] |
GADRE A.Observability analysis in navigation systems with an underwater vehicle application [D].Montgomery: Virginia Polytechnic Institute and State University, 2007.
http://agris.fao.org/agris-search/search.do?recordID=AV2012098573
|
 2017, Vol. 49
2017, Vol. 49


