航天器高精度姿态稳定与跟踪控制是执行在轨操作的基础，随着航天器在空间探测、通信、导航等领域的广泛应用，航天器的姿态控制问题吸引了众多国内外学者的关注^[1-2].考虑航天器飞行过程的外界干扰和系统不确定，滑模控制作为一种鲁棒控制方法，在航天器姿态控制系统中受到广泛关注.线性滑模首先在航天器姿态控制系统中获得应用，包括单星级航天器姿态跟踪控制和航天器编队姿态协调控制^[3-4].由于终端滑模具有更高的控制精度和更快的响应特性，在航天器姿态控制获得了更广泛的研究和应用^[5-6].

同目前大多数航天器姿态控制研究相同，上述航天器姿态控制系统均采用全状态反馈.在控制器设计中既利用航天器姿态信息，同时也需要航天器角速度信息.但在实际工程应用中，由于角速率陀螺损坏或者研制成本约束，导致角速度信息无法获取，只能利用输出反馈技术进行航天器姿态控制器设计.针对这一问题，文献[7]首先提出的是滤波器算法，利用航天器姿态四元数或MRPs(修改罗德里格斯参数)作为滤波器输入，从而获得对应导数信息并进行反馈控制，此算法在航天器姿态跟踪及编队姿态协调控制中获得了较多应用^[8-9].除此之外，状态观测器设计也是解决姿态输出反馈的一种重要手段，其中包括全阶状态观测器^[10]、降阶状态观测器^[11]、扩张状态观测器^[12]等，通过状态观测器的设计，也能得到对应的姿态导数信息.但是，上述滤波器技术和观测器技术都只能实现对姿态导数的渐进估计.为进一步减小估计时间，提高估计精度，文献[13-14]基于几何齐次性理论设计了有限时间状态观测器，能够实现对MRPs导数的有限时间估计，但观测精度会受到外界扰动及系统不确定影响.文献[15-16]基于终端滑模设计了有限时间观测器，但需要系统综合不确定和未知状态导数上界已知.并且上述有限时间观测器都是基于姿态动力学模型的，只能实现对四元数或MRPs导数的估计，无法获取角速度估计值.

当前在滑模姿态控制研究中，一般采用带有符号函数的鲁棒项对系统外界扰动和不确定进行处理，从而使控制输入产生抖振.为减小控制器抖振，同时对系统综合不确定进行处理，采用自适应控制，并且在航天器姿态跟踪控制中获得较多应用^[17].但在这些自适应滑模控制器设计中，由于引入了符号函数，使得控制输入是不连续的，不可避免会产生抖振.干扰观测器技术是进行航天器鲁棒姿态控制的另一种手段，能够观测出系统综合不确定信息，同时抑制抖振.文献[18]设计了扩张状态观测器来进行航天器姿态系统综合不确定的估计，但只得到了渐进稳定结果.文献[19]设计了一种终端滑模干扰观测器，能够实现对系统不确定的有限时间精确估计.高阶滑模干扰观测器^[20]也可用来进行系统不确定的有限时间估计，但这些有限时间干扰观测器均需要系统综合不确定导数或Lipschitz常数已知.本文研究了角速度不可测的航天器有限时间姿态跟踪控制.首先，设计了无需模型的改进自适应超螺旋滑模状态观测器，在有限时间内实现对四元数导数的估计，进而结合扩维姿态运动学方程得到角速度信息；然后，提出了一种新的有限时间自适应干扰观测器，并进行了有限时间姿态跟踪控制器设计.设计的两种观测器无需未知状态导数和综合不确定导数上界已知，同时控制器能较好实现抖振抑制.

1 刚体航天器非线性姿态模型

航天器在空间进行姿态控制过程中，有多个坐标系需要明确.定义F_B为本体固连坐标系，F_I为惯性坐标系，F_D为期望姿态坐标系，采用单位四元数描述航天器姿态，则刚体航天器运动学与动力学方程^[4]为

$ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot q}}}_v} = \frac{1}{2}\left( {{q_0}{\mathit{\boldsymbol{I}}_3} + \mathit{\boldsymbol{q}}_v^ \times } \right)\mathit{\boldsymbol{w}},\\ {{\dot q}_0} = - \frac{1}{2}\mathit{\boldsymbol{q}}_v^{\rm{T}}\mathit{\boldsymbol{w}}. \end{array} \right. $

(1)

$ \mathit{\boldsymbol{J\dot w}} = - {\mathit{\boldsymbol{w}}^ \times }\mathit{\boldsymbol{Jw}} + \mathit{\boldsymbol{u}} + \mathit{\boldsymbol{d}}. $

(2)

其中：q=[q₀ q₁ q₂ q₃]^T=[q₀ q_v^T]^T为航天器本体F_B相对于F_I的单位四元数，w∈R³为F_B相对于F_I的角速度，u∈R³为控制输入力矩，d∈R³为外界环境干扰，J=J₀+ΔJ是航天器惯性矩阵，其中J₀和ΔJ分别为标称部分和不确定部分，q_v^×∈R^3×3是斜对角矩阵并满足

$ \mathit{\boldsymbol{q}}_v^ \times = \left[ {\begin{array}{*{20}{c}} 0&{ - {q_3}}&{{q_2}}\\ {{q_3}}&0&{ - {q_1}}\\ { - {q_2}}&{{q_1}}&0 \end{array}} \right]. $

在姿态跟踪控制过程中，定义期望姿态四元数为q_d=[q_d0 q_d1 q_d2 q_d3]^T=[q_d0 q_dv^T]^T，期望角速度为w_d，满足

$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{q}}_{ev}} = {\mathit{\boldsymbol{q}}_{d0}}{\mathit{\boldsymbol{q}}_v} - \mathit{\boldsymbol{q}}_{dv}^ \times {\mathit{\boldsymbol{q}}_v} - {\mathit{\boldsymbol{q}}_0}{q_{dv}},\\ {q_{e0}} = \mathit{\boldsymbol{q}}_{dv}^{\rm{T}}{\mathit{\boldsymbol{q}}_v} + {q_0}{q_{d0}},\\ {\mathit{\boldsymbol{w}}_e} = \mathit{\boldsymbol{w}} - \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{w}}_d}. \end{array} \right. $

(3)

其中R为由F_D到F_B的旋转矩阵，并满足

$ \mathit{\boldsymbol{R}} = \left( {q_{e0}^2 - \mathit{\boldsymbol{q}}_{ev}^{\rm{T}}{\mathit{\boldsymbol{q}}_{ev}}} \right){I_3} + 2{\mathit{\boldsymbol{q}}_{ev}}\mathit{\boldsymbol{q}}_{ev}^{\rm{T}} - 2q_{e0}^2\mathit{\boldsymbol{q}}_{ev}^ \times . $

(4)

从而得到姿态跟踪误差动力学^[4]为

$ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot q}}}_{ev}} = \frac{1}{2}\left( {{q_{e0}}{\mathit{\boldsymbol{I}}_3} + \mathit{\boldsymbol{q}}_{ev}^ \times } \right){\mathit{\boldsymbol{w}}_e},\\ {{\dot q}_{e0}} = - \frac{1}{2}\mathit{\boldsymbol{q}}_{ev}^{\rm{T}}{\mathit{\boldsymbol{w}}_e}. \end{array} \right. $

(5)

$ \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot w}}}_e} = - {\mathit{\boldsymbol{w}}^ \times }\mathit{\boldsymbol{Jw}} + \mathit{\boldsymbol{J}}\left( {\mathit{\boldsymbol{w}}_e^ \times \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{w}}_d} - \mathit{\boldsymbol{R}}{{\mathit{\boldsymbol{\dot w}}}_d}} \right)\mathit{\boldsymbol{ + u}} + \mathit{\boldsymbol{d}}. $

(6)

2 有限时间角速度估计

为实现对不可测的角速度进行有限时间估计，首先设计改进自适应超螺旋滑模状态观测器，在有限时间内实现对四元数导数的估计，而后对姿态运动学方程进行扩维，并计算出对应的角速度值.

引理1^[21]  考虑如下非线性系统

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot x = }} - \alpha \frac{\mathit{\boldsymbol{x}}}{{{{\left\| \mathit{\boldsymbol{x}} \right\|}^{1/2}}}} + \mathit{\boldsymbol{z}},\\ \mathit{\boldsymbol{\dot z}} = - \frac{\beta }{2}\frac{\mathit{\boldsymbol{x}}}{{\left\| \mathit{\boldsymbol{x}} \right\|}} + \mathit{\Delta} . \end{array} \right. $

(7)

其中‖Δ‖≤δ，存在任意正常数k₁, k₂，ε，满足

$ \left\{ {\begin{array}{*{20}{c}} {\dot \alpha = \left\{ \begin{array}{l} {k_1}\sqrt {{k_2}/2} ,\;\;\;\mathit{\boldsymbol{x}} \ne 0;\\ \;\;\;\;\;\;0,\;\;\;\mathit{\boldsymbol{x}} = 0; \end{array} \right.}\\ {\dot \beta = 2\varepsilon \alpha .} \end{array}} \right. $

(8)

则x和ẋ在有限时间收敛到零.

假设1  航天器飞行过程中，姿态四元数q二阶可微，并满足$\left\| {\ddot {\boldsymbol{q}}} \right\| \le l $，其中l>0为未知常数.

基于上述引理和假设，设计的改进自适应超螺旋滑模状态观测器为

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot {\hat q} = }} - {\alpha _1}\frac{\mathit{\boldsymbol{e}}}{{{{\left\| \mathit{\boldsymbol{\theta }} \right\|}^{1/2}}}} + \mathit{\boldsymbol{v}},\\ \mathit{\boldsymbol{\dot v}} = - \frac{{{\beta _1}}}{2}\frac{\mathit{\boldsymbol{e}}}{{\left\| \mathit{\boldsymbol{\theta }} \right\|}}. \end{array} \right. $

(9)

其中e=$\hat {\boldsymbol{q}}-\boldsymbol{q} $，$\left\| \theta \right\| = \left\{ \begin{array}{l} \left\| \boldsymbol{e} \right\|,\left\| \boldsymbol{e} \right\| > \varphi ;\\ \varphi ,\left\| \boldsymbol{e} \right\| \le \varphi . \end{array} \right. $. φ>0为设计的边界层，自适应增益为

$ \left\{ {\begin{array}{*{20}{c}} {{{\dot \alpha }_1} = \left\{ {\begin{array}{*{20}{c}} {{{\bar k}_1}\sqrt {{{\bar k}_2}/2} ,\;\;\;\left\| \mathit{\boldsymbol{e}} \right\| > \varphi ;}\\ {0,\;\;\;\left\| \mathit{\boldsymbol{e}} \right\| \le \varphi ;} \end{array}} \right.}\\ {{{\dot \beta }_1} = 2\bar \varepsilon {\alpha _1}.} \end{array}} \right. $

(10)

k₁，k₂和$\bar \varepsilon $为任意正常值.

由(9)可得状态观测器误差方程为

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot e = }} - {\alpha _1}\frac{\mathit{\boldsymbol{e}}}{{{{\left\| \mathit{\boldsymbol{\theta }} \right\|}^{1/2}}}} + \mathit{\boldsymbol{\bar v}},\\ \mathit{\boldsymbol{\dot {\bar v}}} = - \frac{{{\beta _1}}}{2}\frac{\mathit{\boldsymbol{e}}}{{\left\| \mathit{\boldsymbol{\theta }} \right\|}} - \mathit{\boldsymbol{\ddot q}}. \end{array} \right. $

(11)

由引理1容易得到，所设计的改进自适应超螺旋滑模观测器(9)、(10)能保证$\hat {\boldsymbol{q}} $和$\dot {\hat {\boldsymbol{q}}} $在有限时间内收敛到q和$\dot {\boldsymbol{q} }$的邻域内.

注1  超螺旋滑模观测器(9)相比于式(7)，其主要改进之处为将式(7)中的奇异点采用边界层进行代替.虽然式(7)能实现对未知状态的精确估计，但会导致抖振，即使$\hat {\dot {\boldsymbol{q}}} $含有微小抖振，经过微分之后也会对估计角速度导数产生较大影响，从而影响控制精度.故改进滑模观测器设计为式(9)形式.

注2  所设计的滑模观测器(9)相比于滤波器算法^[7-9]和渐进状态观测器^[10-12]，能够实现对未知状态的有限时间估计；相比于基于几何齐次性和终端滑模的观测器^[13-16]，式(9)不依赖于姿态动力学模型，同时也无需系统不确定和未知状态导数上界已知.

通过式(9)可得出$\hat {\boldsymbol{q}} $和$\dot {\hat {\boldsymbol{q}}} $具体数值，进而可以进行角速度的计算.将姿态运动学方程展开为

$ \left[ {\begin{array}{*{20}{c}} { - 2{{\dot q}_0}}\\ {2{{\dot q}_1}}\\ {2{{\dot q}_2}}\\ {2{{\dot q}_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{q_1}}&{{q_2}}&{{q_3}}\\ {{q_0}}&{ - {q_3}}&{{q_2}}\\ {{q_3}}&{{q_0}}&{ - {q_1}}\\ { - {q_2}}&{{q_1}}&{{q_0}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{w_1}}\\ {{w_2}}\\ {{w_3}} \end{array}} \right] = A\left[ {\begin{array}{*{20}{c}} {{w_1}}\\ {{w_2}}\\ {{w_3}} \end{array}} \right]. $

(12)

由于A∈R^4×3不是方阵，故不能对上式进行矩阵逆操作，无法直接求出角速度信息.为了实现对角速度的求解，将上式矩阵进行扩维，得到如下矩阵

$ \left[ {\begin{array}{*{20}{c}} { - 2{{\dot q}_0}}\\ {2{{\dot q}_1}}\\ {2{{\dot q}_2}}\\ {2{{\dot q}_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{q_1}}&{{q_2}}&{{q_3}}&{ - {q_0}}\\ {{q_0}}&{ - {q_3}}&{{q_2}}&{{q_1}}\\ {{q_3}}&{{q_0}}&{ - {q_1}}&{{q_2}}\\ { - {q_2}}&{{q_1}}&{{q_0}}&{{q_3}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{w_1}}\\ {{w_2}}\\ {{w_3}}\\ 0 \end{array}} \right] = \bar A\left[ {\begin{array}{*{20}{c}} {{w_1}}\\ {{w_2}}\\ {{w_3}}\\ 0 \end{array}} \right]. $

(13)

可知A∈R^4×4为四维方阵，同时$\det \left( {\boldsymbol{\overline A} } \right) = \sum\limits_{i = 0,1,2,3} {q_i^2} $，故可对上式进行矩阵逆操作，得到

$ \left[ {\begin{array}{*{20}{c}} {{w_1}}\\ {{w_2}}\\ {{w_3}}\\ 0 \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {{q_1}}&{{q_2}}&{{q_3}}&{ - {q_0}}\\ {{q_0}}&{ - {q_3}}&{{q_2}}&{{q_1}}\\ {{q_3}}&{{q_0}}&{ - {q_1}}&{{q_2}}\\ { - {q_2}}&{{q_1}}&{{q_0}}&{{q_3}} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} { - 2{{\dot q}_0}}\\ {2{{\dot q}_1}}\\ {2{{\dot q}_2}}\\ {2{{\dot q}_3}} \end{array}} \right]. $

(14)

从而，角速度估计值计算式为

$ \left[ {\begin{array}{*{20}{c}} {{{\hat w}_1}}\\ {{{\hat w}_2}}\\ {{{\hat w}_3}}\\ \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {{{\hat q}_1}}&{{{\hat q}_2}}&{{{\hat q}_3}}&{ - {{\hat q}_0}}\\ {{{\hat q}_0}}&{ - {{\hat q}_3}}&{{{\hat q}_2}}&{{{\hat q}_1}}\\ {{{\hat q}_3}}&{{{\hat q}_0}}&{ - {{\hat q}_1}}&{{{\hat q}_2}}\\ { - {{\hat q}_2}}&{{{\hat q}_1}}&{{{\hat q}_0}}&{{{\hat q}_3}} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} { - 2{{\dot {\hat q}}_0}}\\ {2{{\dot {\hat q}}_1}}\\ {2{{\dot {\hat q}}_2}}\\ {2{{\dot {\hat q}}_3}} \end{array}} \right]. $

(15)

利用上式即可根据$\hat {\boldsymbol{q}} $和$\dot {\hat {\boldsymbol{q}}} $计算得出估计角速度$\hat {\boldsymbol{w}} $，其中Θ由于对q和$\dot {\boldsymbol{q}} $的估计误差而产生，是接近零值的小数，并可作为角速度估计的精度指标.

由于$\hat {\boldsymbol{q}} $和$\dot {\hat {\boldsymbol{q}}} $均收敛到真值附近，故$\hat {\boldsymbol{w}} $也收敛到真值附近，则角速度估值可表示为$\boldsymbol{w}= \hat {\boldsymbol{w}} +{\boldsymbol{o}}(\hat {\boldsymbol{w}} )$, 其中ο($\hat {\boldsymbol{w}} $)为很小的角速度估计误差.则卫星姿态动力学模型可表示为

$ \mathit{\boldsymbol{J\dot {\hat w}}} = - {{\mathit{\boldsymbol{\hat w}}}^ \times }\mathit{\boldsymbol{J\hat w}} + \mathit{\boldsymbol{u}} + \mathit{\boldsymbol{d}} + \lambda\left( {\mathit{\boldsymbol{o}}\left( {\mathit{\boldsymbol{\hat w}}} \right)} \right). $

(16)

其中λ(ο($\hat {\boldsymbol{w}} $))=-$\hat {\boldsymbol{w}} $^×Jο($\hat {\boldsymbol{w}} $)-ο($\hat {\boldsymbol{w}} $)^×Jw-Jȯ($\hat {\boldsymbol{w}} $)为角速度估计误差导致的系统综合状态误差.对应的卫星姿态跟踪动力学方程为

$ \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot {\hat w}}}}_e} = - {{\mathit{\boldsymbol{\hat w}}}^ \times }\mathit{\boldsymbol{J\hat w}} + \mathit{\boldsymbol{J}}\left( {\mathit{\boldsymbol{\hat w}}_e^ \times {{\mathit{\boldsymbol{\hat R}}}_d}{\mathit{\boldsymbol{w}}_d} - {{\mathit{\boldsymbol{\hat R}}}_d}{\mathit{\boldsymbol{w}}_d}} \right) + \mathit{\boldsymbol{u}} + \lambda\left( \mathit{\boldsymbol{o}} \right) + \mathit{\boldsymbol{d}}. $

(17)

其中$\hat {\boldsymbol{w}}_e =\hat {\boldsymbol{w}} -\hat {\boldsymbol{R}_d}$w_d, $\hat {\boldsymbol{R}_d} $为期望姿态坐标系到角速度观测系统坐标系的旋转矩阵.

假设2  假设航天器飞行控制中，角速度w与角加速度$\dot {\boldsymbol{w}} $有界.

由式(9)可知，$\ddot {\hat {\boldsymbol{q}}} $有界，同时$\dot {\hat {\boldsymbol{q}}} $有界，故根据式(15)可知$\dot {\hat {\boldsymbol{w}}} $有界，所以ȯ($\hat {\boldsymbol{w}} $)有界，最终得到系统状态综合误差λ(ο($\hat {\boldsymbol{w}} $))有界.

3 干扰观测器与控制器设计

为实现有限时间控制，采用终端滑模进行控制器设计，设计非奇异终端滑模面为

$ \mathit{\boldsymbol{s}} = {{\mathit{\boldsymbol{\hat w}}}_e} + k \cdot \beta \left( {{\mathit{\boldsymbol{q}}_{ev}}} \right). $

(18)

其中s=[s₁ s₂ s₃]^T∈R³，k>0，非奇异项β(q_ev)=[β(q_e1) β(q_e2) β(q_e3)]^T为

$ \beta \left( {{q_{ei}}} \right) = \left\{ \begin{array}{l} {\rm{si}}{{\rm{g}}^r}\left( {{q_{ei}}} \right),若\;{{\bar s}_i} = 0\;或\;{{\bar s}_i} \ne 0,\left| {{q_{ei}}} \right| > \mathit{\Phi };\\ {a_{11}}{q_{ei}} + {a_{12}}{\rm{si}}{{\rm{g}}^2}\left( {{q_{ei}}} \right),若\;{{\bar s}_i} \ne 0,\left| {{q_{ei}}} \right| \le \mathit{\Phi }\mathit{.} \end{array} \right. $

(19)

其中s_i=$\hat w _{ei}$+k·sig^r(q_ei)，i=1、2、3，0＜r＜1，sig^r(q_ei)=|q_ei|^r·sig(q_ei)，a₁₁=(2-r)Φ^r-1, a₁₂=(r-1)Φ^r-2，Φ为小的正常数.

结合式(17)，得到系统方程为

$ \begin{array}{l} {\mathit{\boldsymbol{J}}_0}\mathit{\boldsymbol{\dot s}} = {\mathit{\boldsymbol{J}}_0}{{\mathit{\boldsymbol{\dot {\hat w}}}}_e} + k \cdot {\mathit{\boldsymbol{J}}_0}\dot \beta \left( {{\mathit{\boldsymbol{q}}_{ev}}} \right) = - {{\mathit{\boldsymbol{\hat w}}}^ \times }{\mathit{\boldsymbol{J}}_0}\mathit{\boldsymbol{\hat w}} + \\ \;\;\;\;\;\;\;\;{\mathit{\boldsymbol{J}}_0}\left( {\mathit{\boldsymbol{\hat w}}_e^ \times {{\mathit{\boldsymbol{\hat R}}}_d}{\mathit{\boldsymbol{w}}_d} - {{\mathit{\boldsymbol{\hat R}}}_d}{\mathit{\boldsymbol{w}}_d}} \right) + k \cdot {\mathit{\boldsymbol{J}}_0}\dot \beta \left( {{\mathit{\boldsymbol{q}}_{ev}}} \right) + \mathit{\boldsymbol{u}} - \\ \;\;\;\;\;\;\;\;\Delta \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot {\hat w}}}}_e} - {{\mathit{\boldsymbol{\hat w}}}^ \times }\Delta \mathit{\boldsymbol{J\hat w}} + \Delta \mathit{\boldsymbol{J}}\left( {\mathit{\boldsymbol{\hat w}}_e^ \times {{\mathit{\boldsymbol{\hat R}}}_d}{\mathit{\boldsymbol{w}}_d} - {{\mathit{\boldsymbol{\hat R}}}_d}{\mathit{\boldsymbol{\dot w}}_d}} \right) + \\ \;\;\;\;\;\;\;\;\mathit{\boldsymbol{d}} + \lambda \left( {\mathit{\boldsymbol{o}}\left( {\mathit{\boldsymbol{\hat w}}} \right)} \right). \end{array} $

(20)

其中

$ \dot \beta \left( {{q_{ei}}} \right) = \left\{ \begin{array}{l} r{\left| {{q_{ei}}} \right|^{r - 1}}{{\dot q}_{ei}},若\;{{\bar s}_i} = 0\;或\;{{\bar s}_i} \ne 0,\left| {{q_{ei}}} \right| > \mathit{\Phi };\\ {a_{11}}{{\dot q}_{ei}} + 2{a_{12}}\left| {{q_{ei}}} \right|{{\dot q}_{ei}},若\;{{\bar s}_i} \ne 0,\left| {{q_{ei}}} \right| \le \mathit{\Phi }\mathit{.} \end{array} \right. $

系统的标称部分可表示为

$ \begin{array}{l} \mathit{\boldsymbol{h}}\left( t \right) = - {{\mathit{\boldsymbol{\hat w}}}^ \times }{\mathit{\boldsymbol{J}}_0}\mathit{\boldsymbol{\hat w}} + {\mathit{\boldsymbol{J}}_0}\left( {\mathit{\boldsymbol{\hat w}}_e^ \times {{\mathit{\boldsymbol{\hat R}}}_d}{\mathit{\boldsymbol{w}}_d} - {{\mathit{\boldsymbol{\hat R}}}_d}{\mathit{\boldsymbol{\dot w}}_d}} \right) + \\ \;\;\;\;\;\;\;\;\;k \cdot {\mathit{\boldsymbol{J}}_0}\dot \beta \left( {{\mathit{\boldsymbol{q}}_{ev}}} \right). \end{array} $

(21)

系统的综合不确定部分可表示为

$ \mathit{\boldsymbol{\chi }}\left( t \right) = \mathit{\boldsymbol{d}} + \lambda \left( {\mathit{\boldsymbol{o}}\left( {\mathit{\boldsymbol{\hat w}}} \right)} \right) - {{\mathit{\boldsymbol{\hat w}}}^ \times }\Delta \mathit{\boldsymbol{J\hat w}} + {\mathit{\boldsymbol{\chi }}_1}\left( t \right). $

(22)

其中:

$ \begin{array}{l} {\mathit{\boldsymbol{\chi }}_1}\left( t \right) = - \Delta \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot {\hat w}}}}_e} + \Delta \mathit{\boldsymbol{J}}\left( {\mathit{\boldsymbol{\hat w}}_e^ \times {{\mathit{\boldsymbol{\hat R}}}_d}{\mathit{\boldsymbol{w}}_d} - {{\mathit{\boldsymbol{\hat R}}}_d}{\mathit{\boldsymbol{\dot w}}_d}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\; - \Delta \mathit{\boldsymbol{J}}{\left( {\mathit{\boldsymbol{\hat w}} - {{\mathit{\boldsymbol{\hat R}}}_d}{\mathit{\boldsymbol{w}}_d}} \right)^\prime } + \Delta \mathit{\boldsymbol{J}}\left( {\mathit{\boldsymbol{\hat w}}_e^ \times {{\mathit{\boldsymbol{\hat R}}}_d}{\mathit{\boldsymbol{w}}_d} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {{{\mathit{\boldsymbol{\hat R}}}_d}{\mathit{\boldsymbol{\dot w}}_d}} \right) = - \Delta \mathit{\boldsymbol{J}}\left( {\mathit{\boldsymbol{\dot {\hat w}}} - {{\mathit{\boldsymbol{\hat R}}}_d}{{\mathit{\boldsymbol{\dot w}}}_d} + \mathit{\boldsymbol{\hat w}}_e^ \times {{\mathit{\boldsymbol{\hat R}}}_d}{\mathit{\boldsymbol{w}}_d}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\Delta \mathit{\boldsymbol{J}}\left( {\mathit{\boldsymbol{\hat w}}_e^ \times {{\mathit{\boldsymbol{\hat R}}}_d}{\mathit{\boldsymbol{w}}_d} - {{\mathit{\boldsymbol{\hat R}}}_d}{\mathit{\boldsymbol{w}}_d}} \right) = - \Delta \mathit{\boldsymbol{J\dot {\hat w}}}. \end{array} $

(23)

即综合不确定为

$ \mathit{\boldsymbol{\chi }}\left( t \right) = \mathit{\boldsymbol{d}} + \lambda \left( {\mathit{\boldsymbol{o}}\left( {\mathit{\boldsymbol{\hat w}}} \right)} \right) - {{\mathit{\boldsymbol{\hat w}}}^ \times }\Delta \mathit{\boldsymbol{J\hat w}} - \Delta \mathit{\boldsymbol{J\dot {\hat w}}}. $

(24)

故姿态跟踪系统可整理为

$ {\mathit{\boldsymbol{J}}_0}\mathit{\boldsymbol{\dot s}} = \mathit{\boldsymbol{h}}\left( t \right) + \mathit{\boldsymbol{\chi }}\left( t \right) + \mathit{\boldsymbol{u}}. $

(25)

在航天器飞行过程中，d，ΔJ，$\hat {\boldsymbol{w}} $和$\dot {\hat {\boldsymbol{w}}} $有界，同时λ(ο($\hat {\boldsymbol{w}} _i$))也有界，故综合不确定χ(t)是有界的.假设‖χ(t)‖²≤γ, 其中γ为未知正常数.针对系统(25)，设计有限时间连续自适应干扰观测器为

$ {{\mathit{\boldsymbol{\dot z}}}_d} = \mathit{\boldsymbol{h}}\left( t \right) + \mathit{\boldsymbol{\hat \chi }}\left( t \right) + \mathit{\boldsymbol{u}}, $

(26)

$ \mathit{\boldsymbol{\hat \chi }}\left( t \right) = - {\sigma _1}{\mathit{\boldsymbol{e}}_d} - {\sigma _2}{\rm{si}}{{\rm{g}}^{{r_d}}}\left( {{\mathit{\boldsymbol{e}}_d}} \right) - \frac{{\hat \gamma {\mathit{\boldsymbol{e}}_d}}}{{2\varepsilon _d^2}}. $

(27)

其中e_d=z_d-J₀s，自适应增益为

$ \dot {\hat \gamma} = {k_{d1}}\left( {\frac{{{{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|}^2}}}{{2\varepsilon _d^2}} - {k_{d2}}\hat \gamma } \right). $

(28)

参数σ₁>0, σ₂>0，k_d1>0, k_d2>0，ε_d>0，指数0＜r_d＜1.

定理1  针对非线性系统(25)，设计自适应干扰观测器(26)~(28)，则干扰估计值$\hat {\boldsymbol{\chi}} \left( t \right) $在有限时间内收敛到χ(t)附近邻域内.

证明  选取Lyapunov候选函数为

$ {V_1} = \frac{1}{2}\mathit{\boldsymbol{e}}_d^{\rm{T}}{\mathit{\boldsymbol{e}}_d} + \frac{1}{{2{k_{d1}}}}{{\tilde \gamma }^2}. $

(29)

其中$ \tilde \gamma = \hat \gamma - \gamma $. V₁对时间求导，得到

$ \begin{array}{l} {{\dot V}_1} = \mathit{\boldsymbol{e}}_d^{\rm{T}}{{\mathit{\boldsymbol{\dot e}}}_d} + \frac{1}{{{k_{d1}}}}\tilde \gamma \dot {\hat \gamma} = \\ \mathit{\boldsymbol{e}}_d^{\rm{T}}\left( { - {\sigma _1}{\mathit{\boldsymbol{e}}_d} - {\sigma _2}{\rm{si}}{{\rm{g}}^{{r_d}}}\left( {{\mathit{\boldsymbol{e}}_d}} \right) - \frac{{\hat \gamma {\mathit{\boldsymbol{e}}_d}}}{{2\varepsilon _d^2}} - \mathit{\boldsymbol{\chi }}\left( t \right)} \right) + \\ \tilde \gamma \left( {\frac{{{{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|}^2}}}{{2\varepsilon _d^2}} - {k_{d2}}\hat \gamma } \right) \le - {\sigma _1}{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|^2} - \\ {\sigma _2}\sum\limits_{j = 1}^3 {{{\left| {{\mathit{\boldsymbol{e}}_{dj}}} \right|}^{{r_d} + 1}}} - \frac{{\gamma {{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|}^2}}}{{2\varepsilon _d^2}} - \mathit{\boldsymbol{e}}_d^{\rm{T}}\mathit{\boldsymbol{\chi }}\left( t \right) - {k_{d2}}\hat \gamma \tilde \gamma \le \\ - {\sigma _1}{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|^2} - \frac{{\gamma {{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|}^2}}}{{2\varepsilon _d^2}} + \left\| {{\mathit{\boldsymbol{e}}_d}} \right\|\left\| {\mathit{\boldsymbol{\chi }}\left( t \right)} \right\| - {k_{d2}}\hat \gamma \tilde \gamma . \end{array} $

考虑到$ \frac{{\gamma {{\left\| {{\boldsymbol{e}_d}} \right\|}^2}}}{{2\varepsilon _d^2}} + \frac{{\varepsilon _d^2}}{2} \ge \left\| {{\boldsymbol{e}_d}} \right\|\sqrt \gamma $，故可得到

$ \begin{array}{l} {{\dot V}_1} \le - {\sigma _1}{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|^2} - {k_{d2}}\hat \gamma \tilde \gamma + \frac{{\varepsilon _d^2}}{2} \le \\ \;\;\;\; - {\sigma _1}{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|^2} - {k_{d2}}{{\tilde \gamma }^2} - {k_{d2}}\gamma \tilde \gamma + \frac{{\varepsilon _d^2}}{2}. \end{array} $

(30)

由于$ - \gamma \tilde \gamma \le \frac{1}{2}{\gamma ^2} + \frac{1}{2}{{\tilde \gamma }^2}$，则上式可得

$ \begin{array}{l} {{\dot V}_1} \le - {\sigma _1}{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|^2} + \frac{{{k_{d2}}}}{2}{\gamma ^2} - \frac{{{k_{d2}}}}{2}{{\tilde \gamma }^2} + \frac{{\varepsilon _d^2}}{2} \le \\ \; - \frac{{2{\sigma _1}}}{2}{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|^2} - \frac{{{k_{d1}}{k_{d2}}}}{{2{k_{d1}}}}{{\tilde \gamma }^2} + \frac{{{k_{d2}}}}{2}{\gamma ^2} + \frac{{\varepsilon _d^2}}{2} \le \\ \;\;\;\;\;\; - \tilde \alpha {V_1} + \frac{{{k_{d2}}}}{2}{\gamma ^2} + \frac{{\varepsilon _d^2}}{2}. \end{array} $

(31)

其中$ \overline \alpha$=min{2σ₁, k_d1k_d2}，根据有界性定理，可知e_d和$\tilde \gamma $一致最终有界(UUB).所以存在一个正常数$ \overline \gamma$，使得$\left| {\tilde \gamma } \right| \le \overline \gamma $成立.基于此，定义一个新Lyapunov函数

$ {{\bar V}_1} = \frac{1}{2}\mathit{\boldsymbol{e}}_d^{\rm{T}}{\mathit{\boldsymbol{e}}_d}. $

(32)

其时间导数为

$ \begin{array}{l} {{\dot {\bar V}}_1} = \mathit{\boldsymbol{e}}_d^{\rm{T}}\left( { - {\sigma _1}{\mathit{\boldsymbol{e}}_d} - {\sigma _2}{\rm{si}}{{\rm{g}}^{{r_d}}}\left( {{\mathit{\boldsymbol{e}}_d}} \right) - \frac{{\hat \gamma {\mathit{\boldsymbol{e}}_d}}}{{2\varepsilon _d^2}} - \mathit{\boldsymbol{\chi }}\left( t \right)} \right) \le \\ \;\;\; - {\sigma _1}{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|^2} - {\sigma _2}\sum\limits_{j = 1}^3 {{{\left| {{\mathit{\boldsymbol{e}}_{dj}}} \right|}^{1 + {r_d}}} - \frac{{\hat \gamma {{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|}^2}}}{{2\varepsilon _d^2}} + } \\ \;\;\;\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|\left\| {\mathit{\boldsymbol{\chi }}\left( t \right)} \right\| \le {\sigma _1}{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|^2} - {\sigma _2}{\left( {{{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|}^2}} \right)^{\frac{{1 + {r_d}}}{2}}} - \\ \;\;\;\frac{{\tilde \gamma {{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|}^2}}}{{2\varepsilon _d^2}} + \frac{{\varepsilon _d^2}}{2}. \end{array} $

(33)

所以，可得到

$ \begin{array}{l} {{\dot {\bar V}}_1} \le - {\sigma _1}{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|^2} - {\sigma _2}{\left( {{{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|}^2}} \right)^{\frac{{1 + {r_d}}}{2}}} + \\ \;\;\;\;\;\;\frac{{|\tilde \gamma| {{\left\| {{\mathit{\boldsymbol{e}}_d}} \right\|}^2}}}{{2\varepsilon _d^2}} + \frac{{\varepsilon _d^2}}{2} \le - 2\left( {{\sigma _1} - \underline {2\varepsilon _d^2} } \right){{\bar V}_1} - \\ \;\;\;\;\;\;{\sigma _2}\left( {{2^{\frac{{1 + {r_d}}}{2}}} - \frac{{\varepsilon _d^2}}{{2\bar V_1^{\frac{{1 + {r_d}}}{2}}}}} \right)\bar V_1^{\frac{{1 + {r_d}}}{2}}. \end{array} $

(34)

由上式可得，若选择σ₁≥ $ \overline \gamma$/(2ε_d²)，则V₁会在有限时间T内收敛到V₁≤ $\frac{1}{2}{\left( {\varepsilon _d^2/2} \right)^{2/\left( {1 + {r_d}} \right)}} $, 故当t>T时观测误差满足|e_dj|≤ ${\left( {\varepsilon ^2/2} \right)^{1/\left( {1 + {r_d}} \right)}} $, (j=1, 2, 3).观测误差导数满足$\int_T^\infty {{{\dot {\boldsymbol{e}}}_d}} {\rm{d}}t $=e_d(∞)-e_d(T), 故当t>T时，-2(ε²/2)^1/(1+r_d)≤ $ \int_T^\infty {{{\dot {\boldsymbol{e}}}_{dj}}} {\rm{d}}t$≤2(ε²/2)^1/(1+r_d), 可得${{{\dot e}_d}} $有界，即$\left\| {\hat {\boldsymbol{\chi}} \left( t \right) - {\boldsymbol{\chi}} \left( t \right)} \right\| $有界.易得$\left\| {{{\dot {\boldsymbol{e}}}_d}} \right\| \le {\sigma _1}\left\| {{{\boldsymbol{e}}_d}} \right\| + {\sigma _2}\left\| {{\rm{si}}{{\rm{g}}^{{r_d}}}\left( {{{\boldsymbol{e}}_d}} \right)} \right\| + \frac{{\hat \gamma \left\| {{{\boldsymbol{e}}_d}} \right\|}}{{2\varepsilon _d^2}} + \sqrt \gamma $, 干扰观测误差在有限时间内收敛阈值为$\left\| {{{\dot {\boldsymbol{e}}}_d}} \right\| \le \sqrt 3 \left( {{\sigma _1} + {\sigma _2}{{\left( {\frac{{{\varepsilon ^2}}}{2}} \right)}^r} + \frac{{2\varepsilon _d^2}}{{}}} \right){\left( {\frac{{{\varepsilon ^2}}}{2}} \right)^{\frac{1}{{1 + {r_d}}}}} + \sqrt \gamma $，假设观测误差上界为ψ，得到$\hat {\boldsymbol{\chi}} \left( t \right) $最终收敛至χ(t)邻域内.证毕.

注3  相比于之前的刚体航天器自适应滑模控制器^[16-18]，设计的干扰观测器(27)自适应项中避免了符号函数的引入，从而使得干扰观测值$\hat {\boldsymbol{\chi}} \left( t \right) $为连续变化值，能有效地减小观测抖振的产生，从而较好地降低控制输入抖振，改善控制性能.

由于干扰观测器(27)只能收敛到干扰真值邻域内，为抵消干扰观测器误差，提高控制精度，设计如下有限时间姿态跟踪控制器

$ \mathit{\boldsymbol{u}} = - {\zeta _1}\mathit{\boldsymbol{s}} - {\zeta _2}{\rm{si}}{{\rm{g}}^{{r_c}}}\left( \mathit{\boldsymbol{s}} \right) - \mathit{\boldsymbol{h}}\left( t \right) - \mathit{\boldsymbol{\hat \chi }}\left( t \right) - \frac{{\hat \psi \mathit{\boldsymbol{s}}}}{{\left\| \mathit{\boldsymbol{s}} \right\|}}. $

(35)

其中ζ₁>0，ζ₂>0，0＜r_c＜1. ${\hat \psi } $是对干扰观测误差上界的估计，满足$ \dot {\hat \psi } = {\lambda _\psi }\left( { - {\varepsilon _\psi }\hat \psi + \left\| \boldsymbol{s} \right\|} \right)$，参数ε_ψ>0，δ_ψ0>0.5，λ_ψ在式(39)之后给出.

推论1  考虑系统(25)和干扰观测器(27)、(28)，设计的控制器(35)在有限时间内保证q和w分别收敛至q_d和w_d附近邻域内.

证明  选取Lyapunov函数为

$ {V_2} = \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{J}}_0}s + \frac{1}{{2{\lambda _\psi }}}{{\tilde \psi }^2}. $

(36)

其中λ_min‖s‖²≤s^TJ₀s≤λ_max‖s‖²，λ_min, λ_max为正常数，$ \tilde \psi = \psi - \hat \psi $，对上式求导可得

$ \begin{array}{l} {{\dot V}_2} = {\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{J}}_0}\mathit{\boldsymbol{\dot s + }}\frac{1}{{{\lambda _\psi }}}\tilde \psi \dot {\tilde \psi} = \\ \;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}\left[ {h\left( t \right) + \chi \left( t \right) + u} \right] - \frac{1}{{{\lambda _\psi }}}\tilde \psi \dot {\tilde \psi} = \\ \;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}\left[ { - {\zeta _1}\mathit{\boldsymbol{s}} - {\zeta _2}{\rm{si}}{{\rm{g}}^{{r_c}}}\left( \mathit{\boldsymbol{s}} \right) + \mathit{\boldsymbol{\chi }}\left( t \right) - \mathit{\boldsymbol{\hat \chi }}\left( t \right) - \frac{{\hat \psi \mathit{\boldsymbol{s}}}}{{\left\| \mathit{\boldsymbol{s}} \right\|}}} \right] - \\ \;\;\;\frac{1}{{{\lambda _\psi }}}\tilde \psi \dot {\hat \psi} \le - {\zeta _2}\sum\limits_{i = 1}^3 {{{\left| {{s_i}} \right|}^{1 + {r_c}}} + \left\| s \right\|\psi - \left\| s \right\|\hat \psi - } \\ \;\;\;\tilde \psi \left( { - {\varepsilon _\psi }\hat \psi + \left\| \mathit{\boldsymbol{s}} \right\|} \right) \le - {\zeta _2}{\left( {\sum\limits_{i = 1}^3 {s_i^2} } \right)^{\left( {1 + {r_c}} \right)/2}} + {\varepsilon _\psi }\tilde \psi \hat \psi \le \\ \;\;\; - {\zeta _2}{\left( {\frac{2}{{{\lambda _{\max }}}}} \right)^{\left( {1 + {r_c}} \right)/2}}{\left( {\frac{1}{2}{\mathit{\boldsymbol{s}}^T}{\mathit{\boldsymbol{J}}_0}\mathit{\boldsymbol{s}}} \right)^{\left( {1 + {r_c}} \right)/2}} + {\varepsilon _\psi }\tilde \psi \hat \psi . \end{array} $

(37)

其中第4到第5步可由文献[17]引理3.1推出，对于任意δ_ψ0>0.5，可推导如下

$ \begin{array}{l} {\varepsilon _\psi }\tilde \psi \hat \psi = {\varepsilon _\psi }\left( {\tilde \psi \psi - {{\tilde \psi }^2}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;{\varepsilon _\psi }\left( { - {{\tilde \psi }^2} + \frac{1}{{2{\delta _{\psi 0}}}}{{\tilde \psi }^2} + \frac{{{\delta _{\psi 0}}}}{2}{\psi ^2}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\varepsilon _\psi }{\delta _{\psi 0}}}}{2}{\psi ^2} - \frac{{{\varepsilon _\psi }\left( {2{\delta _{\psi 0}} - 1} \right)}}{{2{\delta _{\psi 0}}}}{{\tilde \psi }^2}. \end{array} $

(38)

则式(37)可整理为

$ \begin{array}{l} {{\dot V}_2} \le - {\zeta _2}{\left( {\frac{2}{{{\lambda _{\max }}}}} \right)^{\left( {1 + {r_c}} \right)/2}}{\left( {\frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm T}}{\mathit{\boldsymbol{J}}_0}\mathit{\boldsymbol{s}}} \right)^{\left( {1 + {r_c}} \right)/2}} - \\ \;\;\;\;\;\;\;{\left( {\frac{{{\varepsilon _\psi }\left( {2{\delta _{\psi 0}} - 1} \right)}}{{2{\delta _{\psi 0}}}}{{\tilde \psi }^2}} \right)^{\left( {1 + {r_c}} \right)/2}} + \\ \;\;\;\;\;\;\;{\left( {\frac{{{\varepsilon _\psi }\left( {2{\delta _{\psi 0}} - 1} \right)}}{{2{\delta _{\psi 0}}}}{{\tilde \psi }^2}} \right)^{\left( {1 + {r_c}} \right)/2}} + {\varepsilon _\psi }\tilde \psi \hat \psi \le \\ \;\;\;\;\;\;\; - {\zeta _2}{\left( {\frac{2}{{{\lambda _{\max }}}}} \right)^{\left( {1 + {r_c}} \right)/2}}\left[ {{{\left( {\frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm T}}{\mathit{\boldsymbol{J}}_0}\mathit{\boldsymbol{s}}} \right)}^{\left( {1 + {r_c}} \right)/2}} + } \right.\\ \;\;\;\;\;\;\;\left. {{{\left( {\frac{1}{{2{\lambda _\psi }}}{{\tilde \psi }^2}} \right)}^{\left( {1 + {r_c}} \right)/2}}} \right] + {\left( {\frac{{{\varepsilon _\psi }\left( {2{\delta _{\psi 0}} - 1} \right)}}{{2{\delta _{\psi 0}}}}{{\tilde \psi }^2}} \right)^{\left( {1 + {r_c}} \right)/2}} + \\ \;\;\;\;\;\;\;{\varepsilon _\psi }\tilde \psi \hat \psi . \end{array} $

(39)

其中$ {\lambda _\psi } = \frac{{2{\delta _{\psi 0}}\zeta _2^{2/{r_c} + 1}}}{{{\lambda _{\max }}{\varepsilon _\psi }\left( {2{\delta _{\psi 0}} - 1} \right)}}$，由于δ_ψ0>0.5，ε_ψ>0，由文献[17]引理3.1可得

$ \begin{array}{l} {{\dot V}_2} \le - {\zeta _2}{\left( {\frac{2}{{{\lambda _{\max }}}}} \right)^{\left( {1 + {r_c}} \right)/2}}V_2^{\left( {1 + {r_c}} \right)/2} + \\ \;\;\;\;\;\;{\left( {\frac{{{\varepsilon _\psi }\left( {2{\delta _{\psi 0}} - 1} \right)}}{{2{\delta _{\psi 0}}}}{{\tilde \psi }^2}} \right)^{\left( {1 + {r_c}} \right)/2}} + {\varepsilon _\psi }\tilde \psi \hat \psi . \end{array} $

(40)

由于0＜r_c＜1，若$\frac{{{\varepsilon _\psi }\left( {2{\delta _{\psi 0}} - 1} \right)}}{{2{\delta _{\psi 0}}}}{{\tilde \psi }^2} \ge 1 $，得到

$ \begin{array}{l} {\left( {\frac{{{\varepsilon _\psi }\left( {2{\delta _{\psi 0}} - 1} \right)}}{{2{\delta _{\psi 0}}}}{{\tilde \psi }^2}} \right)^{\left( {1 + {r_c}} \right)/2}} + {\varepsilon _\psi }\tilde \psi \hat \psi \le \\ \;\;\;\left( {\frac{{{\varepsilon _\psi }\left( {2{\delta _{\psi 0}} - 1} \right)}}{{2{\delta _{\psi 0}}}}{{\tilde \psi }^2}} \right) + {\varepsilon _\psi }\tilde \psi \hat \psi \le \frac{{{\varepsilon _\psi }{\delta _{\psi 0}}}}{2}{\psi ^2}. \end{array} $

(41)

若$ \frac{{{\varepsilon _\psi }\left( {2{\delta _{\psi 0}} - 1} \right)}}{{2{\delta _{\psi 0}}}}{\tilde \psi ^2} < 1$，则可以得到

$ \begin{array}{l} {\left( {\frac{{{\varepsilon _\psi }\left( {2{\delta _{\psi 0}} - 1} \right)}}{{2{\delta _{\psi 0}}}}{{\tilde \psi }^2}} \right)^{\left( {1 + {r_c}} \right)/2}}\left| {_{\frac{{{\varepsilon _\psi }\left( {2{\delta _{\psi 0}} - 1} \right)}}{{2{\delta _{\psi 0}}}}{{\tilde \psi }^2} < 1}} \right. < \\ \;\;\;\;\;{\left( {\frac{{{\varepsilon _\psi }\left( {2{\delta _{\psi 0}} - 1} \right)}}{{2{\delta _{\psi 0}}}}{{\tilde \psi }^2}} \right)^{\left( {1 + {r_c}} \right)/2}}\left| {_{\frac{{{\varepsilon _\psi }\left( {2{\delta _{\psi 0}} - 1} \right)}}{{2{\delta _{\psi 0}}}}{{\tilde \psi }^2} \ge 1}} \right.. \end{array} $

(42)

故总有

$ {\left( {\frac{{{\varepsilon _\psi }\left( {2{\delta _{\psi 0}} - 1} \right)}}{{2{\delta _{\psi 0}}}}{{\tilde \psi }^2}} \right)^{\left( {1 + {r_c}} \right)/2}} + {\varepsilon _\psi }\tilde \psi \hat \psi \le \frac{{{\varepsilon _\psi }{\delta_{\psi 0}}}}{2}{\psi ^2}. $

(43)

则可得

$ {{\dot V}_2} \le - {\zeta _2}{\left( {\frac{2}{{{\lambda _{\max }}}}} \right)^{\left( {1 + {r_c}} \right)/2}}V_2^{\left( {1 + {r_c}} \right)/2} + \tilde \omega . $

(44)

其中$ \tilde \omega = \frac{{{\varepsilon _\psi }{\delta _{\psi 0}}}}{2}{\psi ^2}$.上式可整理为

$ {{\dot V}_2} \le - \left[ {{\zeta _2}{{\left( {\frac{2}{{{\lambda _{\max }}}}} \right)}^{\left( {1 + {r_c}} \right)/2}} - \frac{{\bar \omega }}{{V_2^{\left( {1 + {r_c}} \right)/2}}}} \right]V_2^{\left( {1 + {r_c}} \right)/2}. $

(45)

当$ {\zeta _2}{\left( {\frac{2}{{{\lambda _{\max }}}}} \right)^{\left( {1 + {r_c}} \right)/2}} - \frac{{\tilde \omega }}{{V_2^{\left( {1 + {r_c}} \right)/2}}} > 0$时，V₂能够实现有限时间收敛，求得到V₂的有限时间收敛域为

$ {V_2} \le \frac{{{\lambda _{\max }}}}{2}{\left( {\frac{{\tilde \omega }}{{{\zeta _2}}}} \right)^{2/\left( {1 + {r_c}} \right)}}. $

(46)

故计算得出滑模面的有限时间收敛域为

$ \left\| \mathit{\boldsymbol{s}} \right\| \le \sqrt {\frac{{{\lambda _{\max }}}}{{2{\lambda _{\min }}}}} {\left( {\frac{{\bar \omega }}{{{\zeta _2}}}} \right)^{1/\left( {1 + {r_c}} \right)}}. $

(47)

依据文献[17]定理3可知，q和w在有限时间内分别收敛至q_d和w_d邻域内.证毕.

4 仿真分析

为验证所提方法的有效性，进行仿真验证与分析.仿真中，各参数选取如下

$ J = \left[ {\begin{array}{*{20}{c}} {20}&2&{0.9}\\ 2&{17}&{0.5}\\ {0.9}&{0.5}&{15} \end{array}} \right]{\rm{kg}} \cdot {{\rm{m}}^2}. $

其中标称部分J₀=diag(20 20 20) kg·m².给定外界干扰，所给干扰远比空间中环境干扰大. d_x=0.01sin(0.4t), d_y=0.005cos(0.5t), d_z=0.008cos(0.7t).

航天器姿态及角速度初值为

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{q}}\left( 0 \right) = \left[ {\begin{array}{*{20}{c}} {0.8986}&{0.4}&{ - 0.1}&{0.15} \end{array}} \right],}\\ {\mathit{\boldsymbol{w}}\left( 0 \right) = {{\left[ {\begin{array}{*{20}{c}} {0.1}&{0.05}&{ - 0.1} \end{array}} \right]}^{\rm{T}}}.} \end{array} $

期望姿态与角速度为

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{q}}_d}\left( 0 \right) = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \end{array}} \right],}\\ {\mathit{\boldsymbol{w}}\left( t \right) = 0.1{{\left[ {\cos \left( {t/40} \right) - \sin \left( {t/50} \right) - \cos \left( {t/60} \right)} \right]}^{\rm{T}}}.} \end{array} $

状态观测器参数设计为k₁=0.1，k₂=0.01，$\overline \varepsilon $=0.01，φ=0.02，$\hat {\boldsymbol{q}} $(0)=[0.7  0.1  0.2  0.3]，v(0)=[0  0  0  0]，α₁(0)=0.3.

干扰观测器参数设计为σ₁=2，σ₂=0.5，k_d1=0.1，k_d2=20，ε_d=0.5，指数r_d=0.7，z_d(0)=[0  0  0]，γ(0)=1.

控制器参数设计为ζ₁=ζ₂=1，r_c=0.7，ε_ψ=0.2，δ_a0=1，λ_max=20，$\hat \gamma_a $(0)=0，控制约束为u_max=-u_min=0.5 N·m.

为更好说明角速度估计算法优越性，将其与滤波器估计算法进行比较，滤波器算法^[8]为

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot q}} = - a\mathit{\boldsymbol{q}} + \mathit{\boldsymbol{p}},\\ \mathit{\boldsymbol{\dot p}} = - \left( {a + 1} \right)\mathit{\boldsymbol{p}} + \left( {{a^2} + 1} \right)\mathit{\boldsymbol{q}}. \end{array} \right. $

(48)

其中a>0为滤波器增益，p为滤波器辅助变量，满足p(0)=aq，采用试凑法仿真中取a=22.

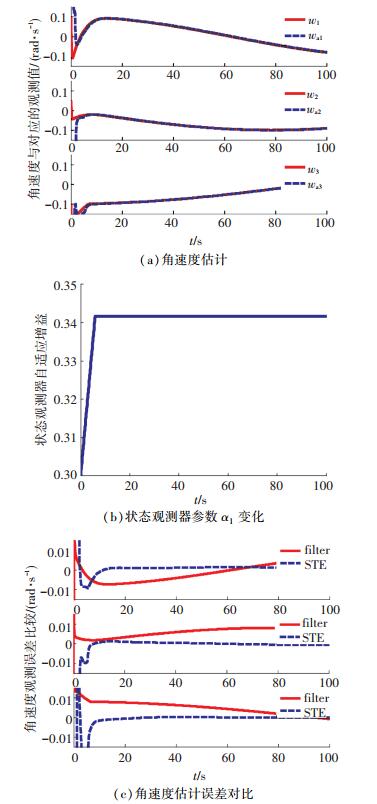
图 1所示为基于观测器(9)的角速度估计效果以及与基于滤波器(48)的角速度估计对比，其中标注w为真实角速度，标注w_a为对应观测值.可以看出设计的角速度观测算法能在数秒内实现对真实角速度的较高精度估计，并且估值中没有抖振；由于设定了观测精度阈值，状态观测器增益也不会发生过估计问题；同时设计的角速度估计算法精度相比基于滤波器的角速度估计精度有明显提高，说明了所设计的角速度估计算法的优越性.

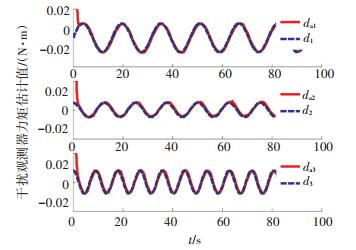
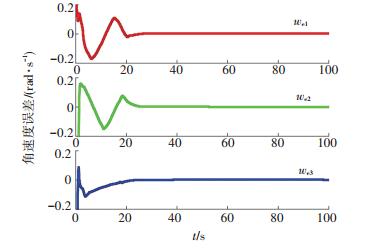
图 2为自适应干扰观测器对设定外界干扰的估计，标注d为真实干扰，d_a为对应观测值.虽然式(27)只能保证干扰观测误差收敛到一定范围内，但在应用中容易看出干扰观测器能很快实现对给定干扰的较高精度估计，并且干扰观测值是连续无抖振. 图 3、4为控制过程中，四元数误差和角速度误差的变化曲线，可以看出航天器的姿态误差和角速度误差值在有限时间内收敛到平衡点附近. 图 5为对应的控制输入曲线，可以看出控制输入在设计的约束范围内，同时控制输入信号无抖振.

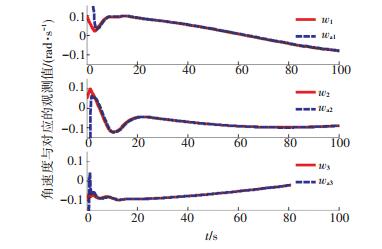
为进一步说明所设计观测器和控制器的有效性，将所提方法与纯自适应滑模控制进行对比，设计纯自适应滑模姿态控制器为^[17]

$ \mathit{\boldsymbol{u}} = - {\zeta _1}\mathit{\boldsymbol{s}} - {\zeta _2}si{g^{{r_c}}}\left( \boldsymbol{s} \right) - \mathit{\boldsymbol{h}}\left( t \right) - {{\hat \gamma }_a}\mathit{\boldsymbol{s}}/\left\| \mathit{\boldsymbol{s}} \right\|. $

其中$ \hat \gamma_a$为χ(t)的上界，并且${{\dot {\hat \gamma} }_a} = {\lambda _a}\left( { - {\varepsilon _a}{{\hat \gamma }_a} + \left\| \boldsymbol{s} \right\|} \right) $，其参数满足ε_a>0，λ_a= $ \frac{{2{\delta _{a0}}\sigma _2^{2/r + 1}}}{{{\lambda _{\max }}{\varepsilon _a}\left( {2{\delta _{a0}} - 1} \right)}}$，δ_a0>0.5.在仿真中取ε_a=0.1，δ_a0=1，λ_max=20，$\hat \gamma_a (0) $=0.对应的仿真结果如图 6、7所示.

可以看出，设计的角速度观测器能够实现对角速度的高精度估计，同时对比图 5、7，容易得出本文设计的控制器能够较好地减小控制器的抖振，说明了所设计干扰观测器和控制器的优越性.

5 结论

1) 研究了角速度不可测的刚体航天器有限时间姿态跟踪控制.分别设计了基于超螺旋滑模状态观测器的角速度估计算法和有限时间自适应干扰观测器.

2) 设计的角速度估计算法比传统滤波估计算法具有更高的精度，同时干扰观测器结合了连续自适应技术，实现了干扰的连续估计，并减小了控制输入抖振.

3) 仿真结果验证了所提算法的有效性，对工程应用有一定参考意义.但只研究了刚体航天器的姿态跟踪控制，对于挠性航天器以及故障条件下的航天器姿态控制有待进一步研究.