2. 中国航天科技九院第16研究所,西安 710100;
3. 中国航天科技五院第504研究所,西安 710100
2. The 16th Institute, China Aerospace Times Electronics Corporation, Xi'an 710100, China;
3. The 504th Institute, China Aerospace Science and Technology Corporation, Xi'an 710100, China
半球型动压气体轴承永磁陀螺电机作为高精度三浮陀螺的心脏,主要为陀螺提供动量矩.电机工作时,转动部分和静止部分被气膜隔离,没有接触磨擦,是研制高精度、长寿命陀螺仪表的理想元件.
美国德雷珀实验室第四代陀螺仪表(fourth generation gyroscope,简称“FGG”)采用的就是半球型动压气体轴承永磁陀螺电机,成功应用于其MX导弹浮球平台系统中[1].英国Smith公司700系列和2000系列陀螺文献报导,柱型动压气体轴承磁滞同步电机采用热化学法实施碳化硼表面改性技术,可显著提高轴承表面质量,减少摩擦系数,使陀螺电机启停次数从10 000次提高到了100 000次[2].
国内从上世纪70年代开始柱型动压气体轴承技术攻关,主要采用柱型动压气体轴承磁滞同步电机.进入90年代以来,随着气体轴承技术的进步,柱型动压气体轴承陀螺电机启停寿命得到明显提高,电机启停次数可超过3 000次,实现工程应用[3-5].近几年开始研制半球型动压气体轴承永磁陀螺电机样机,先后突破了半球轴承零件的超精密机械加工[6-9]、轴承零件表面改性[10-11]、轴承刚度测试[12]等方面的技术,但仍然存在不少动压气体轴承的瓶颈问题亟待研究和突破,其中动压气体轴承的启停寿命是最为突出的一个关键问题.根据星用高精度三浮陀螺应用要求,陀螺电机启停次数须不少于3 000次.
动压气体轴承陀螺电机启停寿命及可靠性问题涉及方面很多,从轴承材料选择、螺旋槽以及轴承间隙参数设计、轴承零件加工、部件组合、装配与试验到装至陀螺中,每一步骤、每一环节都得细致准确进行[13-16].
本文将针对陀螺电机用半球型动压气体轴承的设计理论以及保证轴承在电机工况下能可靠启停的关键技术进行分析研究,在此基础上研制了半球型动压气体轴承陀螺电机(以下简称“半球动压电机”)样机,并进行专项的电机启停寿命试验.
1 半球动压电机的基本结构半球型动压气体轴承永磁陀螺电机主要包括电机定子、转子、动压气体轴承以及永磁无刷电机控制器4个部分.其中动压气体轴承是陀螺电机的关键技术.半球型动压气体轴承与柱型结构相比,其姿态角小,电机垂直启动性能较好.因此对于高精度三浮陀螺仪表最好选用半球型动压气体轴承.
半球动压电机本体结构如图 1所示.其中左半球、右半球、转子盖是半球型动压气体轴承的关键零件,结构图分别如图 2、3所示.

|
图 1 半球动压电机结构示意图 Figure 1 Structure of hemispheric aerodynamic bearing motor |

|
图 2 左(右)半球的结构图 Figure 2 Left(right) hemisphere |

|
图 3 转子盖结构图 Figure 3 Rotor cover |
动压气体轴承设计是半球动压电机的关键技术.
2.1 动压气体轴承材料选择动压气体轴承材料的性能关系到轴承能否正常工作,进而决定轴承的寿命.本文研制的半球型动压气体轴承选用GT-35钢结硬质合金材料.
GT-35是以碳化钛为硬质相,铁粉、铬、钼等元素为钢基体粘结剂的一种硬质合金.它具有一般合金工具钢的可加工、可热处理、可锻造、可焊接的性能,又具有硬质合金的高硬度(淬火后)、高耐磨等特点,精加工表面光洁度可达到▽13以上.但是这种材料表面孔隙率不够稳定,常有麻点及疏松孔,也不耐腐蚀.因此在实际应用时与其他材料相比验收要求更严格一些,尤其是孔隙度和淬火硬度.
2.2 动压气体轴承的基本方程基于球面螺旋槽近似理论、惠普尔平行槽对称压力分布理论,动压润滑在膜内的流动过程接近于等温过程,为简化计算,假定气体为等温、等粘度理想气体,气体润滑表面是不变形的刚体表面.轴承间隙内的气体流动可由如下非定常可压缩Reynolds方程描述为
| $ \frac{\partial }{{\partial x}}\left( {p{h^3}\frac{{\partial p}}{{\partial x}}} \right) + \frac{\partial }{{\partial z}}\left( {p{h^3}\frac{{\partial p}}{{\partial z}}} \right) = 6\mu \omega \frac{{\partial \left( {ph} \right)}}{{\partial x}} + 12\mu \frac{{\partial \left( {ph} \right)}}{{\partial t}}. $ | (1) |
式中:p为气膜压力,Pa;h为轴承间隙,m;ω为转子转速,rad/s;μ为气体粘度,Pa·s;t为时间,s;x、z为坐标.
式(1)等式左边是气膜压力沿x、z方向的分布,是二维关系式;等式右边第1项为运动润滑表面旋转的速度,第2项为气体支承的两润滑表面在气膜法向上的相对速度所引起的挤压膜作用.
对气体轴承的稳态条件下性能进行分析,因此对式(1)的求解将舍去非定常项(时间项),得到定常可压缩Reynolds方程为
| $ \frac{\partial }{{\partial x}}\left( {p{h^3}\frac{{\partial p}}{{\partial x}}} \right) + \frac{\partial }{{\partial z}}\left( {p{h^3}\frac{{\partial p}}{{\partial z}}} \right) = 6\mu \omega \frac{{\partial \left( {ph} \right)}}{{\partial x}}. $ | (2) |
引入无量纲量:
| $ P=p/P_a,\;H=h/h_0,\;X=x/l,\;Z=z/l. $ |
其中Pa、h0、l为无量纲式所取的参考量.
将上面无量纲量代入式(2),则得到轴承的无量纲Reynolds方程为
| $ \frac{\partial }{{\partial X}}\left( {P{H^3}\frac{{\partial P}}{{\partial X}}} \right) + \frac{\partial }{{\partial Z}}\left( {P{H^3}\frac{{\partial P}}{{\partial Z}}} \right) = \Lambda \frac{{\partial \left( {PH} \right)}}{{\partial X}}, $ | (3) |
式中:∧为压缩数或轴承数,是判断轴承压缩效应及切向速度影响的特性数,∧=6 μωl/Pah02.
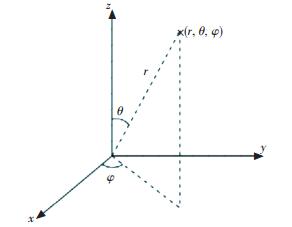
半球型动压气体轴承表面具有球面或者球冠结构,因此在计算过程中,采用球坐标系求解Reynolds方程是较好的选择.球坐标系如图 4所示,采用(r、θ、φ)表示空间中一点的坐标,坐标转换关系式为x=rsin θcos φ, y=rsin θsin φ, z=rcos θ, 那么球坐标系中对置式半球型气体轴承内的定常可压缩Reynolds方程为
|
图 4 球面坐标系示意图 Figure 4 Spherical coordinate system |
| $ \frac{\partial }{{\partial \varphi }}\left( {p{h^3}\frac{{\partial p}}{{\partial \varphi }}} \right) + \sin \theta \frac{\partial }{{\partial \theta }}\left( {\sin \theta p{h^3}\frac{{\partial p}}{{\partial \theta }}} \right) = 6\mu \omega {r^2}\sin^2 \theta \frac{{\partial \left( {ph} \right)}}{{\partial \varphi }}. $ | (4) |
可见轴承内气膜的Reynolds方程为一非线性二阶偏微分方程,建立半球型动压轴承的有限元分析模型,将影响轴承性能的主要参数作为变量,通过改变变量参数来分析半球轴承力学指标的变化趋势.分析认为在轴承半径确定前提下,轴承机械间隙和螺旋槽结构参数是影响轴承力学性能的关键因素[14].轴承间隙一般要求尽可能小,以保证轴承刚度最大,但又受制于精密机械加工精度和陀螺电机特殊工况下轴承各种微变形的限制,所以动压气体轴承机械间隙2 μm是否合理,这需要重点分析.
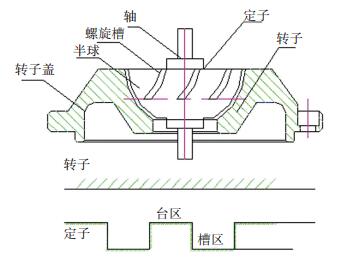
2.3 动压气体轴承螺旋槽设计半球型动压气体轴承采用球面螺旋槽,其主要由轴承转子和定子两部分组成,转子凸半球零件表面上开有一定数量的螺旋槽,螺旋槽由槽区和台区组成,如图 5所示.
|
图 5 半球动压气体轴承剖面示意图 Figure 5 Sections of hemispheric aerodynamic bearing |
螺旋槽型的基本结构如图 6所示.一般开泵进型螺旋槽,使气流由与环境相通的一端向轴承间隙内流动,气流在轴承面光滑处被节流,构成压力升高,半球型动压气体轴承的刚度决定着轴承的抗力学环境能力和转子的回转精度,进而影响了电机转子动量矩的稳定性.半球动压气体轴承的刚度与轴承表面螺旋槽结构参数有很大关系.

|
图 6 半球螺旋槽型结构图 Figure 6 Structure of the spiral groove |
半球型动压轴承陀螺电机的球面螺旋槽参数仿真分析时,分别将图 6中螺旋槽倾角ψGD、半球小端止角、螺旋槽小端止角ψGC、螺旋槽深、螺旋槽槽台比值(槽区和台区宽度之比Ag/Ar)作为参变量,以轴承轴向刚度、径向刚度作为输出量.
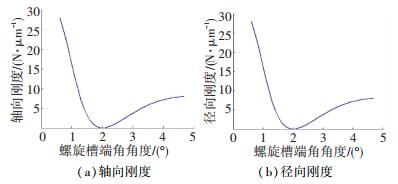
图 7是以螺旋槽倾角为变量的轴承分析结果.由图可知,螺旋槽倾角对半球轴承的轴、径向刚度影响是呈非线性的,主要影响轴承的轴向承载能力,螺旋倾角在20°左右时对轴承力学能力贡献最大.在倾角较小时,若转子转速一定,则螺旋槽的进气量相对较小,造成轴承润滑面压力区增压受限,刚度很低;当倾角很大时,螺旋槽槽口沿转子旋转方向的有效截面很小,同样造成进气量小,内部升压不够,从而影响轴承力学能力.

|
图 7 螺旋槽倾角影响规律 Figure 7 Effective regular of the spiral groove tilt |
图 8为以半球小端止角为变量的轴承分析结果,图中半球小端止角对轴承力学性能基本呈现线性的影响规律.分析可知,半球小端止角主要影响轴承的润滑面积以及轴承出气口的流量,当夹角越小轴承润滑面积越大,轴承增压区域越大,同时在相同进气量的情况下,轴承润滑面气体体积越大,造成压力升高,刚度增加.

|
图 8 半球小端止角影响规律 Figure 8 Effective regular of the hemispheric small end angle |
图 9为以螺旋槽小端止角为变量的轴承分析结果,图中螺旋槽小端止角对轴承的轴、径向刚度影响是呈非线性的,其有一极值点,通常螺旋槽槽底是轴承压力最高区域.然而当螺旋槽小端角度很大时,造成槽底位置与轴承出口压力区接近,使得轴承压力却很快降到电机外部压力,这样在整个轴承润滑面的压力积分将会很小.

|
图 9 螺旋槽小端止角影响规律 Figure 9 Effective regular of the spiral groove small end angle |
图 10是以螺旋槽深度为变量的轴承分析结果,当螺旋槽的深度很小时,虽然有助于轴承的力学能力,但是考虑到动压气体轴承涡动效应的存在,一般选择大于轴承间隙(2 μm)的区间.随着螺旋槽深度的增加,轴承刚度也在增加,直到不再增长,如果继续增加槽深,轴承刚度便开始出现下降趋势,这主要是因为槽深影响轴承进气量,当槽深超过最大值时,轴承内部压缩系数会急剧降低,导致轴承不能承载.
|
图 10 螺旋槽槽深影响规律 Figure 10 Effective regular of the spiral groove depth |
图 11为以螺旋槽槽台比为变量的轴承分析结果.当轴承的结构尺寸一定时,其槽台比对轴承刚度的影响如图 11所示,当槽台比值在1左右(槽宽比值此时为0.5)时,即螺旋槽槽区和台区宽度相等,此时动压气体轴承的轴、径向刚度达到最大值.

|
图 11 螺旋槽槽台比影响规律 Figure 11 Effective regular of the spiral groove width ratio |
综合以上分析结果,就可进一步确定出半球型动压气体轴承螺旋槽的各参数.
2.4 陀螺电机工况下轴承微变形仿真分析动压气体轴承定子、转子之间的机械间隙非常重要,如选取不合适,会导致在电机工作中出现轴承接触、卡滞等故障模式.下面将通过有限元方法主要对电机转子在高速离心作用下产生的微变形以及在陀螺工作温度下轴承零件工作面的微变形等进行仿真分析,以避免出现轴承定、转子在同步运转工况下产生接触卡滞的问题.
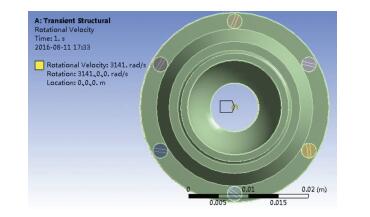
2.4.1 高速运转离心作用下的转子变形如图 12所示,在有限元软件中建立转子分析模型,设置转子的轴承盖材料为GT35,转子壳体为1J50,螺钉为TC4,转子磁钢为钐钴永磁合金,轴承设计工作间隙理论为2 μm.以转子磁钢内表面为参考面,设置转子沿转子轴向的旋转角速度30 000 r/min,设置转子各零件接触面的约束.
|
图 12 转子力学约束 Figure 12 Mechanical constraint of the motor rotor |
图 13是转子在承受30 000 r/min的转速下,轴承转子盖上的变形情况,在轴承转子盖与转子壳体配合处的变形量为0.137 μm,在轴承转子盖工作面上的变形量为0.143 μm,轴承转子盖最大变形发生在转子盖端部外圆处,约为0.204 μm.

|
图 13 转子盖的变形 Figure 13 Distortions of the motor rotor cover |
由于一般半球动压电机的轴承零件形位精度都设计在0.3 μm左右,再加上在高速离心作用下其轴承工作面的结构变形是通过质心沿着轴向产生的.
由此可见,本文设计的半球型动压气体轴承陀螺电机在30 000 r/min同步运转离心作用下产生的微变形对轴承的机械间隙影响很小,不会带来轴承定、转子间隙为零或过盈的情形.
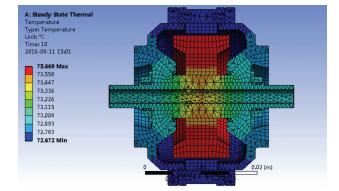
2.4.2 热变形仿真分析半球动压电机是处于常温条件下进行测试和装配,然而在陀螺环境中,电机工作环境温度为65 ℃,加上电机本身的发热,电机内部形成一定的温度梯度.电机在工作温度场达到稳态的情况下,电机内部的温度分布情况如图 14所示.
|
图 14 陀螺电机温度分布 Figure 14 Thermal strain diagram of the gyro motor |
从图中可以看出,电机定子的电枢绕组部分的温度最高,其次是定子轴、左右半球、转子盖,在温度场达到稳态的情况下,电机定子绕组位置的最高温度达到73.7 ℃.
计算电机的热通量,如图 15所示,可以看到电机最大热通量发生在半球与轴的配合面处,最大热通量为14 240 W/m2.

|
图 15 电机热通量分布 Figure 15 Heat flux steady state diagram of the gyro motor |
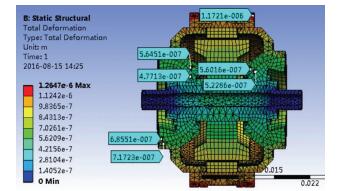
将电机的热稳态分析结果作为边界条件,对电机的应力变形情况进行分析,如图 16所示,可以看到电机在轴承工作面附近位置,其应力变形在0.4~0.7 μm之内,并且转子盖的变形量比半球的变形量大0.1 μm左右,这样可得出动压陀螺电机在工作温度下其轴承工作面的变形最大在0.6 μm左右,因此不会带来轴承定、转子间隙为零或过盈的情形.
|
图 16 陀螺工作温度下的电机热变形情况 Figure 16 Heat distortion diagram of the gyro motor at the operating temperature |
根据以上对半球型动压气体轴承永磁陀螺电机轴承材料选用、螺旋槽关键参数的设计以及保证电机可靠启停的各种工况下轴承微变形仿真分析结果来看,半球动压电机各项参数设计合理,不会带来轴承定、转子间隙为零或过盈的情形.
3 半球动压电机的验证试验某型半球动压电机轴承主要设计参数:半球半径为7.8 mm,轴承间隙为2 μm,螺旋槽数为12,半球小端止角为26°,螺旋槽小端止角为57°,螺旋槽倾角为27°,槽深3 μm,槽宽比为0.5.研制的3块半球型动压气体轴承陀螺电机样机(编号为1#、2#、3#)实物如图 17所示.

|
图 17 半球动压电机样机实物图 Figure 17 Figure of hemispheric aerodynamic bearing motor |
陀螺电机样机在电气参数测试情况如表 1所示.表中H方向是指陀螺电机的动量矩方向,要求启动电流IA0、IB0、IC0均小于750 mA,启动功率小于10 W,同步时间小于30 s,工作电流IA、IB、IC均要小于150 mA,工作功率小于3.8 W,惯性时间大于70 s,其中动压气体轴承的静摩擦力矩主要通过反力矩测试仪设备来完成测试,图 18为电机反力矩测试的力矩与时间关系曲线.
| 表 1 3台陀螺电机H水平电气参数测试情况 Table 1 Electrical parameters test data of three gyro motors |

|
图 18 实测电机力矩与时间关系 Figure 18 Figure of relationship between moment and time |
将陀螺电机装入试验专用的密封罐内,然后将装有电机专用密封罐放置在高温箱内,高温箱供电,使箱内温度达到(65±2)℃,保温30 min,启动电机,电机同步后,运转30~50 s,断开电机电源,电机完全停转后,再对电机进行下一次启、停.试验方向按电机动量矩水平方向进行.
3台试验电机目前已完成了3 000次的启停试验,试验过程中电机性能正常,无启停故障记录.试验后电机测试数据如表 2所示,其工作功率、惯性时间等参数均无明显变化.目前启停寿命试验仍继续进行,已完成4 663次,从目前试验数据和结果可得出,半球动压电机样机可满足高精度三浮陀螺仪表提出的不少于3 000次的启停次数要求.
| 表 2 3台陀螺电机启停试验后H水平测试情况 Table 2 Electrical parameters test data of three gyro motors |
研制了半球型动压气体轴承永磁陀螺电机, 支承采用对置半球型动压气体轴承.通过对关键的动压气体轴承螺旋槽参数和轴承工作间隙进行设计、仿真优化分析,进一步保证了半球动压电机能可靠启停.研制的半球动压电机样机通过了专项的启停试验验证,试验数据表明提出的半球动压电机以及动压气体轴承设计方法正确可行,这些都为后续半球型动压气体轴承陀螺电机的工程化提供了参考价值.
| [1] |
李明德. 费伦梯公司访问随记:陀螺研制概况[J].
控制工程, 1989(1): 31-39.
LI Mingde. The randomness of the visit to Fei Lun Ladder company: the survey of gyro development[J]. Control Engineering, 1989(1): 31-39. |
| [2] |
BREADMAN G. Development of the series 700 gas bearing gyroscope[C]//5th International Gas Bearing Symposium. Southampton: University of Southampton, 1971: 16-29.
|
| [3] |
李建春, 曹清. 陀螺电机的发展趋势[J].
导航与控制, 2004, 3(2): 63-66.
LI Jianchun, CAO Qing. Developing trend of the gyro motor[J]. Navigation and Control, 2004, 3(2): 63-66. |
| [4] |
王京锋, 刘景林, 许卫刚. 动压气体轴承陀螺电机技术发展综述[J]. 微电机, 2016, 49(3): 90-94.
WANG Jingfeng, LIU Jinglin. The development and application of technology of the dynamic hydrodynamic gas bearing gyroscope motor [J]. Micromotors, 2016, 49(3): 90-94. http: //kns. cnki. net/KCMS/detail/detail. aspx?filename=wdjz201603021&dbname=CJFD&dbcode=CJFQ |
| [5] |
李建春, 冯浩, 王晓瑜, 等. 气体动压轴承技术在陀螺电机中的应用[J].
微电机, 2012, 45(6): 80-82.
LI Jianchun, FENG Hao, WANG Xiaoyu. Application of gas-dynamic bearing in gyro motor[J]. Micromotors, 2012, 45(6): 80-82. |
| [6] |
王晓瑜. 研具对半球型动压气浮轴承球面成型精度的影响[J].
导航与控制, 2010, 9(1): 50-56.
WANG Xiaoyu. The influence of abrasive tool on sphericity of semi-sphere for dynamic gas-bearing with sphere forming[J]. Navigation and Control, 2010, 9(1): 50-56. |
| [7] |
边新孝, 李谋渭, 李威. 加工误差对气体静压径向轴承的影响[J].
北京科技大学学报, 2005, 27(3): 331-333.
BIAN Xingxiao, LI Mouwei, LI Wei. Tolerance effect on performance of extemally pressurized air joumal bearings[J]. Journal of University of Science and Techoology Beijing, 2005, 27(3): 331-333. |
| [8] |
姚英学, 杜建军, 刘暾, 等. 制造误差对气体静压轴颈-止推轴承静特性影响[J].
哈尔滨工业大学学报, 2003, 35(1): 315-318.
YAO Yingxue, DU Jingjun, LIU Dun, et al. Effect of manufacturing errors on static characteristics of externally pressurized gas journal-thrust bearing[J]. Journal of Harbin Institute of Technology, 2003, 35(1): 315-318. |
| [9] |
贾晨辉, 杨伟, 邱明. 螺旋槽动压气体轴承的多目标优化设计[J].
机床与液压, 2014, 42(15): 63-67.
JIA Chenhui, YANG Wei, QIU Ming. Multi-objective optimization design of spiral groove aerodynamic Bearings[J]. Machine Tool & Hydraulics, 2014, 42(15): 63-67. DOI: 10.3969/j.issn.1001-3881.2014.15.016 |
| [10] |
朱新龙, 孙军, 张亮, 等. 气体轴承润滑研究的现状及展望[J].
机械设计, 2015, 32(1): 1-5.
ZHU Xinglong, SUN Jun, ZHANG Liang, et al. Review on lubrication of gas bearing[J]. Journal of Machine Design, 2015, 32(1): 1-5. |
| [11] |
秦和平. 柱型动压马达吸合效应机理分析及解决办法[C]//惯性技术发展动态发展方向研讨会. 北京: 中国惯性技术学会, 2010: 98-99.
QIN Heping. Adhesion effect in gas dynamic bearing [C]//Seminar on development and application of inertial technology. Beijing: Chinese Society of Inertial Technology, 2010: 98-99. http: //cpfd. cnki. com. cn/Article/CPFDTOTAL-ZGGZ201006001019. htm |
| [12] |
WANG Jingfeng, LIU Jinglin, YAN Yachao. Improved stiffness test method for gas-dynamic bearing of gyro motor[J].
Journal of Chinese Inertial Technology, 2016, 24(2): 245-250.
|
| [13] |
孙丽, 张俊. 陀螺用H型动压气浮轴承电机启动特性[J].
空间控制技术与应用, 2012, 38(5): 53-56.
SUN Li, ZHANG Jun. Starting characteristics of gyro-used"H"type hydrodynamic air bearing[J]. Aerospace Control and Application, 2012, 38(5): 53-56. |
| [14] |
王京锋, 刘景林, 卜石. 动压气体轴承陀螺电机启停可靠性分析研究[J].
微特电机, 2016, 44(6): 17-22.
WANG Jingfeng, LIU Jinglin, BU Shi. The study of the start and stop reliability of a dynamic hydrodynamic gas bearing gyroscope motor[J]. Small & Special Electrical Machines, 2016, 44(6): 17-22. |
| [15] |
LEE K S, KIM S, LEE D. Aerodynamic focusing of 5-50 nm nanoparticles in air[J].
Journal of Aerosol Science, 2009, 40(12): 1011-1018.
|
| [16] |
AWASTHI R K, JAIN S C, SATISH C, et al. Finite element analysis of orifice-compensated multiple hole-entry worn hybrid journal bearing[J].
Finite Elements in Analysis and Design, 2006, 42(14/15): 1291-1303.
|
 2017, Vol. 49
2017, Vol. 49


