2. 南京晓庄学院 信息工程学院,南京 211171
2. School of Electronic Engineering, Nanjing Xiaozhuang University, Nanjing 211171, China
随着无人机的广泛应用,任务需求的扩展,机动飞行能力正逐渐成为无人机的基本性能要求[1-3].机动飞行能力可以使无人机规避地面防空武器打击,提高战场生存力,并且是执行快速移动目标监视和打击、拦截巡航导弹、舰上着陆的基本保障[4-5].近年来,随着矢量技术和控制技术的发展,以及作战环境的需求,飞翼无人机的机动能力受到了前所未有的重视[6-7].
同常规布局飞机相比,飞翼布局飞行器具有结构、气动和隐身方面的优势,但是并不适合机动飞行[8-10].由于特殊的气动布局,飞翼无人机在机动飞行过程中的纵、横向通道间相互耦合比常规布局飞机更加严重.同时,复杂的非线性,迟滞效应,不确定扰动等问题,使得飞翼无人机的机动控制很困难[11-13].以配平函数得到的平衡点状态模型不能完全反映无人机的机动飞行特性[14-15],工程应用的PID设计方法在此时失去了作用.因此,需要针对飞翼无人机在机动飞行时具体的状态特性研究更有效的设计方法,在保证无人机飞行品质的同时,具有较好的鲁棒性能.
飞翼无人机机动飞行是典型的强耦合非线性控制问题,首要问题是消除非线性因素对飞行指令响应的影响.文献[16-25]研究非线性控制方法在飞行控制设计上的应用问题,并在实践中得到了验证.
根据飞翼无人机的具体特性,本文设计了内环线性化解耦以消除已知不利的耦合项,外环反步跟踪方法进行航迹跟踪的控制结构,并在文中证明了该控制结构的稳定性.同传统反步控制方法相比,本控制器增加了内环解耦结构.不同与传统的动态逆解耦控制方法,本文在控制结构中保留气动阻尼项,使得线性化后的系统为弱非线性系统.该结构不仅可以降低外环控制器设计的保守性,而且便于工程实现.通过飞翼无人机模型的自主飞行试验,验证了该设计方法是有效的.
1 研究对象本文研究对象为带有推力矢量方向舵的缩比验证飞翼无人机.该无人机的实物如图 1所示.

|
图 1 无人机实物照片 Figure 1 Photo by flying-wing UAV |
该无人机的翼展823 mm,机身长1 077 mm.机载传感器设备包括陀螺仪、加速度计、GPS接收机.探测器和动力采用两个电池组驱动.全机和各种机载设备的总重为2.2 kg.该无人机的舵面如图 2所示.

|
图 2 无人机控制舵面分布 Figure 2 UAV control rudder |
如图 2所示,该无人机采用双涵道螺旋桨提供动力.单个涵道螺旋桨发动机可以提供13 N的推力.全机的推重比为1.20.在涵道出气口处安装有可调节的挡板,该装置用来改变气流的方向,起到矢量方向舵的作用.机翼后端各有一片升降副翼.这两片舵面同向作用时为升降舵,差动时作为副翼使用.
2 飞翼无人机气动建模由于该无人机采用特殊的矢量式方向舵,这里首先对矢量式方向舵进行建模.矢量舵两片挡板只能向同一方向偏转.由于布局的限制,两片挡板中只有向机身中线偏转的一片改变气流的方向.假设,气流沿挡板流动,则矢量式方向舵产生的侧力和偏航力矩为
| $ \left\{ \begin{array}{l} {f_{\rm{N}}} = {f_T}\sin {\delta _{\rm{r}}} \approx {f_{\rm{T}}}{\delta _{\rm{r}}},\\ {M_{\rm{N}}} = {f_{\rm{T}}}{l_1}\sin {\delta _{\rm{r}}} \approx {f_{\rm{T}}}{l_1}{\delta _{\rm{r}}}. \end{array} \right. $ | (1) |
式中:fT为单涵道提供的推力,l1为挡板沿机身方向到重心的距离,δr为挡板的偏转角.
根据具体的研究对象,飞翼无人机的仿射非线性模型为
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\dot p}\\ {\dot q}\\ {\dot r} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{c_2}pq + {c_1}qr}\\ {{c_5}pr - {c_6}\left( {{P^2} - {r^2}} \right)}\\ { - {c_2}qr + {c_8}pq} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{c_3}{C_1}\bar qSb + {c_4}{C_{\rm{n}}}\bar qSb}\\ {{c_7}{C_{\rm{m}}}\bar qS\bar c}\\ {{c_4}{C_1}\bar qSb + {c_9}{C_{\rm{n}}}\bar qSb} \end{array}} \right] + \\ \frac{{\rho VS}}{4}\left[ {\begin{array}{*{20}{c}} {{c_3}{C_{{\rm{lp}}}}b + {c_4}{C_{{\rm{np}}}}b}&0&{{c_3}{C_{{\rm{lr}}}}b + {c_4}{C_{{\rm{nr}}}}b}\\ 0&{{c_7}{C_{{\rm{mq}}}}\bar c}&0\\ {{c_4}{C_{{\rm{lp}}}}b + {c_9}{C_{{\rm{np}}}}b}&0&{{c_4}{C_{{\rm{lr}}}}b + {c_9}{C_{{\rm{nr}}}}b} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} p\\ q\\ r \end{array}} \right] + \\ \bar qS\left[ {\begin{array}{*{20}{c}} 0&{{c_3}{C_{{\rm{l \mathit{ δ} a}}}}b + {c_4}{C_{{\rm{n \mathit{ δ} a}}}}b}&{{c_3}{C_{{\rm{l \mathit{ δ} a}}}}b}\\ {{c_7}{C_{{\rm{m \mathit{ δ} e}}}}\bar c}&0&0\\ 0&{{c_4}{C_{{\rm{l \mathit{ δ} a}}}}b}&{{c_4}{C_{{\rm{l \mathit{ δ} a}}}}b + {M_N}/\bar qS} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\delta _{\rm{e}}}}\\ {{\delta _{\rm{a}}}}\\ {{\delta _{\rm{r}}}} \end{array}} \right]. \end{array} $ | (2) |
| $ \left[ {\begin{array}{*{20}{c}} {\dot \varphi }\\ {\dot \theta }\\ {\dot \psi } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&{\sin \varphi \tan \varphi }&{\cos \varphi \tan \theta }\\ 0&{\cos \varphi }&{ - \sin \varphi }\\ 0&{\sin \varphi /\cos \theta }&{\cos \varphi /\cos \theta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} p\\ q\\ r \end{array}} \right]. $ | (3) |
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\dot \alpha }\\ {\dot \beta }\\ {\dot \varphi } \end{array}} \right] = \frac{1}{{mV}}\left[ {\begin{array}{*{20}{c}} { - \sin \alpha \left( {T + {C_{\rm{x}}}\bar qS} \right)/\cos \beta + \cos \alpha {C_{\rm{z}}}\bar qS/\cos \beta }\\ { - \cos \alpha \sin \beta \left( {T + {C_{\rm{x}}}\bar qS} \right) + \cos \beta {C_{\rm{y}}}\bar qS - \sin \alpha \sin \beta {C_{\rm{z}}}\bar qS}\\ 0 \end{array}} \right] + \\ \left[ {\begin{array}{*{20}{c}} { - \cos \alpha \tan \beta }&1&{ - \sin \alpha \tan \beta }\\ {\sin \alpha }&0&{ - \cos \alpha }\\ 1&{\sin \varphi \tan \theta }&{\cos \varphi \tan \theta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} p\\ q\\ r \end{array}} \right] + }\\ {\frac{{\rho S}}{{4m}}\left[ {\begin{array}{*{20}{c}} 0&{ - \sin \alpha {C_{{\rm{xq}}}}\bar c/\cos \beta + \cos \alpha {C_{{\rm{zq}}}}\bar c/\cos \beta }&0\\ {\cos \beta {C_{{\rm{yp}}}}b}&{ - \cos \alpha \sin \beta {C_{{\rm{xq}}}}\bar c - \sin \alpha \sin \beta {C_{{\rm{zq}}}}\bar c}&{\cos \beta {C_{{\rm{yr}}}}b}\\ 0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} p\\ q\\ r \end{array}} \right] + }\\ {\frac{{\rho VS}}{{2m}}\left[ {\begin{array}{*{20}{c}} { - \sin \alpha {C_{{\rm{x \mathit{ δ} e}}}}/\cos \beta + \cos \alpha {C_{{\rm{z \mathit{ δ} e}}}}/\cos \beta }&0&0\\ { - \cos \alpha \sin \beta {C_{{\rm{x \mathit{ δ} e}}}} - \sin \alpha \sin \beta {C_{{\rm{z \mathit{ δ} e}}}}}&{ - \cos \beta {C_{{\rm{y \mathit{ δ} a}}}}}&0\\ 0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\delta _{\rm{e}}}}\\ {{\delta _{\rm{a}}}}\\ {{\delta _{\rm{r}}}} \end{array}} \right] + }\\ {\frac{g}{V}\left[ {\begin{array}{*{20}{c}} {\left( {\sin \alpha \sin \theta + \cos \alpha \cos \varphi \cos \theta } \right)/\cos \beta }\\ {\cos \alpha \sin \beta \sin \theta + \cos \beta \cos \theta \sin \varphi - \sin \alpha \sin \beta \cos \varphi \cos \theta }\\ 0 \end{array}} \right].} \end{array} $ | (4) |
以上各式均采用欧美体系惯用方式,各符号具体定义可参照参考文献[4-5].定义状态向量x1, x2, x3, u∈R3,且x1=[α, β, φ]T,x2=[p, q, r]T,x3=[φ, θ, ψ]T,u=[δe, δa, δr]T,定义x4=[x1, x2]T,x5=[x2, x3]T,可得动态方程为
| $ {{\mathit{\boldsymbol{\dot x}}}_1} = {f_1}\left( {{\mathit{\boldsymbol{x}}_1}} \right) + {g_{{\rm{s}}1}}\left( {{\mathit{\boldsymbol{x}}_4}} \right){\mathit{\boldsymbol{x}}_2} + {g_{{\rm{s}}2}}\left( {{\mathit{\boldsymbol{x}}_4}} \right)\mathit{\boldsymbol{u}}, $ | (5) |
| $ {{\mathit{\boldsymbol{\dot x}}}_2} = {f_{\rm{f}}}\left( {{\mathit{\boldsymbol{x}}_4}} \right) + {g_{\rm{f}}}\left( {{\mathit{\boldsymbol{x}}_4}} \right)\mathit{\boldsymbol{u}}. $ | (6) |
为了内环解耦设计表述方便,无人机的姿态方程为
| $ {{\mathit{\boldsymbol{\dot x}}}_5} = {f_{\rm{t}}}\left( {{\mathit{\boldsymbol{x}}_5}} \right) + {g_{\rm{t}}}\left( {{\mathit{\boldsymbol{x}}_5}} \right)\mathit{\boldsymbol{u}}. $ | (7) |
内环姿态控制的好坏直接决定了外环航路跟踪的品质和精确性.飞行器飞行的首要任务是保持系统的稳定性,气动阻尼项是评判系统稳定性的重要指标.
与常规布局的飞行器相比,飞翼布局无人机间的耦合效应更加严重.而且,飞翼布局无人机稳定性差,舵面操作效率不足.这些因素使得无人机在机动飞行中的飞行品质难以保证.通常的线性化方法总是消除无人机所有的非线性项.其中就包括反映无人机阻尼特性的气动阻尼项,该项对无人机的稳定飞行是有利的.在无人机内环解耦过程中,保留气动阻尼项具有实际意义.此时得到系统是包含时变参数的弱非线性伪线性系统.该处理方式不仅保留了一部分系统的气动阻尼特性,减弱了传统动态逆方法设计中的“微分爆炸问题”.
根据该思想,本文的内环解耦控制器设计时,增加了气动补偿模块;该气动补偿模块消除了飞行过程中的气动耦合和惯性耦合项,却在控制结构中保留气动阻尼项,使得线性化后的系统为弱非线性系统;在此基础上,设计了理论严谨的利于李导数的微分几何解耦方法,消除了运动耦合项.经过内环解耦后的系统表现为弱非线性.在外环控制上,设计反步跟踪外环控制器,以保证无人机快速精确的响应飞行指令.本文设计的控制器结构如图 3所示.

|
图 3 制器结构图 Figure 3 Controller structure diagram |
在图 3所示的控制结构中,为克服动态逆方法对建模精度要求高的不足,本文内环解耦线性化控制器采用基于气动数据库的李导数解耦方法.在该结构中,气动数据库在线补偿与无人机动力学模型组成伪控制对象,外环反步跟踪控制器与该伪控制对象串联组成闭环系统.
该方法降低系统的运算量.该处理方法可以降低控制器设计的保守性,而且便于工程实现.
4 姿态方程的线性化解耦 4.1 保留气动阻尼项的力矩补偿根据上节的论述可知,保留气动力矩阻尼项的解耦线性化可以带来很多益处.因此本节介绍保留气动阻尼项的力矩补偿方法.由图 3的控制器结构,其内环非线性解耦模块更具体的结构如图 4所示.

|
图 4 内环非线性解耦模块结构 Figure 4 Structure of the in-loop nonlinear decoupling module |
为了表述方便,这里把无人机的姿态方程表述为
| $ \mathit{\boldsymbol{\dot \omega }} = - {\mathit{\boldsymbol{I}}^{ - 1}}\mathit{\boldsymbol{S}}\left( \omega \right)\mathit{\boldsymbol{I\omega }} + {\mathit{\boldsymbol{I}}^{ - 1}}{\mathit{\boldsymbol{M}}_{\rm{A}}}. $ | (8) |
其中:ω=[p, q, r]T,MA为空气动力产生的力矩,I和S(ω)分别为惯性矩阵和ω的反对称矩阵,即
| $ \mathit{\boldsymbol{I}} = \left[ {\begin{array}{*{20}{c}} {{I_x}}&0&{ - {I_{xz}}}\\ 0&{{I_y}}&0\\ { - {I_{xz}}}&0&{{I_z}} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{S}}\left( \mathit{\boldsymbol{\omega }} \right) = \left[ {\begin{array}{*{20}{c}} 0&{ - r}&q\\ r&0&{ - p}\\ { - q}&p&0 \end{array}} \right]. $ |
式(8)中气动力矩可为
| $ V{M_{\rm{A}}} = {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}\left( {{c_x}} \right){\varphi _1} + {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}\left( {{c_x}} \right){\delta _{\rm{A}}}. $ | (9) |
其中:
| $ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}\left( {{c_x}} \right) = QS\left[ {\begin{array}{*{20}{c}} b&0&0\\ 0&{\bar c}&0\\ 0&0&b \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{C_{l0}}}&0&{C_l^\beta }&{C_l^p}&0&{C_l^r}\\ {{C_{m0}}}&{C_m^\alpha }&0&0&{C_m^q}&0\\ {{C_{n0}}}&0&{C_n^\beta }&{C_n^p}&0&{C_n^r} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}\left( {{c_x}} \right) = QS\left[ {\begin{array}{*{20}{c}} { - b}&0&0\\ 0&{\bar c}&0\\ 0&0&b \end{array}} \right]\left[ {\begin{array}{*{20}{c}} { - C_l^{{\delta _{\rm{a}}}}}&0&{C_l^{{\delta _{\rm{r}}}}}\\ 0&{C_m^{{\delta _{\rm{e}}}}}&0\\ {C_n^{{\delta _{\rm{a}}}}}&0&{C_n^{{\delta _{\rm{e}}}}} \end{array}} \right]. $ |
| $ {\mathit{\boldsymbol{\delta }}_A} = {\left[ {\begin{array}{*{20}{c}} {{\delta _{\rm{a}}}}&{{\delta _{\rm{e}}}}&{{\delta _{\rm{r}}}} \end{array}} \right]^{\rm{T}}},{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_1} = {\left[ {\begin{array}{*{20}{c}} 1&\alpha &\beta &p&q&r \end{array}} \right]^{\rm{T}}}. $ |
假设气动力矩系数为含有时变参数摄动非线性函数
| $ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i} = \mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }} + \Delta {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i},i = 1,2. $ | (10) |
其中:
将式(10)代入式(8)可得
| $ \dot \omega = \bar f + \Delta f + \left[ {\bar g + \Delta g} \right]{\delta _{\rm{A}}}. $ | (11) |
其中:f=-I-1S(ω)Iω+I-1
| $ \Delta \bar f = {\mathit{\boldsymbol{I}}^{ - 1}}\Delta {{\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}}_1}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_1},\bar g = {\mathit{\boldsymbol{I}}^{ - 1}}{{\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}}_2},\Delta \bar g = {\mathit{\boldsymbol{I}}^{ - 1}}\Delta {{\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}}_2}. $ |
则系统的标称模型可表示为
| $ \begin{array}{*{20}{c}} {\dot \omega = - {\mathit{\boldsymbol{I}}^{ - 1}}\mathit{\boldsymbol{S}}\left( \mathit{\boldsymbol{\omega }} \right)\mathit{\boldsymbol{I\omega }} + {\mathit{\boldsymbol{I}}^{ - 1}}{{\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}}_1}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_1} - \mathit{\boldsymbol{\bar K\omega }} + {I^{ - 1}}{{\mathit{\boldsymbol{\bar M}}}_{T0}} + }\\ {\mathit{\boldsymbol{\bar K\omega }} + {\mathit{\boldsymbol{u}}_{{\rm{cm}}}} + {\mathit{\boldsymbol{u}}_{{\rm{lin}}}} = {f_0} + \mathit{\boldsymbol{\bar Kw + }}{\mathit{\boldsymbol{u}}_{{\rm{cm}}}} + {\mathit{\boldsymbol{u}}_{{\rm{lin}}}}.} \end{array} $ | (12) |
其中:f0=f-Kω表示需要进行补偿的惯性耦合力矩、气动耦合力矩和推力附加力矩;K=diag(k1, k2, k3)为各通道对应的阻尼力矩系数的标称值,k1=h11lp+h13np,k2=h22mp,k3=h31lr+h33nr,hij(i, j=1, 2, 3)为惯性矩阵I-1的第i行和第j列分量.
由于阻尼力矩反映了无人机本体固有的阻尼特性,因此,在气动补偿过程这部分力矩应保留下来.则补偿力矩可为
| $ {\mathit{\boldsymbol{u}}_{{\rm{cm}}}} = {\mathit{\boldsymbol{I}}^{ - 1}}\left[ {\mathit{\boldsymbol{S}}\left( \mathit{\boldsymbol{\omega }} \right)\mathit{\boldsymbol{I\omega }} - {{\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}}_1}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_1}} \right] + \mathit{\boldsymbol{\bar K}}\omega . $ | (13) |
通过上式力矩补偿可以抵消惯性耦合力矩和通道间的交叉耦合力矩对系统的影响,当无人机进行大角速度机动时,可以避免各通道间产生耦合.
将式(10)代入式(9)得
| $ \mathit{\boldsymbol{\dot \omega }} = \bar k\mathit{\boldsymbol{\omega }} + {\mathit{\boldsymbol{u}}_{{\rm{lin}}}}. $ | (14) |
而由式(14)可知,该补偿方式最后得到一个一阶惯性环节.该惯性环节保留了系统固有的阻尼特性,以ulin为控制量可以进一步设计控制器可以保证系统具有较好的闭环性能.
4.2 姿态方程的线性化为使系统更好地响应指令,这里对无人机的姿态方程进行线性化处理.这里采用基于李导数的输入输出线性化方法.系统的线性化步骤如下.
1) 选择定义在x°邻域的坐标变换函数集
| $ \xi _k^i\left( k \right) = \varphi _k^i\left( x \right) = L_f^{k - 1}{h_i}\left( x \right). $ | (15) |
其中1≤k≤ri,1≤i≤m.
2) 把系统变换为m组方程
| $ \left\{ \begin{array}{l} \xi _1^i = \xi _2^i,\\ \vdots \\ \xi _{{r_i} - 1}^i = \xi _{{r_i}}^i,\\ \xi _{{r_i}}^i = {b_i}\left( \xi \right) + \sum\limits_{j = 1}^m {{a_{ij}}\left( \xi \right){u_j}} . \end{array} \right. $ | (16) |
式中:
| $ {b_i}\left( \xi \right) = L_f^{{r_i}}{h_i}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}}\left( \xi \right)} \right), $ |
| $ {a_{ij}}\left( \xi \right) = {L_{{g_j}}}L_f^{{r_i} - 1}{h_i}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}}\left( \xi \right)} \right), $ |
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( x \right) = {\left[ {\varphi _1^1\left( x \right), \cdots ,\varphi _{{r_1}}^1\left( x \right), \cdots ,\varphi _1^m\left( x \right), \cdots ,\varphi _{{r_m}}^m\left( x \right)} \right]^{\rm{T}}}. $ |
3) 把式
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\dot \xi _{{r_1}}^1}\\ \vdots \\ {\dot \xi _{{r_m}}^m} \end{array}} \right] = \mathit{\boldsymbol{b}}\left( \xi \right) + \mathit{\boldsymbol{A}}\left( \xi \right)\mathit{\boldsymbol{u}} = \left[ {\begin{array}{*{20}{c}} {{b_1}\left( \xi \right)}\\ \vdots \\ {{b_m}\left( \xi \right)} \end{array}} \right] + \\ \;\;\left[ {\begin{array}{*{20}{c}} {{a_{11}}\left( \xi \right)}& \cdots &{{a_{1m}}\left( \xi \right)}\\ \vdots &{}& \vdots \\ {{a_{m1}}\left( \xi \right)}& \cdots &{{a_{mm}}\left( \xi \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_1}}\\ \vdots \\ {{u_m}} \end{array}} \right]. \end{array} $ | (17) |
令b(ξ)+A(ξ)u=v=[v1…vm]T, 可解得精确线性化的反馈为
| $ {\mathit{\boldsymbol{u}}_l} = {\mathit{\boldsymbol{A}}^{ - 1}}\left( \xi \right)\left[ { - \mathit{\boldsymbol{b}}\left( \xi \right) + \mathit{\boldsymbol{v}}} \right]. $ | (18) |
经过以上坐标变换和状态反馈,原系统变换为Brunovsky标准形系统
| $ \left\{ \begin{array}{l} \dot \xi _1^i = \xi _2^i,\\ \;\;\;\; \vdots \\ \dot \xi _{{r_i} - 1}^i = \xi _{{r_i}}^i,\\ \dot \xi _{{r_i}}^i = {v_i}. \end{array} \right. $ | (19) |
经过以上步骤,可将仿射系统变换为标准线性系统.
根据式(16),可得系统的坐标变换函数为
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( x \right) = \left[ {\begin{array}{*{20}{c}} \varphi \\ {p + q\sin \varphi \tan \theta + r\cos \varphi \tan \theta }\\ \theta \\ {q\cos \varphi - r\sin \varphi }\\ \psi \\ {q\sin \varphi \sec \theta + r\cos \varphi \sec \theta } \end{array}} \right]. $ | (20) |
由式(16)可得
| $ \mathit{\boldsymbol{a}} = \left[ {\begin{array}{*{20}{c}} {{L_{{g_1}}}{L_f}{\lambda _1}}&{{L_{{g_2}}}{L_f}{\lambda _1}}&{{L_{{g_3}}}{L_f}{\lambda _1}}\\ {{L_{{g_1}}}{L_f}{\lambda _2}}&{{L_{{g_2}}}{L_f}{\lambda _2}}&{{L_{{g_3}}}{L_f}{\lambda _2}}\\ {{L_{{g_1}}}{L_f}{\lambda _3}}&{{L_{{g_2}}}{L_f}{\lambda _3}}&{{L_{{g_3}}}{L_f}{\lambda _3}} \end{array}} \right]. $ | (21) |
| $ \mathit{\boldsymbol{b}} = {\left[ {\begin{array}{*{20}{c}} {L_f^2{\lambda _1}}&{L_f^2{\lambda _2}}&{L_f^2{\lambda _3}} \end{array}} \right]^{\rm{T}}}. $ | (22) |
为了下文控制器设计表述方便,将解耦后的姿态方程和轨迹方程表示如下式,并分别命名为系统1和系统2.
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot x}}}_1} = {f_1}\left( {{\mathit{\boldsymbol{x}}_1}} \right) + {\mathit{\boldsymbol{g}}_{s1}}\left( {{\mathit{\boldsymbol{x}}_4}} \right){\mathit{\boldsymbol{x}}_2} + {g_{s2}}\left( {{\mathit{\boldsymbol{x}}_4}} \right)\mathit{\boldsymbol{u}},\\ {{\mathit{\boldsymbol{\dot x}}}_2} = {f_f}\left( {{\mathit{\boldsymbol{x}}_4}} \right) + {g_f}\left( {{\mathit{\boldsymbol{x}}_4}} \right)\mathit{\boldsymbol{u}}. \end{array} \right. $ | (23) |
其中,状态向量x1, x2, x3, u∈R3,且x1=[α, β, φ]T,x2=[p, q, r]T,x3=[φ, θ, ψ]T,x4=[x1, x2]T,u=[δe, δa, δr, δT]T.
5 外环控制器设计外环控制的目的是实现α, β, φ的输入指令跟踪.外环控制器是根据飞行器的当前状态和输入u输出自适应律,使系统的输出x1渐进跟踪期望的参考输入x1d.
定义估计误差为
| $ \tilde \vartheta = {\vartheta ^ * } - \hat \vartheta , $ | (24) |
| $ \tilde \zeta = {\zeta ^ * } - \hat \zeta . $ | (25) |
式中:
引入误差状态变量
| $ {\mathit{\boldsymbol{z}}_1} = {\mathit{\boldsymbol{x}}_1} - {\mathit{\boldsymbol{x}}_{1d}} = {\left[ {{z_{11}},{z_{21}},{z_{31}}} \right]^{\rm{T}}}, $ | (26) |
| $ {\mathit{\boldsymbol{z}}_2} = {\mathit{\boldsymbol{x}}_2} - {\mathit{\boldsymbol{x}}_{2d}} = {\left[ {{z_{12}},{z_{22}},{z_{32}}} \right]^{\rm{T}}}. $ | (27) |
对上式求导,并代入系统1和系统2可得闭环误差状态方程为
| $ {{\mathit{\boldsymbol{\dot z}}}_1} = {f_1} + {g_{s1}}{\mathit{\boldsymbol{x}}_2} + {\boldsymbol{\vartheta} ^{ * {\rm{T}}}}{\varphi _1} - {{\mathit{\boldsymbol{\dot x}}}_{1d}}, $ | (28) |
| $ {{\mathit{\boldsymbol{\dot z}}}_2} = {f_f} + {g_f}\mathit{\boldsymbol{u}} + {\boldsymbol{\zeta} ^{ * {\rm{T}}}}{\varphi _2} - {{\mathit{\boldsymbol{\dot x}}}_{2d}}. $ | (29) |
由以上两式可得
| $ {{\mathit{\boldsymbol{\dot z}}}_1} = {f_1} + {g_{s1}}{\mathit{\boldsymbol{x}}_{2d}} + {g_{s1}}{\mathit{\boldsymbol{z}}_2} + {\boldsymbol{\vartheta} ^{ * {\rm{T}}}}{\varphi _1} - {{\mathit{\boldsymbol{\dot x}}}_{1d}}. $ | (30) |
定义z1系统的理想控制量为
| $ \mathit{\boldsymbol{x}}_{2d}^ * = g_{s1}^{ - 1}\left( { - {\mathit{\boldsymbol{k}}_1}{\mathit{\boldsymbol{z}}_1} - {f_1} - {\boldsymbol{\vartheta} ^{ * {\rm{T}}}}{\varphi _1} + {{\mathit{\boldsymbol{\dot x}}}_{1d}}} \right). $ | (31) |
式中k1>0为控制器设计参数.由于ϑ*未知,这里用估计值
| $ {\mathit{\boldsymbol{x}}_{2d}} = \mathit{\boldsymbol{g}}_{s1}^{ - 1}\left( { - {\mathit{\boldsymbol{k}}_1}{\mathit{\boldsymbol{z}}_1} - {f_1} - {{\boldsymbol{\hat \vartheta} }^{\rm{T}}}{\varphi _1} + {{\mathit{\boldsymbol{\dot x}}}_{1d}}} \right). $ | (32) |
将上式代入式(30)可得
| $ {{\mathit{\boldsymbol{\dot z}}}_1} = - {\mathit{\boldsymbol{k}}_1}{\mathit{\boldsymbol{z}}_1} + {\mathit{\boldsymbol{g}}_{s1}}{\mathit{\boldsymbol{z}}_2} + {\boldsymbol{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over \vartheta } }}^{\rm{T}}}{\varphi _1}. $ | (33) |
根据式(29), 定义系统的理想控制输入为
| $ {\mathit{\boldsymbol{u}}^ * } = \mathit{\boldsymbol{g}}_f^{ - 1}\left( { - {\mathit{\boldsymbol{k}}_2}{\mathit{\boldsymbol{z}}_2} - {f_f} - \mathit{\boldsymbol{g}}_{s1}^{\rm{T}}{\mathit{\boldsymbol{z}}_1} - {\boldsymbol{\zeta} ^{ * {\rm{T}}}}{\varphi _2} + {{\mathit{\boldsymbol{\dot x}}}_{2d}}} \right). $ | (34) |
类似以上证明过程可得
| $ {\mathit{\boldsymbol{u}}_{\rm{o}}} = \mathit{\boldsymbol{g}}_f^{ - 1}\left( { - {\mathit{\boldsymbol{k}}_2}{\mathit{\boldsymbol{z}}_2} - {f_f} - \mathit{\boldsymbol{g}}_{s1}^{\rm{T}}{\mathit{\boldsymbol{z}}_1} - {\boldsymbol{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}} \over \zeta } }}^{\rm{T}}}{\varphi _2} + {{\mathit{\boldsymbol{\dot x}}}_{2d}}} \right), $ | (35) |
代入式(29)可得
| $ {{\mathit{\boldsymbol{\dot z}}}_2} = - {\mathit{\boldsymbol{k}}_2} - \mathit{\boldsymbol{g}}_{s1}^{\rm{T}}{\mathit{\boldsymbol{z}}_1} + {{\mathit{\boldsymbol{\tilde \zeta }}}^{\rm{T}}}{\varphi _2}. $ | (36) |
由式(19)、(35)可得
| $ {\mathit{\boldsymbol{u}}_{{\rm{lin}}}} = {\mathit{\boldsymbol{u}}_l} + {\mathit{\boldsymbol{u}}_o}. $ |
为了分析系统的稳定性,选取如下Lyapunov函数为
| $ \begin{array}{l} V\left( t \right) = \frac{1}{2}\mathit{\boldsymbol{z}}_1^{\rm{T}}{\mathit{\boldsymbol{z}}_1} + \frac{1}{2}\mathit{\boldsymbol{z}}_2^{\rm{T}}{\mathit{\boldsymbol{z}}_2} + \frac{1}{{2{\lambda _1}}}{\rm{tr}}\left( {{{\boldsymbol{\tilde \vartheta} }^{\rm{T}}}\boldsymbol{\tilde \vartheta} } \right) + \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{{2{\lambda _1}}}{\rm{tr}}\left( {{{\mathit{\boldsymbol{\tilde \zeta }}}^{\rm{T}}}\mathit{\boldsymbol{\tilde \zeta }}} \right) = \frac{1}{2}\mathit{\boldsymbol{z}}_1^{\rm{T}}{\mathit{\boldsymbol{z}}_1} + \frac{1}{2}\mathit{\boldsymbol{z}}_2^{\rm{T}}{\mathit{\boldsymbol{z}}_2} + \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{{2{\lambda _1}}}\left\| {\boldsymbol{ \vartheta} } \right\|_F^2 + \frac{1}{{2{\lambda _1}}}\left\| \mathit{\boldsymbol{\zeta }} \right\|_F^2. \end{array} $ | (37) |
将ϑ*和ζ*表示成分块矩阵的形式,则上式可表示为
| $ \begin{array}{l} V\left( t \right) = \frac{1}{2}\mathit{\boldsymbol{z}}_1^{\rm{T}}{\mathit{\boldsymbol{z}}_1} + \frac{1}{2}\mathit{\boldsymbol{z}}_2^{\rm{T}}{\mathit{\boldsymbol{z}}_2} + \frac{1}{{2{\lambda _1}}}\sum\limits_{i = 1}^3 {\boldsymbol{\tilde \vartheta} _i^{\rm{T}}{{\boldsymbol{\tilde \vartheta} }_i}} + \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{{2{\lambda _2}}}\sum\limits_{i = 1}^3 {\mathit{\boldsymbol{\tilde \zeta }}_i^{\rm{T}}{{\mathit{\boldsymbol{\tilde \zeta }}}_i}} . \end{array} $ | (38) |
对V(t)按时间t求导得
| $ \begin{array}{l} \dot V\left( t \right) = - {\mathit{\boldsymbol{k}}_1}\mathit{\boldsymbol{z}}_1^{\rm{T}}{\mathit{\boldsymbol{z}}_1} - {\mathit{\boldsymbol{k}}_2}\mathit{\boldsymbol{z}}_2^{\rm{T}}{\mathit{\boldsymbol{z}}_2} + \mathit{\boldsymbol{z}}_1^{\rm{T}}{{\boldsymbol{\tilde \vartheta} }^{\rm{T}}}{\varphi _1} + \mathit{\boldsymbol{z}}_2^{\rm{T}}{{\boldsymbol{\tilde \vartheta} }^{\rm{T}}}{\varphi _2} + \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{{{\lambda _1}}}\sum\limits_{i = 1}^3 {\boldsymbol{\tilde \vartheta} _i^{\rm{T}}{{\boldsymbol{\tilde \vartheta} }_i}} + \frac{1}{{{\lambda _2}}}\sum\limits_{i = 1}^3 {\mathit{\boldsymbol{\tilde \zeta }}_i^{\rm{T}}{{\mathit{\boldsymbol{\tilde \zeta }}}_i}} . \end{array} $ | (39) |
令自适应律为
| $ \left\{ \begin{array}{l} {{\dot {\hat \vartheta} }_i} = {\lambda _1}\left( {{\mathit{\boldsymbol{z}}_{i1}}{\varphi _1} - {\alpha _i}{{\boldsymbol{\hat \vartheta} }_i}} \right),\\ {{\dot {\hat \zeta} }_i} = {\lambda _2}\left( {{\mathit{\boldsymbol{z}}_{i2}}{\varphi _2} - {\beta _i}{{\mathit{\boldsymbol{\hat \zeta }}}_i}} \right). \end{array} \right. $ | (40) |
式中:λ1, λ2为大于零的实数,用于调节自适应控制器;
| $ \begin{array}{l} \dot V\left( t \right) = - {\mathit{\boldsymbol{k}}_1}{\left\| {{\mathit{\boldsymbol{z}}_1}} \right\|^2} - {\mathit{\boldsymbol{k}}_2}{\left\| {{\mathit{\boldsymbol{z}}_2}} \right\|^2} + \sum\limits_{i = 1}^3 {{\alpha _i}\boldsymbol{\tilde \vartheta} _i^{\rm{T}}{{\boldsymbol{\tilde \vartheta} }_i}} + \\ \;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^3 {{\beta _i}\mathit{\boldsymbol{\tilde \zeta }}_i^{\rm{T}}{{\mathit{\boldsymbol{\tilde \zeta }}}_i}} = - \left( {{k_{10}} + {k_{11}}} \right){\left\| {{\mathit{\boldsymbol{z}}_1}} \right\|^2} - \left( {{k_{20}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {{k_{21}}} \right){\left\| {{\mathit{\boldsymbol{z}}_2}} \right\|^2} + \sum\limits_{i = 1}^3 {\left( {{\alpha _i}\boldsymbol{\tilde \vartheta} _i^{\rm{T}}{{\boldsymbol{\tilde \vartheta} }_i} + {\beta _i}\mathit{\boldsymbol{\tilde \zeta }}_i^{\rm{T}}{{\mathit{\boldsymbol{\tilde \zeta }}}_i}} \right)} . \end{array} $ | (41) |
由于下面不等式成立:
| $ \boldsymbol{\tilde \vartheta} _i^{\rm{T}}{{\boldsymbol{\tilde \vartheta} }_i} \le 0.5\left( {{{\left\| {\vartheta _i^ * } \right\|}^2} - {{\left\| {{{\tilde \vartheta }_i}} \right\|}^2}} \right), $ |
| $ \mathit{\boldsymbol{\tilde \zeta }}_i^{\rm{T}}\mathit{\boldsymbol{\tilde \zeta }} \le 0.5\left( {{{\left\| {\zeta _i^ * } \right\|}^2} - {{\left\| {{{\tilde \zeta }_i}} \right\|}^2}} \right). $ |
将上式代入(39)式可得
| $ \begin{array}{l} \dot V\left( t \right) \le - {k_{10}}{\left\| {{z_1}} \right\|^2} - {k_{20}}{\left\| {{z_2}} \right\|^2} - \\ \;\;\;\;\;\;\;\;\;\;0.5\sum\limits_{i = 1}^3 {{\alpha _i}{{\left\| {{{\boldsymbol{\tilde \vartheta} }_i}} \right\|}^2}} - \\ \;\;\;\;\;\;\;\;\;\;0.5\sum\limits_{i = 1}^3 {{\beta _i}{{\left\| {{{\mathit{\boldsymbol{\tilde \zeta }}}_i}} \right\|}^2} + \tau } . \end{array} $ | (42) |
式中:
令ρ=min{2k10, 2k20, αi, βi},则式(42)可表示为
| $ \dot V\left( t \right) \le - \rho V\left( t \right) + \tau . $ | (43) |
下面给出并证明如下定理.
定理1 对于系统1和系统2,给定已知的输入参考信号x1d,采用控制律式(35),对于任意给定的初始紧集
| $ {\mathit{\Omega }_0} = \left\{ {{\mathit{\boldsymbol{x}}_{1d}},{\mathit{\boldsymbol{x}}_{2d}},\boldsymbol{\hat \vartheta} ,\mathit{\boldsymbol{\hat \zeta }}\left| {{\mathit{\boldsymbol{x}}_{1d}}\left( 0 \right),{\mathit{\boldsymbol{x}}_{2d}}\left( 0 \right),\boldsymbol{\hat \vartheta} \left( 0 \right),\mathit{\boldsymbol{\hat \zeta }}\left( 0 \right)} \right.} \right\}, $ |
有如下结论.
结论1 闭环系统状态x(t)=[x1T, x2T]T和自适应权值
| $ {\left\| {\boldsymbol{\tilde \vartheta} } \right\|_F} \le {c_{\tilde \vartheta \max }} + {\left\| {{\boldsymbol{\vartheta} ^ * }} \right\|_F}, $ | (44) |
| $ {\left\| {\mathit{\boldsymbol{\hat \zeta }}} \right\|_F} \le {c_{\mathit{\boldsymbol{\hat \zeta }}\max }} + {\left\| {{\mathit{\boldsymbol{\zeta }}^ * }} \right\|_F}, $ | (45) |
| $ \left\| {\mathit{\boldsymbol{x}}\left( t \right)} \right\| \le {c_{x\max }} + \mathop {\max }\limits_{i \in \left[ {0,t} \right]} \left\{ {{{\left\| {\mathit{\boldsymbol{x}}\left( \tau \right)} \right\|}_F}} \right\}. $ | (46) |
结论2 系统的状态及控制器权值指数收敛于一个有界紧集Ωs内.
| $ \left\{ \begin{array}{l} {\mathit{\Omega }_s} = \left\{ {\mathit{\boldsymbol{x}},\boldsymbol{\tilde \vartheta} ,\tilde \zeta \left| {\mathop {\lim }\limits_{t \to \infty } \left\| {\mathit{\boldsymbol{e}}\left( t \right)} \right\| = \mu _e^ * } \right.,} \right.\\ \left. {\mathop {\lim }\limits_{t \to \infty } {{\left\| {\boldsymbol{\tilde \vartheta} } \right\|}_F} = \mu _\vartheta ^ * ,\mathop {\lim }\limits_{t \to \infty } {{\left\| {\mathit{\boldsymbol{\tilde \zeta }}} \right\|}_F} = \mathit{\boldsymbol{\mu }}_\zeta ^ * } \right\}. \end{array} \right. $ | (47) |
式中:e(t)=[z1T, z2T]T,xd(t)=[x1dT, x2dT]T,cxmax=
对结论1证明如下:
对式(43)两边从[0, t]积分可得
| $ 0 \le V\left( t \right) \le \left[ {V\left( 0 \right) - \tau /\rho } \right]{{\rm{e}}^{ - \rho t}} + \tau /\rho . $ | (48) |
即
| $ 0 \le V\left( t \right) \le V\left( 0 \right) + \tau /\rho $ |
根据上式和式(38)可得
| $ {\left\| {\boldsymbol{\tilde \vartheta} } \right\|_F} \le \sqrt {2{\lambda _1}V\left( t \right)} \le {c_{\tilde \vartheta \max }} $ |
| $ {\left\| {\mathit{\boldsymbol{\tilde \zeta }}} \right\|_F} \le \sqrt {2{\lambda _2}V\left( t \right)} \le {c_{\mathit{\boldsymbol{\tilde \zeta }}\max }}. $ |
由于
| $ {\left\| {\boldsymbol{\tilde \vartheta} } \right\|_F} - {\left\| {{\boldsymbol{\vartheta} ^ * }} \right\|_F} \le {\left\| {\boldsymbol{\hat \vartheta} - {\boldsymbol{\vartheta} ^ * }} \right\|_F} \le {c_{\vartheta \max }}, $ | (49) |
| $ {\left\| {\mathit{\boldsymbol{\hat \zeta }}} \right\|_F} - {\left\| {{\mathit{\boldsymbol{\zeta }}^ * }} \right\|_F} \le {\left\| {\mathit{\boldsymbol{\hat \zeta }} - {\mathit{\boldsymbol{\zeta }}^ * }} \right\|_F} \le {c_{\zeta \max }}. $ | (50) |
由于z1, z2, x1d有界,又因为e(t)=x1(t)-xd(t),可得
| $ \left\| {\mathit{\boldsymbol{x}}\left( t \right)} \right\| - \left\| {{\mathit{\boldsymbol{x}}_d}\left( t \right)} \right\| \le \left\| {\mathit{\boldsymbol{x}}\left( t \right) - {\mathit{\boldsymbol{x}}_d}\left( t \right)} \right\| \le {c_{\zeta \max }}. $ | (51) |
即式(46)成立,结论1得证.
对结论2证明如下.
由式(49)可得
| $ \left\| {e\left( t \right)} \right\| \le \sqrt {2\left( {V\left( 0 \right) - \tau /\rho } \right){{\rm{e}}^{ - \rho t}} + 2\tau /\rho } , $ | (52) |
| $ {\left\| {\tilde \vartheta } \right\|_F} \le \sqrt {2{\lambda _1}\left( {V\left( 0 \right) - \tau /\rho } \right){{\rm{e}}^{ - \rho t}} + 2\tau /\rho } , $ | (53) |
| $ {\left\| {\tilde \zeta } \right\|_F} \le \sqrt {2{\lambda _2}\left( {V\left( 0 \right) - \tau /\rho } \right){{\rm{e}}^{ - \rho t}} + 2\tau /\rho } . $ | (54) |
若V(0)=τ/ρ,则0≤∀t,‖e(t)‖≤μe*.若V(0)≠τ/ρ,则存在Tr,使得当t>Tr时‖e(t)‖≤μe*.
令
| $ \mathop {\lim }\limits_{t \to \infty } \left\| {\mathit{\boldsymbol{e}}\left( t \right)} \right\| = \mu _e^ * , $ | (55) |
| $ \mathop {\lim }\limits_{t \to \infty } {\left\| {\boldsymbol{\tilde \vartheta} \left( t \right)} \right\|_F} = \mu _{\tilde \vartheta }^ * , $ | (56) |
| $ \mathop {\lim }\limits_{t \to \infty } {\left\| {\boldsymbol{\tilde \zeta} \left( t \right)} \right\|_F} = \boldsymbol{\mu }_{\tilde \zeta }^ * . $ | (57) |
结论2得证.由式(47)可知,通过调整k10, k20, λ1, αi, λ2, βi的大小,可以调整系统的收敛速度和收敛域的大小.
7 仿真与飞行验证 7.1 仿真验证为了验证控制器的鲁棒性,在仿真中,对气动系数进行拉偏设置:ΔCβL偏移15%,ΔCβN偏移-10%,CpL偏移20%,CrN偏移20%.
螺旋等速下降在降低飞行高度保持飞行速度不变.该机动不仅要求无人机具有较好的航向稳定性,协调转弯能力,航迹跟踪能力,还增加了油门量控制对无人机动能的保持.仿真结果如图 5所示.
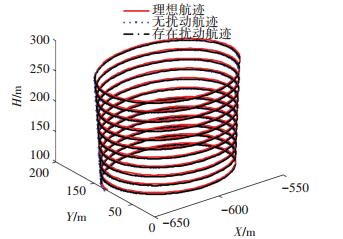
|
图 5 无人机等速螺旋下降 Figure 5 Trajectory of UAV spiral isokinetic drop maneuver |
从仿真图可知:无人机在等速螺旋下降机动过程中以相等速度高度从250 m降到了100 m.偏航角保持良好,无人机无侧滑现象.无人机可以很好地跟踪航迹,有/无扰动情况下的对比可知,在扰动存在的情况下,无人机能够跟踪飞行指令,系统具有对扰动较好的适应能力.
7.2 飞行验证从上面的控制律设计可知,控制的目的是跟踪α, β, φ.但是,由于机载设备不能直接测量迎角、侧滑角信号.因此,这里采用加速度计信号和GPS速度信号合成所需要的气流角的形式.其表达式为
| $ \dot \alpha = \frac{{u\dot {w - \dot wu}}}{{{u^2} + {w^2}}},\dot \beta = \frac{{\dot {vV - v\dot V}}}{{{V^2}\cos \beta }}. $ |
通过以上两式,可以得到控制器需要的反馈信号.
无人机一个连续机动为在殷麦曼(Immelmann maneuver)机动之后紧接着作了一个莱维斯曼(Ranversman)机动.飞翼无人机大迎角机动的航点和跟踪航迹如下图 6所示.飞翼无人机大迎角机动姿态如下图 7所示.
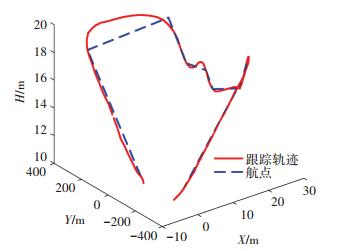
|
图 6 飞翼无人机的航迹 Figure 6 The trajectory of Fly-wing UAV |
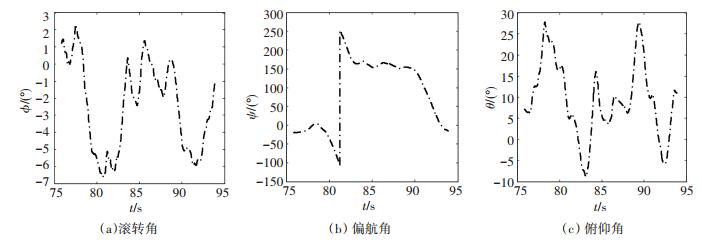
|
图 7 飞翼无人机的姿态图 Figure 7 The attitude of fly-wing UAV |
从图 6可以看出,无人机由平飞模态进行爬升同时改变机头指向.在高度最大时,无人机开始俯冲,速度增大并建立新的平飞模态.当新的模态建立后无人机立即进行跃升转弯并将机头指向改变180°.无人机的能量快速从动能转化为了势能,并且实现了机头指向的转换.从姿态图 7可知,无人机的转弯过程是协调的.从飞行结果可以看出,无人机可以很好地完成机动动作.整个飞行过程中,无人机姿态稳定,飞行状态良好.证明本文设计的控制器是有效的.
8 结论1) 同传统反步控制方法相比,控制器增加了内环解耦结构,并在解耦的前段增加了气动补偿模块.
2) 该气动补偿模块消除了飞行过程中的气动耦合和惯性耦合项,却在控制结构中保留气动阻尼项,使得线性化后的系统为弱非线性系统.
3) 在此基础上,设计了理论严谨的利于李导数的微分几何解耦方法,消除了运动耦合项.
| [1] |
LAN C E, LI J, YAU W, et al. Longitudinal and lateral-directional coupling effects on nonlinear unsteady aerodynamic modeling from flight data[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit. Washington DC: AIAA, 2013:394-402.
http://arc.aiaa.org/doi/abs/10.2514/6.2002-4804
|
| [2] |
ALIKHAN M, PEYADA N K, GO T H. Flight dynamics and optimization of three-dimensional perching maneuver[J].
Journal of Guidance Control Dynamics, 2015, 36(6): 1791-1797.
|
| [3] |
GUO Y, YAO Y, WANG S, et al. Maneuver control strategies to maximize prediction errors in ballistic middle phase[J].
Journal of Guidance Control & Dynamics, 2013, 36(4): 1225-1234.
|
| [4] |
ZHI Q, CAI Y L. Energy-management steering maneuver for thrust vector-controlled interceptors[J].
Journal of Guidance Control & Dynamics, 2012, 35(6).
|
| [5] |
MUELLER J B, GRIESEMER P R, THOMAS S J. Avoidance maneuver planning incorporating station-keeping constraints and automaticpelaxation[J].
Journal of Aerospace Computing Information & Communication, 2013, 10(6): 306-322.
|
| [6] |
王猛杰, 额日其太, 王强, 等. 激波矢量控制喷管落压比影响矢量性能及分离区控制数值模拟[J].
航空动力学报, 2015, 30(3): 527-538.
WAND Mengjie, Eriqitai, WAND Qiang. Numerical simulaton of nozzle pressure ratio effect on vector performance and separation control for shock vector control nozzle[J]. Journal of Aerospace Power, 2015, 30(3): 527-538. |
| [7] |
KIRANYAZ S, INCE T, GABBOUJ M. Dynamic data clustering using stochastic approximation driven multi-dimensionalparticle swarm optimization[J].
Lecture Notes in Computer Science, 2010, 22(10): 1448-1462.
|
| [8] |
ANEELY F G J Y. Performance studies of shock vector control fluidic thrust Vectoring[C]//43rd Joint Propulsion Conference. Washington DC:AIAA, 2007.
https://arc.aiaa.org/doi/abs/10.2514/6.2007-5086
|
| [9] |
DEERE K A. Summary of fluidic thrust vectoring research conducted at NASA langley research center[J].
Aiaa Journal, 2003, 23(26): 1-18.
|
| [10] |
SADIQ M U. Performance analysis and flowfield characterization of secondary injection thrust vector control (SITVC) for a 2DCD nozzle[J].
Dissertations & Theses-Gradworks, 2007, 534(1): 85-108.
|
| [11] |
YANG Y, CHEN X, LI C. Transient performance improvement in model reference adaptive control using H∞ math container loading mathjax, optimal method[J].
Journal of the Franklin Institute, 2015, 352(1): 16-32.
DOI: 10.1016/j.jfranklin.2014.09.014 |
| [12] |
杨艺, 陈欣, 李春涛. 一种可保证瞬态特性的改进鲁棒模型参考自适应控制[J].
控制与决策, 2015, 43(8): 1379-1385.
YANG Yi, CHIN Xi, LI Chuntao. An improved robust model reference adaptive control for transient stability[J]. Control and Decision, 2015, 43(8): 1379-1385. |
| [13] |
朱纪洪, 张尚敏, 周池军, 等. 飞机超机动状态动力学特征及对控制系统的挑战[J].
控制理论与应用, 2014, 31(12): 1650-1662.
ZHU Jihong, ZHANG Shangmin, ZHOU Chijun, et al. Dynamic characteristics and challenges for control system of super-maneuverable aircraft[J]. Control Theory & Applications, 2014, 31(12): 1650-1662. |
| [14] |
WILSON J R. UAV worldwide roundup 2007[J].
Aerospace America, 2007, 45(5): 30-37.
|
| [15] |
JIRASEKA, CUMMINGS R M, SCHUETTE A, et al. The NATO STO AVT-201 task group on extended assessment of stability an control prediction methods for NATO air vehicles: summary, conclusions and lessons learned[C]//Aiaa Applied Aerodynamics Conference. : AIAA, 2014:1250-1253.
http://arc.aiaa.org/doi/abs/10.2514/6.2014-2394
|
| [16] |
李继广, 陈欣, 王鑫, 等. 飞翼无人机机动飞行非线性鲁棒自适应控制[J].
系统工程与电子技术, 2017, 39(9): 2058-2068.
LI Jiguang, CHEN Xin, WANG Xin, et al. Flying wing UAV maneuvering flight nonlinear robust adaptive control[J]. Systems Engineering and Electronics, 2017, 39(9): 2058-2068. DOI: 10.3969/j.issn.1001-506X.2017.09.20 |
| [17] |
李继广, 陈欣, 李亚娟, 张榕. 飞翼无人机机动飞行非线性鲁棒控制方法. 北京航空航天大学学报. (2017-05-31)2017-07-25]. http://kns.cnki.net/kcms/detail/11.2625.V.20170531.1028.002.html. DOI: 10.13700/j.bh.1001-5965.2017.0014.
LI Jiguang, CHEN Xin, LI Yajuan. Control system design study of nonlinear robust method on flying wing UAV. Journal of Beijing University of Aeronautics and Astronautics.(2017-05-31). http://kns.cnki.net/kcms/detail/11.2625.V.20170531.1028.002.html.DOI:10.13700/j.bh.1001-5965.2017.0014. |
| [18] |
LI J G, CHEN X, LI Y, et al. Control system design of flying-wing UAV based on nonlinear methodology[J].
Defence Technology, 2017.
|
| [19] |
SOEST W R V, CHU Q P, MULDER J A. Combined feedback linearization and constrained model predictive control for entry flight[J].
Journal of Guidance Control Dynamics, 2012, 29(2): 427-434.
|
| [20] |
SONNEVELDT L, CHU Q P, MULDER J A. Nonlinear flight control design using constrained adaptive backstepping[J].
Journal of Guidance Control & Dynamics, 2012, 30(2): 322-336.
|
| [21] |
LEE T, KIM Y. Nonlinear adaptive flight control using backstepping and neural networks controller[J].
Journal of Guidance Control & Dynamics, 2012, 24(4): 675-682.
|
| [22] |
SIEBERLING S, CHU Q P, MULDER J A. Robust flight control using incremental nonlinear dynamic inversion and angular acceleration prediction[J].
Journal of Guidance Control & Dynamics, 2010, 33(6): 1732-1742.
|
| [23] |
MACKUNIS W, PATRE P M, KAISER M K, et al. Asymptotic tracking for aircraft via robust and adaptive dynamic inversion methods[J].
IEEE Transactions on Control Systems Technology, 2010, 18(6): 1448-1456.
DOI: 10.1109/TCST.2009.2039572 |
| [24] |
JOHNSON E N, TURBE M A. Modeling, control, and flight testing of a small-ducted fan aircraft[J].
Journal of Guidance Control & Dynamics, 2006, 29(4): 769-779.
|
| [25] |
XU B, HUANG X, WANG D, et al. Dynamic surface control of constrained hypersonic flight models with parameter estimation and actuator compensation[J].
Asian Journal of Control, 2014, 16(1): 162-174.
DOI: 10.1002/asjc.2014.16.issue-1 |
 2017, Vol. 49
2017, Vol. 49


