2. 北京航天自动控制研究所,北京 100854
2. Beijing Aerospace Automatic Control Institute, Beijing 100854, China
水下自主航行器(AUV)是一种非常重要的海洋开发工具.由于其强大的自主能力,AUV可以完成人类所安排的各种任务,并被广泛的应用到军事以及科研当中[1].当AUV在近水面航行时,垂直面的运动控制是其主要的研究方向之一,然而AUV系统的非线性特点以及近水面剧烈的海浪干扰,使研究的难度大大提升.目前国内外已经有了很深入的研究成果, 文献[2]提出了Backstepping技术以及快速积分终端滑模控制器来分别对航速和深度进行控制,然而其中并没有考虑两种控制器之间的耦合作用.文献[3]设计了改进的动态滑模控制器,较好地提高了深度跟踪控制的性能;文献[4]基于解析滑模控制器的方法获得了时间最优的轨迹跟踪;文献[5]提出了一种基于傅里叶系数展开及伪波普的非线性动态控制器,以实现深度跟踪的目的;文献[6]研究了模糊反馈线性化方法,在去掉了两种一般假设条件的情况下对深度运动的非线性动态进行控制,然而文中并没有考虑离散时间模型,且缺少足够的仿真验证;文献[7]考虑了重力和浮力变化对深度跟踪稳态误差的影响,通过在外环增加了开关PI控制器消除了稳态误差;文献[8]通过静态输出反馈控制器来完成下潜任务,然而所用的仍然是线性模型.
本文针对近水面海浪干扰下的AUV垂直面运动非线性模型,设计了一种降维状态观测器来进行AUV的状态估计,并将估计状态用于所设计的预测控制器及其预测模型在线线性化的过程当中,有效地实现了AUV深度跟踪和俯仰姿态控制.
1 AUV垂直面运动离散化模型首先假设AUV以恒定速度uc航行于近水面,重力与浮力近似相等,且重心与浮心在同一纵向轴线上,并忽略横摇,横荡和艏摇的影响,并假设小纵摇角θ[7],且二阶以上的水动力系数可以忽略.
由于数字控制器是通过零阶保持器来实现,因此可以通过对现有AUV连续状态方程进行欧拉变换[9],来得到所需的AUV非线性模型的离散形式为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{Ax}}\left( k \right) + \mathit{\boldsymbol{g}}\left( {k,\mathit{\boldsymbol{x}}\left( k \right)} \right) + \mathit{\boldsymbol{Bu}}\left( k \right) + \mathit{\boldsymbol{Dw}}\left( k \right),\\ \mathit{\boldsymbol{y}}\left( k \right) = \mathit{\boldsymbol{Cx}}\left( k \right). \end{array} \right. $ | (1) |
式中:x(k)=[ω, q, z, θ]T∈Rn,ω为垂荡速度,q为纵摇角速度,z为航行深度,θ为纵摇角,A=(TsAc+I),B=TsBc,D=TsDc,Ts为采样周期,w(k)为海浪扰动,u(k)∈Rm为输入,y(k)∈Rp为输出,g(k, x(k))=Tsgc(t, x(t))为非线性项. Ac,Bc,Dc,gc(t, x(t))均来自AUV连续状态方程,由AUV动力学与运动学方程[10]转化得出.
本文中为便于理论的推导,可设m=2,p=2,n=4,d=2,C为行满秩,且rank(C)=2,并假设(A, C)可观测,g(k, x(k))满足Lipschitz条件[11].
2 基于降维观测器的预测控制本文所提出的基于降维观测器的预测控制方法,其中ROSO部分独立于预测控制器,并可以保证预测控制器所需状态估计精度,其总体结构如图 1所示.

|
图 1 系统结构框图 Figure 1 Block diagram of system |
首先,为保证系统在未知扰动下的能观性,需要假设rank(CD)=rank(D),即ROSO存在的必要性条件.由文献[12]可知,(A, C)可观测是全维状态观测器(FOSO)存在的必要性条件.在文献[13]中,ROSO设计所用到的非奇异坐标变换不会改变系统的能观性,因此不难证明,上述两种观测器的存在性条件是等价的,也就是说ROSO与FOSO的应用范围是相同的.
由于C是行满秩,那么一定存在C的标准正交基使
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{z}}_1}\left( {k + 1} \right)}\\ {{\mathit{\boldsymbol{z}}_2}\left( {k + 1} \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{11}}}&{{\mathit{\boldsymbol{A}}_{12}}}\\ {{\mathit{\boldsymbol{A}}_{21}}}&{{\mathit{\boldsymbol{A}}_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{z}}_1}\left( k \right)}\\ {{\mathit{\boldsymbol{z}}_2}\left( k \right)} \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}^ \bot }}\\ \mathit{\boldsymbol{C}} \end{array}} \right]\mathit{\boldsymbol{g}}\left( {k,{\mathit{\boldsymbol{T}}^{ - 1}}\mathit{\boldsymbol{z}}\left( k \right)} \right) + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}}\\ {{\mathit{\boldsymbol{B}}_2}} \end{array}} \right]\mathit{\boldsymbol{u}}\left( k \right) + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{D}}_1}}\\ {{\mathit{\boldsymbol{D}}_2}} \end{array}} \right]\mathit{\boldsymbol{w}}\left( k \right),}\\ {\mathit{\boldsymbol{y}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{{\bf{0}}_{p \times \left( {n - p} \right)}}}&{{\mathit{\boldsymbol{I}}_p}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{z}}_1}\left( k \right)}\\ {{\mathit{\boldsymbol{z}}_2}\left( k \right)} \end{array}} \right].} \end{array} $ |
令μ(k)=A12y(k)+B1u(k),ρ(k)=y(k+1)-A22y(k)-B2u(k).可得到ROSO结构为
| $ \begin{array}{l} {{\mathit{\boldsymbol{\hat z}}}_1}\left( {k + 1} \right) = {\mathit{\boldsymbol{A}}_{11}}{{\mathit{\boldsymbol{\hat z}}}_1}\left( k \right) + {\mathit{\boldsymbol{C}}^ \bot }\mathit{\boldsymbol{g}}\left( {k,{\mathit{\boldsymbol{T}}^{ - 1}}\mathit{\boldsymbol{\hat z}}\left( k \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{\mu }}\left( k \right) - \mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{\hat \rho }}\left( k \right) - \mathit{\boldsymbol{\rho }}\left( k \right)} \right), \end{array} $ | (2) |
| $ \mathit{\boldsymbol{\hat \rho }}\left( k \right) = {\mathit{\boldsymbol{A}}_{21}}{{\mathit{\boldsymbol{\hat z}}}_1}\left( k \right) + \mathit{\boldsymbol{Cg}}\left( {k,{\mathit{\boldsymbol{T}}^{ - 1}}\mathit{\boldsymbol{\hat z}}\left( k \right)} \right). $ | (3) |
式中:
设e(k)=
| $ \begin{array}{l} \mathit{\boldsymbol{e}}\left( {k + 1} \right) = \left( {{{\mathit{\boldsymbol{\bar A}}}_1} - \mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\bar A}}}_2}} \right)\mathit{\boldsymbol{e}}\left( k \right) + \left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}_2} - {\mathit{\boldsymbol{C}}_1}} \right)\mathit{\boldsymbol{G}}\left( k \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{D}}_2} - {\mathit{\boldsymbol{D}}_1}} \right)\mathit{\boldsymbol{w}}\left( k \right). \end{array} $ | (4) |
式中:A1=A11,A2=A21,C1=-C⊥,C2=-C.
通过状态估计误差(4)可以看出,ROSO的维数(n-p)小于FOSO[14]的维数(n),也就是说,干扰w(k)到状态误差e(k)之间的传递函数通过降低观测器的维数得以简化,与FOSO相比,ROSO的系统结构更为简单.
下面用一个定理来给出具有约束条件的ROSO设计,其中ROSO的状态估计性能可以通过一个H∞性能指标来指定.
定理1 对于给定标量γ1>0,若存在对称正定矩阵P∈R(n-p)×(n-p),标量ε1>0以及矩阵Y∈R(n-p)×p使得如下条件成立:
| $ \left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{\bar P}}}&{\mathit{\boldsymbol{\bar P}}{{\mathit{\boldsymbol{\bar A}}}_1} - \mathit{\boldsymbol{\bar Y}}{{\mathit{\boldsymbol{\bar A}}}_2}}&{\mathit{\boldsymbol{\bar Y}}{\mathit{\boldsymbol{C}}_2} - \mathit{\boldsymbol{\bar P}}{\mathit{\boldsymbol{C}}_1}}&{\mathit{\boldsymbol{\bar Y}}{\mathit{\boldsymbol{D}}_2} - \mathit{\boldsymbol{\bar P}}{\mathit{\boldsymbol{D}}_1}}&{\bf{0}}\\ * &{ - \mathit{\boldsymbol{\bar P}} + {\varepsilon _1}L_g^2{\mathit{\boldsymbol{I}}_{n - p}}}&{\bf{0}}&{\bf{0}}&{{\mathit{\boldsymbol{I}}_{n - p}}}\\ *&* &{ - {\varepsilon _1}{\lambda _{\min }}\left( {{\mathit{\boldsymbol{T}}^{\rm{T}}}\mathit{\boldsymbol{T}}} \right){\mathit{\boldsymbol{I}}_n}}&{\bf{0}}&{\bf{0}}\\ *&*&* &{ - {\gamma _1}{\mathit{\boldsymbol{I}}_d}}&{\bf{0}}\\ *&*&*&* &{ - {\gamma _1}{\mathit{\boldsymbol{I}}_{n - p}}} \end{array}} \right] \le 0. $ | (5) |
式中:Y=PG,*表示矩阵中对称的元素,Lg为Lipschitz常数[11],那么状态误差(4)就满足H∞性能指标‖e(k)‖2≤γ1‖w(k)‖2,且ROSO增益矩阵可以表示为G=P-1Y.
证明 选择如下李雅普诺夫函数
| $ \mathit{\boldsymbol{V}}\left( k \right) = {\mathit{\boldsymbol{e}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{\bar Pe}}\left( k \right), $ | (6) |
那么
| $ \Delta \mathit{\boldsymbol{V}}\left( k \right) = \mathit{\boldsymbol{V}}\left( {k + 1} \right) - \mathit{\boldsymbol{V}}\left( k \right). $ | (7) |
定义一个H∞性能指标为
| $ {\mathit{J}_1} = \sum\limits_{k = 0}^K {\left[ {\frac{1}{{{\gamma _1}}}{\mathit{\boldsymbol{e}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{e}}\left( k \right) - {\gamma _1}{\mathit{\boldsymbol{w}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{w}}\left( k \right)} \right]} . $ |
在零初始条件下
| $ {\mathit{J}_1} \le \sum\limits_{k = 0}^K {\left[ {\frac{1}{{{\gamma _1}}}{\mathit{\boldsymbol{e}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{e}}\left( k \right) - {\gamma _1}{\mathit{\boldsymbol{w}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{w}}\left( k \right) + \Delta \mathit{\boldsymbol{V}}\left( k \right)} \right]} . $ | (8) |
由g(k, x(k))满足Lipschitz条件,且
| $ \mathit{\boldsymbol{\hat x}}\left( k \right) - \mathit{\boldsymbol{x}}\left( k \right) = {\mathit{\boldsymbol{T}}^{ - 1}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{e}}\left( k \right)}\\ {\bf{0}} \end{array}} \right], $ | (9) |
可得
| $ {\varepsilon _1}{\mathit{\boldsymbol{G}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{G}}\left( k \right) \le {\varepsilon _1}L_g^2\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}^{\rm{T}}}\left( k \right)}&{\bf{0}} \end{array}} \right]{\left( {{\mathit{\boldsymbol{T}}^{ - 1}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{T}}^{ - 1}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{e}}\left( k \right)}\\ {\bf{0}} \end{array}} \right]. $ |
等式两边同时乘以λmin(TTT)得到如下不等式
| $ {\varepsilon _1}L_g^2{\mathit{\boldsymbol{e}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{e}}\left( k \right) - {\varepsilon _1}{\mathit{\boldsymbol{\lambda }}_{\min }}\left( {{\mathit{\boldsymbol{T}}^{\rm{T}}}\mathit{\boldsymbol{T}}} \right){\mathit{\boldsymbol{G}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{G}}\left( k \right) \ge 0. $ | (10) |
式中λmin(·)为最小特征矩阵.
那么将式(7)、(10)代入式(8), 可得
| $ {J_1} \le \sum\limits_{k = 0}^K {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}^{\rm{T}}}\left( k \right)}&{{\mathit{\boldsymbol{G}}^{\rm{T}}}\left( k \right)}&{{\mathit{\boldsymbol{w}}^{\rm{T}}}\left( k \right)} \end{array}} \right]\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{e}}\left( k \right)}\\ {\mathit{\boldsymbol{G}}\left( k \right)}\\ {\mathit{\boldsymbol{w}}\left( k \right)} \end{array}} \right]} . $ |
式中:
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega} = }}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{c}}_{11}}}&{{{\left( {{{\mathit{\boldsymbol{\bar A}}}_1} - \mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\bar A}}}_2}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\bar P}}\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}_2} - {\mathit{\boldsymbol{C}}_1}} \right)}&{{{\left( {{{\mathit{\boldsymbol{\bar A}}}_1} - \mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\bar A}}}_2}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\bar P}}\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{D}}_2} - {\mathit{\boldsymbol{D}}_1}} \right)}\\ * &{{\mathit{\boldsymbol{c}}_{22}}}&{{{\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}_2} - {\mathit{\boldsymbol{C}}_1}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\bar P}}\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{D}}_2} - {\mathit{\boldsymbol{D}}_1}} \right)}\\ *&* &{{\mathit{\boldsymbol{c}}_{33}}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{c}}_{11}} = {\left( {{{\mathit{\boldsymbol{\bar A}}}_1} - \mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\bar A}}}_2}} \right)^{\rm{T}}}\mathit{\boldsymbol{\bar P}}\left( {{{\mathit{\boldsymbol{\bar A}}}_1} - \mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\bar A}}}_2}} \right) - \mathit{\boldsymbol{\bar P}} + \left( {{\varepsilon _1}L_g^2 + \frac{1}{{{\gamma _1}}}} \right){\mathit{\boldsymbol{I}}_{n - p}}, $ |
| $ {\mathit{\boldsymbol{c}}_{22}} = {\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}_2} - {\mathit{\boldsymbol{C}}_1}} \right)^{\rm{T}}}\mathit{\boldsymbol{\bar P}}\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}_2} - {\mathit{\boldsymbol{C}}_1}} \right) - {\varepsilon _1}{\lambda _{\min }}\left( {{\mathit{\boldsymbol{T}}^{\rm{T}}}\mathit{\boldsymbol{T}}} \right){\mathit{\boldsymbol{I}}_n}, $ |
| $ {\mathit{\boldsymbol{c}}_{33}} = {\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{D}}_2} - {\mathit{\boldsymbol{D}}_1}} \right)^{\rm{T}}}\mathit{\boldsymbol{\bar P}}\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{D}}_2} - {\mathit{\boldsymbol{D}}_1}} \right) - {\gamma _1}{\mathit{\boldsymbol{I}}_d}. $ |
通过应用Schur补充引理可得Ω<0的等价条件为
| $\small{ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{c}}_{11}} - \frac{1}{{{\gamma _1}}}{\mathit{\boldsymbol{I}}_{n - p}}}&{{{\left( {{{\mathit{\boldsymbol{\bar A}}}_1} - \mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\bar A}}}_2}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\bar P}}\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}_2} - {\mathit{\boldsymbol{C}}_1}} \right)}&{{{\left( {{{\mathit{\boldsymbol{\bar A}}}_1} - \mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\bar A}}}_2}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\bar P}}\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{D}}_2} - {\mathit{\boldsymbol{D}}_1}} \right)}&{{\mathit{\boldsymbol{I}}_{n - p}}}\\ * &{{\mathit{\boldsymbol{c}}_{22}}}&{{{\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}_2} - {\mathit{\boldsymbol{C}}_1}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\bar P}}\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{D}}_2} - {\mathit{\boldsymbol{D}}_1}} \right)}&{\bf{0}}\\ *&* &{{\mathit{\boldsymbol{c}}_{33}}}&{\bf{0}}\\ *&*&* &{ - {\gamma _1}{\mathit{\boldsymbol{I}}_{n - p}}} \end{array}} \right] \le 0.} $ | (11) |
将式(11)表示为
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{{\left( {{{\mathit{\boldsymbol{\bar A}}}_1} - \mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\bar A}}}_2}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\bar P}}}\\ {{{\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}_2} - {\mathit{\boldsymbol{C}}_1}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\bar P}}}\\ {{{\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{D}}_2} - {\mathit{\boldsymbol{D}}_1}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\bar P}}}\\ {\bf{0}} \end{array}} \right]{{\mathit{\boldsymbol{\bar P}}}^{ - 1}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\bar P}}\left( {{{\mathit{\boldsymbol{\bar A}}}_1} - \mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\bar A}}}_2}} \right)}&{\mathit{\boldsymbol{\bar P}}\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}_2} - {\mathit{\boldsymbol{C}}_1}} \right)}&{\mathit{\boldsymbol{\bar P}}\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{D}}_2} - {\mathit{\boldsymbol{D}}_1}} \right)}&{\bf{0}} \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{\bar P}} + {\varepsilon _1}L_g^2{\mathit{\boldsymbol{I}}_{n - p}}}&{\bf{0}}&{\bf{0}}&{{\mathit{\boldsymbol{I}}_{n - p}}}\\ * &{ - {\varepsilon _1}{\lambda _{\min }}\left( {{\mathit{\boldsymbol{T}}^{\rm{T}}}\mathit{\boldsymbol{T}}} \right){\mathit{\boldsymbol{I}}_n}}&{\bf{0}}&{\bf{0}}\\ *&* &{ - {\gamma _1}{\mathit{\boldsymbol{I}}_d}}&{\bf{0}}\\ *&*&* &{ - {\gamma _1}{\mathit{\boldsymbol{I}}_{n - p}}} \end{array}} \right] \le 0,} \end{array} $ |
并再次应用Schur补充引理,最后可证明定理中式(5)成立,保证了‖e(k)‖2≤γ1‖w(k)‖2,进而证明状态误差(4)呈指数收敛.与FOSO相比,本文通过引入约束条件(5)来对干扰w(k)进行抑制,减小了w(k)对状态误差(4)的影响.
在实际应用中,为了消去ρ(k)中的y(k+1),下面定义一个新的变量χ(k)=
| $ \begin{array}{l} \mathit{\boldsymbol{\chi }}\left( {k + 1} \right) = \left( {{{\mathit{\boldsymbol{\bar A}}}_1} - \mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\bar A}}}_2}} \right)\mathit{\boldsymbol{\chi }}\left( k \right) + \left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}_2} - } \right.\\ \;\;\;\left. {{\mathit{\boldsymbol{C}}_1}} \right)\mathit{\boldsymbol{g}}\left( {k,{\mathit{\boldsymbol{T}}^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat z}}}_1}\left( k \right)}\\ {\mathit{\boldsymbol{y}}\left( k \right)} \end{array}} \right]} \right) + \left( {\left( {{{\mathit{\boldsymbol{\bar A}}}_1} - \mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\bar A}}}_2}} \right)} \right. + \\ \;\;\;\left. {\left( {{\mathit{\boldsymbol{I}}_{n - p}}{\mathit{\boldsymbol{A}}_{12}} - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{A}}_{22}}} \right)} \right)\mathit{\boldsymbol{y}}\left( k \right) + \left( {{\mathit{\boldsymbol{I}}_{n - p}}{\mathit{\boldsymbol{B}}_1} - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{B}}_2}} \right)\mathit{\boldsymbol{u}}\left( k \right). \end{array} $ |
最后,状态估计可以表示
| $ \mathit{\boldsymbol{\hat x}}\left( k \right) = {\mathit{\boldsymbol{T}}^{ - 1}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\chi }}\left( k \right) + \mathit{\boldsymbol{Gy}}\left( k \right)}\\ {\mathit{\boldsymbol{y}}\left( k \right)} \end{array}} \right]. $ | (12) |
本节首先简要的介绍了非线性预测控制(NPC)的原理,然后提出了一种将非线性模型在线线性化的方法,与NPC相比,模型在线线性化可以将非线性优化问题转化成为二次规划(QP)问题.
首先,在不加入扰动的情况下,将式(1)转化为具有线性输出的非线性状态空间模型的一般形式:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}\left( {k + 1} \right) = f\left( {\mathit{\boldsymbol{x}}\left( k \right),\mathit{\boldsymbol{u}}\left( k \right)} \right),}\\ {\mathit{\boldsymbol{y}}\left( k \right) = \mathit{\boldsymbol{Cx}}\left( k \right).} \end{array} $ |
式中非线性函数f:Rn+m→Rn.
那么NPC所用Np步的预测模型可表示为
| $ \mathit{\boldsymbol{\tilde y}}\left( {k + {N_p}} \right) = \mathit{\boldsymbol{C}}\left( {f\left( {\mathit{\boldsymbol{x}}\left( {k + {N_p} - 1\left| k \right.} \right),\mathit{\boldsymbol{u}}\left( {k + {N_p} - 1\left| k \right.} \right)} \right.} \right). $ |
将参考输出轨迹和预测输出向量表示为
| $ {\mathit{\boldsymbol{y}}_{{\rm{ref}}}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{y}}_{{\rm{ref}}}}\left( {k + 1\left| k \right.} \right)}\\ \vdots \\ {{\mathit{\boldsymbol{y}}_{{\rm{ref}}}}\left( {k + {N_p}\left| k \right.} \right)} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{\tilde y}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde y}}\left( {k + 1\left| k \right.} \right)}\\ \vdots \\ {\mathit{\boldsymbol{\tilde y}}\left( {k + {N_p}\left| k \right.} \right)} \end{array}} \right]. $ |
那么NPC的性能指标可表示为
| $ J = \left\| {{\mathit{\boldsymbol{y}}_{{\rm{ref}}}}\left( k \right) - \mathit{\boldsymbol{\tilde y}}\left( k \right)} \right\|_\mathit{\boldsymbol{R}}^2 + \left\| {\mathit{\boldsymbol{u}}\left( k \right)} \right\|_\mathit{\boldsymbol{Q}}^2. $ |
式中:R和Q为权重系数阵,u为控制增量向量.
一般NPC性能指标优化问题可以表示为
在求解上述非线性的非凸优化问题时,计算的耗时性和可行性都是现阶段存在的问题.序列二次规划[15](sequential quadratic programming,SQP)技术是求解此类问题最常用的方法. SQP作为牛顿法的扩展,经常被用于求解最优化问题中满足Kuhn-Tucker条件的收敛解[16]. SQP的实质即是在每个迭代过程中,通过构造并求解一个近似的QP子问题来产生一个新的未知向量值,例如第K次迭代的方向向量dKT=[dũT dyT],其作为迭代的搜索方向,使得最终结果向原非线性问题的解去收敛.
在第K次迭代中,求解QP问题
| $ \mathop {\min }\limits_\mathit{\boldsymbol{d}} \nabla J{\left( {{\mathit{\boldsymbol{W}}_K}} \right)^{\rm{T}}}\mathit{\boldsymbol{d}} + \frac{1}{2}{\mathit{\boldsymbol{d}}^{\rm{T}}}{\mathit{\boldsymbol{B}}_K}\mathit{\boldsymbol{d}}. $ |
且服从关于WK的线性化等式及不等式约束,式中BK为拉格朗日算子的Hessian矩阵.由此得到dK来进行下一次迭代WK+1=WK+dK.
由上述SQP过程可以看出,在采样时刻k所包含的多次迭代中,每一次迭代都要处理一个QP过程,然而在线性化预测控制中,每个采样时刻仅需要进行一次QP过程.因此本文针对上述问题提出了一种将非线性模型在线线性化的方法.
当前采样时刻的线性化模型为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{x}}\left( {k + 1} \right) = \left( {\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{\bar g}}\left( {x,k} \right)} \right)\mathit{\boldsymbol{x}}\left( k \right) + \mathit{\boldsymbol{Bu}}\left( k \right)\mathit{\boldsymbol{ + Dw}}\left( k \right),\\ \mathit{\boldsymbol{y}}\left( k \right) = \mathit{\boldsymbol{Cx}}\left( k \right). \end{array} \right. $ | (13) |
式中ḡ(x, k)为g(k, x(k))线性化后的结果,即
| $ \mathit{\boldsymbol{\bar g}}\left( {\mathit{\boldsymbol{x}},k} \right) = \frac{{\partial \mathit{\boldsymbol{g}}\left( {k,\mathit{\boldsymbol{x}}\left( k \right)} \right)}}{{\partial \mathit{\boldsymbol{x}}\left( k \right)}}\left| {_{\mathit{\boldsymbol{x}}\left( k \right) = \mathit{\boldsymbol{\hat x}}\left( k \right)}} \right.. $ | (14) |
式(14)结合了上一节中的状态估计信息,其中g(k, x(k))具体表示为如下形式
| $ \mathit{\boldsymbol{g}}\left( {k,\mathit{\boldsymbol{x}}\left( k \right)} \right) = \left[ {\begin{array}{*{20}{c}} {{g_{11}}{x_1}\left| {{x_1}} \right| + {g_{12}}{x_2}\left| {{x_2}} \right| + {g_{13}}{x_1}{x_2}}\\ {{g_{21}}{x_1}\left| {{x_1}} \right| + {g_{22}}{x_2}\left| {{x_2}} \right| + {g_{23}}{x_1}{x_2}}\\ 0\\ 0 \end{array}} \right], $ | (15) |
式中的非线性项系数可由前文提到的AUV动力学与运动学方程中的相应水动力系数计算得出.
将式(15)代入式(14)可得
| $ \mathit{\boldsymbol{\bar g}}\left( {x,k} \right) = \left[ {\begin{array}{*{20}{c}} {{{\bar g}_1}}&{{{\bar g}_2}}&0&0\\ {{{\bar g}_3}}&{{{\bar g}_4}}&0&0\\ 0&0&0&0\\ 0&0&0&0 \end{array}} \right], $ |
其中:
| $ {{\bar g}_1} = {g_{11}}\left| {{{\hat x}_1}} \right| + {g_{11}}{{\hat x}_1}{\mathop{\rm sgn}} \left( {{{\hat x}_1}} \right) + {g_{13}}{{\hat x}_2}, $ |
| $ {{\bar g}_2} = {g_{12}}\left| {{{\hat x}_2}} \right| + {g_{12}}{{\hat x}_2}{\mathop{\rm sgn}} \left( {{{\hat x}_2}} \right) + {g_{13}}{{\hat x}_1}, $ |
| $ {{\bar g}_3} = {g_{21}}\left| {{{\hat x}_1}} \right| + {g_{21}}{{\hat x}_1}{\mathop{\rm sgn}} \left( {{{\hat x}_1}} \right) + {g_{23}}{{\hat x}_2}, $ |
| $ {{\bar g}_4} = {g_{22}}\left| {{{\hat x}_2}} \right| + {g_{22}}{{\hat x}_2}{\mathop{\rm sgn}} \left( {{{\hat x}_2}} \right) + {g_{23}}{{\hat x}_1}. $ |
为推导过程简洁,定义Ā=A+ḡ(x, k-1),则k时刻未来Np步迭代的预测状态表示为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde x}}\left( {k + 1\left| k \right.} \right) = \mathit{\boldsymbol{\bar A\hat x}}\left( k \right) + \mathit{\boldsymbol{B\tilde u}}\left( {k\left| k \right.} \right) + \mathit{\boldsymbol{w}}\left( k \right),}\\ {\mathit{\boldsymbol{\tilde x}}\left( {k + 2\left| k \right.} \right) = \mathit{\boldsymbol{\bar A\hat x}}\left( {k + 1} \right) + \mathit{\boldsymbol{B\tilde u}}\left( {k + 1\left| k \right.} \right) + \mathit{\boldsymbol{w}}\left( k \right),}\\ \vdots \\ {\mathit{\boldsymbol{\tilde x}}\left( {k + {N_p}\left| k \right.} \right) = \mathit{\boldsymbol{\bar A\hat x}}\left( {k + {N_p} - 1} \right) + \mathit{\boldsymbol{B\tilde u}}\left( {k + {N_p} - 1\left| k \right.} \right) + \mathit{\boldsymbol{w}}\left( k \right).} \end{array} $ |
式中:ũ(k+p|k)为k时刻的预测输入,Np为预测时域.
在预测控制当中,增量预测模型是非常常见的一种形式,将ũ(k+i|k)=ũ(k+i-1)+Δũ(k+i|k)带入到上述预测状态中,并假设控制量只在小于控制时域Nu时会有作用,且Nu≤Np,同时假设w(k)在k时刻的预测值为0,因此可以用来预测未来动态的AUV垂直面运动预测模型为
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{ \boldsymbol{\varPsi} \hat x}}\left( k \right) + \mathit{\boldsymbol{ \boldsymbol{\varGamma} u}}\left( {k - 1} \right) + \mathit{\Theta }\mathit{\boldsymbol{u}}. $ | (16) |
其中:
| $ \mathit{\boldsymbol{y}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde y}}\left( {k + 1\left| k \right.} \right)}\\ \vdots \\ {\mathit{\boldsymbol{\tilde y}}\left( {k + {N_p}\left| k \right.} \right)} \end{array}} \right],\mathit{\boldsymbol{u}} = \left[ {\begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{\tilde u}}\left( {k\left| k \right.} \right)}\\ \vdots \\ {\Delta \mathit{\boldsymbol{\tilde u}}\left( {k + {N_u} - 1\left| k \right.} \right)} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{C\bar A}}}\\ {\mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{\bar A}}}^2}}\\ \vdots \\ {\mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{\bar A}}}^{{N_p}}}} \end{array}} \right],\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{CB}}}\\ {\mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{\bar AB}} + \mathit{\boldsymbol{B}}} \right)}\\ \vdots \\ {\sum\limits_{i = 0}^{{N_p} - 1} {\mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{\bar A}}}^i}\mathit{\boldsymbol{B}}} } \end{array}} \right], $ |
| $ \mathit{\boldsymbol{ \boldsymbol{\varTheta} = }}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{CB}}}& \cdots &{\bf{0}}\\ {\mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{\bar AB}} + \mathit{\boldsymbol{B}}} \right)}& \cdots &{\bf{0}}\\ \vdots&\ddots&\vdots \\ {\sum\limits_{i = 0}^{{N_p} - 1} {\mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{\bar A}}}^i}\mathit{\boldsymbol{B}}} }& \cdots &{\sum\limits_{i = 0}^{{N_p} - {N_u}} {\mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{\bar A}}}^i}\mathit{\boldsymbol{B}}} } \end{array}} \right]. $ |
对约束的处理能力是预测控制的优势之一,在AUV实际应用中,约束条件可以简要表示为
| $ {\mathit{\boldsymbol{\delta }}_{\min }} \le \mathit{\boldsymbol{\delta }} \le {\mathit{\boldsymbol{\delta }}_{\max }}, $ | (17) |
| $ \Delta {\mathit{\boldsymbol{\delta }}_{\min }} \le \Delta \mathit{\boldsymbol{\delta }} \le \Delta {\mathit{\boldsymbol{\delta }}_{\max }}, $ | (18) |
| $ {\mathit{\boldsymbol{y}}_{\min }} \le \mathit{\boldsymbol{y}} \le {\mathit{\boldsymbol{y}}_{\max }}. $ | (19) |
式中Δδ为AUV控制增量,即AUV升降舵的偏转角度,与式(16)中的u等价,式(17)~(19)可转化为如下矩阵不等式表达形式
| $ \mathit{\boldsymbol{M}}\Delta \mathit{\boldsymbol{\delta }} \le \mathit{\boldsymbol{\gamma }}. $ | (20) |
接下来将约束条件(20)加入到预测控制的性能指标当中,并简要表示为
| $ J = \frac{1}{2}{\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{Eu}} + {\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{F}} + {\mathit{\boldsymbol{f}}_0} + {\lambda ^{\rm{T}}}\left( {\mathit{\boldsymbol{Mu}} - \mathit{\boldsymbol{\gamma }}} \right). $ | (21) |
式中:
| $ \mathit{\boldsymbol{E}} = 2\left( {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}\mathit{\boldsymbol{Q \boldsymbol{\varTheta} + R}}} \right), $ |
| $ \mathit{\boldsymbol{F}} = 2{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} \hat x}}\left( k \right) + \mathit{\boldsymbol{ \boldsymbol{\varGamma} u}}\left( {k - 1} \right) - {\mathit{\boldsymbol{y}}_{{\rm{ref}}}}} \right), $ |
| $ \begin{array}{l} {\mathit{\boldsymbol{f}}_0} = {\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} \hat x}}\left( k \right) + \mathit{\boldsymbol{ \boldsymbol{\varGamma} u}}\left( {k - 1} \right) - {\mathit{\boldsymbol{y}}_{{\rm{ref}}}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} \hat x}}\left( k \right) + } \right.\\ \;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{ \boldsymbol{\varGamma} u}}\left( {k - 1} \right) - {\mathit{\boldsymbol{y}}_{{\rm{ref}}}}} \right). \end{array} $ |
通过求J关于u和λ的一阶偏导数,使其结果为零求得使J为最小值的u和λ的表达式为
| $ \mathit{\boldsymbol{\lambda }} = - {\left( {\mathit{\boldsymbol{M}}{\mathit{\boldsymbol{E}}^{ - 1}}{\mathit{\boldsymbol{M}}^{\rm{T}}}} \right)^{ - 1}}\left( {\mathit{\boldsymbol{\gamma }} + \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{E}}^{ - 1}}\mathit{\boldsymbol{F}}} \right), $ | (22) |
| $ \mathit{\boldsymbol{u}} = - {\mathit{\boldsymbol{E}}^{ - 1}}\left( {{\mathit{\boldsymbol{M}}^{\rm{T}}}\mathit{\boldsymbol{\lambda + F}}} \right) = \mathit{\boldsymbol{\eta }} - {\mathit{\boldsymbol{E}}^{ - 1}}{\mathit{\boldsymbol{M}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }}, $ | (23) |
式中η=-E-1F为不考虑约束的最优解.
然而不等式约束中往往含有无效约束,Kuhn-Tucker条件[15]也被用来定义关于λ的有效和无效约束条件.现有方法中,有效集法[16]是很常见的搜索有效约束的方法,其中把u作为决策变量.然而当一个多输入多输出系统含有非常多的约束条件时,计算量会变得非常大.这时,选择u的对偶变量λ作为决策变量可以简化QP的计算量,将式(23)代入到式(21)中得到新的预测控制性能指标为
| $ J = \frac{1}{2}{\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\mathit{\boldsymbol{H\lambda }} + {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}{\mathit{\boldsymbol{K}}_p} + \frac{1}{2}{\mathit{\boldsymbol{\gamma }}^{\rm{T}}}{\mathit{\boldsymbol{E}}^{ - 1}}\mathit{\boldsymbol{\gamma }}. $ | (24) |
式中:H=ME-1MT,Kp=γ+ME-1F,且服从新的约束条件λ≥0.
此时选用Hildreth QP方法[17]来解式(24)最小化的问题,这种QP方法属于逐个元素搜索,因而无需计算矩阵的逆,当有效集的个数大于u中元素的个数,或有效约束线性相关,那么迭代会在计数器最大值时终止,但是算法不会出错,只是结果会得到一个关于所违背的约束条件的近优解.最终得到收敛的λ*作为结果,计算出最优解为
| $ \mathit{\boldsymbol{u = \eta }} - {\mathit{\boldsymbol{E}}^{ - 1}}{\mathit{\boldsymbol{M}}^{\rm{T}}}{\mathit{\boldsymbol{\lambda }}^ * }. $ | (25) |
根据预测控制滚动优化的特点,每个采样周期优化计算的最后,将u中前m个元素Δu(k)用来更新预测控制的控制律u(k)=u(k-1)+Δu(k).
3 仿真实验在验证ROSO和预测控制器有效性的仿真实验中,本文采用DOLPHIN MARK Ⅱ型AUV,其具体的物理参数可见文献[10],其中非线性模型参数为
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {0.9600}&{0.0526}&0&{0.0002}\\ {0.0016}&{0.9597}&0&{ - 0.0127}\\ {0.1}&0&1&{ - 0.1852}\\ 0&{0.1}&0&1 \end{array}} \right], $ |
| $ \mathit{\boldsymbol{B = }}\left[ {\begin{array}{*{20}{c}} { - 0.0109}&{ - 0.0186}\\ { - 0.0092}&{0.0087}\\ 0&0\\ 0&0 \end{array}} \right], $ |
| $ \mathit{\boldsymbol{C = }}\left[ {\begin{array}{*{20}{c}} 0&0&1&0\\ 0&0&0&1 \end{array}} \right],\mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {0.0001}&0\\ 0&{0.0001}\\ {0.0001}&0\\ 0&{0.0001} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{g}}\left( {k,\mathit{\boldsymbol{x}}\left( k \right)} \right) = \left[ {\begin{array}{*{20}{c}} { - 0.0621{x_1}\left| {{x_1}} \right|}\\ {0.0002{x_1}\left| {{x_1}} \right| - 0.0003{x_2}\left| {{x_2}} \right|}\\ 0\\ 0 \end{array}} \right]. $ |
由rank(CD)=rank(D)=2,(A, C)可观,可以很容易验证ROSO的存在性.
通过施密特正交化可以得到非奇异矩阵T,其具体形式为一个四阶单位矩阵.
这里选择Lg=0.01作为Lipschitz常数,并结合Ā1,Ā2,C1,C2,D1,D2,借助MATLAB中的LMI工具箱,可以解得定理1中线性矩阵不等式的参数为
| $ \mathit{\boldsymbol{\bar P = }}\left[ {\begin{array}{*{20}{c}} {11.2513}&{ - 1.8117}\\ { - 1.8117}&{11.7637} \end{array}} \right],{\gamma _1} = 65.8062, $ |
| $ \mathit{\boldsymbol{\bar Y = }}\left[ {\begin{array}{*{20}{c}} {10.2026}&{0.3465}\\ { - 0.1909}&{10.0959} \end{array}} \right],{\varepsilon _1} = 108.4271. $ |
最后得到
| $ \mathit{\boldsymbol{\bar G = }}{{\mathit{\boldsymbol{\bar P}}}^{ - 1}}\mathit{\boldsymbol{\bar Y}} = \left[ {\begin{array}{*{20}{c}} {0.7880}&{1.2135}\\ {1.3007}&{3.2259} \end{array}} \right]. $ |
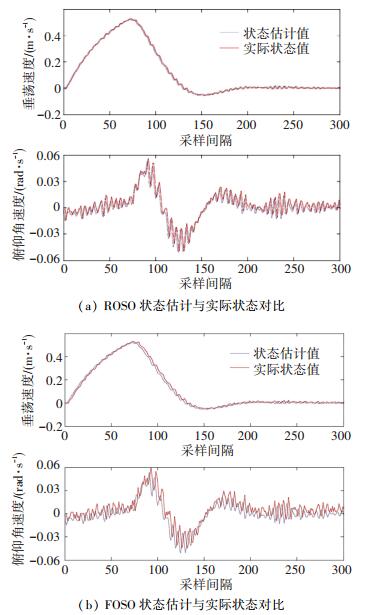
如图 2所示,图 2(a)为通过ROSO得到的状态估计与实际状态的对比,图 2(b)为FOSO得到的状态估计与实际状态的对比.尽管两种状态观测器都可以使状态误差渐进收敛,但是从图中可以看出,ROSO的状态估计性能要优于FOSO.
|
图 2 ROSO与FOSO状态估计性能对比 Figure 2 Comparison of state estimation of ROSO and FOSO |
本文中预测控制器参数选择为:Np=30,Nu=2,Q=INp×Np,R=10.状态变量的初值全部为零. AUV直航速度为uc=1.832 m/s,参考深度轨迹为3.5 m,参考俯仰角为0°,输入输出约束条件为
| $ {\delta _{b\max }} = - {\delta _{b\min }} = {30^ \circ }, $ |
| $ {\delta _{s\max }} = - {\delta _{s\min }} = {25^ \circ }, $ |
| $ \Delta {\delta _{b,s\max }} = - \Delta {\delta _{b,s\min }} = {5^ \circ }/{\rm{s,}} $ |
| $ - {5^ \circ } \le \theta \le {5^ \circ }, $ |
| $ 0\;{\rm{m}} < z < 5\;{\rm{m}}. $ |
其中:δ为前后升降舵舵角,Δδ为舵角变化量.
本文所使用的AUV海浪扰动模型[18]的参数为北太平洋的3级海况,有义波高Hs在0.5~1.25 m之间,并取值Hs=0.88 m,波浪周期为7.5 s,取值概率为16.9%,遭遇角β=45°,拖拽系数Cd=0.65,附加质量系数Cm=1.95,海浪波谱被分为N=271等份.
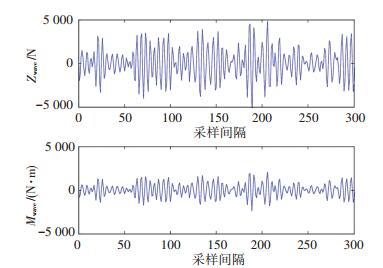
图 3为波浪力和力矩的曲线,在这里可以将海浪扰动视为状态扰动,并将其看作零均值白噪声序列,波浪力和力矩由文献[18]中的方法计算得出,其表达式分别为
|
图 3 波浪力和力矩曲线 Figure 3 Wave force and moment |
| $ \begin{array}{l} {Z_{{\rm{wave}}}} = \int\limits_{{L_0}} {\left[ {{C_d}\frac{{\rho {D_0}}}{2}{{\left( {{\omega _\omega } - \omega } \right)}^2} + } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\left. {{C_m}\frac{{\rho {\rm{ \mathit{ π} }}D_0^2}}{4}\left( {{{\dot \omega }_\omega } - \dot \omega } \right)2} \right]{\rm{d}}x, \end{array} $ | (26) |
| $ \begin{array}{l} {M_{{\rm{wave}}}} = \int\limits_{{L_0}} {\left[ {{C_d}\frac{{\rho {D_0}}}{2}{{\left( {{\omega _\omega } - \omega } \right)}^2} + } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\left. {{C_m}\frac{{\rho {\rm{ \mathit{ π} }}D_0^2}}{4}\left( {{{\dot \omega }_\omega } - \dot \omega } \right)2} \right]x{\rm{d}}x. \end{array} $ | (27) |
式中:L0为AUV长度,ρ为流体密度,D0为AUV的直径,ωω为波谱频率的叠加.可见两者具有相同的形式但是不同的幅值和单位,此外,仿真时主要选取P-M谱主频率附近的多种影响较大的频率进行不规则波的叠加,使仿真结果更真实.
接下来用非线性预测控制(NPC)与本文提出的基于在线线性化的预测控制(PC-NMOL)进行对比,并假设所用的两种方法的全部状态量都可测. 图 4(a)为NPC与PC-NMOL的深度输出曲线对比,图 4(b)为NPC与PC-NMOL的俯仰角输出曲线对比. 图 5(a)、图 5(b)分别为NPC与PC-NMOL的前、后升降舵偏转角度对比.

|
图 4 NPC与PC-NMOL对应的输出曲线对比 Figure 4 Comparison of output of NPC and PC-NMOL |

|
图 5 NPC与PC-NMOL对应的控制量曲线对比 Figure 5 Comparison of control input of NPC and PC-NMOL |
AUV在低航速、近水面航行时,后升降舵对于纵摇控制比较有效,而前升降舵对于深度控制比较有效[19],结合图 4、5也可以看出,在深度达到3.5 m且趋于稳定后,AUV还需要继续保持纵摇姿态稳定,因此后升降舵在零值上下的偏转幅度要明显大于前升降舵,由此验证了前面提到的实际操舵特性.由于本文所用预测控制(PC-NMOL和NPC),属于多变量控制技术,控制对象主要针对多输入多输出(MIMO)系统,因此不用对俯仰角和深度分别设计独立的控制器,仅通过设计一个预测控制器即可完成对MIMO系统的控制.
由于受到波浪的干扰,系统输出和输入曲线存在一定幅度的波动,尽管PC-NMOL的输出跟踪速度与NPC相比稍慢,但是PC-NMOL的深度和俯仰角跟踪效果显然更好一些,同时,与PC-NMOL相比,NPC的升降舵角变化幅度更大,频率更高,即控制量波动更为显著.由此可以看出,针对近水面海浪干扰,本文所提出的PC-NMOL较传统NPC可以更有效的补偿输出和输入上的海浪干扰影响,且鲁棒性更强.
4 结论提出一种基于非线性降维观测器的预测控制来对AUV垂直面运动的深度和俯仰角进行控制.在预测控制器的设计过程中,使用了前级的ROSO对状态量进行了精确的估计,并考虑是实际应用中,升降舵偏转角的物理约束以及AUV姿态的约束,并通过Hildreth二次规划方法进行约束处理.通过仿真验证可以得出,当AUV在垂直面航行时,所提出的控制器能够将AUV控制在理想的深度和俯仰角,同时具有快速的动态响应,并能保证AUV在近水面对于海浪干扰的鲁棒性.
| [1] |
XIANG X, LAPIERRE L, JOUVENCEL B. Smooth transition of AUV motion control: from fully-actuated to under-actuated configuration[J].
Robotics and Autonomous Systems, 2015, 67: 14-22.
DOI: 10.1016/j.robot.2014.09.024 |
| [2] |
YAN Z, YU H, HOU S. Diving control of underactuated unmanned undersea vehicle using integral-fast terminal sliding mode control[J].
Journal of Central South University, 2016, 23: 1085-1094.
DOI: 10.1007/s11771-016-0358-7 |
| [3] |
LAKHEKAR G V, WAGHMARE L M, LONDHE P S. Enhanced dynamic fuzzy sliding mode controller for autonomous underwater vehicles[C]//Underwater Technology (UT). Chennai: IEEE, 2015: 1-7.
http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7108283
|
| [4] |
MAI B L, CHOI H S, YOU S S, et al. Time optimal trajectory design for unmanned underwater vehicle[J].
Ocean Engineering, 2014, 89: 69-81.
DOI: 10.1016/j.oceaneng.2014.06.019 |
| [5] |
ADHAMIMIRHOSSEINI A, YAZDANPANAH M J, AGUIAR A P. Automatic bottom-following for underwater robotic vehicles[J].
Automatica, 2014, 50(8): 2155-2162.
DOI: 10.1016/j.automatica.2014.06.003 |
| [6] |
TSENG Y H, CHEN C C, LIN C H, et al. Tracking controller design for diving behavior of an unmanned underwater vehicle[J].
Mathematical Problems in Engineering, 2013: 2013.
|
| [7] |
HSU S P, LIU T S. Modifications of control loop to improve the depth response of autonomous underwater vehicles[J].
Mathematical Problems in Engineering, 2014, 2014: 1-12.
DOI: 10.1155/2014/324813 |
| [8] |
SUBUDHI B, MUKHERJEE K, GHOSH S. A static output feedback control design for path following of autonomous underwater vehicle in vertical plane[J].
Ocean Engineering, 2013, 63: 72-76.
DOI: 10.1016/j.oceaneng.2013.01.029 |
| [9] |
MAO Z, JIANG B, SHI P. Fault-tolerant control for a class of nonlinear sampled-data systems via a Euler approximate observer[J].
Automatica, 2010, 46(11): 1852-1859.
DOI: 10.1016/j.automatica.2010.06.052 |
| [10] |
FIELD A I. Simulation, modelling, and control of a near-surface underwater vehicle[D]. Vancouver: University of British Columbia, 2000.
https://open.library.ubc.ca/cIRcle/collections/ubctheses/831/items/1.0080953
|
| [11] |
NEŠIC D, TEEL A R, KOKOTOVIC P V. Sufficient conditions for stabilization of sampled-data nonlinear systems via discrete-time approximations[J].
Systems & Control Letters, 1999, 38(4): 259-270.
|
| [12] |
KRATZ W. Characterization of strong observability and construction of an observer[J].
Linear Algebra and its Applications, 1995, 221: 31-40.
DOI: 10.1016/0024-3795(93)00221-K |
| [13] |
SUNDARAPANDIAN V. Reduced order observer design for discrete-time nonlinear systems[J].
Applied Mathematics Letters, 2006, 19(10): 1013-1018.
DOI: 10.1016/j.aml.2005.04.019 |
| [14] |
SUNDARAPANDIAN V. Observer design for discrete-time nonlinear systems[J].
Mathematical and Computer Modelling, 2002, 35(1/2): 37-44.
|
| [15] |
BERTSEKAS D P.
Nonlinear programming[M]. Belmont: Athena Scientific, 1999.
|
| [16] |
CAMACHO E F, ALBA C B.
Model predictive control[M]. Dordrech: Springer Science & Business Media, 2013.
|
| [17] |
WANG L.
Model predictive control system design and implementation using MATLAB®[M]. Dordrech: Springer Science & Business Media, 2009.
|
| [18] |
OSTAFICHUK P M. AUV hydrodynamics and modelling for improved control[D]. Vancouver: University of British Columbia, 2004.
https://open.library.ubc.ca/cIRcle/collections/ubctheses/831/items/1.0080784
|
| [19] |
金鸿章.
船舶控制原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2013.
JIN Hongzhang. Ship control principle[M]. Harbin: Harbin Engineering University Press, 2013. |
 2017, Vol. 49
2017, Vol. 49


