2. 哈尔滨学院 工学院,哈尔滨 150086
2. School of Technology, Harbin University, Harbin 150086, China
捷联惯导系统的罗经对准技术在静基座上的应用已经成熟.为了满足船用捷联惯导系统海上启动的需求,动基座罗经对准已然已成为近年来导航领域的研究热点之一[1].近年来,为了将经典的罗经回路对准方法扩展到动基座对准中,导航领域的研究人员作了大量的工作.文献[1]中,张义利用计程仪作为辅助导航设备,给出罗经对准的速度和位置增量补偿方案,即动基座罗经对准方法.文献[2]中,徐博基于张义的研究成果,将逆向导航解算引入到动基座罗经对准中.文献[3]中,经张俊提出了一种捷联罗经对准时惯性传感器输出校正方法,此方法可以将因为载体运动而产生的陀螺和加速度计输出信号滤除,完成动基座下的罗经自对准.
上述文献都认为计程仪提供的速度信息和捷联惯导系统的惯性测量组合(inertial measurement units, IMU)安装位置处的速度信息一致.实际上计程仪一般安装于船底部,而捷联惯导系统一般安装在船重心处,两者存在一定的安装距离,即存在外杆臂效应[4].外杆臂效应将使得计程仪为捷联惯导系统提供的速度信息存在误差,进而对罗经对准产生影响.本文针对船舶在直航和转弯航行过程中,分析并推导了因外杆臂效应而导致的IMU和计程仪之间速度误差具体形式,然后分析了外杆臂效应的速度误差对罗经对准的影响,最后通过仿真与试验对分析结果进行了验证.
1 外杆臂效应对计程仪测速影响分析由于外杆臂效应的存在,当船体运行时,计程仪测速点处速度与IMU安装处的速度存在误差(捷联惯导应以IMU安装处的速度作为外参考速度进行补偿计算),本章将分别对船体直线航行和转弯航行时的测速误差进行分析.
1.1 船用捷联惯导安装位置船载导航系统中捷联惯导设备一般安装在船体的后半部分,而与惯导系统相配合完成动基座罗经对准的计程仪安装于船体的底部,本文采用电磁计程仪作为辅助测速设备,其通过水流敏感船体的艏艉向速度.设载体坐标系(b系)原点在IMU安装处,水平坐标轴分别指向船体右侧和船体前方,另外一轴由原点指向船体上方. IMU的安装位置和里程计的测速点的相对几何关系在载体坐标系下为
| $ {\mathit{\boldsymbol{D}}^b} = {\left[ {\begin{array}{*{20}{c}} {\Delta {x^b}}&{\Delta {y^b}}&{ - \Delta {z^b}} \end{array}} \right]^{\rm{T}}}. $ | (1) |
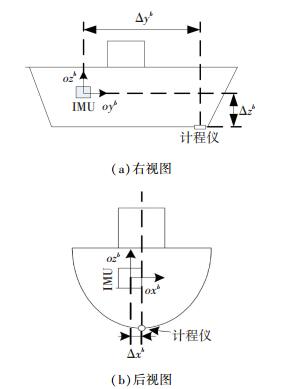
Δxb、Δyb和Δzb分别为3个方向上IMU和计程仪之间的安装距离,如图 1所示.
|
图 1 载体坐标系下IMU与计程仪之间的安装距离 Figure 1 Installation distance between IMU and Log |
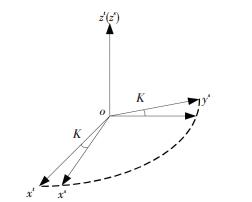
船舶在航行过程中,会存在纵摇和横摇运动,在此引入航向跟踪坐标系(s系),其表示为:y轴随航向转动的当地水平坐标系,z轴与地理坐标系的z轴重合.二者之间关系如图 2所示.
|
图 2 坐标系关系示意图 Figure 2 Schematic diagram of frame of axes |
将IMU和计程仪的安装距离在航向跟踪坐标系中投影,得到
| $ {\mathit{\boldsymbol{D}}^s} = {\left[ {\begin{array}{*{20}{c}} {\Delta {x^s}}&{\Delta {y^s}}&{ - \Delta {z^s}} \end{array}} \right]^{\rm{T}}}. $ | (2) |
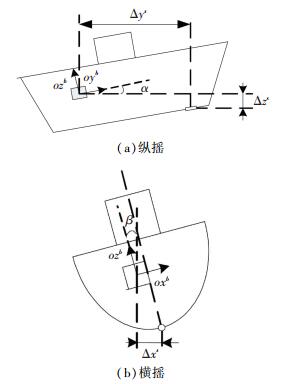
Δxs、Δys和Δzs分别表示航向跟踪坐标系中3个方向上IMU和计程仪之间的安装距离,如图 3所示(其中船体的纵摇角为α,横摇角为β).
|
图 3 航向跟踪坐标系下IMU与计程仪之间的安装距离 Figure 3 Installation distance between IMU and Log under heading following frame of axes |
由图 2、3可以计算航向跟踪坐标系(s系)到载体坐标系(b系)的方向余弦矩阵Csb以及安装距离在b系上的投影为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{D}}^b} = \left[ {\begin{array}{*{20}{c}} {\cos \beta }&0&{ - \sin \beta }\\ 0&1&0\\ {\sin \beta }&0&{\cos \beta } \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos \alpha }&{\sin \alpha }\\ 0&{ - \sin \alpha }&{\cos \alpha } \end{array}} \right] \cdot {\mathit{\boldsymbol{D}}^s} = }\\ {\left[ {\begin{array}{*{20}{c}} {\cos \beta }&{\sin \beta \sin \alpha }&{ - \sin \beta \cos \alpha }\\ 0&{\cos \alpha }&{\sin \alpha }\\ {\sin \beta }&{ - \cos \beta \sin \alpha }&{\cos \beta \cos \alpha } \end{array}} \right] \cdot {\mathit{\boldsymbol{D}}^s}.} \end{array} $ |
这里
| $ \mathit{\boldsymbol{C}}_s^b = \left[ {\begin{array}{*{20}{c}} {\cos \beta }&{\sin \beta \sin \alpha }&{ - \sin \beta \cos \alpha }\\ 0&{\cos \alpha }&{\sin \alpha }\\ {\sin \beta }&{ - \cos \beta \sin \alpha }&{\cos \beta \cos \alpha } \end{array}} \right]. $ |
进一步,有Ds=(Csb)-1Db.
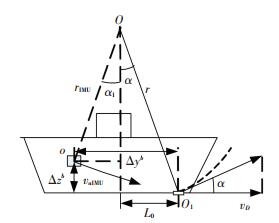
1.2 计程仪测速偏差分析 1.2.1 纵摇情况下的测速偏差分析船舶存在纵摇时,纵摇中心O点在船体重心的延长线上[7],如图 4所示,船体中IMU的纵摇半径rIMU和计程仪的纵摇半径r(船体发生纵摇时,运动状态所处弧形对应的半径)将会变得不一致.
|
图 4 船体纵摇示意图 Figure 4 Schematic diagram of ship pitching |
当船体艏艉速度为vD并存在纵摇运动时,计程仪纵摇半径r与IMU重心位置纵摇半径rIMU会有偏差δr存在
| $ {\delta _r} = r - {r_{{\rm{IMU}}}}. $ | (3) |
其中rIMU为船体行驶中IMU重心所在点的纵摇半径.可以计算出
| $ {r_{{\rm{IMU}}}} = \sqrt {{{\left( { - {L_0} + \Delta {y^b}} \right)}^2} + {{\left( {r\cos \alpha - \Delta {z^b}} \right)}^2}} . $ | (4) |
式中L0为计程仪中心到船体纵摇中心的距离在载体坐标系y轴方向的投影,船体纵摇时,船体速度相对载体坐标系存在夹角α,计程仪测速点速度在载体坐标系上表示为
| $ \mathit{\boldsymbol{v}}_D^b = {\left[ {\begin{array}{*{20}{c}} 0&{{v_D}}&{{{\dot \psi }_\alpha }{L_0}} \end{array}} \right]^{\rm{T}}}. $ | (5) |
设船体纵摇的角速率为
| $ r = \frac{{{v_D}}}{{{{\dot \psi }_\alpha }\cos \alpha }}. $ | (6) |
根据图 4和式(4)、(5),得到IMU的重心位置的速率为
| $ {v_{\alpha {\rm{IMU}}}} = {{\dot \psi }_\alpha }{r_{{\rm{IMU}}}} = {{\dot \psi }_\alpha }\sqrt {{{\left( { - {L_0} + \Delta {y^b}} \right)}^2} + {{\left( {\frac{{{v_D}}}{{{{\dot \psi }_\alpha }}} - \Delta {z^b}} \right)}^2}} . $ | (7) |
将IMU重心位置速度在载体坐标系上表示为
| $ \begin{array}{l} \mathit{\boldsymbol{v}}_{\alpha {\rm{IMU}}}^b = {\left[ {\begin{array}{*{20}{c}} 0&{{v_{\alpha {\rm{IMU}}}}\cos {\alpha _1}}&{ - {v_{\alpha {\rm{IMU}}}}\sin {\alpha _1}} \end{array}} \right]^{\rm{T}}} = \\ \;\;\;\;\;\;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}} 0&{{v_{\rm{D}}} - {{\dot \psi }_\alpha }\Delta {z^b}}&{{{\dot \psi }_\alpha }\left( {{L_0} - \Delta {y^b}} \right)} \end{array}} \right]^{\rm{T}}}. \end{array} $ | (8) |
其中
所以船体纵摇时,外杆臂效应引起的计程仪测速误差为
| $ \mathit{\boldsymbol{\delta }}{\mathit{\boldsymbol{v}}_\alpha } = \mathit{\boldsymbol{v}}_D^b - \mathit{\boldsymbol{v}}_{\alpha {\rm{IMU}}}^b = {\left[ {\begin{array}{*{20}{c}} 0&{{{\dot \psi }_\alpha }\Delta {z^b}}&{{{\dot \psi }_\alpha }\Delta {y^b}} \end{array}} \right]^{\rm{T}}}. $ | (9) |
船体产生横摇时,船体的航向速度没有发生改变,计程仪测量的船体艏艉速度不会产生变化,航向方向上的IMU速度也不会因为外杆臂效应而产生误差.但在船体横摇过程中,IMU会在载体坐标系的xoz平面内有速度分量,这部分速度是计程仪不能提供的,这就引起了测速误差.船舶产生横摇时,横摇中心O点是船体重心[7],如图 5所示.

|
图 5 船体横摇示意图 Figure 5 Schematic diagram of ship rolling |
设船体横摇时艏艉向速度为vD,计程仪速度输出在载体坐标系上表示为
| $ \mathit{\boldsymbol{v}}_D^b = {\left[ {\begin{array}{*{20}{c}} 0&{{v_D}}&0 \end{array}} \right]^{\rm{T}}}. $ | (10) |
横摇时,船体横摇的角速率为
| $ {v_\beta } = {{\dot \psi }_\beta }\sqrt {\left( {L_1^2 + {{\left( {\Delta {x^b}} \right)}^2}} \right.} . $ | (11) |
式中L1为船体重心到IMU中心的距离在载体坐标系x轴方向的投影,根据图 5可得IMU在载体坐标系上的速度为
| $ \mathit{\boldsymbol{v}}_{\beta {\rm{IMU}}}^b = {\left[ {\begin{array}{*{20}{c}} {{{\dot \psi }_\beta }{L_1}}&{{v_D}}&{{{\dot \psi }_\beta }\Delta {x^b}} \end{array}} \right]^{\rm{T}}}. $ | (12) |
所以船体横摇时,由外杆臂效应引起的计程计测速误差为
| $ {\mathit{\boldsymbol{\delta v}}_\beta } = \mathit{\boldsymbol{v}}_D^b - \mathit{\boldsymbol{v}}_{\beta {\rm{IMU}}}^b = {\left[ {\begin{array}{*{20}{c}} { - {{\dot \psi }_\beta }{L_1}}&0&{ - {{\dot \psi }_\beta }\Delta {x^b}} \end{array}} \right]^{\rm{T}}}. $ | (13) |
船舶在转弯运行时,自身也为了提供转弯所需要的向心力而发生一定的角度倾斜,产生较大幅度的横摇角.假设船舶在转弯运动时,船体的速度和转弯角将会在当地水平面内,因此本文将船体的安装误差和运动参数投影到航向跟踪坐标系中进行解算.
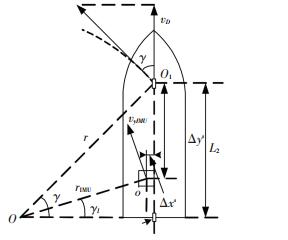
船舶转弯航行时,船体绕舵机转动,舵机一般安装于船体的尾部[5],如图 6所示.船体中IMU的转弯半径和计程仪的转弯半径将会变得不一致.
|
图 6 船体转弯示意图 Figure 6 Schematic diagram of ship turning |
设船体转弯时艏艉向速度为vD,与船体纵摇情况下直线航行时相似,计程仪安装处转弯半径r与实际IMU中心处转弯半径会有误差δr存在
| $ {\delta _r} = r - {r_{{\rm{IMU}}}} $ |
其中rIMU为实际行驶中IMU重心所在点的转弯半径.根据图 6,可以计算得出
| $ {r_{{\rm{IMU}}}} = \sqrt {{{\left( {{L_2} - \Delta {y^s}} \right)}^2} + {{\left( {r\cos \gamma - \Delta {x^s}} \right)}^2}} . $ | (14) |
式中L2为计程仪中心到舵机中心的距离在载体坐标系x轴方向的投影,船体转弯时,船体速度相对当地水平坐标系(S系)存在夹角γ,则计程仪测速点处速度在载体坐标系上可表示为
| $ \mathit{\boldsymbol{v}}_D^b = C_s^b{\left[ {\begin{array}{*{20}{c}} { - {{\dot \psi }_\gamma }{L_2}}&{{v_D}}&0 \end{array}} \right]^{\rm{T}}}. $ |
设船舶转弯时,船体在航向跟踪坐标系Z轴的角速率为
| $ r = \frac{{{r_D}}}{{{{\dot \psi }_\gamma }\cos \gamma }}. $ | (15) |
根据式(14)、(15),可得IMU重心位置的转弯速率为
| $ {v_{\gamma {\rm{IMU}}}} = {{\dot \psi }_\gamma }{v_{\psi {\rm{IMU}}}} = {{\dot \psi }_\gamma }\sqrt {{{\left( {{L_2} - \Delta {y^s}} \right)}^2} + {{\left( {\frac{{{r_D}}}{{{{\dot \psi }_\gamma }}} - \Delta {x^s}} \right)}^2}} . $ | (16) |
将IMU重心位置转弯速度在载体坐标系上分解为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{v}}_{\gamma {\rm{IMU}}}^b = C_s^b{{\left[ {\begin{array}{*{20}{c}} { - {v_{\gamma {\rm{IMU}}}}\sin {\gamma _1}}&{{v_{\gamma {\rm{IMU}}}}\cos {\gamma _1}}&0 \end{array}} \right]}^{\rm{T}}} = }\\ {C_s^b{{\left[ {\begin{array}{*{20}{c}} {{{\dot \psi }_\gamma }\left( {\Delta {y^s} - {L_2}} \right)}&{{v_D} - {{\dot \psi }_\gamma }\Delta {x^s}}&0 \end{array}} \right]}^{\rm{T}}}.} \end{array} $ | (17) |
其中
所以由外杆臂效应引起的转弯时计程仪测速误差在载体坐标系下表示为
| $ \delta {\mathit{\boldsymbol{v}}_\gamma } = \mathit{\boldsymbol{v}}_D^b - \mathit{\boldsymbol{v}}_{\gamma {\rm{IMU}}}^b = T \cdot {\left[ {\begin{array}{*{20}{c}} { - {{\dot \psi }_\gamma }\Delta {y^s}}&{{{\dot \psi }_\gamma }\Delta {x^s}}&0 \end{array}} \right]^{\rm{T}}}. $ | (18) |
式中T为航向跟踪坐标系到载体坐标系的方余弦矩阵.
2 外杆臂效应对罗经对准的影响分析 2.1 罗经对准过程动基座罗经回路对准流程如图 7所示.其中,Vdvlb为b系下多普勒程仪提供的外速度.
在载体航行过程中的动基座罗经对准需要补偿的部分为ωiep、ωepp、Bp.三者的计算方法[1]为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\omega }}_{ie}^p = {{\left[ {\begin{array}{*{20}{c}} 0&{\mathit{\Omega }\cos \varphi }&{\mathit{\Omega }\sin \varphi } \end{array}} \right]}^{\rm{T}}},}\\ {\mathit{\boldsymbol{\omega }}_{ep}^p = {{\left[ {\begin{array}{*{20}{c}} { - \frac{{{v_N}}}{R}}&{\frac{{{v_E}}}{R}}&{\frac{{{v_E}}}{{R {\rm c}\tan \varphi }}} \end{array}} \right]}^{\rm{T}}},}\\ {{\mathit{\boldsymbol{B}}^p}\left( {\mathit{\boldsymbol{\omega }}_{ep}^p + 2\mathit{\boldsymbol{\omega }}_{ie}^p} \right) \times {\mathit{\boldsymbol{v}}^p}.} \end{array} $ | (19) |
其中Ω为地球的自转角速度,R为地球半径,φ为载体所在纬度.
如果要补偿计算上式中的3项,需要计程仪提供速度信息.因为利用到计程仪的速度信息,所以外杆臂效应导致的计程仪测量偏差将影响动基座罗经对准.
2.2 等效对准误差角在外杆臂效应引起的速度偏差δvn的作用下,运动角速度ωepp的误差可以表示为
| $ \delta \mathit{\boldsymbol{\omega }}_{ep}^p = {\left[ {\begin{array}{*{20}{c}} { - \frac{{\delta {v_N}}}{R}}&{\frac{{\delta {v_E}}}{R}}&{\frac{{\delta {v_E}}}{{R{\rm c}\tan \varphi }}} \end{array}} \right]^{\rm{T}}}. $ | (20) |
在捷联惯性导航系统的姿态解算中,捷联矩阵的修正过程[6]为
| $ \begin{array}{*{20}{c}} {\omega _{pb}^b = \omega _{ib}^b - C_p^b\left( {\omega _{ie}^p + \omega _{ep}^p} \right),}\\ {\dot C_b^p = C_b^p\mathit{\Omega }_{pb}^b.} \end{array} $ | (21) |
经由罗经回路对准计算出修正角速度ωcp,然后对角速度进行修正,可以得到
| $ \omega _{pb}^b = \omega _{ib}^b - C_p^b\left( {\omega _{ie}^p + \omega _{ep}^p} \right) - C_p^b\left( {\omega _c^p} \right). $ | (22) |
由于存在运动角速度误差δωepp,式(19)变为
| $ \begin{array}{l} \omega _{pb}^{'b} = \omega _{ib}^b - C_p^b\left( {\omega _{ie}^p + \omega _{ep}^p} \right) - C_p^b\left( {\omega _c^p} \right) = \\ \;\;\;\;\;\;\;\;\;\omega _{ib}^b - C_p^b\left( {\delta \omega _{ep}^p} \right) - C_p^b\left( {\omega _{ie}^p + \omega _{ep}^p} \right) - C_p^b\left( {\omega _c^p} \right). \end{array} $ | (23) |
当存在陀螺漂移εb时,式(19)可改成
| $ \begin{array}{l} \omega _{pb}^{'b} = \omega _{ib}^b + {\varepsilon _b} - C_p^b\left( {\omega _{ie}^p + \omega _{ep}^p} \right) - C_p^b\left( {\omega _c^p} \right) = \omega _{ib}^b - \\ \;\;\;\;\;\;\;\;\;C_p^b\left( {{\varepsilon _p}} \right) - C_p^b\left( {\omega _{ie}^p + \omega _{ep}^p} \right) - C_p^b\left( {\omega _c^p} \right). \end{array} $ | (24) |
比较式(23)、(24)可见,运动角速度误差δωepp与陀螺漂移εp作用形式相同,可将δωepp看作陀螺漂移.因此可用分析器件常值误差的方法来分析外杆臂效应对罗经对准过程的影响.常值器件误差作用下的罗经法对准误差为
| $ \left\{ \begin{array}{l} {\varphi _x} = - \frac{1}{g} \cdot \Delta {A_N} - \frac{{{k_1}{k_2}}}{{g{k_U}}} \cdot {\varepsilon _U},\\ {\varphi _y} = \frac{1}{g} \cdot \Delta {A_E},\\ {\varphi _z} = \frac{1}{{\mathit{\Omega }\cos \varphi }} \cdot {\varepsilon _E} + \frac{{{k_2}{k_N}}}{{{k_U}\mathit{\Omega }\cos \varphi }} \cdot {\varepsilon _U}. \end{array} \right. $ | (25) |
根据上式罗经对准过程中,由δωepp引起的误差为
| $ \left\{ \begin{array}{l} \varphi _x^{{\delta _{{{\rm{v}}_1}}}} = - \frac{{{k_1}{k_2}}}{{g{k_U}}} \cdot \frac{{\delta {v_E}}}{{R{\rm{c}}\tan \varphi }},\\ \varphi _z^{{\delta _{{{\rm{v}}_1}}}} = \frac{1}{{\mathit{\Omega }\cos \varphi }} \cdot \left( { - \frac{{\delta {v_N}}}{R}} \right) + \frac{{{k_N}{k_2}}}{{{k_3}}} \cdot \frac{{\delta {v_E}}}{{R{\rm{c}}\tan \varphi }}. \end{array} \right. $ | (26) |
其中k3=kUΩcos φ,k1、k2、kN、kU为文献[1]中定义的罗经对准参数.
捷联惯导系统中有害加速度Bp计算公式为
| $ {B^p} = \left( {\omega _{ep}^p + 2\omega _{ie}^p} \right) \times {v^p}. $ | (27) |
不考虑天向通道,外杆臂效应影响下的有害加速度Bp引起的加速度误差为
| $ \left\{ \begin{array}{l} B_E^p = \left( {2\mathit{\Omega }\sin \varphi + \frac{{{v_E}}}{{R{\rm{c}}\tan \varphi }}} \right) \cdot {v_N},\\ B_N^p = - \left( {2\mathit{\Omega }\sin \varphi + \frac{{{v_E}}}{{R{\rm{c}}\tan \varphi }}} \right) \cdot {v_E}. \end{array} \right. $ | (28) |
若考虑外杆臂效应的东向和北向误差,则式(28)可以写为
| $ \left\{ \begin{array}{l} B_E^{'p} = \left( {2\mathit{\Omega }\sin \varphi + \frac{{{v_E} + \delta {v_E}}}{{R{\rm{c}}\tan \varphi }}} \right) \cdot \left( {{v_N} + \delta {v_N}} \right),\\ B_N^{'p} = - \left( {2\mathit{\Omega }\sin \varphi + \frac{{{v_E} + \delta {v_E}}}{{R{\rm{c}}\tan \varphi }}} \right) \cdot \left( {{v_E} + \delta {v_E}} \right). \end{array} \right. $ | (29) |
将式(29)、(28)相减,可近似得到有害加速度误差为
| $ \left\{ \begin{array}{l} \delta B_E^p = 2\mathit{\Omega }\sin \varphi \cdot \delta {v_N} + \frac{{\delta {v_N} \cdot {v_E} + \delta {v_E} \cdot {v_N} + \delta {v_E} \cdot \delta {v_N}}}{{R{\rm c}\tan \varphi }},\\ \delta B_N^p = - \left( {2\mathit{\Omega }\sin \varphi \cdot \delta {v_E} + \frac{{2\delta {v_E} \cdot {v_E} + \delta v_E^2}}{{R{\rm{c}}\tan \varphi }}} \right). \end{array} \right. $ | (30) |
从式(30)中可以知道,纬度的改变会影响加速度误差的大小,但是在一般的行驶过程中,纬度φ的变化很小,一般不予考虑.在罗经回路中,系统对高频信号有着很强的抑制作用,所以本文只考虑常值部分.
根据式(30)可以得到常值加速度误差作用下的误差角为
| $ \left\{ \begin{array}{l} \varphi _x^{\delta {v_2}} = \frac{1}{g} \cdot \left( {2\mathit{\Omega }\sin \varphi \cdot \delta {v_N}} \right),\\ \varphi _y^{\delta {v_2}} = - \frac{1}{g} \cdot \left( {2\mathit{\Omega }\sin \varphi \cdot \delta {v_E}} \right). \end{array} \right. $ | (31) |
由此可见,由于外杆臂效应影响下的有害加速度Bp对对准的影响主要是水平误差.综合ωepp和Bp两部分的影响,可以得出外杆臂引起的速度误差对罗经对准的最终影响为
| $ \left\{ \begin{array}{l} \varphi _x^{\delta v} = \varphi _x^{\delta {v_1}} + \varphi _x^{\delta {v_2}} = \frac{1}{g} \cdot \left( {2\mathit{\Omega }\sin \varphi \cdot \delta {v_N}} \right) - \frac{{{k_1}{k_2}}}{{g{k_U}}} \cdot \frac{{\delta {v_E}}}{{R{\rm{c}}\tan \varphi }},\\ \varphi _y^{\delta v} = \varphi _y^{\delta {v_1}} + \varphi _y^{\delta {v_2}} = - \frac{1}{g} \cdot \left( {2\mathit{\Omega }\sin \varphi \cdot \delta {v_E}} \right),\\ \varphi _z^{\delta v} = \varphi _z^{\delta {v_1}} + \varphi _z^{\delta {v_2}} = \frac{1}{{\mathit{\Omega }\cos \varphi }} \cdot \left( { - \frac{{\delta {v_N}}}{R}} \right) + \frac{{{k_N}{k_2}}}{{{k_3}}} \cdot \frac{{\delta {v_E}}}{{R{\rm{c}}\tan \varphi }}. \end{array} \right. $ | (32) |
结合船体航行时的测速误差表达式,得到不同航行状态下的罗经对准修正影响方程.
1) 船舶存在纵摇的直航运动状态为
| $ {\mathit{\boldsymbol{\varphi }}^{\delta v}} = \left[ {\begin{array}{*{20}{c}} { - \frac{{{k_1}{k_2}}}{{g{k_U}R{\rm{c}}\tan \varphi }}}&{\frac{{2\mathit{\Omega }\sin \varphi }}{g}}&0\\ { - \frac{{2\mathit{\Omega }\sin \varphi }}{g}}&0&0\\ {\frac{{{k_N}{k_2}}}{{{k_3}R{\rm{c}}\tan \varphi }}}&{ - \frac{1}{{\mathit{\Omega }\cos \varphi }}}&0 \end{array}} \right] \cdot C_b^n\left[ {\begin{array}{*{20}{c}} 0\\ {{{\dot \psi }_\alpha }\Delta {z^b}}\\ {{{\dot \psi }_\alpha }\Delta {y^b}} \end{array}} \right]. $ | (33) |
2) 船舶存在横摇时的直航运动状态为
| $ {\mathit{\boldsymbol{\varphi }}^{\delta v}} = \left[ {\begin{array}{*{20}{c}} { - \frac{{{k_1}{k_2}}}{{g{k_U}R{\rm{c}}\tan \varphi }}}&{\frac{{2\mathit{\Omega }\sin \varphi }}{g}}&0\\ { - \frac{{2\mathit{\Omega }\sin \varphi }}{g}}&0&0\\ {\frac{{{k_N}{k_2}}}{{{k_3}R{\rm{c}}\tan \varphi }}}&{ - \frac{1}{{\mathit{\Omega }\cos \varphi }}}&0 \end{array}} \right] \cdot \boldsymbol{C}_b^n\left[ {\begin{array}{*{20}{c}} { - {{\dot \psi }_\beta }{L_1}}\\ 0\\ {{{\dot \psi }_\beta }\Delta {x^b}} \end{array}} \right]. $ | (34) |
3) 船舶转弯航行运动状态为
| $ {\mathit{\varphi }^{\delta v}} = \left[ {\begin{array}{*{20}{c}} { - \frac{{{k_1}{k_2}}}{{g{k_U}R{\rm{c}}\tan \varphi }}}&{\frac{{2\mathit{\Omega }\sin \varphi }}{g}}&0\\ { - \frac{{2\mathit{\Omega }\sin \varphi }}{g}}&0&0\\ {\frac{{{k_N}{k_2}}}{{{k_3}R{\rm{c}}\tan \varphi }}}&{ - \frac{1}{{\mathit{\Omega }\cos \varphi }}}&0 \end{array}} \right] \cdot C_b^nT\left[ {\begin{array}{*{20}{c}} { - {{\dot \psi }_\gamma }\Delta {y^s}}\\ {{{\dot \psi }_\gamma }\Delta {x^s}}\\ 0 \end{array}} \right]. $ | (35) |
4) 船舶实际相互耦合时的运动状态为
| $ {\mathit{\varphi }^{\delta v}} = \left[ {\begin{array}{*{20}{c}} { - \frac{{{k_1}{k_2}}}{{g{k_U}R{\rm{c}}\tan \varphi }}}&{\frac{{2\mathit{\Omega }\sin \varphi }}{g}}&0\\ { - \frac{{2\mathit{\Omega }\sin \varphi }}{g}}&0&0\\ {\frac{{{k_N}{k_2}}}{{{k_3}R{\rm{c}}\tan \varphi }}}&{ - \frac{1}{{\mathit{\Omega }\cos \varphi }}}&0 \end{array}} \right] \cdot C_b^n\delta {v^b}. $ | (36) |
其中δvb=δvα+δvβ+δvγ.通常情况下,外杆臂引起的速度偏差对水平和方位误差角产生影响.水平误差角所受影响等效为加速度计零偏影响;方位误差角所受影响等效于东向陀螺漂移影响,方位误差角所受影响较大.表明外杆臂效应对罗经对准的影响主要体现在方位角上.
3 仿真分析为了观察前面内容所描述的外杆臂效应引起的计程仪测速偏差对罗经对准过程的影响,并验证误差分析的正确性,下面通过仿真来分析船舶在不同情况下的罗经对准过程.
仿真中采用了文献[1]提出的动基座罗经对准方法,罗经对准参数选取如下:k1=k2=0.0113,kE=kN=9.81×10-6,kU=4.1×10-6.捷联惯导首先经历5 min静基座粗对准过程,之后进入罗经对准阶段.在罗经对准阶段中,设定船舶航行与运动状况分别为下述3种情况:1)匀速直航(速率8 m/s)加纵摇(正弦形式、幅度6°、周期为8 s);2)匀速直航(速率8 m/s)加横摇(正弦形式、幅度6°、周期为8 s);3)改变航向(速率8 m/s、正弦形式、幅度6°、周期为8 s).为了在相同的船舶运动条件下比较,3种情况设定的正弦运动相同. IMU安装重心与计程仪测速点之间的安装距离参数分别为L1=1 m,Δxs=0.2 m,Δzb=3 m,Δys=25 m.
其他仿真条件设置:纬度45.779 6°,经度126.677 8°;选择中等精度IMU,陀螺漂移选取0.01°/h,加速度计常值偏差选取0.000 1g.
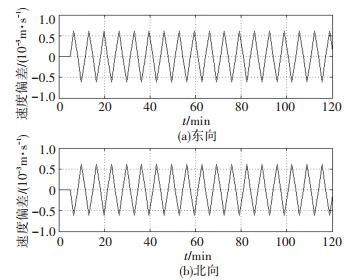
情况1下的外杆臂效应引起的测速偏差以及引起的罗经对准误差分别如图 8、9所示.
|
图 8 情况1下的测速偏差 Figure 8 Velocity differences under scenario 1 |
|
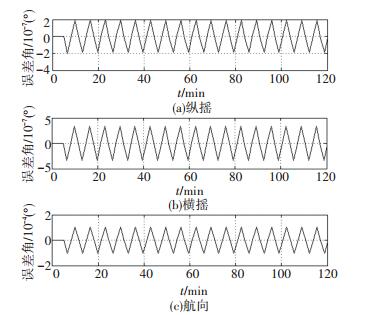
图 9 情况1下的姿态误差 Figure 9 Attitude errors under scenario 1 |
如图 8、9所示,船舶在情况1所描述的纵摇下,IMU安装中心与计程仪测速点之间的安装距离带来的外杆臂效应会引入10-4量级的东向和北向速度偏差,进一步,该偏差会导致10-7量级的纵摇、横摇误差和10-4量级的航向误差.
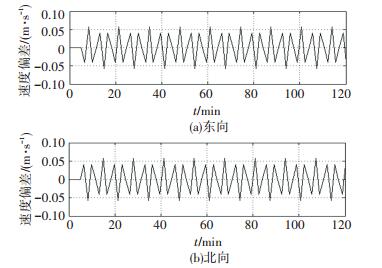
情况2下的外杆臂效应引起的测速偏差以及引起的罗经对准误差分别如图 10、11所示.
|
图 10 情况2下的测速偏差 Figure 10 Velocity differences under scenario |
|
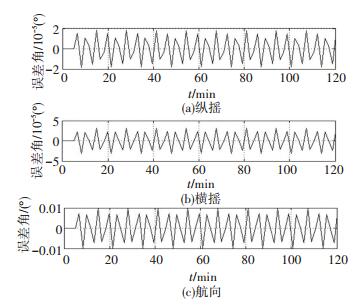
图 11 情况2下的姿态误差 Figure 11 Attitude errors under scenario 2 |
如图 10、11所示,船舶在情况2所描述的横摇下,外杆臂效应会引入10-2量级的东向和北向速度偏差,进一步,该偏差会导致10-5量级的纵摇、横摇误差和10-2量级的航向误差.
情况3下的外杆臂效应引起的测速偏差以及引起的罗经对准误差分别如图 12、13所示.

|
图 12 情况3下的测速偏差 Figure 12 Velocity differences under scenario 3 |
|
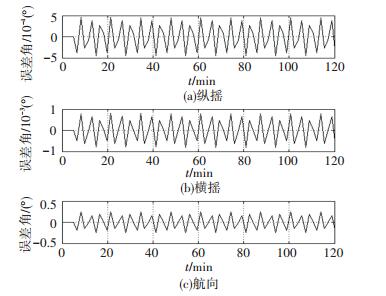
图 13 情况3下的姿态误差 Figure 13 Attitude errors under scenario 3 |
如图 12、13,船舶在情况3所描述的航向变化下,外杆臂效应会引入1 m/s左右的东向和北向速度偏差,进一步,该偏差会导致10-3量级的纵摇、横摇误差和10-1量级的航向误差.
由上可知,在具有相同的摇摆周期、幅度时,航向变化导致的外杆臂效应会引入的东向和北向速度偏差最大,其次为横摇,最后为纵摇;相应地,姿态误差排序为航向变化大于横摇,横摇大于纵摇.再有,各种情况下,罗经对准的航向误差大于水平误差,即外杆臂效应对于罗经对准的影响主要体现在航向对准结果上.
为了观察不同组IMU安装中心与计程仪测速点之间的安装距离参数对于罗经对准过程和结果的影响,经分析计程仪测速误差以及姿态误差表达式可知:IMU安装中心与计程仪测速点之间的安装距离同测速误差和姿态误差成正比关系,下面进行验证,这里仅验证两者距离增大的情况,本文对情况3中的安装距离参数作修改,得到情况4.
情况4改变航向(速率8 m/s、正弦形式、幅度6°、周期为8 s). IMU安装重心与计程仪测速点之间的安装距离参数分别为L1=2 m,Δxs=0.4 m,Δzb=5 m,Δys=45 m.
情况4下的外杆臂效应引起的测速偏差以及引起的罗经对准误差分别如图 14、15所示.

|
图 14 情况4下的测速偏差 Figure 14 Velocity differences under scenario 4 |
|
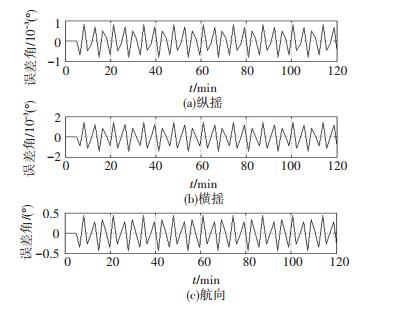
图 15 情况4下的姿态误差 Figure 15 Attitude errors under scenario 4 |
如图 14、15,船舶在情况4所描述的航向变化下,外杆臂效应会引入2 m/s左右的东向和北向速度偏差,进一步,该偏差会导致0.001°的纵摇、横摇误差(约为情况3的两倍)和0.5°的航向误差(约为情况3的两倍).由此可见,加大IMU安装中心与计程仪测速点之间的安装距离,外杆臂效应会引入东向和北向速度偏差,纵摇、横摇、航向误差均会增大.
从以上仿真结果可以看出,计程仪的测速偏差与罗经对准的失准角周期类似,用MATLAB对两组信号使用快速傅里叶变换进行频谱分析[9]可知,二者的频率范围比较接近,均在25 Hz以下,因此不适合使用数字滤波器来对计程仪的测速偏差进行滤波[10],从而无法实现该误差的在线补偿.
4 结论1) IMU安装中心与计程仪测速点之间的安装距离会导致捷联惯导系统罗经对准中出现外杆臂效应.
2) 外杆臂效应会导致测速偏差和罗经对准姿态误差,姿态误差在航向改变时最大并且主要体现在航向对准结果上.
3) 加大或减小IMU安装中心与计程仪测速点之间的安装距离,外杆臂效应引入的测速偏差和姿态误差均会增大或减小.
| [1] |
张义. 舰船捷联惯性系统初始对准技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
ZHANG Yi. Research on initial alignment ofstrapdown inertial navigation system[D].Harbin:Harbin Engineering University, 2012. http: //cdmd. cnki. com. cn/Article/CDMD-10217-1012518756. htm |
| [2] |
XU Bo, LIU Yang. Error analysis and compensation of gyrocompass alignment for SINS on moving base[J].
Mathematical Problems in Engineering, 2014, 2014: 1-18.
DOI: 10.1155/2014/373575 |
| [3] |
经张俊, 程向红, 王宇. 捷联罗经的动基座自对准技术[J].
中国惯性技术学报, 2009, 17(4): 408-412.
JING Zhangjun, CHENG Xianghong, WANG Yu. Self alignment technique of moving base of Strapdown gyrocompass[J]. Journal of Chinese Inertial Technology, 2009, 17(4): 408-412. |
| [4] |
严恭敏. 车载自主定位定向系统研究[D]. 西安: 西北工业大学, 2006.
YAN Gongmin. Research on vehicle autonomous positioning and orientation system[D]. Xi′an:Northwestern Polytechnical University, 2006. http: //cdmd. cnki. com. cn/Article/CDMD-10699-2007035473. htm |
| [5] |
孙伟, 孙枫, 刘繁明. 光纤陀螺旋转捷联惯导系统的发展与应用[J].
传感器与微系统, 2012, 31(11): 1-4.
SUN Wei, SUN Feng, LIU Fanming. Development and application of fiber optic gyro rotation strapdown inertial navigation System[J]. Sensors and micro systems, 2012, 31(11): 1-4. DOI: 10.3969/j.issn.1000-9787.2012.11.001 |
| [6] |
陈哲. 捷联惯性导航系统原理[M]. 北京: 宇航出版社, 1986:
CHEN Zhe. Principle of strapdown inertial navigation system[M].Beijing: Aerospace publishing house, 1986: 137-142. |
| [7] |
梁霄, 李巍.
船舶操纵性与耐波性[M]. 大连: 大连海事大学, 2012: 12-20.
LIANG Xiao, LI Wei. Ship maneuverability and seakeeping[M]. Dalian: Dalian Maritime University, 2012: 12-20. |
| [8] |
HONG S, LEE M H, KWON S H, et al. A car test for the estimation of GPS/INS alignment errors[J].
IEEE Transactions on Intelligent Transportation Systems, 2004, 5(3): 208-218.
DOI: 10.1109/TITS.2004.833771 |
| [9] |
孙伟, 孙枫. 基于SINS的杆臂效应误差补偿方法研究[J].
控制与决策, 2012, 27(6): 1386-1390.
SUN Wei, SUN Feng. Study on the lever arm effect error compensation method based on SINS[J]. Control and decision making, 2012, 27(6): 1386-1390. |
| [10] |
翁浚, 游金川, 秦永元, 等. 载车SINS/OD杆臂在线补偿算法[J].
传感技术学报, 2013, 26(9): 1232-1235.
WENG Jun, YOU Jinchuan, QIN Yongyuan, et al. The vehicle SINS/OD arm online compensation algorithm[J]. Journal of sensing Technology, 2013, 26(9): 1232-1235. |
 2017, Vol. 49
2017, Vol. 49



