近年来,随着前列腺肿瘤发病率持续增长,机器人辅助微创前列腺根切术成为前列腺癌治疗的重要方法[1].然而,由于医生仅能从内窥镜视野中观察手术情况,无法获知组织的深度信息,容易造成神经血管束或尿道等组织的创伤,产生术后阳痿、尿失禁等严重并发症[2].超声图像能透视成像,并且具有成像要求低,对病患无伤害的优点.将超声成像技术和机器人技术结合,可以在手术中实现对器械周围组织的超声实时追踪成像,为医生提供多维视角,提高手术成功率[3].
为了实现超声探头成像平面对手术器械的实时追踪,需要完成超声辅助系统和手术机器人系统的配准.针对手术室空间有限以及在保证配准精度的前提下降低成本,采用在超声图像中识别固连在手术机器人末端的器械轮廓的方法,实现两套系统的配准[4].本文中使用组织钳作为配准工具,即需要在超声图像中,通过对图像的分割算法,识别组织钳的轮廓,完成系统之间关系的建立.分割算法的精度,将直接影响到配准的精度.
常规的图像分割算法一般包括基于阈值的分割、OTSU算法、水平集分割算法和参数活动轮廓分割(Snake)等,这些算法在其适用的场合中均具有相应的优势[5-10].在本研究中,由于手术器械的形状尺寸是已知的,因此采用结合模型进行分割的参数活动轮廓分割法比较合适.传统的Snake分割法采用各个能量项的加和形式构成总的泛能量,通过迭代求解的方式获得收敛的轮廓,并在分割过程中保证曲线的连续性,具有很方便的扩展性质[11].但同时,这种算法通过贪心策略搜索能量最小化的曲线轮廓,容易在迭代过程中陷入局部极小值[12].
微创器械的轮廓形状和尺寸已知,在传统的Snake分割算法中融入器械轮廓信息作为先验知识,能提高分割过程的准确性和收敛速度.使用归一化傅里叶描述子从频域角度对器械轮廓进行描述,能避免先验论廓和分割轮廓采样点个数不一致导致的信息丢失.通过构建傅里叶描述子能量函数,并将其融入传统Snake模型中,能实现对轮廓整体形状的约束.通过迭代方式求出能量极值时的分割轮廓,能避免陷入局部极值,提高分割精度.
1 归一化傅里叶描述子为了将目标区域轮廓曲线作为先验知识应用到模型中,需要使用合理的方法表述轮廓.傅里叶描述子是目标区域轮廓曲线的傅里叶变换系数.根据傅里叶变换的性质,傅里叶描述子与轮廓的形状、位置、尺度、旋转角度和序列起点等均有关.在保证形状尺寸条件下,需要对剩余的因素进行归一化处理.
假设轮廓序列点共有N个,表示为{x(n)+jy(n)|n=0, 1, …, N-1},它们的傅里叶描述子序列为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{z}}\left( k \right) = \mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{x}} + {\rm{j}}\mathit{\boldsymbol{y}}} \right) = \sum\limits_{n = 0}^{N - 1} {\left( {\mathit{\boldsymbol{x}}\left( n \right) + {\rm{j}}\mathit{\boldsymbol{y}}\left( n \right)} \right)} \cdot {{\rm{e}}^{ - {\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}kn}}{N}}},}\\ {k = 0,2, \cdots ,N - 1.} \end{array} $ |
假设将轮廓曲线序列起始点平移a像素长度,放大r倍,旋转h角度,以及平移(x0, y0)像素,得到新的傅里叶描述子z′(k)[13]
| $ \begin{array}{l} \mathit{\boldsymbol{z'}}\left( k \right) = \mathit{\boldsymbol{F}}\left[ {\left( {\mathit{\boldsymbol{x'}} + {\rm{j}}\mathit{\boldsymbol{y'}}} \right)r{{\rm{e}}^{{\rm{j}}h}} + \left( {{x_0} + {\rm{j}}{y_0}} \right)} \right] = \\ \;\;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} r{{\rm{e}}^{{\rm{j}}h}}z\left( 0 \right) + \mathit{\boldsymbol{F}}\left( {{x_0} + {\rm{j}}{y_0}} \right),\;\;\;\;k = 0;\\ r{{\rm{e}}^{{\rm{j}}h}}{{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}}}{N}ka}}\mathit{\boldsymbol{z}}\left( k \right),\;\;\;\;k = 1,2, \cdots ,N - 1. \end{array} \right. \end{array} $ |
当k=1, 2, …, N-1时,有
| $ \left\| {\mathit{\boldsymbol{z'}}\left( k \right)} \right\| = r\left\| {{{\rm{e}}^{{\rm{j}}h}}{{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}ka}}{N}}}\mathit{\boldsymbol{z}}\left( k \right)} \right\| = \left\| {z\left( k \right)} \right\|. $ |
式中‖·‖表示对元素进行取模操作,x′(n)+jy′(n)= x(n+a)+jy(n+a).
2 先验Snake模型Kass等[11]提出了动态轮廓模型(Snake),其能量表达式E=Eint+Eout.
该模型将轮廓曲线的一阶导数和二阶导数表示成内部能量Eint,以保证轮廓曲线在形变过程中很好地保持连续性和光滑性.同时通过外部能量的约束Eout,使得轮廓曲线向着目标移动.在传统的分割过程中,常采用经过高斯卷积的图像梯度平方作为外部能量.
由于传统的Snake模型仅在局部层面进行能量的最小化,未能对曲线整体形状进行约束,因此仅能获得局部约束下的结果.本文将先验知识融合到Snake模型中,建立先验Snake模型,以实现对轮廓的整体约束,获得全局约束下的最优解.
首先,使用归一化傅里叶描述子构建新的外部能量函数
| $ {E_{{\rm{out}}}} = {\left[ {{{\left| {\mathit{\boldsymbol{TV}}} \right|}^2} - {\mathit{\boldsymbol{b}}_0}} \right]^{\rm{T}}}\left[ {{{\left| {\mathit{\boldsymbol{TV}}} \right|}^2} - {\mathit{\boldsymbol{b}}_0}} \right]. $ |
式中:b0为目标轮廓傅里叶幅值的平方,V=[x(0)+jy(0), …, x(N-1)+jy(N-1)]T,离散傅里叶变换矩阵T通过以下公式计算获得:
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{{\rm{e}}^{\frac{{ - {\rm{j}}2{\rm{ \mathsf{ π} }} \cdot 0 \cdot 1}}{N}}}}&{{{\rm{e}}^{\frac{{ - {\rm{j}}2{\rm{ \mathsf{ π} }} \cdot 1 \cdot 1}}{N}}}}&{{{\rm{e}}^{\frac{{ - {\rm{j}}2{\rm{ \mathsf{ π} }} \cdot 2 \cdot 1}}{N}}}}& \cdots &{{{\rm{e}}^{\frac{{ - {\rm{j}}2{\rm{ \mathsf{ π} }} \cdot \left( {N - 1} \right) \cdot 1}}{N}}}}\\ {{{\rm{e}}^{\frac{{ - {\rm{j}}2{\rm{ \mathsf{ π} }} \cdot 0 \cdot 2}}{N}}}}&{{{\rm{e}}^{\frac{{ - {\rm{j}}2{\rm{ \mathsf{ π} }} \cdot 1 \cdot 2}}{N}}}}&{{{\rm{e}}^{\frac{{ - {\rm{j}}2{\rm{ \mathsf{ π} }} \cdot 2 \cdot 2}}{N}}}}& \cdots &{{{\rm{e}}^{\frac{{ - {\rm{j}}2{\rm{ \mathsf{ π} }} \cdot \left( {N - 1} \right) \cdot 2}}{N}}}}\\ {}&{}& \vdots &{}&{}\\ {{{\rm{e}}^{\frac{{ - {\rm{j}}2{\rm{ \mathsf{ π} }} \cdot 0 \cdot \left( {N - 1} \right)}}{N}}}}&{{{\rm{e}}^{\frac{{ - {\rm{j}}2{\rm{ \mathsf{ π} }} \cdot 1 \cdot \left( {N - 1} \right)}}{N}}}}&{{{\rm{e}}^{\frac{{ - {\rm{j}}2{\rm{ \mathsf{ π} }} \cdot 2 \cdot \left( {N - 1} \right)}}{N}}}}& \cdots &{{{\rm{e}}^{\frac{{ - {\rm{j}}2{\rm{ \mathsf{ π} }} \cdot \left( {N - 1} \right) \cdot \left( {N - 1} \right)}}{N}}}} \end{array}} \right]. $ |
改进后的离散化能量函数模型
| $ \begin{array}{l} E = \sum\limits_{n = 0}^{N - 1} {\left( {\alpha v_{\rm{s}}^2\left( n \right) + \beta v_{{\rm{ss}}}^2\left( n \right) + \gamma {e_{{\rm{img}}}}\left( n \right)} \right)} + \\ \;\;\;\;\;\varepsilon {\left[ {{{\left| {\mathit{\boldsymbol{TV}}} \right|}^2} - {\mathit{\boldsymbol{b}}_0}} \right]^{\rm{T}}}\left[ {{{\left| {\mathit{\boldsymbol{TV}}} \right|}^2} - {\mathit{\boldsymbol{b}}_0}} \right]. \end{array} $ |
式中:α为曲线一阶导能量项的权重,β为曲线二阶导能量项的权重,γ为图像能量项的权重,ε为外部能量项的权重.
为了方便表述,将外部能量表示为如下形式:
| $ \begin{array}{l} {E_{{\rm{out}}}} = {\left[ \mathit{\boldsymbol{W}} \right]^{\rm{T}}} \cdot \left[ \mathit{\boldsymbol{W}} \right] = \left[ {{w_1},{w_2}, \cdots ,{w_{N - 1}}} \right] \cdot \\ \;\;\;\;\;\;\;\;\;{\left[ {{w_1},{w_2}, \cdots ,{w_{N - 1}}} \right]^{\rm{T}}}. \end{array} $ |
式中向量W的具体表示形式为
| $ \mathit{\boldsymbol{W = }}{\left| {\mathit{\boldsymbol{TV}}} \right|^2} - {\mathit{\boldsymbol{b}}_0}, $ |
则外部能量对V的偏导数为
| $ \frac{{\partial {E_{{\rm{out}}}}}}{{\partial \mathit{\boldsymbol{V}}}} = 2\left[ {\begin{array}{*{20}{c}} {\frac{{\partial {w_1}}}{{\partial {v_0}}}}&{\frac{{\partial {w_2}}}{{\partial {v_0}}}}& \cdots &{\frac{{\partial {w_{N - 1}}}}{{\partial {v_0}}}}\\ {\frac{{\partial {w_1}}}{{\partial {v_1}}}}&{\frac{{\partial {w_2}}}{{\partial {v_1}}}}& \cdots &{\frac{{\partial {w_{N - 1}}}}{{\partial {v_1}}}}\\ {}&{}& \vdots &{}\\ {\frac{{\partial {w_1}}}{{\partial {v_{N - 1}}}}}&{\frac{{\partial {w_2}}}{{\partial {v_{N - 1}}}}}& \cdots &{\frac{{\partial {w_{N - 1}}}}{{\partial {v_{N - 1}}}}} \end{array}} \right] \cdot \left[ \begin{array}{l} {w_1}\\ {w_2}\\ \vdots \\ {w_{N - 1}} \end{array} \right] = 2 \cdot \mathit{\boldsymbol{J}} \cdot \mathit{\boldsymbol{W}}. $ |
实际使用时,主要使用外部能量分别在X和Y方向的偏导数,下面以JX和JY中的第一列为例,表示JX和JY的具体表达形式.雅克比矩阵中剩余的量可以按照同样的方式求解得到.
外部能量项由向量W组成,所以将w1元素分别对X中各个分量和Y中各个分量求偏导.其中,w1的表示形式如下:
| $ {w_1} = {\left[ {\begin{array}{*{20}{c}} {{x_0} - {\rm{j}}{y_0}}\\ {{x_1} - {\rm{j}}{y_1}}\\ \vdots \\ {{x_{N - 1}} - {\rm{j}}{y_{N - 1}}} \end{array}} \right]^{\rm{T}}} \cdot \left[ {\begin{array}{*{20}{c}} {{{\rm{e}}^{{\rm{j}}{\theta _0}}}}\\ {{{\rm{e}}^{{\rm{j}}{\theta _1}}}}\\ \vdots \\ {{{\rm{e}}^{{\rm{j}}{\theta _{N - 1}}}}} \end{array}} \right] \cdot {\left[ {\begin{array}{*{20}{c}} {{{\rm{e}}^{{\rm{ - j}}{\theta _0}}}}\\ {{{\rm{e}}^{{\rm{ - j}}{\theta _1}}}}\\ \vdots \\ {{{\rm{e}}^{{\rm{ - j}}{\theta _{N - 1}}}}} \end{array}} \right]^{\rm{T}}} \cdot \left[ {\begin{array}{*{20}{c}} {{x_0} + {\rm{j}}{y_0}}\\ {{x_1} + {\rm{j}}{y_1}}\\ \vdots \\ {{x_{N - 1}} + {\rm{j}}{y_{N - 1}}} \end{array}} \right], $ |
继而求解得到X方向雅克比矩阵和Y方向雅可比矩阵的第一列,如式(1)(2)所示:
| $ \left\{ {\begin{array}{*{20}{c}} {\partial {w_1}/\partial {x_0} = 2{x_0} + 2\left[ {{x_1}\cos \left( {{\theta _1} - {\theta _0}} \right) + {y_1}\sin \left( {{\theta _1} - {\theta _0}} \right)} \right] + \cdots + \\ 2\left[ {{x_{N - 1}}\cos \left( {{\theta _{N - 1}} - {\theta _0}} \right) + {y_{N - 1}}\sin \left( {{\theta _{N - 1}} - {\theta _0}} \right)} \right],}\\ {\partial {w_1}/\partial {x_0} = 2\left[ {{x_0}\cos \left( {{\theta _0} - {\theta _1}} \right) + {y_0}\sin \left( {{\theta _0} - {\theta _1}} \right)} \right] + 2{x_1} + \cdots + \\ 2\left[ {{x_{N - 1}}\cos \left( {{\theta _{N - 1}} - {\theta _1}} \right) + {y_{N - 1}}\sin \left( {{\theta _{N - 1}} - {\theta _1}} \right)} \right],}\\ \vdots \\ {\frac{{\partial {w_1}}}{{\partial {x_{N - 1}}}} = 2\left[ {{x_0}\cos \left( {{\theta _0} - {\theta _{N - 1}}} \right) + {y_0}\sin \left( {{\theta _0} - {\theta _{N - 1}}} \right)} \right] + \\ 2\left[ {{x_1}\cos \left( {{\theta _1} - {\theta _{N - 1}}} \right) + {y_1}\sin \left( {{\theta _1} - {\theta _{N - 1}}} \right)} \right] + \cdots + 2{x_{N - 1}},} \end{array}} \right. $ | (1) |
| $ \left\{ {\begin{array}{*{20}{c}} {\partial {w_1}/\partial {y_0} = 2{y_0} + 2\left[ {{y_1}\cos \left( {{\theta _0} - {\theta _1}} \right) + {x_1}\sin \left( {{\theta _0} - {\theta _1}} \right)} \right] + \cdots + \\ 2\left[ {{y_{N - 1}}\cos \left( {{\theta _0} - {\theta _{N - 1}}} \right) + {x_{N - 1}}\sin \left( {{\theta _0} - {\theta _{N - 1}}} \right)} \right],}\\ {\partial {w_1}/\partial {y_1} = 2\left[ {{y_0}\cos \left( {{\theta _1} - {\theta _0}} \right) + {x_0}\sin \left( {{\theta _1} - {\theta _0}} \right)} \right] + 2{y_1} + \cdots + \\ 2\left[ {{y_{N - 1}}\cos \left( {{\theta _1} - {\theta _{N - 1}}} \right) + {x_{N - 1}}\sin \left( {{\theta _1} - {\theta _{N - 1}}} \right)} \right],}\\ \vdots \\ {\partial {w_1}/\partial {y_{N - 1}} = 2\left[ {{y_0}\cos \left( {{\theta _{N - 1}} - {\theta _0}} \right) + {x_0}\sin \left( {{\theta _{N - 1}} - {\theta _0}} \right)} \right] + \\ 2\left[ {{y_1}\cos \left( {{\theta _{N - 1}} - {\theta _1}} \right) + {x_1}\sin \left( {{\theta _{N - 1}} - {\theta _1}} \right)} \right] + \cdots + 2{y_{N - 1}},} \end{array}} \right. $ | (2) |
根据Kass提出的模型,对能量函数进行最小化,得到满足最小化条件的特征方程
| $ \alpha {\mathit{\boldsymbol{X}}_{{\rm{ss}}}} + \beta {\mathit{\boldsymbol{X}}_{{\rm{ssss}}}} + \gamma \frac{{\partial {E_{{\mathop{\rm int}} }}}}{{\partial \mathit{\boldsymbol{X}}}} + \varepsilon \frac{{\partial {E_{{\rm{out}}}}}}{{\partial \mathit{\boldsymbol{X}}}} = 0, $ |
| $ \alpha {\mathit{\boldsymbol{Y}}_{{\rm{ss}}}} + \beta {\mathit{\boldsymbol{Y}}_{{\rm{ssss}}}} + \gamma \frac{{\partial {E_{{\mathop{\rm int}} }}}}{{\partial \mathit{\boldsymbol{Y}}}} + \varepsilon \frac{{\partial {E_{{\rm{out}}}}}}{{\partial \mathit{\boldsymbol{Y}}}} = 0. $ |
采取差分处理,可得
| $ \begin{array}{l} {\alpha _i}\left( {{\mathit{\boldsymbol{V}}_i} - {\mathit{\boldsymbol{V}}_{i - 1}}} \right) - {\alpha _{i + 1}}\left( {{\mathit{\boldsymbol{V}}_{i + 1}} - {\mathit{\boldsymbol{V}}_i}} \right) + {\beta _{i - 1}}\left[ {{\mathit{\boldsymbol{V}}_{i - 2}} - } \right.\\ \;\;\;\left. {2{\mathit{\boldsymbol{V}}_{i - 1}} + {\mathit{\boldsymbol{V}}_i}} \right] - 2{\beta _i}\left[ {{\mathit{\boldsymbol{V}}_{i - 1}} - 2{\mathit{\boldsymbol{V}}_i} + {\mathit{\boldsymbol{V}}_{i + 1}}} \right] + \\ \;\;\;{\beta _{i + 1}}\left[ {{\mathit{\boldsymbol{V}}_{i + 1}} - 2{\mathit{\boldsymbol{V}}_{i + 1}} + {\mathit{\boldsymbol{V}}_i}} \right] + \gamma \left( {{\mathit{\boldsymbol{f}}_X}\left( i \right),{\mathit{\boldsymbol{f}}_Y}\left( i \right)} \right) + \\ \;\;\;\varepsilon \left( {{\mathit{\boldsymbol{M}}_X}\left( i \right),{\mathit{\boldsymbol{M}}_Y}\left( i \right)} \right) = 0, \end{array} $ |
将其简写成
| $ \mathit{\boldsymbol{AX}} + \gamma {\mathit{\boldsymbol{f}}_X}\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{Y}}} \right) + \varepsilon {\mathit{\boldsymbol{M}}_X}\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{Y}}} \right) = 0, $ |
| $ \mathit{\boldsymbol{AX}} + \gamma {\mathit{\boldsymbol{f}}_Y}\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{Y}}} \right) + \varepsilon {\mathit{\boldsymbol{M}}_Y}\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{Y}}} \right) = 0. $ |
式中:A为一个五对角带状矩阵,fx和fy分别表示高斯卷积后的图像梯度在X和Y方向上的值,Mx和My为外部能量在X和Y方向上的偏导数向量,X和Y分别表示坐标的横坐标值组成的矢量和纵坐标值组成的矢量.
利用求解偏微分方程的Euler迭代方法,获得t时刻Xt和Yt的显示表达式
| $ \begin{array}{l} {\mathit{\boldsymbol{X}}_t} = {\left( {\mathit{\boldsymbol{A}} + \lambda \mathit{\boldsymbol{I}}} \right)^{ - 1}}\left( {\lambda {\mathit{\boldsymbol{X}}_{t - 1}} - {f_X}\left( {{\mathit{\boldsymbol{X}}_{t - 1}},{\mathit{\boldsymbol{Y}}_{t - 1}}} \right)} \right. - \\ \;\;\;\;\;\;\;\left. {\varepsilon {\mathit{\boldsymbol{M}}_X}\left( {{\mathit{\boldsymbol{X}}_{t - 1}},{\mathit{\boldsymbol{Y}}_{t - 1}}} \right)} \right), \end{array} $ |
| $ \begin{array}{l} {\mathit{\boldsymbol{Y}}_t} = {\left( {\mathit{\boldsymbol{A}} + \lambda \mathit{\boldsymbol{I}}} \right)^{ - 1}}\left( {\lambda {\mathit{\boldsymbol{Y}}_{t - 1}} - {f_Y}\left( {{\mathit{\boldsymbol{X}}_{t - 1}},{\mathit{\boldsymbol{Y}}_{t - 1}}} \right)} \right. - \\ \;\;\;\;\;\;\;\left. {\varepsilon {\mathit{\boldsymbol{M}}_Y}\left( {{\mathit{\boldsymbol{X}}_{t - 1}},{\mathit{\boldsymbol{Y}}_{t - 1}}} \right)} \right). \end{array} $ |
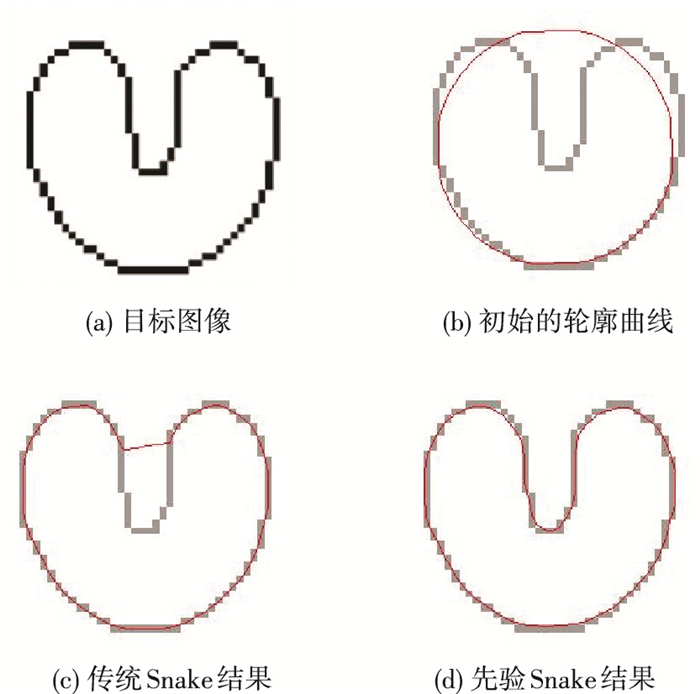
考虑到传统Snake算法对凹陷区域的不收敛,采用带有凹陷的U形轮廓对先验Snake算法进行测试.同时,也用实际超声图像进行算法验证,判断该算法在实际使用过程中的效果, 结果见图 1.
|
图 1 传统和先验Snake对U形轮廓的提取 Figure 1 Comparison between traditional and improved Snake methods in segmenting U shape |
在U形分割过程中,外部能量项权值取-3×10-12.从U形分割过程和结果可看出,传统Snake算法在凹陷区域不收敛,仅能达到局部最小值;而先验Snake算法克服了该缺陷,能够达到全局约束下的最优值,提高了分割精度.在同样参数条件下,先验Snake算法更快地收敛到了目标区域.
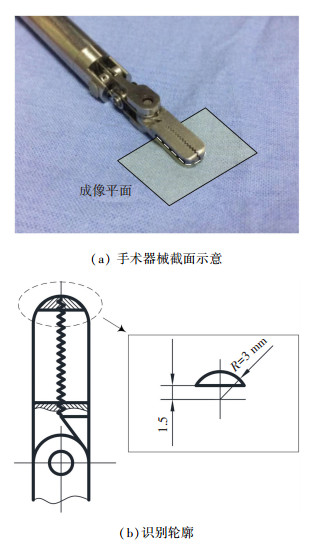
在本文的应用背景中,需要在超声图像中识别手术器械轮廓作为分割目标.则预先获知的手术器械截面轮廓将作为先验知识运用到分割轮廓中.手术器械截面轮廓如图 2所示.
|
图 2 超声图像分割目标 Figure 2 Segmentation target in ultrasound image |
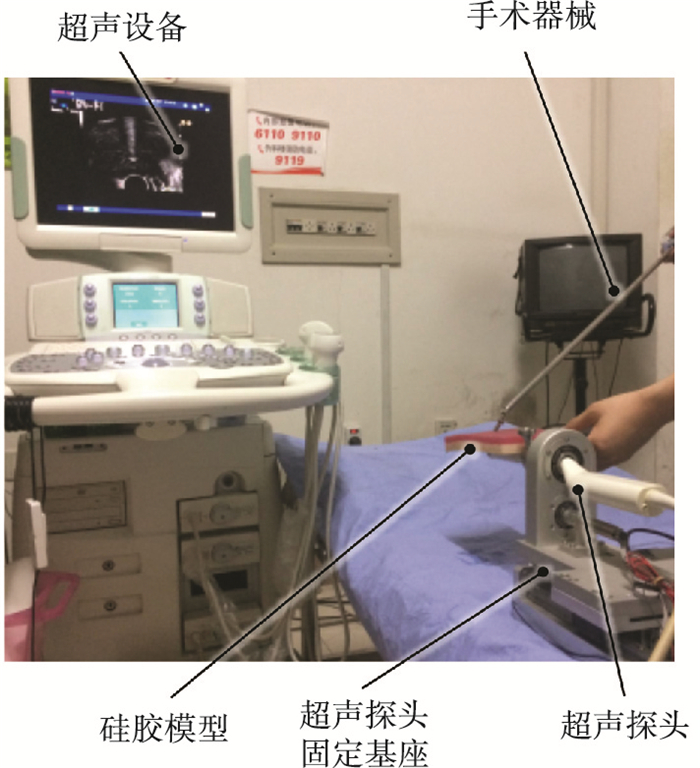
为了获得超声图像,搭建实验平台如图 3所示.采用的经直肠超声探头被固定在基座上,采像平面向上,隔着硅胶模型采集手术器械的图像.场景可以模拟当超声探头在直肠时,隔着直肠和前列腺采集手术器械图像的场景.
|
图 3 超声图像采像场景 Figure 3 Platform built up to acquire ultrasound image |
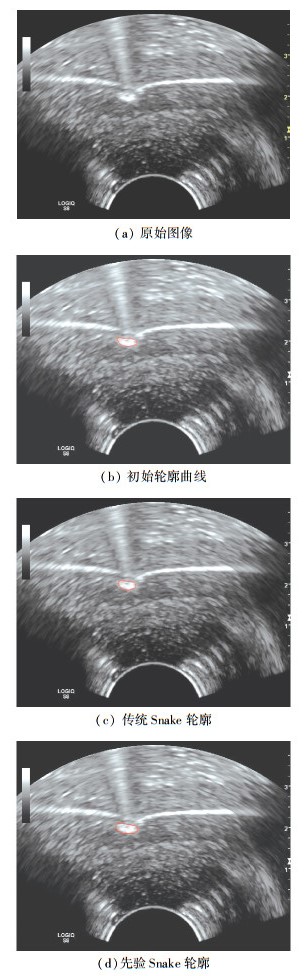
获得的原始超声图像见图 4(a).超声图像中微创器械的初始轮廓通过Hammer配准和减影获得,对该初始轮廓进行传统Snake算法和先验Snake算法迭代,可得图 4(c)(d)中的轮廓提取结果.
|
图 4 传统和先验Snake对微创器械的分割 Figure 4 Comparison between segmentation results using traditional Snake and improved Snake combined with prior knowledge |
在图 4中,超声图像微创器械的提取,外部能量项采用的权值系数为-10-10.通过对比传统Snake和先验Snake分割效果,发现先验Snake分割得到的轮廓更接近实际器械轮廓,获得全局约束下较优的解.
为了对分割效果进行量化评价,采用医生人工分割的轮廓作为“金标准”,将先验和传统Snake分割的轮廓与“金标准”进行对比.采用文献[14-15]中的方法,计算得到分割后轮廓与“黄金标准”轮廓的相似率εSI、重叠率εOF和误分割率εEF,如表 1所示.
| 表 1 传统Snake和先验Snake算法测度数值 Table 1 Index measurements of traditional Snake and improved Snake |
从图 1、4和表 1中发现:一方面,先验Snake算法克服了原始Snake算法对凹陷区域的不收敛缺陷,提高轮廓提取的准确性;另一方面,先验Snake算法能够融合先验知识,弥补了超声图像中斑点噪声引起的信息缺失,进而提高了超声图像中微创器械轮廓的提取精度.
4 结论1) 为了高精度地提取超声图像中的微器械轮廓,提出了一种全局约束下融合已知轮廓知识的参数活动轮廓超声图像分割方法,即先验Snake分割方法.该方法以归一化傅里叶描述子进行先验轮廓的描述,将该描述子定义的能量项作为Snake模型的外部能量项,实现了对轮廓曲线的全局约束.
2) 通过对能量方程进行雅克比求解、差分离散和Euler迭代,得到了曲线特征点的显示迭代式,避免了贪心搜索引发的陷入局部极小值情况.
3) 实验表明,先验Snake算法对凹陷区域具有收敛性,能够大幅度提高超声图像中微器械轮廓的提取精度.将其应用在微创机器人手术超声辅助成像系统中,能够极大地提高超声探头对微器械的追踪精度.
| [1] |
MOHARERI O, RAMEZANI M, ADEBAR T K, et al. Automatic localization of the da Vinci surgical instrument tips in 3-D transrectal ultrasound[J].
IEEE Transactions on Biomedical Engineering, 2013, 60(9): 2663-2672.
DOI: 10.1109/TBME.2013.2262499 |
| [2] |
YUAN Jianlin. The study of laparoscopic radical prostatectomy vs. robot-assisted laparoscopic prostatectomy on sexual function[J].
Translational Andrology and Urology, 2016, 5(Suppl 1): AB052-AB052.
DOI: 10.21037/tau.2016.s052 |
| [3] |
UKIMURA O, MAGI-GALLUZZI C, GILL I S. Real-time transrectal ultrasound guidance during laparoscopic radical prostatectomy: impact on surgical margins[J].
Journal of Urology, 2006, 175(4): 1304-1310.
DOI: 10.1016/S0022-5347(05)00688-9 |
| [4] |
ADEBAR T K, MOHARERI O, SALCUDEAN S E. Instrument-based calibration and remote control of intraoperative ultrasound for robot-assisted surgery[C]//IEEE Ras & Embs International Conference on Biomedical Robotics and Biomechatronics. Washington: IEEE Computer Society, 2012: 38-43. DOI: 10.1109/BioRob.2012.6290896.
|
| [5] |
周振环, 王安明, 王京阳, 等.
医学图像分割与配准[M]. 西安: 西安电子科技大学出版社, 2007: 136-204.
ZHOU Zhenhuan, WANG Anming, WANG Jingyang, et al. Medical image segmentation and registration[M]. Xidian University Press: 2007: 136-204. |
| [6] |
OHTSU N. A threshold selection method from gray-level histograms[J].
IEEE Transactions on Systems Man & Cybernetics, 2007, 9(1): 62-66.
DOI: 10.1109/TSMC.1979.4310076 |
| [7] |
兰红, 闵乐泉. 多阈值优化交互式分割算法及其在医学图像中的应用[J].
计算机应用, 2013, 33(5): 1435-1431.
LAN Hong, MIN Lequan. Interactive segmentation algorithm optimized by multi-threshold with application in medical images[J]. Journal of Computer Applications, 2013, 33(5): 1435-1431. |
| [8] |
TATIRAJU S, MEHTA A. Image segmentation using k-means clustering, EM and normalized cuts[J].
University of California-Irvine, 2008(1): 1-7.
|
| [9] |
CARNEIRO G, NASCIMENTO J C, FREITAS A. The segmentation of the left ventricle of the heart from ultrasound data using deep learning architectures and derivative-based search methods[J].
IEEE Transactions on Image Processing, 2012, 21(3): 968-982.
DOI: 10.1109/TIP.2011.2169273 |
| [10] |
MARSOUSI M, ALIREZAIE J, AHMADIAN A, et al. Segmenting echocardiography images using B-Spline snake and active ellipse model[C]//Engineering in Medicine and Biology Society. Piscataway: IEEE, 2010: 3125-3128. DOI: 10.1109/IEMBS.2010.5626094.
|
| [11] |
KASS M, WITKIN A P, TERZOPOULOS D. Snake: active contour models[J].
International Journal of Computer Vision, 1988, 1(4): 321-331.
DOI: 10.1007/BF00133570 |
| [12] |
王小林, 刘宏申, 秦锋. 基于snake模型的目标检测[J].
华中科技大学学报(自然科学版), 2008, 36(1): 75-77.
WANG Xiaolin, LIU Hongshen, QIN Feng. Finding objects with snake model[J]. Journal of Huazhong University of Science & Technology, 2008, 36(1): 75-77. DOI: 10.3321/j.issn:1671-4512.2008.01.021 |
| [13] |
王涛, 刘文印, 孙家广, 等. 傅里叶描述子识别物体的形状[J].
计算机研究与发展, 2002, 39(12): 1714-1719.
WANG Tao, LIU Wenyin, SUN Jiaguang, et al. Using Fourier descriptors to recognize object's shape[J]. Journal of Computer Research & Development, 2002, 39(12): 1714-1719. |
| [14] |
倪雅樱. 基于Snake模型的医学图像分割技术[D]. 南京: 南京航空航天大学, 2008: 53-54.
NI Yaying. The technology of medical image segmentation based on snake model[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008: 53-54. http://d.wanfangdata.com.cn/Periodical/shswyxgc200703010 |
| [15] |
ANBEEK P, VINCKEN K L, van OSCH M J, et al. Probabilistic segmentation of white matter lesions in MR imaging[J].
Neuroimage, 2004, 21(3): 1037-1044.
DOI: 10.1016/j.neuroimage.2003.10.012 |
 2018, Vol. 50
2018, Vol. 50


